HEAT TRANSFER CONDUCTION HEAT TRANSFER gjv Recap Heat















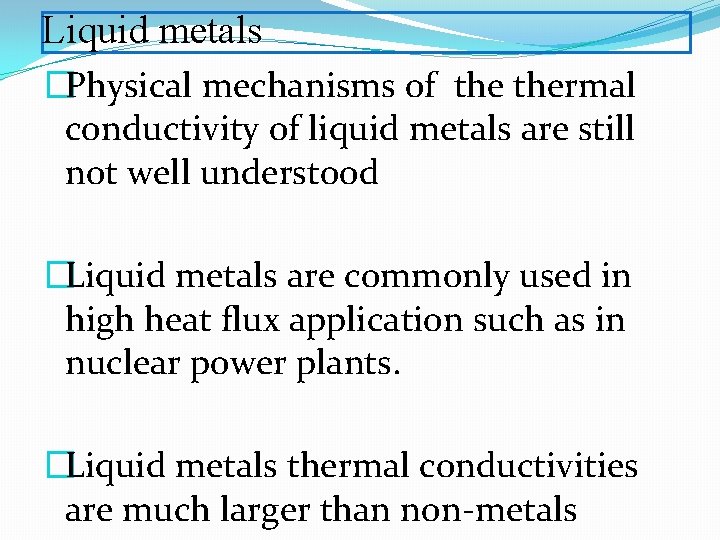














![Example �What is the critical radius of insulation for asbestos [k=0. 17 W/mo. C] Example �What is the critical radius of insulation for asbestos [k=0. 17 W/mo. C]](https://slidetodoc.com/presentation_image/324d2f3cc99bfdda31f7ee1fb49171c5/image-38.jpg)
- Slides: 38

HEAT TRANSFER CONDUCTION HEAT TRANSFER gjv

Recap �Heat flows from hot to cold regions �Ease of movement of electrons in metals the reason for greater distribution of energy compared to other substances and explains the relationship between thermal and electrical conductivities �Conducting medium necessary for conduction

Basic law of conduction �Temperature gradient leads to energy transfer �Heat transfer per unit area (heat flux) proportional to normal temperature gradient

Fourier’s Law of heat conduction � �For steady state one dimensional heat flow, the rate of heat flow in the x direction normal to the surface area, is directly proportional to the temperature gradient, the area of flow and inversely proportional to the distance.

Fourier’s Law �Key features of the law �Not an expression that may be derived from first principle �A generalization based on experimental evidence �Defines the important material property of thermal conductivity

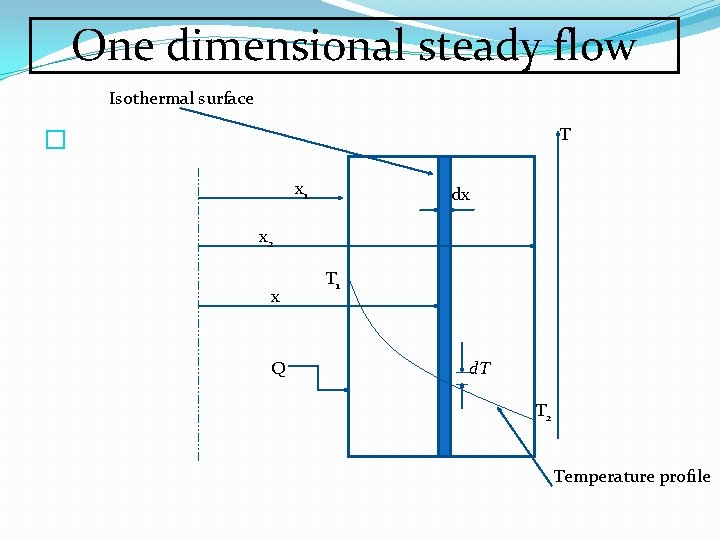
One dimensional steady flow Isothermal surface T � x 1 dx x 2 x Q T 1 d. T T 2 Temperature profile

Assumptions �Uniform temperatures over the surface perpendicular to x which is the direction of heat conduction ( isothermal surface) �Steady flow ( Temperature does not vary with time) �Rate of heat flow constant �Consider an element of thickness dx with surfaces at temperature of T and T+d. T

�From Fourier’s Law: Thermal conductivity of material

Thermal Conductivity �k, though not a function of temperature gradient, is a function of temperature and from experimental data:

Thermal Conductivity �

Thermal Conductivity �For a nonlinear k the mean value is given by: Thermal conductivities of metals are usually very high Non-metallic solids and liquids lower

The Solid State �Modern view of solids highlights free electrons and atomic lattice structure �Thermal energy determined by Lattice vibrations which are additive: �k = ke+kl but we know that � ke= 1/ρe electrical resisticity �For pure metals with low ρe ke>>kl

The Solid State �Hence contribution of kl to k is negligible �For alloys where ρe is large contribution of kl to k is no longer negligible �For non-metals, k is determined primarily by kl and depends on the frequency of interaction between atoms of the lattice �Chrystalline, well ordered substances such as diamond & quartz have high k values compared with amorphous substances (glass)

The fluid state �Larger intermolecular spacing and greater random motion lead to lower thermal energy transport �Thermal conductivity of gases and liquids more similar than solids �Kinetic theory of gases gives a good account of their thermal conductivities �Thermal conductivity of gases is directly proportional to the number of particles per unit volume, mean molecular speed and mean free path (Average distance travelled by a molecule before a collision)

Fluids �k α ncλ �Thermal conductivities of gases increase with increasing temperature and decreasing molecular weight since c increases accordingly �Thermal conductivities of gases are independent of pressure since n & λ are directly and indirectly proportional to gas pressure respectively

Thermal conductivity �Conductivity of alloys less than the pure metals �Gases have very low conductivities and for ideal gases k is proportional to mean molecular velocity, mean free path and molar heat capacity
Liquid metals �Physical mechanisms of thermal conductivity of liquid metals are still not well understood �Liquid metals are commonly used in high heat flux application such as in nuclear power plants. �Liquid metals thermal conductivities are much larger than non-metals

Temperature dependence of conductivity �Thermal insulation comprise low conductivity materials which when combined achieve even lower system thermal conductivity �Fiber, powder and flake type insulation have solid material finely dispersed in air spaces �The nature and volumetric fraction of the solid to void ratio characterizes thermal conductivity of the insulation

Insulation �Cellular insulation – hollow spaces or small voids are sealed from each other and formed by fusion or bonding of solid material in a rigid matrix � Foam systems (plastic or glass) �Reflective insulation – thin sheets of high reflectivity foil spaced to reflect radiant energy �Evacuation of air from voids reduce effective thermal conductivity

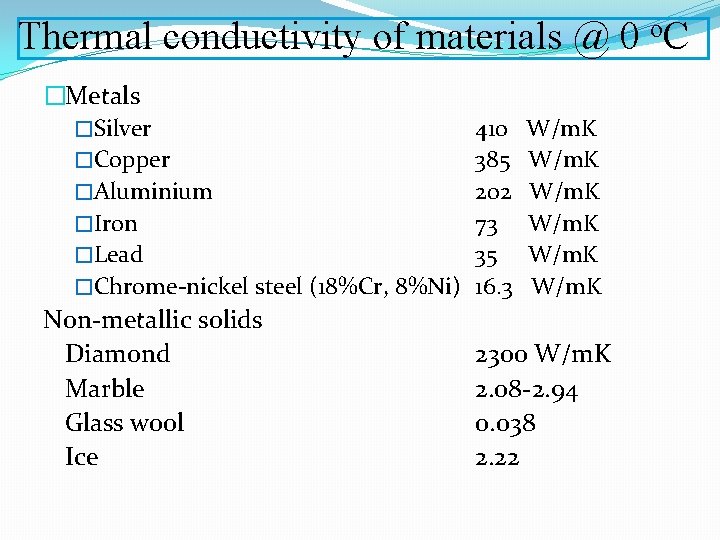
Thermal conductivity of materials @ 0 o. C �Metals �Silver �Copper �Aluminium �Iron �Lead �Chrome-nickel steel (18%Cr, 8%Ni) Non-metallic solids Diamond Marble Glass wool Ice 410 385 202 73 35 16. 3 W/m. K 2300 W/m. K 2. 08 -2. 94 0. 038 2. 22

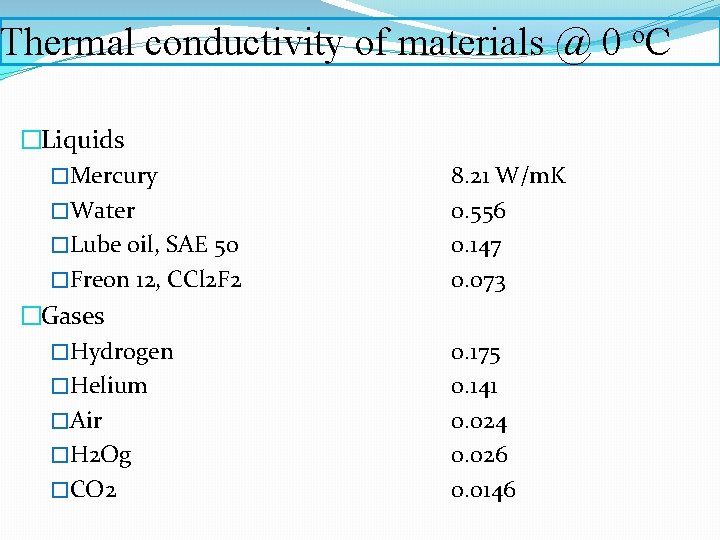
Thermal conductivity of materials @ 0 o. C �Liquids �Mercury �Water �Lube oil, SAE 50 �Freon 12, CCl 2 F 2 �Gases �Hydrogen �Helium �Air �H 2 Og �CO 2 8. 21 W/m. K 0. 556 0. 147 0. 073 0. 175 0. 141 0. 024 0. 026 0. 0146

Example �One face of a copper plate 3. 0 cm thick is maintained at 400. 0 o. C and the other face is kept at 100. 0 o. C. How much heat is transferred through the plate? �KCu = 370. 0 W/m. K @ 250. 0 o. C �Estimate the heat loss per m 2 through a brick wall 0. 5 m thick when the inner surface is at 400. 0 K and the outside surface is at 300. 0 K. �Kbrik = 0. 7 W/m. K @ 350. 0 o. C

Thermo physical properties �Important properties for heat transfer calculations: �Kinematic viscosity, ν (m 2/s) �Density, ρ (kg/m 3) �Heat capacity, cp, cv (J/m 3 K) �Thermal diffusivity, α (m 2/s)

Thermal diffusivity �The ability to conduct thermal energy relative to the ability to store it: �Materials with large α respond quickly to changes in their thermal environment �Accuracy of engineering calculations depend on the accuracy of determining thermo-physical properties

Example �Use tables to calculate α for the following: �Pure Aluminium @ 300 K $ 700 K �Silicon Carbide @ 1000 K �Parafin @ 300 K

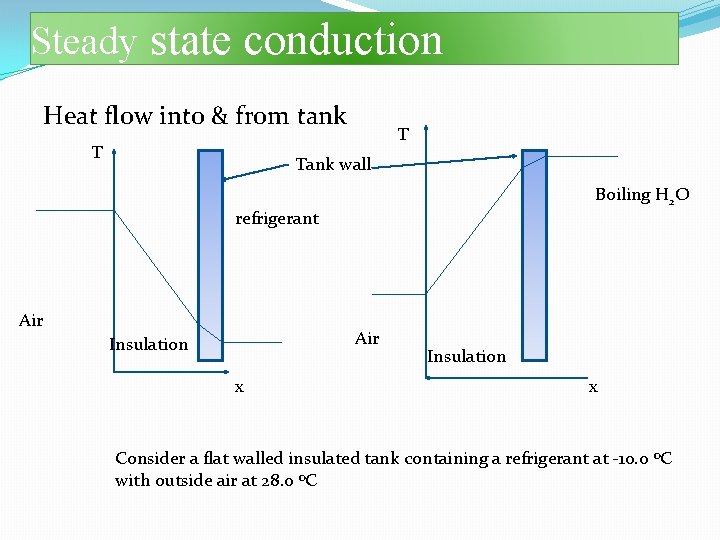
Steady state conduction Heat flow into & from tank T T Tank wall Boiling H 2 O refrigerant Air Insulation x Consider a flat walled insulated tank containing a refrigerant at -10. 0 o. C with outside air at 28. 0 o. C

Steady flow conduction �For x distance from the hot side: Thermal resistance

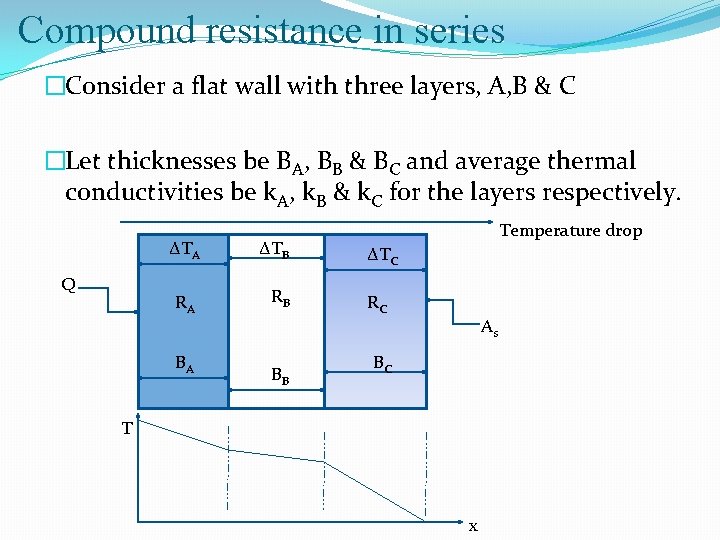
Compound resistance in series �Consider a flat wall with three layers, A, B & C �Let thicknesses be BA, BB & BC and average thermal conductivities be k. A, k. B & k. C for the layers respectively. ∆TA Q RA BA ∆TB RB BB Temperature drop ∆TC RC As BC T x

Compound resistance in series �

Compound resistance in series

Example �An exterior wall of a house consists of a 4. 0 cm of common brick [k=0. 7 W m-1 o. C-1] and a 1. 5 cm layer of gypsum plaster [k =0. 48 W m-1 o. C-1]. What thickness of loosely packed rock-wool [k=0. 065 W m-1 o. C-1] insulation should be added to reduce the heat loss (or gain) through the wall by 80. 0 %?

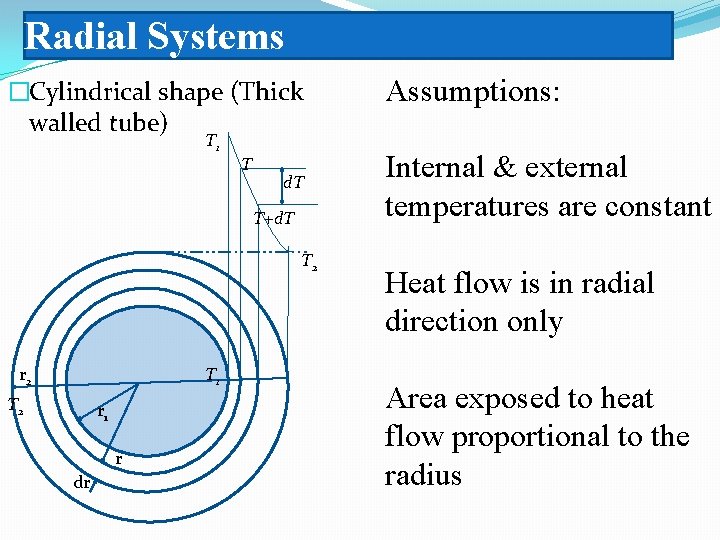
Radial Systems �Cylindrical shape (Thick walled tube) T 1 T d. T T+d. T T 2 r 2 T 1 T 2 r 1 r dr Assumptions: Internal & external temperatures are constant Heat flow is in radial direction only Area exposed to heat flow proportional to the radius

Thick walled tube

Thick walled tube The thermal resistance would then be: For multiple cylindrical layers:

Example �A tube of 60. 0 mm OD is insulated with a 50. 0 mm layer of silica foam [k=0. 055 W/mo. C] and a 40. 0 mm layer of cork [k=0. 05 W/mo. C]. Calculate the heat loss per unit length of pipe given that the temperature at the inner surface of the pipe is 150. 0 o. C while the outer surface of the cork is kept at 30. 0 o. C.

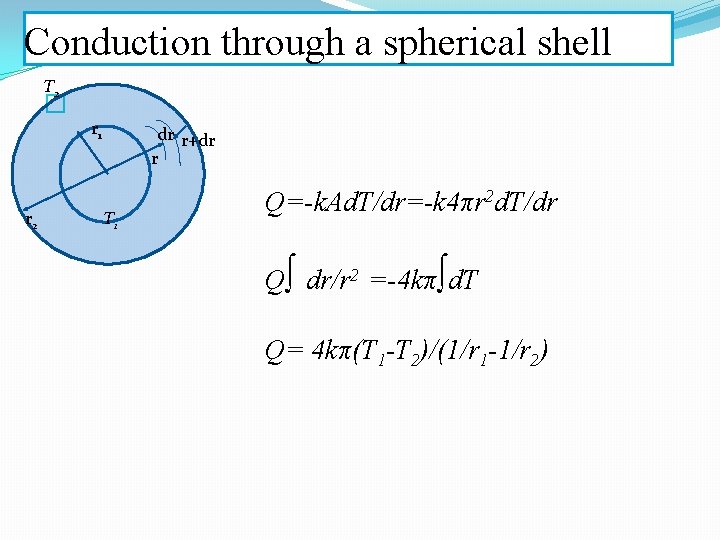
Conduction through a spherical shell T 2 � r 1 r 2 dr r+dr r T 1 Q=-k. Ad. T/dr=-k 4πr 2 d. T/dr Q∫ dr/r 2 =-4 kπ∫d. T Q= 4 kπ(T 1 -T 2)/(1/r 1 -1/r 2)

Critical Thickness of insulation �For a pipe covered with a layer of insulating material Inner temp of insulation fixed at T 1 outer temp at T 2 r 1 T 1 r 2
![Example What is the critical radius of insulation for asbestos k0 17 Wmo C Example �What is the critical radius of insulation for asbestos [k=0. 17 W/mo. C]](https://slidetodoc.com/presentation_image/324d2f3cc99bfdda31f7ee1fb49171c5/image-38.jpg)
Example �What is the critical radius of insulation for asbestos [k=0. 17 W/mo. C] insulation on a pipe in a room at ambient temperature of 20. 0 o. C, where h=3. 0 W/m 2 o. C and what would be the heat loss from a 5. o cm diameter pipe kept at 200. 0 o. C when covered with this critical radius of insulation as well as without?