Heat Conduction in Solids Overview of Heat Conduction

Heat Conduction in Solids

Overview of Heat Conduction in Solids • Many MEMS devices are actuated thermally. Key issues involve : – The amount of heat required to invoke the desired action. – The time required for initiating and terminating the action. – The associated thermal stresses and strain induced in the device. – The possible damage to sensitive components of the device due to heating.

General Principle of Heat Conduction • Consider conduction in a slab of thickness d and temperatures Ta and Tb on the left- and righthand side, respectively (Ta > Tb). • The amount of heat Q flowing in a time t is • k is thermal conductivity of the solid expressed in units of W/m-°C in SI system.

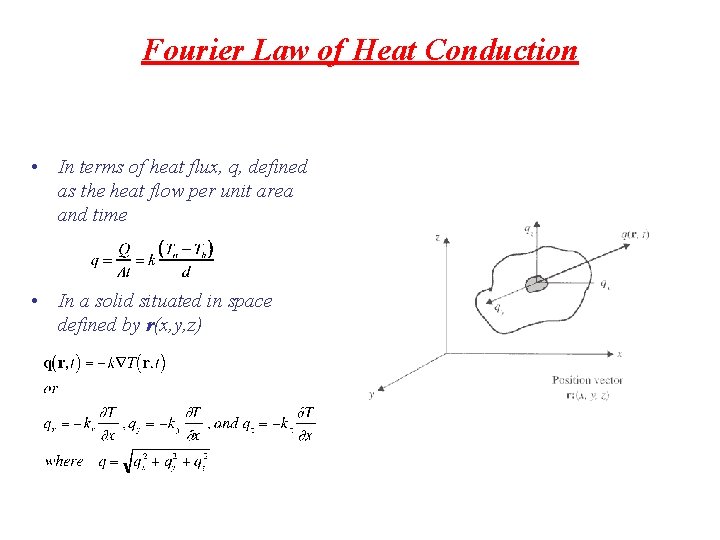
Fourier Law of Heat Conduction • In terms of heat flux, q, defined as the heat flow per unit area and time • In a solid situated in space defined by r(x, y, z)

The Heat Conduction Equation • When a solid is subject to heat input source, or dissipates heat to the surrounding medium at a rate Q(r, t) per unit volume, the temperature field T(r, t) may be obtained using the heat conduction equation • The thermal diffusivity is measured in units of m 2/s in SI system. is a measure of how fast the solid can conduct heat and is given by c is the specific heat of the solid • A common heat source in MEMS is electric resistance, R, in which a current, i, generates a power P given by

Newton’s Cooling Law • Heat transmission in solids is via conduction, whereas in fluids convection is the mode of heat transfer. • For the fluid shown the heat flux q is expressed as • The constant h has several names one of which is “transfer coefficient”.

Important Relations in Fluids • h is normally embedded in “Nusselt number”, Nu, via where L is a characteristic length • The following relations are normally used to determine Nu the parameters b g and d in the expressions for Nu, are experimentally determined parameters) – Reynold’s number, Re – Prandtl number, PR – Grashoff number, Gr • In the above relations cp is the specific heat of fluids under constant pressure, b is the volumetric coefficient of thermal expansion, and Dt is the duration. • For most convective heat transfer in fluids where for a given fluid the parameter f is determined experimentally.

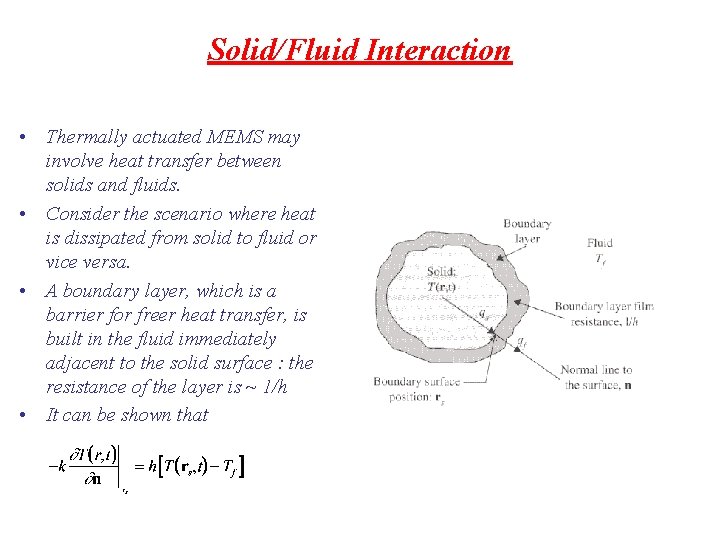
Solid/Fluid Interaction • Thermally actuated MEMS may involve heat transfer between solids and fluids. • Consider the scenario where heat is dissipated from solid to fluid or vice versa. • A boundary layer, which is a barrier for freer heat transfer, is built in the fluid immediately adjacent to the solid surface : the resistance of the layer is ~ 1/h • It can be shown that

The Boundary Conditions (BCs) : i) Prescribed Surface Temperature • The heat conduction equation is used to determine T(r, t). For design purposes it is necessary to determine locations in the solid with maximum temperature as well as thermal stress distribution • In the prescribed surface temperature BC • The function F(t) can be a constant in special cases.

ii) Prescribed Heat Flux at the Boundary • This is the BC in which the flux qin entering and qout leaving the solid are specified. These heat fluxes can be expressed by the Fourier law. • The signs in the equations are determined using the table.

iii) Convective Boundary Conditions • In this BC the solid boundary is in contact with fluid at temperature Tf • One notes that is equivalent to the BC in (i) , whereas the case of h = 0 leads to the insulated boundary condition

Heat Conduction in Multilayered Thin Films • MEMS structure involves stacks of several thin films. This necessitates heat conduction analysis through the films. • The temperature field in the ith film, Ti • Prescribed initial conditions in xi ≤ xi+1 at t = 0, and prescribed BCs at x = 0 and x = xi+1 for t > 0. • The continuity conditions imply

Thermal Conductivity of Thin Films • A simple model based on molecular heat transfer gives k in thin films as • A more refined theory gives for the effective k, keff , in a thin film of thickness H (kb is thermal conductivity of the bulk material of the film

Heat Conduction Equation for Thin Films • The lag time between heat flow and temperature gradient is insignificant in bulk materials, but it must be accounted for in thin films. • This results in a modified heat conduction equation in thin films • The last term represents the velocity of heat transmission in solids: it is in the form of wave propagation of T(r, t) and is called thermal wave propagation in the solid. This term is insignificant when H >> lo, where lo is the average mean free path. • t is the “relaxation time”, which is the average time that a carrier, e. g. , a phonon, travels between collisions

Thermomechanics

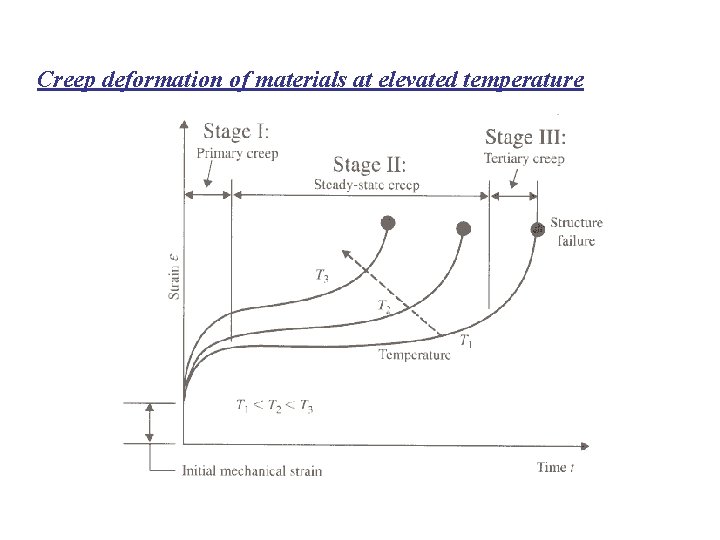
Introduction • Many MEMS are fabricated at elevated temperature, such as in bonding or oxidation, or are operated at elevated temperatures. • Thermal effects are an important factor in the design and packaging in MEMS. • There are generally three serious effects on MEMS exposed to elevated temperatures – Thermal effects on mechanical strength of materials – Creep deformation – Thermal stresses

Variation of material properties with temperature

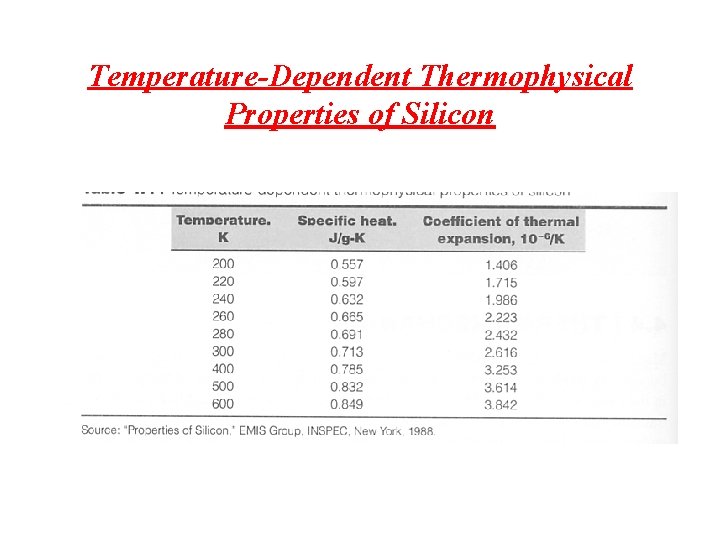
Temperature-Dependent Thermophysical Properties of Silicon

Creep deformation of materials at elevated temperature

Thermal Stresses • A bar with fixed ends – The temperature rise DT = T 2 T 1 – The parameters s. T and e. T are temperature stress and strain, respectively. – The thermal expansivity of the material is .

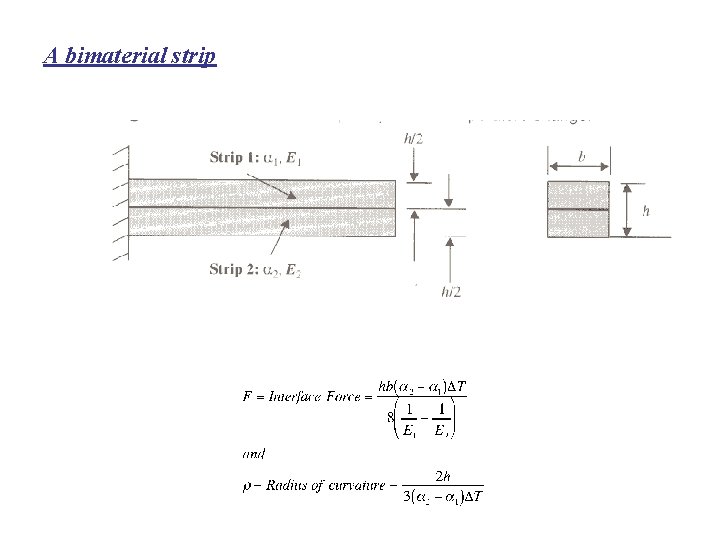
A bimaterial strip

Designation of stress components in a solid

Thermal stresses in thin plates (diaphragm) with DT through the thickness

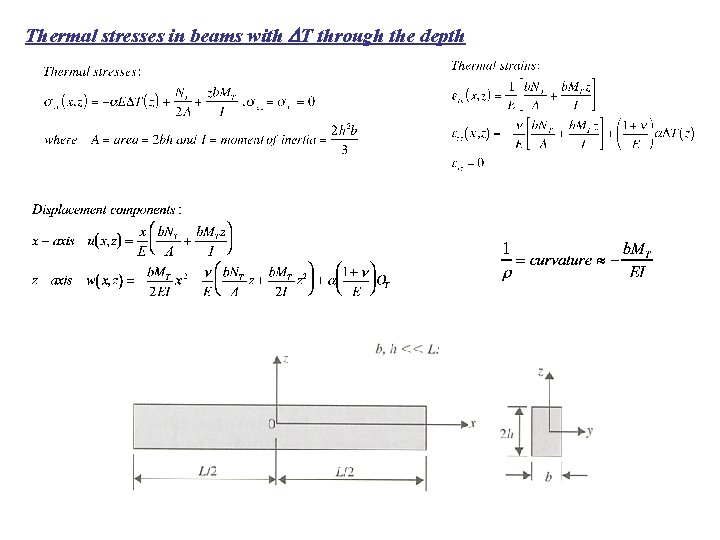
Thermal stresses in beams with DT through the depth