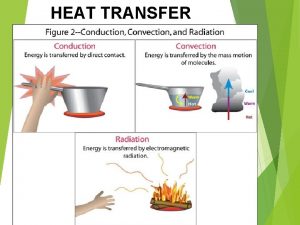
HEAT TRANSFER Transient Conduction 1 Transient Conduction Any

HEAT TRANSFER Transient Conduction 1

Transient Conduction Any body subjected to a sudden change in environment experiences a time lapse before reaching equilibrium or steady state. Prior to the equilibrium the process is in unsteady state or transient For heat transfer this amounts to the change in the internal energy of the body. 2

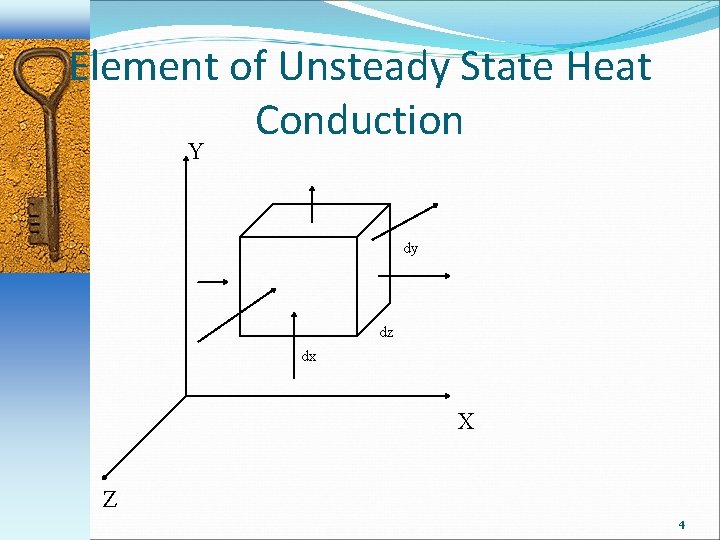
Transient Conduction Unsteady state conduction is responsible for the temperature distribution when a body is heated or cooled steadily from a starting temperature. Consider a 3 D element of a body with dimensions, dx, dy, and dz, at temperature T at point (x. y. z) and T+d. T at (x+dx, y+dy, z+dz) Assuming constant thermal conductivity and that no heat is generated in the element 3

Element of Unsteady State Heat Conduction Y dy dz dx X Z 4

Heat conduction through the element is: . A 5

Transient Conduction The rate of change of the element’s heat content is minus the rate of increase of heat flow from (x, y, z) to (x+dx, y+dy, z+dz) 6

Transient Conduction The rate of increase of heat content is also equal to the product of the heat capacity and rate of temperature increase, hence: 7

Laplace transform of temperature with respect to time may be used to solve this partial differential equation. From the basic differential equation for the xdirection: 8

t=0 T>0, T=T’, when x=0 T>0, δT/δx=0, when x=L Which after substitution and rearrangement assuming the temperature everywhere is constant initially, gives: 9

This equation may also written as: This series converges rapidly so by substituting the relevant values the equation may be solved. 10

Example How long will it take the distant face of a 0. 45 m thick brick wall (α=0. 0043 cm 2 s-1) to rise from 295. 0 K to 375. 0 K if the temperature of the entire wall was initially held constant at 295. 0 K before suddenly increasing and holding the near face to 900. 0 K. Assume perpendicular heat flow and perfect insulation at the first face. 11

The temperature at any distance x from the near face at time t is given by: The temperature at the distant face (x=0) is therefore given by: If the initial temperature is zero everywhere, then: 12

Approximating to the first term only gives: 364 t-0. 5 = 1. 3 t= 70840 s = 19. 7 h 13

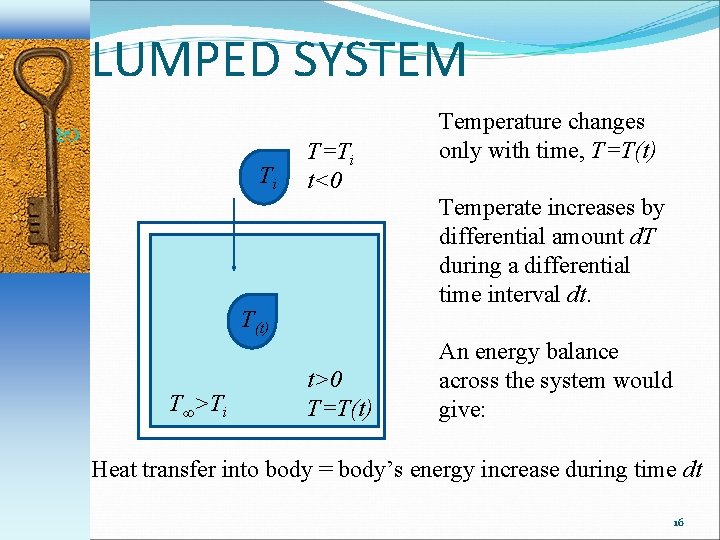
LUMPED HEAT CAPACITY SYSTEM The temperature of a body is not always uniform throughout Some bodies may behave like a “lump” with uniform temperature throughout the interior This ideal system allows for heat transfer based on the Lumped System Analysis A metal ball taken from a furnace at 85 o. C will undergo a temperature change with time but not position. 14

LUMPED SYSTEM But a large turkey taken out before time will be well done on the outside but not in the centre This would not be a good case for the lumped system analysis For a body of arbitrary shape and mass m, volume v surface area A specific heat capacity CP initially at uniform temperature Ti and density ρ placed in a liquid at temperature T∞ and heat transfer coefficient h when time t=0 heat transfer will take place if T∞>Ti 15

LUMPED SYSTEM Ti T=Ti t<0 Temperate increases by differential amount d. T during a differential time interval dt. T(t) T∞>Ti Temperature changes only with time, T=T(t) t>0 T=T(t) An energy balance across the system would give: Heat transfer into body = body’s energy increase during time dt 16

LUMPED SYSTEM Where temperature difference, d. T=d(T-T∞) me i t the o e in y t m r d T e o t e b e r d e ratu h o t t r d o mpe e f s d U ire te e u req h som c rea 17

LUMPED SYSTEM Used to determine the time required for the body to reach some temperature T Taking the exponential of both sides and rearranging t n a t s n me co i 1/b=t 18

LUMPED SYSTEM T(t) T∞ T 1 b 3 b 2 The temperature of the body approaches the ambient temperature exponentially b 1 b 3>b 2>b 1 Large b value means shorter time to reach ambient temperature since b is proportional to the surface area but inversely proportional to the mass and specific heat of the body 19

LUMPED SYSTEM Newton’s law of cooling may be used to calculate the rate of convection heat transfer if the temperature, T(t) at time, t is known Total heat transfer between t=0 and t is the change in energy content of the body Heat transfer reaches upper limit when the body reaches the ambient temperature, T∞ 20

CRITERIA FOR LUMPED SYSTEM This the simplest and most consistent method for solving transient heat transfer problems but its accuracy depend on the prevailing conditions For steady state conductance through a solid wall where one surface is maintained at Ts, 1 while the other is exposed to a fluid at T∞<Ts, 1 T∞<Ts, 2 <Ts, 1 Under steady state conditions 21

CRITERIA FOR LUMPED SYSTEM Dimensionless Biot number plays a fundamental role in solving conduction problems involving surface convecton 22

CRITERIA FOR LUMPED SYSTEM Measurement of the temperature drop of a solid relative to the temperature difference between solid and fluid surface Bi<<1 uniform temperature difference across a solid at any time during the transient process due to small resistance to heat conduction The smaller the Bi number the more accurate the lumped system analysis. Generally lumped system analysis is applicable if Bi<0. 1 23

Example A metal ball (ρ=7800 kgm-3, c. P =0. 46 k. Jkg-1 o. C-1 & k=35. 0 Wm-1 o. C-1) with a diameter of 5. 0 cm and initially kept at a uniform temperature of 450. 0 o. C is suddenly subjected to a constant temperature of 100 o. C in a controlled environment. If the convection heat transfer coefficient, h= 10. 0 Wm-2 o. C, calculate the time required for the ball to attain a temperature of 150. 0 o. C. {Because of the low h value the lumped capacity method should apply}: Checking: Bi = hlc/k=h(V/A)/k=10*4/3*π*(0. 025)3 = 0. 00714 < 0. 1 4π *(0. 025)2*35 24

25

Example 2 An egg which approximates to a sphere 5. 0 cm in diameter and initially held at 5. 0 o. C is dropped into boiling water at 95. 0 o. C. If the convection heat transfer coefficient, h=1200. 0 Wm-2 o. C-1 how long will it take for the centre of the egg to attain a temperature of 70. 0 o. C? 26

Questions & Answers 27