Navrhovanie experimentov DOE Design of Experiment 1 as

Navrhovanie experimentov – DOE (Design of Experiment) 1. časť Postup pri návrhu experimentu

Obsah • • • • • • • Experiment Predpoklady experimentu Postup pri návrhu experimentu Ciele experimentu Výber vstupných a výstupných charakteristík Nastavenie spojitých faktorov Kódovanie úrovní spojitých faktorov Model pre spojité faktory Množstvo dát Dvojúrovňový úplný faktorový plán experimentu Trojúrovňový úplný faktorový plán experimentu Matica pre model Replikácie a znáhodnenie Počet replikácií Jednorozmerná lineárna regresná analýza – model Jednorozmerná lineárna regresná analýza – metóda najmenších štvorcov Jednorozmerná lineárna regresná analýza – ANOVA Jednorozmerná lineárna regresná analýza – odhady b 0 a b 1 Jednorozmerná lineárna regresná analýza – t-test Jednorozmerná lineárna regresná analýza – koeficient determinácie Jednorozmerná lineárna regresná analýza – predikcia Jednorozmerná lineárna regresná analýza – závislosť šírky konfidenčného a predikčného intervalu od n Jednorozmerná lineárna regresná analýza – geometrický význam konfidenčných a predikčných intervalov Jednorozmerná lineárna regresná analýza – Lack of Fit Error Jednorozmerná lineárna regresná analýza – analýza rezíduí Viacrozmerná polynomická regresná analýza – model Viacrozmerná polynomická regresná analýza – interakcia Viacrozmerná polynomická regresná analýza – metóda najmenších štvorcov, množstvo dát 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 • • • Viacrozmerná polynomická regresná analýza – ANOVA pre celý model Viacrozmerná polynomická regresná analýza – odhady efektov, testy významnosti Viacrozmerná polynomická regresná analýza – upravený koeficient determinácie Príklad Použitá a doporučená literatúra a softvér 31 32 33 34 50 18 19 20 21 22 23 24 25 26 27 28 29 30 Postup pri návrhu experimentu 2

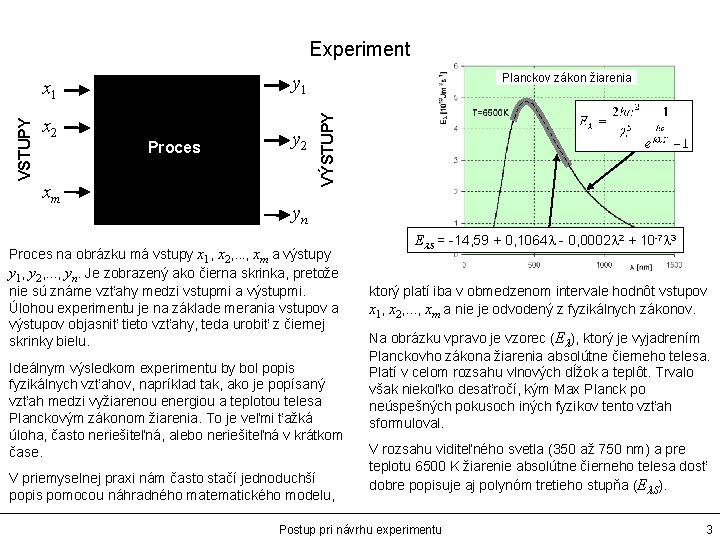
Experiment y 1 x 2 xm Proces y 2 Planckov zákon žiarenia VÝSTUPY VSTUPY x 1 yn Proces na obrázku má vstupy x 1, x 2, . . . , xm a výstupy y 1, y 2, . . . , yn. Je zobrazený ako čierna skrinka, pretože nie sú známe vzťahy medzi vstupmi a výstupmi. Úlohou experimentu je na základe merania vstupov a výstupov objasniť tieto vzťahy, teda urobiť z čiernej skrinky bielu. Ideálnym výsledkom experimentu by bol popis fyzikálnych vzťahov, napríklad tak, ako je popísaný vzťah medzi vyžiarenou energiou a teplotou telesa Planckovým zákonom žiarenia. To je veľmi ťažká úloha, často neriešiteľná, alebo neriešiteľná v krátkom čase. V priemyselnej praxi nám často stačí jednoduchší popis pomocou náhradného matematického modelu, El. S = -14, 59 + 0, 1064 l - 0, 0002 l 2 + 10 -7 l 3 ktorý platí iba v obmedzenom intervale hodnôt vstupov x 1, x 2, . . . , xm a nie je odvodený z fyzikálnych zákonov. Na obrázku vpravo je vzorec (El), ktorý je vyjadrením Planckovho zákona žiarenia absolútne čierneho telesa. Platí v celom rozsahu vlnových dĺžok a teplôt. Trvalo však niekoľko desaťročí, kým Max Planck po neúspešných pokusoch iných fyzikov tento vzťah sformuloval. V rozsahu viditeľného svetla (350 až 750 nm) a pre teplotu 6500 K žiarenie absolútne čierneho telesa dosť dobre popisuje aj polynóm tretieho stupňa (El. S). Postup pri návrhu experimentu 3

Predpoklady experimentu VSTUPY 1. 2. 3. 4. x 2 Proces xm y 2 VÝSTUPY y 1 x 1 yn Vstupy, ktorých vplyv bude predmetom experimentálneho skúmania nazveme faktory (factors). Faktory môžu byť spojité alebo diskrétne. Faktory sa musia dať nastaviť na požadované hodnoty. Hodnoty výstupu pri nastavených hodnotách faktorov nazveme odozvy (responses). Meranie odoziev sa vykoná pri nastavených hodnotách faktorov, ktorým hovoríme úrovne nastavenia faktorov (factor levels). Na popis závislosti y = f(x 1, x 2, . . . , xm) sa použije na obmedzenom intervale hodnôt faktorov náhradný matematický model Ak má proces viac výstupov, každý z výstupov bude mať samostatný model Príklad: Chceme experimentálne zistiť závislosť vyžiarenej energie od vlnovej dĺžky a od teploty telesa. Budeme merať pri teplotách 1000 K a 1500 K a pri vlnových dĺžkach 400, 500 a 600 nm. Hovoríme, že experiment má dva faktory TEPLOTA a VLNOVÁ DĹŽKA. Faktor TEPLOTA je na dvoch úrovniach a faktor VLNOVÁ DĹŽKA ja na troch úrovniach. Postup pri návrhu experimentu 4

Postup pri návrhu experimentu 1. 2. 3. 4. 5. Definovať cieľ experimentu. Definovať team pre návrh experimentu. Zhromaždiť informácie o procese a zariadeniach. Vybrať vhodné charakteristiky procesu, ktoré sú relevantné k definovanému cieľu. Urobiť zoznam všetkých (známych) vplyvov, ktoré môžu byť príčinou zmien určených charakteristík procesu alebo ich variability. 6. Určiť, ktoré z identifikovaných vplyvov budú faktormi experimentu, ktoré budú počas experimentu konštantné, a ktoré budú neriadené a teda budú počas experimentu šumom. Definovať úrovne faktorov a nastavenie tých premenných, ktoré boli definované ako konštanty. 7. Na základe cieľa experimentu, vybraných faktorov a výstupných premenných vybrať vhodný plán pre experiment, určiť počet replikácií a znáhodnenie. 8. Preveriť spôsobilosť meracích systémov. 9. Realizovať experiment. Počas realizácie by mal byť proces v stabilnom stave a definované konštanty by mali byť kontrolované. 10. Analyzovať experimentálne dáta. Odhady efektov, testy hypotéz o významnosti modelu a efektov, predikčná schopnosť modelu (R 2 Adj > 0. 8), overenie sily testov. 11. Overiť výsledky. Dôležitou súčasťou návrhu experimentu je preverenie potrebných zdrojov. Musíme si naplánovať čo všetko je k realizácii experimentu potrebné, vrátane času a finančných potrieb. Náklady na experiment by nemali prevyšovať prínos získaný aplikovaním výsledkov experimentu. Postup pri návrhu experimentu 5

Ciele experimentu Pri experimentovaní nemusí byť vždy našim cieľom nájdenie matematického modelu, ktorý popisuje vzťahy medzi vstupmi a výstupmi. Aj keď sú analytické metódy založené na existencii takéhoto modelu, náš primárny cieľ môže byť napríklad vybrať z veľkého množstva faktorov tie najvýznamnejšie. Podľa cieľa experimentu a charakteru riešeného problému môžeme experimenty rozdeliť do niekoľkých kategórií. • Porovnávacie experimenty (comparative) Pri viacfaktorových experimentoch porovnávame faktory z hľadiska ich vplyvu na výstup. Zaujíma nás, ktoré zo vstupov procesu najviac ovplyvňujú výstup, a teda ktorým venovať najväčšiu pozornosť. • Screening (preosievanie) Pri procesoch s veľkým množstvom vstupov sa snažíme vybrať z nich iba tie podstatné, aby sme znížili počet faktorov pre následný dôslednejší experiment. • Model Primárnym záujmom je nájsť matematický model vzťahov medzi vstupmi a výstupom. • Experimenty pre zmesi (mixture design) Špeciálnym typom experimentov sú experimenty týkajúce sa podielu zložiek v zmesiach. Pretože súčet podielov všetkých zložiek je 1 (alebo 100%), vyžaduje sa osobitný prístup k návrhu experimentu. • Iné ciele • Hľadanie optimálneho nastavenia faktorov Pre hľadanie optimálneho nastavenia faktorov používame metódu odozvovej plochy (response surface method). Výsledkom metódy môže byť hľadané optimum alebo smer, ktorým sa máme uberať v následných experimentoch, aby sme optimum našli. Postup pri návrhu experimentu 6

Výber vstupných a výstupných charakteristík Výstupné charakteristiky musia byť relevantné k definovanému cieľu experimentu, to znamená tie, ktoré sú predmetom riešenia ale aj tie, ktoré by mohli byť nepriaznivo ovplyvnené. Zvolené výstupné premenné by nemali byť podľa možnosti kombináciou viacerých charakteristík procesu. Prednosť dávame spojitým charakteristikám alebo sa snažíme nahradiť charakteristiky typu „vlastnosti“ spojitými charakteristikami. Ak to nie je možné, použijeme aj nespojitú charakteristiku (typu dobrý / zlý). Štatistická analýza je možná, aj keď je výstupom nespojitá premenná. Ako faktory experimentu volíme tie vstupné charakteristiky procesu, u ktorých očakávame vplyv na výstupné charakteristiky a ktoré sú nastaviteľné. Toto nemusí byť vždy na začiatku experimentu jasné a je potrebné realizovať screeningový experiment za účelom výberu faktorov. Je účelné zahrnúť do experimentu čo najviac faktorov, ale táto požiadavka zvyšuje zložitosť experimentu a náklady na experiment, ba dokonca ohrozuje realizovateľnosť experimentu. Teda počet faktorov by mal byť rozumným kompromisom. Prednosť dávame spojitým faktorom alebo sa snažíme nahradiť faktory typu „vlastnosti“ spojitými faktormi. Ak to nie je možné, použijeme aj nespojitý faktor (typu dobrý / zlý). Štatistická analýza je možná, aj keď je použitý nespojitý faktor. Postup pri návrhu experimentu 7

Nastavenie spojitých faktorov Hodnoty, na ktoré sú nastavené faktory pri meraní odoziev počas experimentu, nazývame úrovne (levels) nastavenia faktorov. Ak nastavujeme faktor na dvoch úrovniach, vyššiu úroveň označujeme „+“ a nižšiu úroveň „–“. Ak nastavujeme faktor na troch úrovniach najvyššiu úroveň označujeme „+“, najnižšiu úroveň „–“ a strednú úroveň „ 0“. Pre strednú úroveň platí: stredná úroveň = najvyššia úroveň + najnižšia úroveň 2 Faktory môžu byť nastavované aj na viacerých úrovniach, napríklad pri plánoch CCD. Výpočet úrovní a príslušné označenie bude uvedené pri plánoch CCD. Úrovne nastavenia faktorov musia zodpovedať podmienkam procesu, ktorý je predmetom experimentu. Úrovne musia byť praktické, teda z oblasti kde proces prakticky prebieha alebo môže prebiehať. Úrovne nastavenia faktorov musia byť možné, teda nesmú byť z oblasti, kde by mohlo dochádzať k poškodeniu zariadenia alebo materiálu, alebo kde by proces vôbec nefungoval. Pri voľbe úrovní musíme byť odvážni, ale nie hazardéri (Be bold, but not foolish – literatúra. 1). Úrovne zvolené v zbytočne širokom intervale môžu spôsobiť, že faktor bude vyzerať ako významný aj keď nie je. Naopak príliš úzky interval môže spôsobiť, že faktor je zdanlivo nevýznamný aj keď má v procese významný vplyv. Pre úrovne nastavenia faktorov neexistuje žiaden „vzorec“. Pri ich určení pomôže znalosť procesov a zariadení, prevádzkové skúsenosti alebo výsledky predchádzajúcich experimentov. Postup pri návrhu experimentu 8

Kódovanie úrovní spojitých faktorov °F 33, 8°F 30, 2°F 50 Na obrázku je teplomer, ktorý má dve stupnice. Jednu v stupňoch Celsia a druhú v stupňoch Fahrenheita. Predstavme si, že máme experiment s faktorom TEPLOTA s úrovňami 30, 2°F a 33, 8°F. Tie isté úrovne môžeme používať aj v Celsiovej stupnici, kde budú mať hodnoty -1°C a +1°C. Je isté, že z hľadiska výpočtu sú hodnoty -1 a +1 oveľa príjemnejšie ako hodnoty 30, 2 a 33, 8. °C 10 32 0 14 -10 +1°C Ak tento postup zovšeobecníme, pre ľubovoľné hodnoty veličín, môžeme vytvoriť také stupnice, kde budú mať úrovne nastavenia faktorov práve hodnoty -1 a +1 alebo 0, ak používame tri úrovne faktorov. Tomuto postupu hovoríme kódovanie úrovní. Účelom kódovania nie je len zjednodušenie výpočtov (čo je pri použití počítačov bezpredmetné), ale umožňuje vytvárať tzv. ortogonálne plány experimentov, ktoré sú potrebné pri štatistickej analýze experimentov. -1°C Ak potrebujeme vypočítať iné kódované hodnoty ako úrovne faktorov L– a L+, použijeme vzorec: x – nekódovaná hodnota x. C – kódovaná hodnota Pre dekódovanie použijeme vzorec: Postup pri návrhu experimentu 9

Model pre spojité faktory Ako model budeme používať polynóm 2. stupňa s interakciami. Vzhľadom k tomu, že v experimente musíme počítať aj s experimentálnou chybou, je polynóm doplnený členom, ktorý predstavuje náhodnú premennú s normálnym rozdelením so strednou hodnotou 0 a so smerodajnou odchýlkou se. V mnohých prípadoch bude stačiť lineárny model Člen b 0 v modeli sa nazýva priesečník alebo konštanta (intercept). Člen e je chyba (error). Ostatné členy modelu sa nazývajú efekty faktorov (effects). Efekty, ktoré reprezentujú iba vplyv samotného faktora nezávisle na ostatných faktoroch, sa nazývajú hlavné efekty (main effects). Efekty, v ktorých vystupuje viac faktorov (vo forme súčinu) sa nazývajú interakcie (interactions). Interakcie môžu byť dvojfaktorové (2 -factor interaction), trojfaktorové (3 factor interaction) a podobne. Pretože v modeli je člen e, ktorým je náhodná premenná so strednou hodnotou 0 a so smerodajnou odchýlkou se, bude model dobre popisovať taký proces, kde výstup y má pri každom nastavení faktorov normálne rozdelenie so smerodajnou odchýlkou se, ktorá je nezávislá od nastavenia faktorov. Tomuto predpokladu hovoríme, že rozptyl premennej y je homogénny. Model sa často zjednodušuje. Ako sme už spomenuli, niekedy stačí lineárny model, inokedy len model s hlavnými efektmi. Interakcie v modeli môžu byť veľmi zložité, v praxi však často vystačíme s dvojfaktorovými alebo trojfaktorovými interakciami. Postup pri návrhu experimentu 10

Množstvo dát Ak predpokladáme iba lineárny vplyv faktora, bude v modeli zastúpený iba lineárnym členom a príslušnými interakciami. Pre meranie odoziev musí byť faktor nastavený minimálne na dvoch úrovniach (lineárna funkcia je definovaná dvomi bodmi). Ak predpokladáme nelineárny vplyv faktora, bude v modeli zastúpený lineárnym členom, kvadratickým členom a príslušnými interakciami. Nelinearity by sa mohli popisovať aj vyššími ako kvadratickými členmi, ale v praxi sa používajú len výnimočne. Pre meranie odoziev musí byť faktor nastavený minimálne na troch úrovniach (kvadratická funkcia je definovaná tromi bodmi). Ak bude mať experiment p faktorov na dvoch úrovniach a q faktorov na troch úrovniach, počet členov v úplnom modeli bude: Pre odhad koeficientov b v tomto modeli je potrebných najmenej k nezávislých, vhodne zostavených kombinácií faktorov a príslušných odoziev. Pre odhad smerodajnej odchýlky se sú potrebné najmenej dve merania odozvy pri tom istom nastavení faktorov. Predpis, ktorý definuje nastavenia faktorov tak, aby sa dali odhadnúť koeficienty plán experimentu (plan). Postup pri návrhu experimentu b v modeli sa nazýva 11

Dvojúrovňový úplný faktorový plán experimentu – n V tabuľkách sú úplné faktorové plány na dvoch úrovniach faktorov. Postup zostavenia plánov je zrejmý z tabuliek. Dôležité je všimnúť si, že m + 1 faktorový plán dostaneme z m faktorového jeho zdvojením a pridaním stĺpca pre ďalší faktor, ako je vyznačené v tabuľke vpravo. Úplný model pre dva faktory na dvoch úrovniach má 4 členy ak neuvažujeme chybu. Na nájdenie štyroch koeficientov b v modeli potrebujeme zostaviť sústavu štyroch lineárne nezávislých lineárnych rovníc. Nastavenia faktorov v týchto rovniciach tvoria plán experimentu. Sú použité kódované úrovne faktorov a hodnoty tvoriace plán sú vyznačené hrubým písmom. y(1) = b 0 + b 1(– 1) + b 2(– 1) + b 12(– 1) Test x 1 x 2 x 3 y(2) = b 0 + b 1(– 1) + b 2(+1) + b 12(– 1)(+1) 1 y(3) = b 0 + b 1(+1) + b 2(– 1) + b 12(+1)(– 1) 2 + y(4) = b 0 + b 1(+1) + b 2(+1) + b 12(+1) 3 + Test x 1 x 2 4 + + 5 + 1 6 + + 2 + 7 + + 3 + 8 + + + 4 + + Ak je k členov v úplnom lineárnom modeli, úplný faktorový plán má k riadkov. Ak je súčasťou modelu aj chyba, na riešenie treba použiť metódu najmenších štvorcov. Postup pri návrhu experimentu Test x 1 x 2 x 3 x 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 + + + + + + + + 12

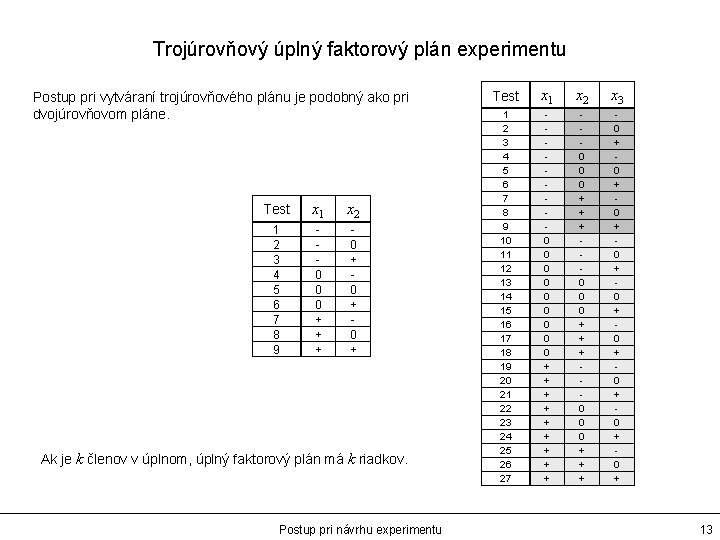
Trojúrovňový úplný faktorový plán experimentu Postup pri vytváraní trojúrovňového plánu je podobný ako pri dvojúrovňovom pláne. Test x 1 x 2 1 2 3 4 5 6 7 8 9 0 0 0 + + + 0 + 0 + Ak je k členov v úplnom, úplný faktorový plán má k riadkov. Postup pri návrhu experimentu Test x 1 x 2 x 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 0 0 0 0 0 + + + + + 0 0 0 + + + 0 + 0 + 0 + 13

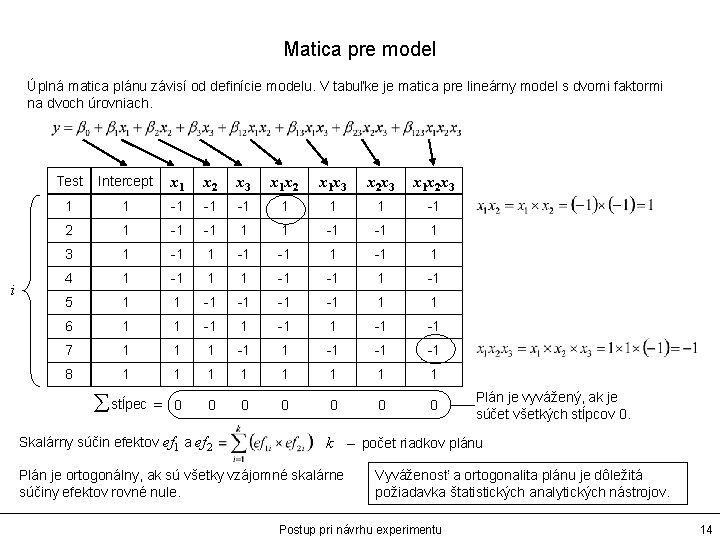
Matica pre model Úplná matica plánu závisí od definície modelu. V tabuľke je matica pre lineárny model s dvomi faktormi na dvoch úrovniach. i Test Intercept x 1 x 2 x 3 x 1 x 2 x 1 x 3 x 2 x 3 x 1 x 2 x 3 1 1 -1 -1 -1 2 1 -1 -1 1 3 1 -1 -1 1 4 1 -1 1 1 -1 -1 5 1 1 -1 -1 1 1 6 1 1 -1 -1 7 1 1 1 -1 -1 -1 8 1 1 1 1 åstĺpec = 0 0 0 0 Skalárny súčin efektov ef 1 a ef 2 Plán je vyvážený, ak je súčet všetkých stĺpcov 0. k – počet riadkov plánu Plán je ortogonálny, ak sú všetky vzájomné skalárne súčiny efektov rovné nule. Vyváženosť a ortogonalita plánu je dôležitá požiadavka štatistických analytických nástrojov. Postup pri návrhu experimentu 14

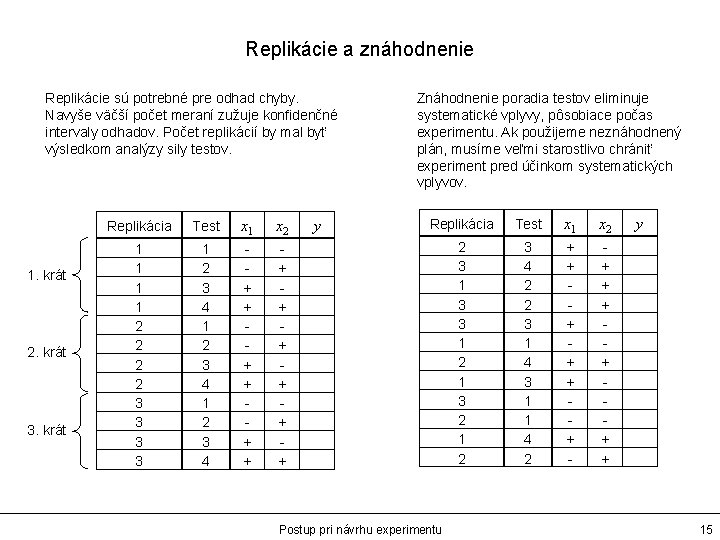
Replikácie a znáhodnenie Replikácie sú potrebné pre odhad chyby. Navyše väčší počet meraní zužuje konfidenčné intervaly odhadov. Počet replikácií by mal byť výsledkom analýzy sily testov. 1. krát 2. krát 3. krát Replikácia Test x 1 x 2 1 1 2 2 3 3 1 2 3 4 + + + y Znáhodnenie poradia testov eliminuje systematické vplyvy, pôsobiace počas experimentu. Ak použijeme neznáhodnený plán, musíme veľmi starostlivo chrániť experiment pred účinkom systematických vplyvov. Replikácia Test x 1 x 2 2 3 1 3 3 1 2 1 3 2 1 2 3 4 2 2 3 1 4 3 1 1 4 2 + + + - + + + Postup pri návrhu experimentu y 15

Počet replikácií Pre naše účely budeme označovať každú realizáciu základného plánu ako jednu replikáciu. Teda prvé meranie plánu ako prvú replikáciu atď. (V niektorých literatúrach sa prvá realizácia základného plánu neoznačuje ako replikácia, resp. ako replikácia 0. ) Za replikáciu sa považuje znovu realizácia plánu alebo jednotlivého testu len v prípade, že boli znovu nastavené hodnoty faktorov po realizácii iných testoch. V prípade, že ide len o opakované merania pri tom istom nastavení, výsledky sa nepovažujú za výsledky získané z replikácií ale len výsledky z opakovaných meraní. Počet replikácií (v horšom prípade opakovaných meraní) by mal byť najmenej 2. Inak nie je možné odhadnúť experimentálnu chybu. S väčším počtom replikácií rastie dôveryhodnosť odhadov. Správne by mal byť počet replikácií určený na základe analýzy sily testu a veľkosti vzorky ako bolo uvedené v kapitole o testoch štatistických hypotéz. Ak nerealizujeme replikácie, ale iba opakované merania, zistená experimentálna chyba môže byť zdanlivo menšia ako v skutočnosti. Postup pri návrhu experimentu 16

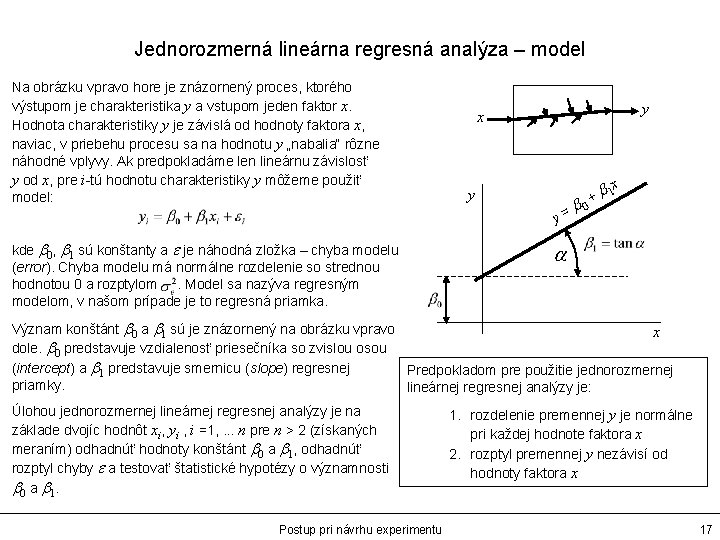
Jednorozmerná lineárna regresná analýza – model Na obrázku vpravo hore je znázornený proces, ktorého výstupom je charakteristika y a vstupom jeden faktor x. Hodnota charakteristiky y je závislá od hodnoty faktora x, naviac, v priebehu procesu sa na hodnotu y „nabalia“ rôzne náhodné vplyvy. Ak predpokladáme len lineárnu závislosť y od x, pre i-tú hodnotu charakteristiky y môžeme použiť model: y x x y y= kde b 0, b 1 sú konštanty a e je náhodná zložka – chyba modelu (error). Chyba modelu má normálne rozdelenie so strednou hodnotou 0 a rozptylom. Model sa nazýva regresným modelom, v našom prípade je to regresná priamka. b 0 + b 1 a Význam konštánt b 0 a b 1 sú je znázornený na obrázku vpravo x dole. b 0 predstavuje vzdialenosť priesečníka so zvislou osou (intercept) a b 1 predstavuje smernicu (slope) regresnej Predpokladom pre použitie jednorozmernej priamky. lineárnej regresnej analýzy je: Úlohou jednorozmernej lineárnej regresnej analýzy je na základe dvojíc hodnôt xi, yi , i =1, . . . n pre n > 2 (získaných meraním) odhadnúť hodnoty konštánt b 0 a b 1, odhadnúť rozptyl chyby e a testovať štatistické hypotézy o významnosti b 0 a b 1. Postup pri návrhu experimentu 1. rozdelenie premennej y je normálne pri každej hodnote faktora x 2. rozptyl premennej y nezávisí od hodnoty faktora x 17

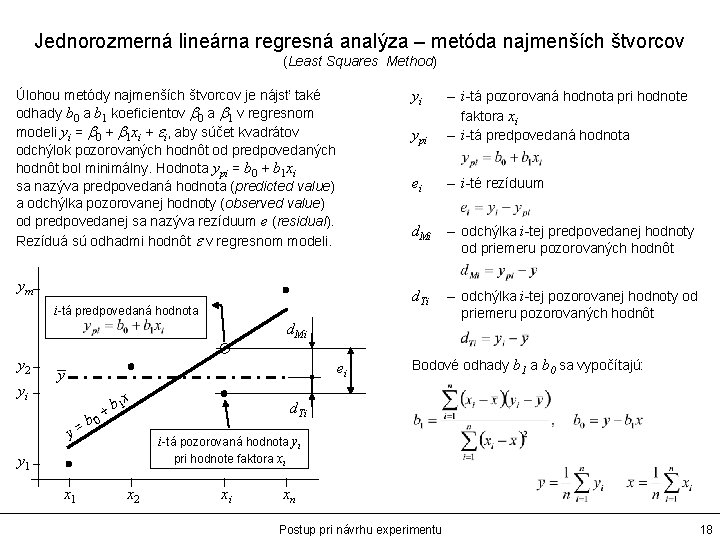
Jednorozmerná lineárna regresná analýza – metóda najmenších štvorcov (Least Squares Method) Úlohou metódy najmenších štvorcov je nájsť také odhady b 0 a b 1 koeficientov b 0 a b 1 v regresnom modeli yi = b 0 + b 1 xi + ei, aby súčet kvadrátov odchýlok pozorovaných hodnôt od predpovedaných hodnôt bol minimálny. Hodnota ypi = b 0 + b 1 xi sa nazýva predpovedaná hodnota (predicted value) a odchýlka pozorovanej hodnoty (observed value) od predpovedanej sa nazýva rezíduum e (residual). Rezíduá sú odhadmi hodnôt e v regresnom modeli. yi ypi – i-tá pozorovaná hodnota pri hodnote faktora xi – i-tá predpovedaná hodnota ei – i-té rezíduum d. Mi – odchýlka i-tej predpovedanej hodnoty od priemeru pozorovaných hodnôt ym d. Ti i-tá predpovedaná hodnota d. Mi y 2 yi ei y y 0 =b x 1 b + Bodové odhady b 1 a b 0 sa vypočítajú: d. Ti i-tá pozorovaná hodnota yi pri hodnote faktora xi y 1 x 1 – odchýlka i-tej pozorovanej hodnoty od priemeru pozorovaných hodnôt x 2 xi xn Postup pri návrhu experimentu 18

Jednorozmerná lineárna regresná analýza – ANOVA analyzuje zložky rozptylu výstupnej premennej y. Časť rozptylu, ktorá sa dá prisúdiť vplyvu faktora x sa nazýva vysvetlený rozptyl (explained variance) a zvyšný, nevysvetlený rozptyl, je reziduálny rozptyl (residual variance). V prípade, že faktor x nemá vplyv na výstupnú premennú y, MSM a MSe z tabuľky ANOVA sú nezávislými odhadmi rozptylu náhodných vplyvov, ktoré spôsobujú rozptýlenosť hodnôt yi. F-testom sa testuje hypotéza: Model Rezíduá Total df SS MS F p-hodnota 1 SSM MSM / MSe n-2 SSe MSe p-hodnota sa vypočíta rovnako n-1 SST MST ako pri jednofaktorovej metóde ANOVA Ak je H 0 zamietnutá, znamená to, že MSM je väčší ako by mohol byť iba z dôvodu náhodných vplyvov a že je dôsledkom vplyvu faktora x. Ak je regresný model potom vplyv faktora x znamená nenulovú hodnotu koeficientu b 1 a testovaná hypotéza sa dá upraviť nasledovne: Zamietnutie H 0 znamená zamietnutie. Potom hovoríme, že model je štatisticky významný. MSe je odhadom rozptylu chyby modelu e. SSe – súčet štvorcov odchýlok rezíduí SSM SST (residual, error sum of squares) – súčet štvorcov odchýlok pre model (model sum of squares) – celkový súčet štvorcov odchýlok (total sum of squares) Postup pri návrhu experimentu 19

Jednorozmerná lineárna regresná analýza – odhady b 0 a b 1 sú bodovými odhadmi koeficientov b 0 a b 1 regresného modelu. Konfidenčné intervaly pre úroveň spoľahlivosti 1 – a sú definované: znamená 1 – a/2 kvantil Studentovho rozdelenia (t-rozdelenie) pre n – 2 stupňov voľnosti. Postup pri návrhu experimentu 20

Jednorozmerná lineárna regresná analýza – t-test pre b 1 t-test pre b 0 Okrem F-testu v ANOVA môžeme použiť na test štatistickej významnosti koeficientu b 1 aj t-test. Testová štatistika je Podobne môžeme použiť t-test aj na testovanie štatistickej významnosti koeficientu b 0. Testová štatistika je Testujeme hypotézu: Ft – distribučná funkcia t-rozdelenia Postup pri návrhu experimentu 21

Jednorozmerná lineárna regresná analýza – koeficient determinácie V prípade, že model dokonale popisuje pozorované hodnoty, odhadom celkového rozptylu výstupnej premennej y, je výberový rozptyl predpovedaných hodnôt yp 1, . . . , ypn : Pomer modelom vysvetleného súčtu štvorcov SSM a celkového súčtu štvorcov SST je mierou zhody pozorovaných hodnôt s modelom, nazýva sa koeficient determinácie (coefficient of determination) a označuje sa R 2. V iných prípadoch je odhadom celkového rozptylu výberový rozptyl pozorovaných hodnôt y 1, . . . , yn : V prípade, že model dokonale popisuje pozorované hodnoty, reziduálny rozptyl je 0 a platí pre i = 1. . . n. Potom . Ak model nepopisuje pozorované hodnoty dokonale, je zväčšený o reziduálny rozptyl a. Výraz sa dá upraviť: Koeficient determinácie nadobúda hodnoty: Dokonalý model vysvetľuje celý celkový rozptyl. V tomto prípade je R 2 = 1. Za dobrý sa považuje taký model, pre ktorý je R 2 0, 8. Postup pri návrhu experimentu 22

Jednorozmerná lineárna regresná analýza – predikcia Na základe odhadu regresného modelu môžeme predpovedať hodnoty výstupnej premennej y pre dané hodnoty faktora x. Tomuto predpovedaniu, presnejšie odhadom týchto predpovedí hovoríme predikcia (prediction). Bodovým odhadom predpovede y. A pre hodnotu faktora x. A je : Konfidenčný interval pre strednú hodnotu m. A s úrovňou spoľahlivosti 1 – a je (používa sa aj termín – konfidenčný interval pre model): Individuálne hodnoty y. Ai zistené pri nastavení faktora x. A budú s pravdepodobnosťou 1 – a v intervale, ktorý sa nazýva predikčný interval (prediction interval): znamená 1 – a/2 kvantil Studentovho rozdelenia (t-rozdelenie) pre n – 2 stupňov voľnosti. Postup pri návrhu experimentu 23

Jednorozmerná lineárna regresná analýza – závislosť šírky konfidenčného a predikčného intervalu od n Preskúmajme vzorec pre konfidenčný interval pre model. V zátvorke pod odmocninou sú dva zlomky: 1/n a člen, ktorý má v menovateli súčet štvorcov odchýlok faktora x. Obidva menovatele sa budú s rastúcim n zväčšovať, teda zlomky sa budú zmenšovať a konfidenčný interval sa bude zužovať. Vzorec predikčný interval pre individuálne hodnoty obsahuje v zátvorke pod odmocninou ešte jeden konštantný člen 1. Pre malé n sa síce bude hodnota v zátvorke zmenšovať, ale pre väčšie n už budú hodnoty zlomkov oveľa menšie ako jedna a hodnota zátvorky bude daná len konštantou 1. Šírka predikčného intervalu teda len veľmi málo závisí od n, a je daná hlavne hodnotou MSe. Pre väčšie n je prakticky konštantná. Konfidenčný interval pre model môžeme zužovať použitím väčšieho počtu hodnôt. Šírka predikčného intervalu pre individuálne hodnoty prakticky závisí len od reziduálneho rozptylu MSe. Postup pri návrhu experimentu 24

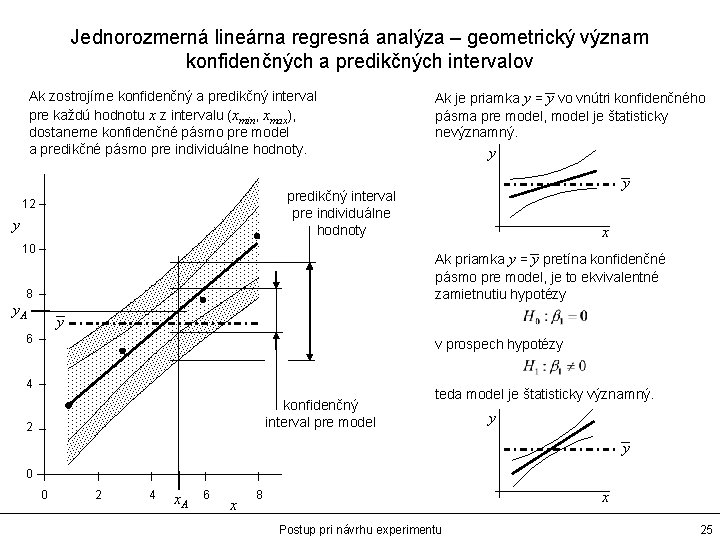
Jednorozmerná lineárna regresná analýza – geometrický význam konfidenčných a predikčných intervalov Ak zostrojíme konfidenčný a predikčný interval pre každú hodnotu x z intervalu (xmin, xmax), dostaneme konfidenčné pásmo pre model a predikčné pásmo pre individuálne hodnoty. Ak je priamka y = y vo vnútri konfidenčného pásma pre model, model je štatisticky nevýznamný. y y predikčný interval pre individuálne hodnoty 12 y 10 x Ak priamka y = y pretína konfidenčné pásmo pre model, je to ekvivalentné zamietnutiu hypotézy 8 y. A y 6 v prospech hypotézy 4 konfidenčný interval pre model 2 teda model je štatisticky významný. y y 0 0 2 4 x. A 6 x x 8 Postup pri návrhu experimentu 25

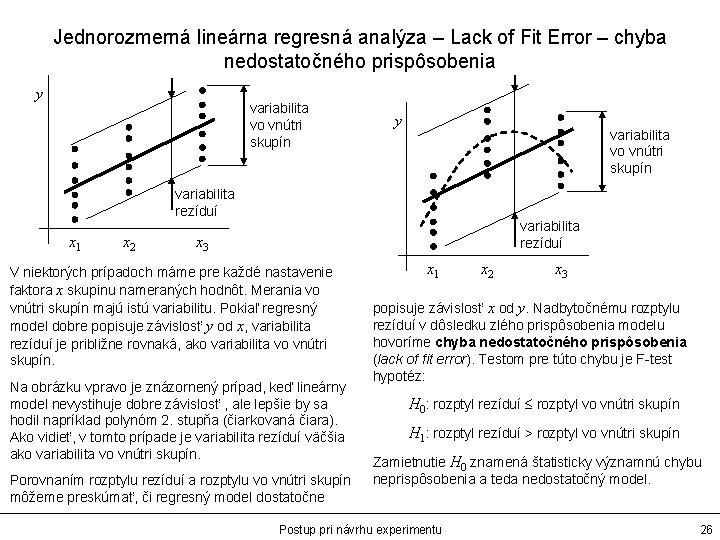
Jednorozmerná lineárna regresná analýza – Lack of Fit Error – chyba nedostatočného prispôsobenia y variabilita vo vnútri skupín variabilita rezíduí x 1 x 2 variabilita rezíduí x 3 V niektorých prípadoch máme pre každé nastavenie faktora x skupinu nameraných hodnôt. Merania vo vnútri skupín majú istú variabilitu. Pokiaľ regresný model dobre popisuje závislosť y od x, variabilita rezíduí je približne rovnaká, ako variabilita vo vnútri skupín. Na obrázku vpravo je znázornený prípad, keď lineárny model nevystihuje dobre závislosť , ale lepšie by sa hodil napríklad polynóm 2. stupňa (čiarkovaná čiara). Ako vidieť, v tomto prípade je variabilita rezíduí väčšia ako variabilita vo vnútri skupín. Porovnaním rozptylu rezíduí a rozptylu vo vnútri skupín môžeme preskúmať, či regresný model dostatočne x 1 x 2 x 3 popisuje závislosť x od y. Nadbytočnému rozptylu rezíduí v dôsledku zlého prispôsobenia modelu hovoríme chyba nedostatočného prispôsobenia (lack of fit error). Testom pre túto chybu je F-test hypotéz: H 0: rozptyl rezíduí rozptyl vo vnútri skupín H 1: rozptyl rezíduí > rozptyl vo vnútri skupín Zamietnutie H 0 znamená štatisticky významnú chybu neprispôsobenia a teda nedostatočný model. Postup pri návrhu experimentu 26

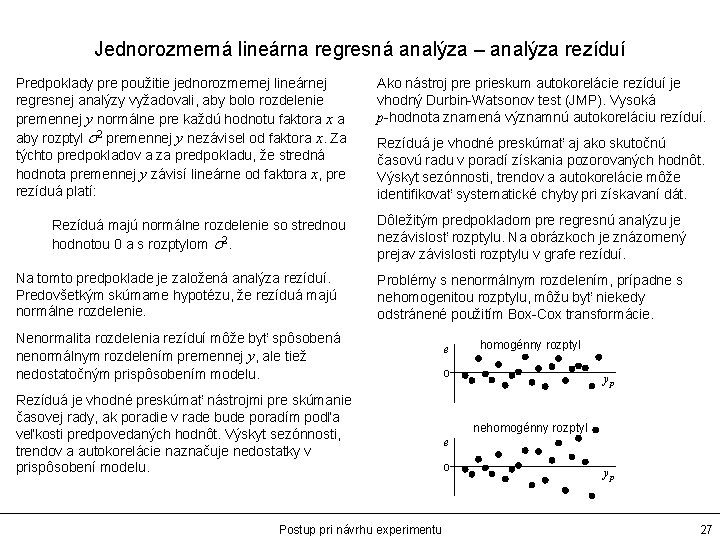
Jednorozmerná lineárna regresná analýza – analýza rezíduí Predpoklady pre použitie jednorozmernej lineárnej regresnej analýzy vyžadovali, aby bolo rozdelenie premennej y normálne pre každú hodnotu faktora x a aby rozptyl s 2 premennej y nezávisel od faktora x. Za týchto predpokladov a za predpokladu, že stredná hodnota premennej y závisí lineárne od faktora x, pre rezíduá platí: Rezíduá majú normálne rozdelenie so strednou hodnotou 0 a s rozptylom s 2. Na tomto predpoklade je založená analýza rezíduí. Predovšetkým skúmame hypotézu, že rezíduá majú normálne rozdelenie. Ako nástroj pre prieskum autokorelácie rezíduí je vhodný Durbin-Watsonov test (JMP). Vysoká p-hodnota znamená významnú autokoreláciu rezíduí. Rezíduá je vhodné preskúmať aj ako skutočnú časovú radu v poradí získania pozorovaných hodnôt. Výskyt sezónnosti, trendov a autokorelácie môže identifikovať systematické chyby pri získavaní dát. Dôležitým predpokladom pre regresnú analýzu je nezávislosť rozptylu. Na obrázkoch je znázornený prejav závislosti rozptylu v grafe rezíduí. Problémy s nenormálnym rozdelením, prípadne s nehomogenitou rozptylu, môžu byť niekedy odstránené použitím Box-Cox transformácie. Nenormalita rozdelenia rezíduí môže byť spôsobená nenormálnym rozdelením premennej y, ale tiež nedostatočným prispôsobením modelu. Rezíduá je vhodné preskúmať nástrojmi pre skúmanie časovej rady, ak poradie v rade bude poradím podľa veľkosti predpovedaných hodnôt. Výskyt sezónnosti, trendov a autokorelácie naznačuje nedostatky v prispôsobení modelu. Postup pri návrhu experimentu e homogénny rozptyl 0 yp nehomogénny rozptyl e 0 yp 27

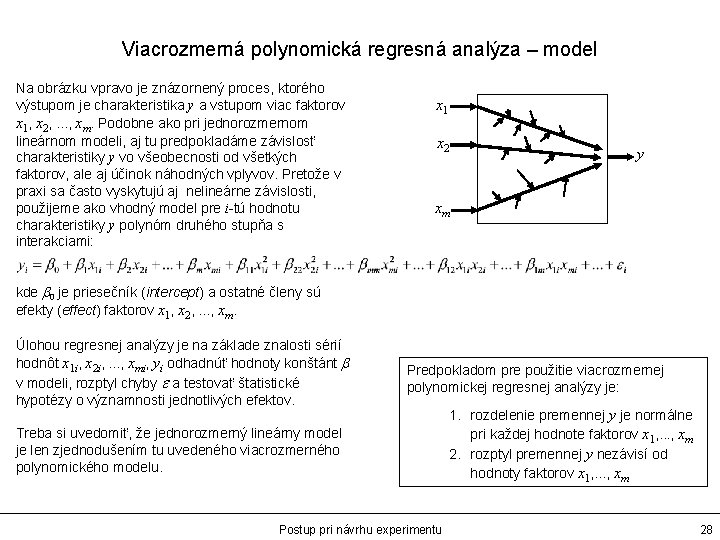
Viacrozmerná polynomická regresná analýza – model Na obrázku vpravo je znázornený proces, ktorého výstupom je charakteristika y a vstupom viac faktorov x 1, x 2, . . . , xm. Podobne ako pri jednorozmernom lineárnom modeli, aj tu predpokladáme závislosť charakteristiky y vo všeobecnosti od všetkých faktorov, ale aj účinok náhodných vplyvov. Pretože v praxi sa často vyskytujú aj nelineárne závislosti, použijeme ako vhodný model pre i-tú hodnotu charakteristiky y polynóm druhého stupňa s interakciami: x 1 x 2 y xm kde b 0 je priesečník (intercept) a ostatné členy sú efekty (effect) faktorov x 1, x 2, . . . , xm. Úlohou regresnej analýzy je na základe znalosti sérií hodnôt x 1 i, x 2 i, . . . , xmi, yi odhadnúť hodnoty konštánt b v modeli, rozptyl chyby e a testovať štatistické hypotézy o významnosti jednotlivých efektov. Predpokladom pre použitie viacrozmernej polynomickej regresnej analýzy je: Treba si uvedomiť, že jednorozmerný lineárny model je len zjednodušením tu uvedeného viacrozmerného polynomického modelu. Postup pri návrhu experimentu 1. rozdelenie premennej y je normálne pri každej hodnote faktorov x 1, . . . , xm 2. rozptyl premennej y nezávisí od hodnoty faktorov x 1, . . . , xm 28

Viacrozmerná polynomická regresná analýza – interakcia Členy z modelu na predchádzajúcej strane, v ktorých sa vyskytuje súčin faktorov, sa nazývajú interakcie. Na tejto strane chceme objasniť význam interakcie v modeli. x 1 y Vpravo je znázornený proces, ktorého vstupom sú dva faktory x 1 a x 2. Ak predpokladáme lineárnu závislosť, môžeme ju popísať modelom: Koeficienty však môžu byť tiež závislé od faktorov, a to tak, že x 1 ovplyvňuje a x 2 ovplyvňuje. Koeficienty už nebudú konštantami a model sa zmení: x 2 Po označení dostaneme konečný tvar modelu: Označme Potom môžeme model upraviť: Vidíme, že k pôvodnému modelu pribudol efekt interakcie, ktorý je dôsledkom vzájomného ovplyvňovania pôsobenia faktorov. Postup pri návrhu experimentu 29

Viacrozmerná polynomická regresná analýza – metóda najmenších štvorcov, množstvo dát Metóda najmenších štvorcov vo viacrozmernej polynomickej regresnej analýze, tak ako v jednorozmernej regresnej analýze, minimalizuje súčet štvorcov odchýlok pozorovaných hodnôt od predpovedaných. Vzhľadom k tomu, že model je viacrozmerný, a že sa v ňom nachádzajú nelineárne členy a interakcie, sú isté požiadavky na hodnoty nastavení faktorov tak, aby bola úloha minimalizácie súčtu štvorcov riešiteľná. Konštrukcia plánov, ktoré definujú nastavenia faktorov x 1, x 2, . . . , xm, je predmetom metodiky návrhu experimentov (DOE, design of experiment). Vo všeobecnosti platí, že ak je v modeli k členov, vrátane interceptu, potrebujeme k vyriešeniu minimalizácie súčtu štvorcov najmenej k nezávislých vhodne zostavených kombinácií nastavení faktorov a pri týchto nastaveniach získaných hodnôt y. Ak chceme odhadnúť aj rozptyl chyby e, potrebujeme viac ako k nezávislých kombinácií nastavení faktorov, alebo opakované merania pri tých istých nastaveniach. Ak plán nastavenia faktorov nezodpovedá modelu, úloha minimalizácie nie je riešiteľná, pretože matica bude mať lineárne závislé riadky – kolineárne (collinearity), a matica bude singulárna (singularity). Napríklad v softvéri JMP je tento fakt oznámený tabuľkou „Singularity Details“, kde sú uvedené efekty v modeli, ktoré sú príčinou neriešiteľnosti. Postup pri návrhu experimentu 30

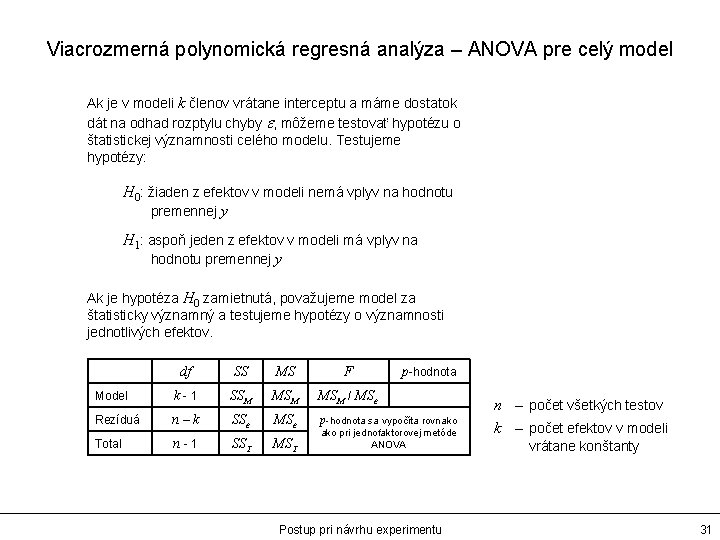
Viacrozmerná polynomická regresná analýza – ANOVA pre celý model Ak je v modeli k členov vrátane interceptu a máme dostatok dát na odhad rozptylu chyby e, môžeme testovať hypotézu o štatistickej významnosti celého modelu. Testujeme hypotézy: H 0: žiaden z efektov v modeli nemá vplyv na hodnotu premennej y H 1: aspoň jeden z efektov v modeli má vplyv na hodnotu premennej y Ak je hypotéza H 0 zamietnutá, považujeme model za štatisticky významný a testujeme hypotézy o významnosti jednotlivých efektov. df SS MS F p-hodnota Model k-1 SSM MSM / MSe Rezíduá n–k SSe MSe p-hodnota sa vypočíta rovnako Total n-1 SST MST ako pri jednofaktorovej metóde ANOVA Postup pri návrhu experimentu n – počet všetkých testov k – počet efektov v modeli vrátane konštanty 31

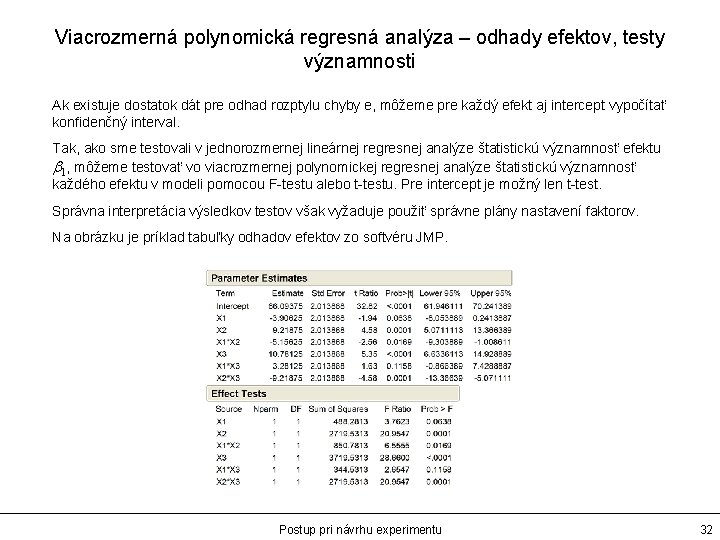
Viacrozmerná polynomická regresná analýza – odhady efektov, testy významnosti Ak existuje dostatok dát pre odhad rozptylu chyby e, môžeme pre každý efekt aj intercept vypočítať konfidenčný interval. Tak, ako sme testovali v jednorozmernej lineárnej regresnej analýze štatistickú významnosť efektu b 1, môžeme testovať vo viacrozmernej polynomickej regresnej analýze štatistickú významnosť každého efektu v modeli pomocou F-testu alebo t-testu. Pre intercept je možný len t-test. Správna interpretácia výsledkov testov však vyžaduje použiť správne plány nastavení faktorov. Na obrázku je príklad tabuľky odhadov efektov zo softvéru JMP. Postup pri návrhu experimentu 32

Viacrozmerná polynomická regresná analýza – upravený koeficient determinácie Hodnota koeficientu determinácie sa môže zvyšovať s rastúcim počtom efektov v modeli, pretože model sa dokáže lepšie „pozatáčať“ pomedzi pozorované hodnoty, aj keď to nezodpovedá skutočnej závislosti. Preto sa na vyjadrenie miery súhlasu modelu s pozorovanými hodnotami používa upravený koeficient determinácie (R square adjusted), definovaný: Ako vidieť zo vzorca, R 2 musí pri väčšom počte stupňov voľnosti modelu df. M dosahovať vyššie hodnoty, aby sa dosiahla dostatočná hodnota. Upravený koeficient determinácie môže v extrémnych prípadoch nadobúdať záporné hodnoty. Vtedy ho treba považovať za nulu. Postup pri návrhu experimentu 33

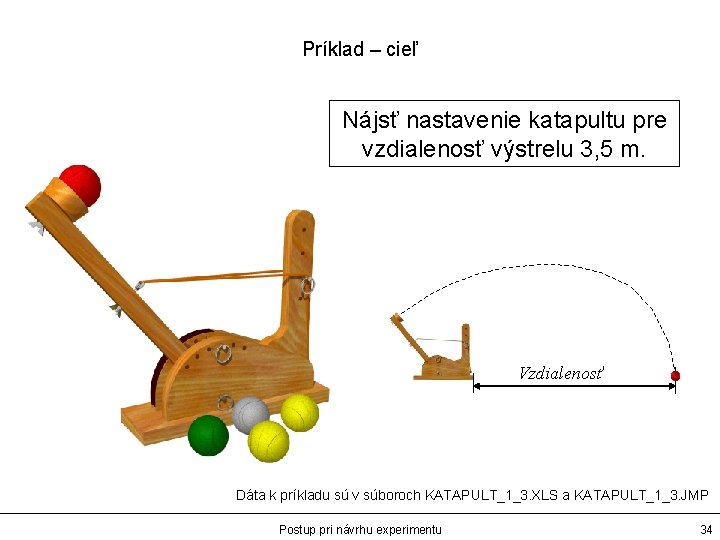
Príklad – cieľ Nájsť nastavenie katapultu pre vzdialenosť výstrelu 3, 5 m. Vzdialenosť Dáta k príkladu sú v súboroch KATAPULT_1_3. XLS a KATAPULT_1_3. JMP Postup pri návrhu experimentu 34

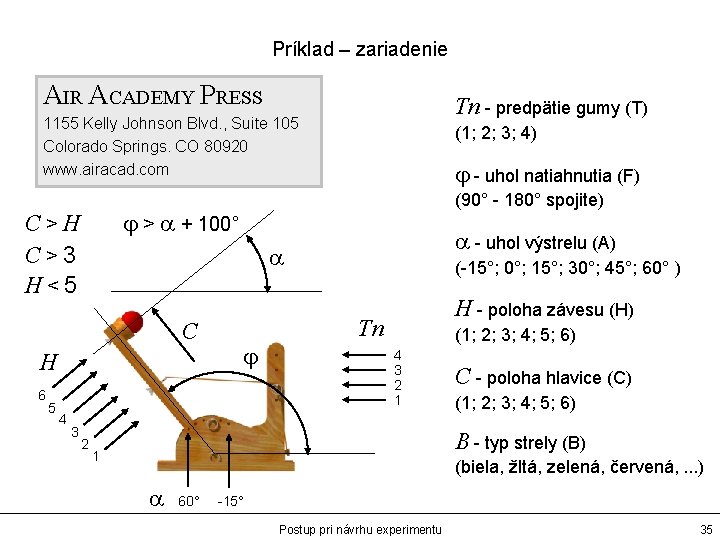
Príklad – zariadenie AIR ACADEMY PRESS Tn - predpätie gumy (T) 1155 Kelly Johnson Blvd. , Suite 105 Colorado Springs. CO 80920 www. airacad. com H 4 3 (90° - 180° spojite) a - uhol výstrelu (A) a C 5 j - uhol natiahnutia (F) j > a + 100° C>H C>3 H<5 6 (1; 2; 3; 4) 2 j (-15°; 0°; 15°; 30°; 45°; 60° ) H - poloha závesu (H) Tn (1; 2; 3; 4; 5; 6) 4 3 2 1 C - poloha hlavice (C) (1; 2; 3; 4; 5; 6) B - typ strely (B) 1 (biela, žltá, zelená, červená, . . . ) a 60° -15° Postup pri návrhu experimentu 35

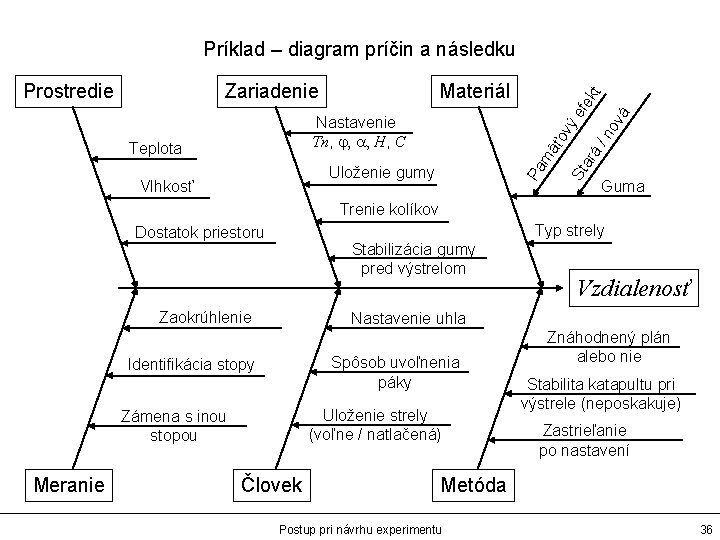
Príklad – diagram príčin a následku Uloženie gumy Vlhkosť /n ov á efe ar á mä Teplota ťo vý Nastavenie Tn, j, a, H, C kt Materiál St Zariadenie Pa Prostredie Guma Trenie kolíkov Typ strely Dostatok priestoru Stabilizácia gumy pred výstrelom Zaokrúhlenie Nastavenie uhla Spôsob uvoľnenia páky Identifikácia stopy Uloženie strely (voľne / natlačená) Zámena s inou stopou Meranie Vzdialenosť Človek Znáhodnený plán alebo nie Stabilita katapultu pri výstrele (neposkakuje) Zastrieľanie po nastavení Metóda Postup pri návrhu experimentu 36

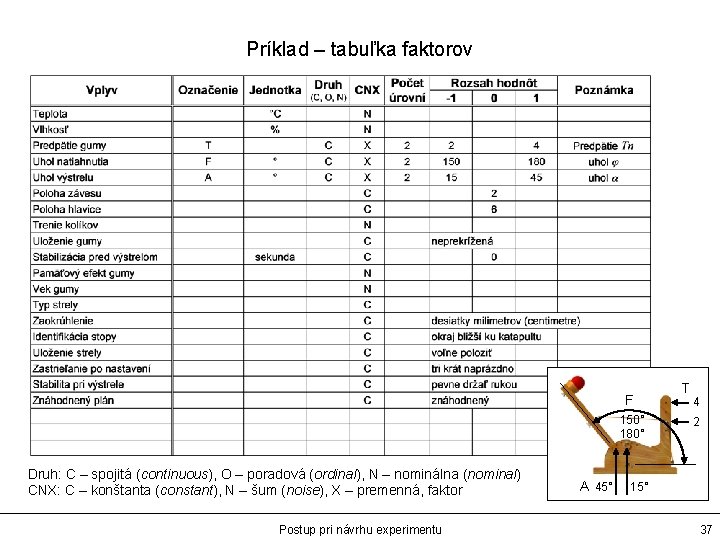
Príklad – tabuľka faktorov F 150° 180° Druh: C – spojitá (continuous), O – poradová (ordinal), N – nominálna (nominal) CNX: C – konštanta (constant), N – šum (noise), X – premenná, faktor Postup pri návrhu experimentu A 45° T 4 2 15° 37

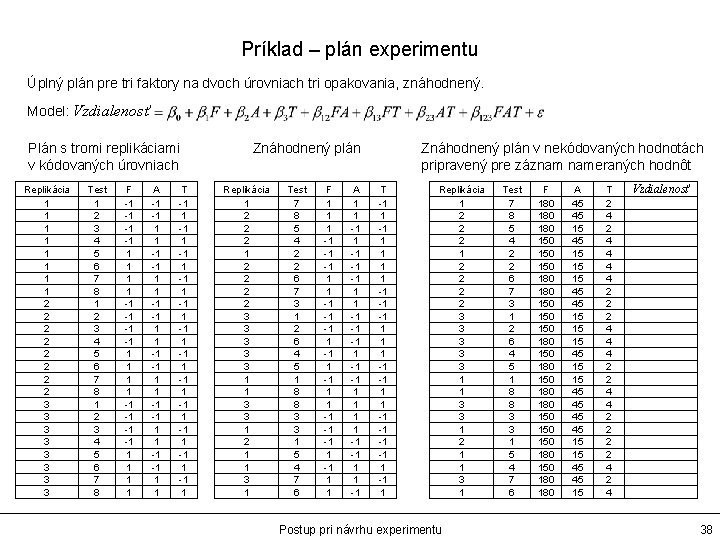
Príklad – plán experimentu Úplný plán pre tri faktory na dvoch úrovniach tri opakovania, znáhodnený. Model: Vzdialenosť Plán s tromi replikáciami v kódovaných úrovniach Replikácia 1 1 1 1 2 2 2 2 3 3 3 3 Test 1 2 3 4 5 6 7 8 F -1 -1 1 1 1 1 -1 -1 1 1 A -1 -1 1 1 -1 -1 1 1 T -1 1 -1 1 -1 1 Znáhodnený plán Replikácia 1 2 2 2 2 3 3 3 1 1 3 3 1 2 1 1 3 1 Test 7 8 5 4 2 2 6 7 3 1 2 6 4 5 1 8 8 3 3 1 5 4 7 6 F 1 1 1 -1 -1 -1 1 1 -1 -1 -1 1 1 A 1 1 -1 -1 -1 1 1 -1 -1 1 1 -1 Znáhodnený plán v nekódovaných hodnotách pripravený pre záznam nameraných hodnôt T -1 1 1 1 1 -1 -1 -1 1 -1 1 Replikácia 1 2 2 2 2 3 3 3 1 1 3 3 1 2 1 1 3 1 Postup pri návrhu experimentu Test 7 8 5 4 2 2 6 7 3 1 2 6 4 5 1 8 8 3 3 1 5 4 7 6 F 180 180 150 150 150 180 180 150 150 180 180 A 45 45 15 15 15 45 45 15 15 45 45 15 T 2 4 4 4 4 2 2 2 2 4 Vzdialenosť 38

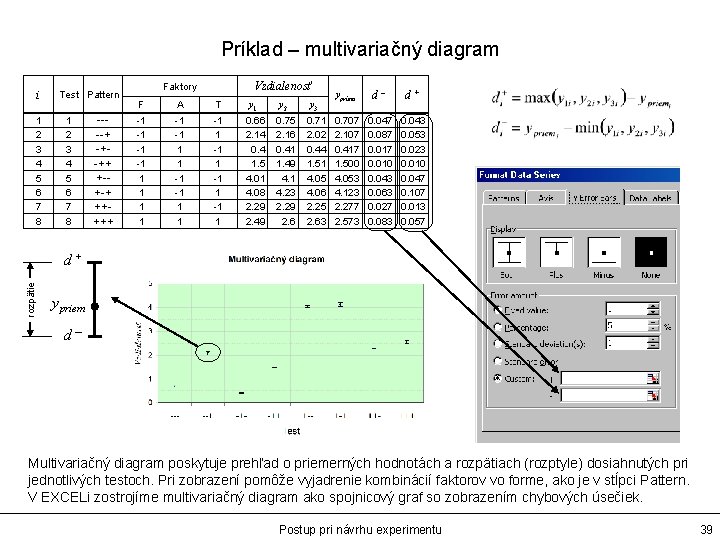
Príklad – multivariačný diagram i 1 2 3 4 5 6 7 8 Test Pattern 1 2 3 4 5 6 7 8 ----+ -+-++ +-+-+ +++++ Vzdialenosť Faktory F A T y 1 y 2 y 3 -1 -1 1 1 -1 1 0. 66 2. 14 0. 4 1. 5 4. 01 4. 08 2. 29 2. 49 0. 75 2. 16 0. 41 1. 49 4. 1 4. 23 2. 29 2. 6 0. 71 2. 02 0. 44 1. 51 4. 05 4. 06 2. 25 2. 63 ypriem d– d+ 0. 707 2. 107 0. 417 1. 500 4. 053 4. 123 2. 277 2. 573 0. 047 0. 087 0. 010 0. 043 0. 063 0. 027 0. 083 0. 043 0. 053 0. 023 0. 010 0. 047 0. 107 0. 013 0. 057 rozpätie d+ ypriem d– Multivariačný diagram poskytuje prehľad o priemerných hodnotách a rozpätiach (rozptyle) dosiahnutých pri jednotlivých testoch. Pri zobrazení pomôže vyjadrenie kombinácií faktorov vo forme, ako je v stĺpci Pattern. V EXCELi zostrojíme multivariačný diagram ako spojnicový graf so zobrazením chybových úsečiek. Postup pri návrhu experimentu 39

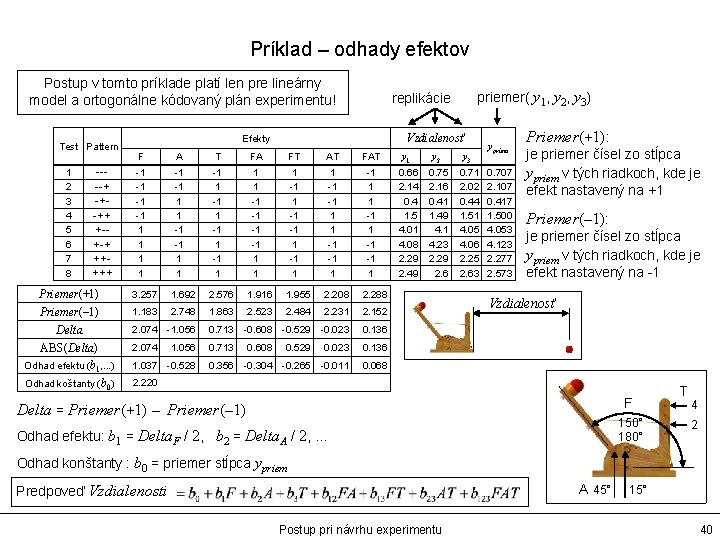
Príklad – odhady efektov Postup v tomto príklade platí len pre lineárny model a ortogonálne kódovaný plán experimentu! Test Pattern 1 2 3 4 5 6 7 8 ----+ -+-++ +-+-+ +++++ Priemer(+1) Priemer(– 1) Delta ABS(Delta) Odhad efektu (b 1, . . . ) Odhad koštanty (b 0) priemer( y 1, y 2, y 3) replikácie Vzdialenosť Efekty F A T FA FT AT FAT y 1 y 2 y 3 -1 -1 1 1 -1 1 1 1 -1 -1 1 -1 1 -1 -1 1 0. 66 2. 14 0. 4 1. 5 4. 01 4. 08 2. 29 2. 49 0. 75 2. 16 0. 41 1. 49 4. 1 4. 23 2. 29 2. 6 0. 71 2. 02 0. 44 1. 51 4. 05 4. 06 2. 25 2. 63 3. 257 1. 692 2. 576 1. 916 1. 955 2. 208 2. 288 1. 183 2. 748 1. 863 2. 523 2. 484 2. 231 2. 152 2. 074 -1. 056 0. 713 -0. 608 -0. 529 -0. 023 0. 136 2. 074 0. 713 0. 608 0. 529 0. 023 0. 136 0. 356 -0. 304 -0. 265 -0. 011 0. 068 1. 056 1. 037 -0. 528 ypriem 0. 707 2. 107 0. 417 1. 500 4. 053 4. 123 2. 277 2. 573 Priemer(+1): je priemer čísel zo stĺpca ypriem v tých riadkoch, kde je efekt nastavený na +1 Priemer(– 1): je priemer čísel zo stĺpca ypriem v tých riadkoch, kde je efekt nastavený na -1 Vzdialenosť 2. 220 F Delta = Priemer(+1) – Priemer(– 1) 150° 180° Odhad efektu: b 1 = Delta. F / 2, b 2 = Delta. A / 2, . . . T 4 2 Odhad konštanty : b 0 = priemer stĺpca ypriem A 45° Predpoveď Vzdialenosti Postup pri návrhu experimentu 15° 40

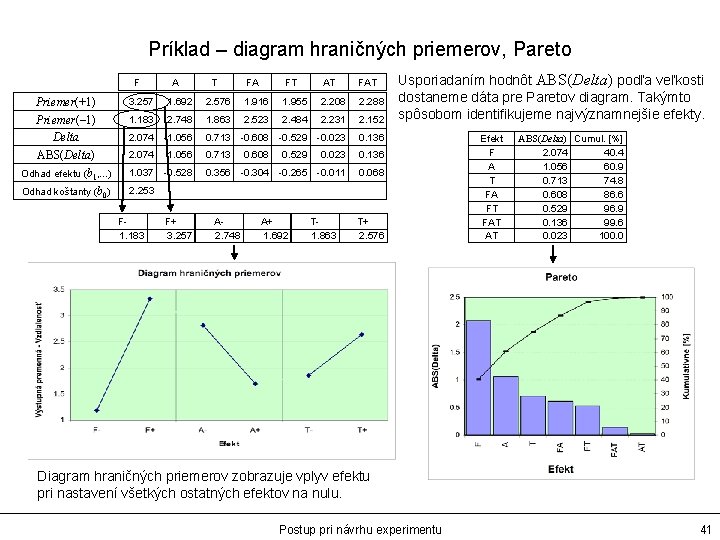
Príklad – diagram hraničných priemerov, Pareto F Priemer(+1) Priemer(– 1) Delta ABS(Delta) Odhad efektu (b 1, . . . ) Odhad koštanty (b 0) A T FA FT AT FAT 3. 257 1. 692 2. 576 1. 916 1. 955 2. 208 2. 288 1. 183 2. 748 1. 863 2. 523 2. 484 2. 231 2. 152 2. 074 -1. 056 0. 713 -0. 608 -0. 529 -0. 023 0. 136 2. 074 0. 713 0. 608 0. 529 0. 023 0. 136 0. 356 -0. 304 -0. 265 -0. 011 0. 068 1. 056 1. 037 -0. 528 Usporiadaním hodnôt ABS(Delta) podľa veľkosti dostaneme dáta pre Paretov diagram. Takýmto spôsobom identifikujeme najvýznamnejšie efekty. 2. 253 F 1. 183 F+ 3. 257 A 2. 748 A+ 1. 692 T 1. 863 T+ 2. 576 Efekt F A T FA FT FAT AT ABS(Delta) Cumul. [%] 2. 074 40. 4 1. 056 60. 9 0. 713 74. 8 0. 608 86. 6 0. 529 96. 9 0. 136 99. 6 0. 023 100. 0 Diagram hraničných priemerov zobrazuje vplyv efektu pri nastavení všetkých ostatných efektov na nulu. Postup pri návrhu experimentu 41

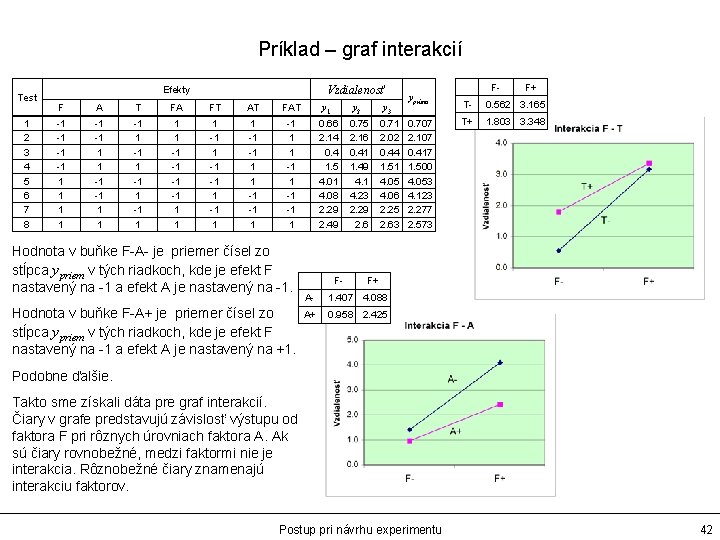
Príklad – graf interakcií Test 1 2 3 4 5 6 7 8 Vzdialenosť Efekty F A T FA FT AT FAT y 1 y 2 y 3 -1 -1 1 1 -1 1 1 1 -1 -1 1 -1 1 -1 -1 1 0. 66 2. 14 0. 4 1. 5 4. 01 4. 08 2. 29 2. 49 0. 75 2. 16 0. 41 1. 49 4. 1 4. 23 2. 29 2. 6 0. 71 2. 02 0. 44 1. 51 4. 05 4. 06 2. 25 2. 63 Hodnota v buňke F-A- je priemer čísel zo stĺpca ypriem v tých riadkoch, kde je efekt F nastavený na -1 a efekt A je nastavený na -1. Hodnota v buňke F-A+ je priemer čísel zo stĺpca ypriem v tých riadkoch, kde je efekt F nastavený na -1 a efekt A je nastavený na +1. F- ypriem 0. 707 2. 107 0. 417 1. 500 4. 053 4. 123 2. 277 2. 573 F- F+ T- 0. 562 3. 165 T+ 1. 803 3. 348 F+ A- 1. 407 4. 088 A+ 0. 958 2. 425 Podobne ďalšie. Takto sme získali dáta pre graf interakcií. Čiary v grafe predstavujú závislosť výstupu od faktora F pri rôznych úrovniach faktora A. Ak sú čiary rovnobežné, medzi faktormi nie je interakcia. Rôznobežné čiary znamenajú interakciu faktorov. Postup pri návrhu experimentu 42

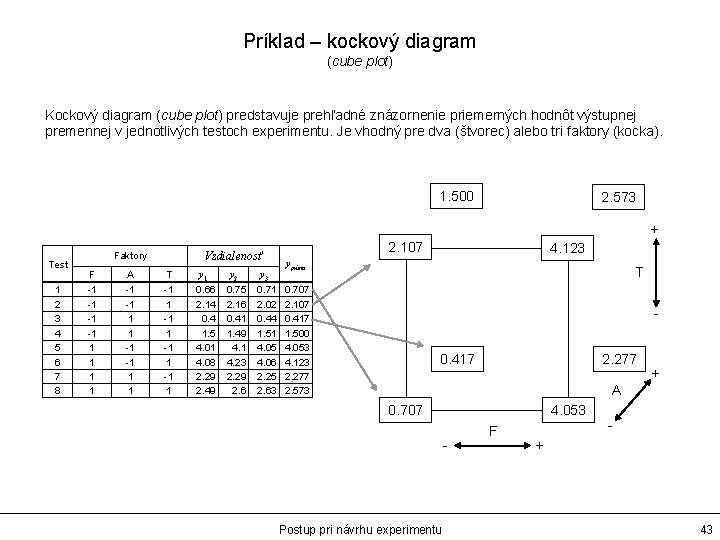
Príklad – kockový diagram (cube plot) Kockový diagram (cube plot) predstavuje prehľadné znázornenie priemerných hodnôt výstupnej premennej v jednotlivých testoch experimentu. Je vhodný pre dva (štvorec) alebo tri faktory (kocka). 1. 500 2. 573 + Test 1 2 3 4 5 6 7 8 Vzdialenosť Faktory F A T y 1 y 2 y 3 -1 -1 1 1 -1 1 0. 66 2. 14 0. 4 1. 5 4. 01 4. 08 2. 29 2. 49 0. 75 2. 16 0. 41 1. 49 4. 1 4. 23 2. 29 2. 6 0. 71 2. 02 0. 44 1. 51 4. 05 4. 06 2. 25 2. 63 2. 107 4. 123 ypriem T 0. 707 2. 107 0. 417 1. 500 4. 053 4. 123 2. 277 2. 573 0. 417 2. 277 + A 0. 707 4. 053 - Postup pri návrhu experimentu F - + 43

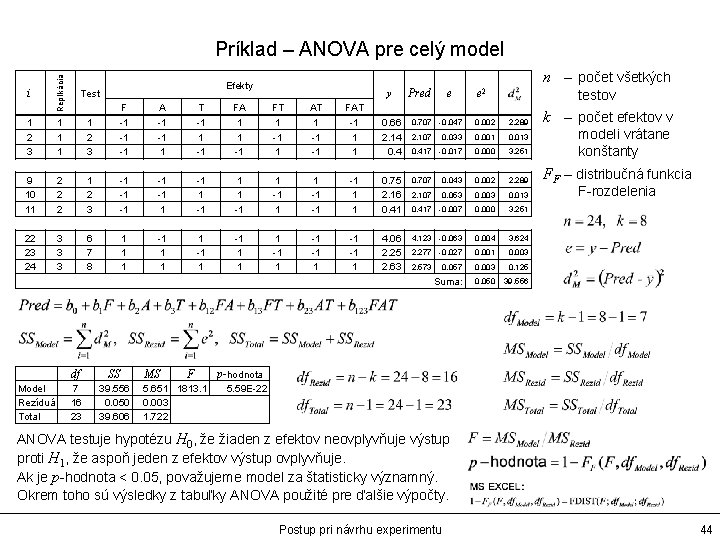
Príklad – ANOVA pre celý model Replikácia n – počet všetkých Test 1 2 3 1 1 2 3 -1 -1 -1 1 1 -1 -1 -1 1 1 0. 66 2. 14 0. 707 -0. 047 0. 002 2. 289 2. 107 0. 033 0. 001 0. 013 0. 417 -0. 017 0. 000 3. 251 9 10 11 2 2 2 1 2 3 -1 -1 -1 1 1 -1 -1 -1 1 1 0. 75 2. 16 0. 41 0. 707 0. 043 0. 002 2. 289 2. 107 0. 053 0. 003 0. 013 0. 417 -0. 007 0. 000 3. 251 22 23 24 3 3 3 6 7 8 1 1 1 -1 1 -1 -1 1 4. 06 2. 25 2. 63 4. 123 -0. 063 0. 004 3. 624 2. 277 -0. 027 0. 001 0. 003 2. 573 0. 057 0. 003 0. 125 Suma: 0. 050 39. 556 i Model Rezíduá Total Efekty y F A T FA FT AT FAT df SS 7 16 23 39. 556 0. 050 39. 606 MS F 5. 651 1813. 1 0. 003 1. 722 Pred e e 2 testov k – počet efektov v modeli vrátane konštanty FF – distribučná funkcia F-rozdelenia p-hodnota 5. 59 E-22 ANOVA testuje hypotézu H 0, že žiaden z efektov neovplyvňuje výstup proti H 1, že aspoň jeden z efektov výstup ovplyvňuje. Ak je p-hodnota < 0. 05, považujeme model za štatisticky významný. Okrem toho sú výsledky z tabuľky ANOVA použité pre ďalšie výpočty. Postup pri návrhu experimentu 44

Príklad – koeficient determinácie Model Rezíduá Total df SS 7 16 23 39. 556 0. 050 39. 606 MS F 5. 651 1813. 1 0. 003 1. 722 p-hodnota 5. 59 E-22 Koeficient determinácie je mierou tesnosti pozorovaných hodnôt k modelu. Ak R 2 = 1 znamená to, že model dokonale popisuje pozorované hodnoty. V našom prípade je R 2 = 0. 999, teda model dokáže predpovedať hodnoty veľmi blízke pozorovaniam. Upravený koeficient determinácie R 2 Adj zohľadňuje tendenciu modelu, v ktorom je veľa efektov k zvyšovaniu R 2, aj keď sú niektoré z efektov štatisticky nevýznamné. Dá sa povedať, že hodnotenie modelu pomocou je rovnako prísne pre model s jedným efektom ako pre model s desiatimi efektami. R 2 Adj hodnotí model s viacerými efektami prísnejšie. Preto je objektívnejšie hodnotenie predikčnej schopnosti modelu pomocou R 2 Adj. V našom prípade R 2 Adj = 0. 998, teda schopnosť modelu predpovedať výsledky je dobrá. Postup pri návrhu experimentu 45

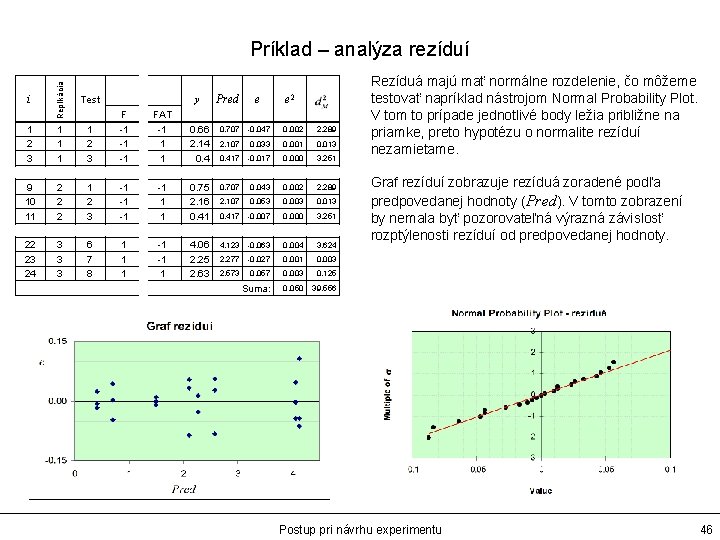
Replikácia Príklad – analýza rezíduí Test 1 2 3 1 1 2 3 -1 -1 1 1 0. 66 2. 14 0. 707 -0. 047 0. 002 2. 289 2. 107 0. 033 0. 001 0. 013 0. 417 -0. 017 0. 000 3. 251 9 10 11 2 2 2 1 2 3 -1 -1 1 1 0. 75 2. 16 0. 41 0. 707 0. 043 0. 002 2. 289 2. 107 0. 053 0. 003 0. 013 0. 417 -0. 007 0. 000 3. 251 22 23 24 3 3 3 6 7 8 1 1 1 -1 -1 1 4. 06 2. 25 2. 63 4. 123 -0. 063 0. 004 3. 624 2. 277 -0. 027 0. 001 0. 003 2. 573 0. 057 0. 003 0. 125 Suma: 0. 050 39. 556 i y F FAT Pred e e 2 Rezíduá majú mať normálne rozdelenie, čo môžeme testovať napríklad nástrojom Normal Probability Plot. V tom to prípade jednotlivé body ležia približne na priamke, preto hypotézu o normalite rezíduí nezamietame. Graf rezíduí zobrazuje rezíduá zoradené podľa predpovedanej hodnoty (Pred). V tomto zobrazení by nemala byť pozorovateľná výrazná závislosť rozptýlenosti rezíduí od predpovedanej hodnoty. Postup pri návrhu experimentu 46

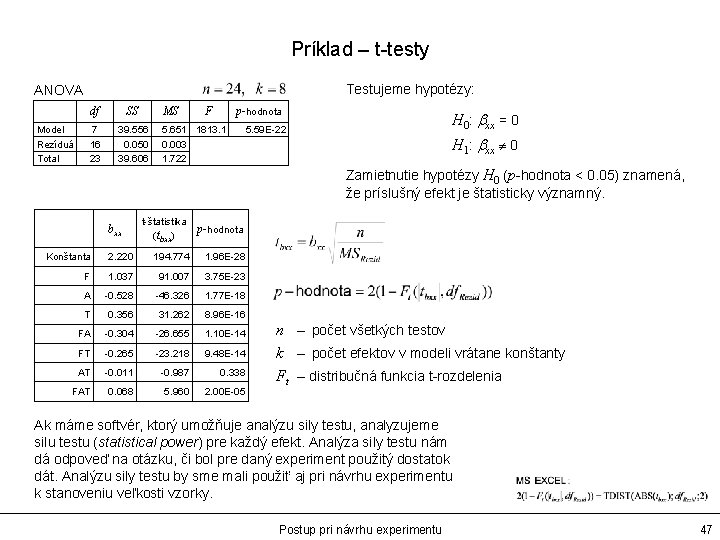
Príklad – t-testy Testujeme hypotézy: ANOVA Model Rezíduá Total df SS MS 7 16 23 39. 556 0. 050 39. 606 F p-hodnota 5. 651 1813. 1 0. 003 1. 722 H 0: bxx = 0 5. 59 E-22 H 1: bxx 0 Zamietnutie hypotézy H 0 (p-hodnota < 0. 05) znamená, že príslušný efekt je štatisticky významný. bxx t-štatistika (tbxx) p-hodnota Konštanta 2. 220 194. 774 1. 96 E-28 F 1. 037 91. 007 3. 75 E-23 A -0. 528 -46. 326 1. 77 E-18 T 0. 356 31. 262 8. 96 E-16 FA -0. 304 -26. 655 1. 10 E-14 FT -0. 265 -23. 218 9. 48 E-14 AT -0. 011 -0. 987 0. 338 FAT 0. 068 5. 960 2. 00 E-05 n – počet všetkých testov k – počet efektov v modeli vrátane konštanty Ft – distribučná funkcia t-rozdelenia Ak máme softvér, ktorý umožňuje analýzu sily testu, analyzujeme silu testu (statistical power) pre každý efekt. Analýza sily testu nám dá odpoveď na otázku, či bol pre daný experiment použitý dostatok dát. Analýzu sily testu by sme mali použiť aj pri návrhu experimentu k stanoveniu veľkosti vzorky. Postup pri návrhu experimentu 47

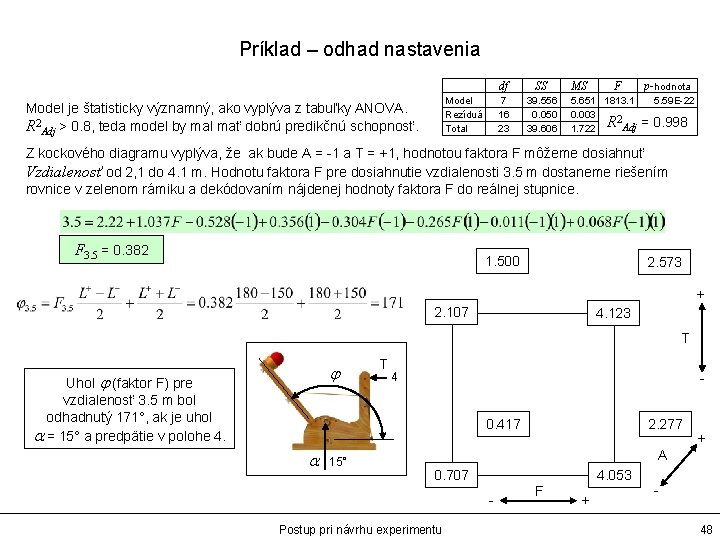
Príklad – odhad nastavenia Model Rezíduá Total Model je štatisticky významný, ako vyplýva z tabuľky ANOVA. R 2 Adj > 0. 8, teda model by mal mať dobrú predikčnú schopnosť. df SS 7 16 23 39. 556 0. 050 39. 606 MS F 5. 651 1813. 1 0. 003 2 Adj 1. 722 R p-hodnota 5. 59 E-22 = 0. 998 Z kockového diagramu vyplýva, že ak bude A = -1 a T = +1, hodnotou faktora F môžeme dosiahnuť Vzdialenosť od 2, 1 do 4. 1 m. Hodnotu faktora F pre dosiahnutie vzdialenosti 3. 5 m dostaneme riešením rovnice v zelenom rámiku a dekódovaním nájdenej hodnoty faktora F do reálnej stupnice. F 3. 5 = 0. 382 1. 500 2. 573 + 2. 107 4. 123 T j Uhol j (faktor F) pre vzdialenosť 3. 5 m bol odhadnutý 171°, ak je uhol a = 15° a predpätie v polohe 4. T - 4 0. 417 a 15° 2. 277 + A 0. 707 4. 053 - Postup pri návrhu experimentu F + 48

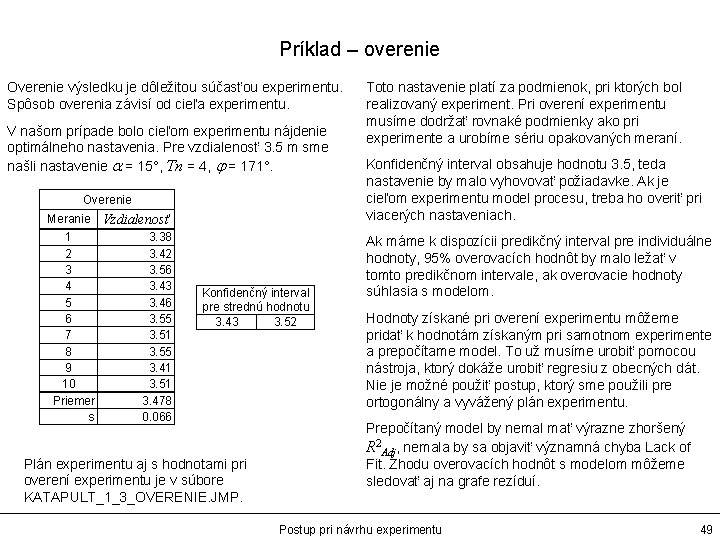
Príklad – overenie Overenie výsledku je dôležitou súčasťou experimentu. Spôsob overenia závisí od cieľa experimentu. V našom prípade bolo cieľom experimentu nájdenie optimálneho nastavenia. Pre vzdialenosť 3. 5 m sme našli nastavenie a = 15°, Tn = 4, j = 171°. Overenie Meranie Vzdialenosť 1 3. 38 2 3. 42 3 3. 56 4 3. 43 5 3. 46 6 3. 55 7 3. 51 8 3. 55 9 3. 41 10 3. 51 Priemer 3. 478 s 0. 066 Konfidenčný interval pre strednú hodnotu 3. 43 3. 52 Plán experimentu aj s hodnotami pri overení experimentu je v súbore KATAPULT_1_3_OVERENIE. JMP. Toto nastavenie platí za podmienok, pri ktorých bol realizovaný experiment. Pri overení experimentu musíme dodržať rovnaké podmienky ako pri experimente a urobíme sériu opakovaných meraní. Konfidenčný interval obsahuje hodnotu 3. 5, teda nastavenie by malo vyhovovať požiadavke. Ak je cieľom experimentu model procesu, treba ho overiť pri viacerých nastaveniach. Ak máme k dispozícii predikčný interval pre individuálne hodnoty, 95% overovacích hodnôt by malo ležať v tomto predikčnom intervale, ak overovacie hodnoty súhlasia s modelom. Hodnoty získané pri overení experimentu môžeme pridať k hodnotám získaným pri samotnom experimente a prepočítame model. To už musíme urobiť pomocou nástroja, ktorý dokáže urobiť regresiu z obecných dát. Nie je možné použiť postup, ktorý sme použili pre ortogonálny a vyvážený plán experimentu. Prepočítaný model by nemal mať výrazne zhoršený R 2 Adj, nemala by sa objaviť významná chyba Lack of Fit. Zhodu overovacích hodnôt s modelom môžeme sledovať aj na grafe rezíduí. Postup pri návrhu experimentu 49

Použitá a doporučená literatúra a softvér 1. The Certified Six Sigma Black Belt Primer, First Edition, Quality Council of Indiana, December 2001, 2. T. P. Ryan, Statistical Methods for Quality Improvement, JOHN WILEY & SONS, New York, 1989 3. Štatistika – slovník a značky, časť 3: Navrhovanie experimentov, Slovenská technická norma STN ISO 3534 -3, jún 1993 4. S. R. Schmidt, R. G. Launsby, Understanding Industrial Designed Experiments, AIR ACADEMY PRESS, Colorado Springs, 1994 5. A. J. Duncan, Quality Control and Industrial Statistics, Richard D. Irwin, Inc. , Fifth Edition, 1986 6. T. H. Wonnacot, R. J. Wonnacot, Statistika pro obchod a hospodářství, VICTORIA PUBLISHING a. s. , Praha, 1993 7. Microsoft® EXCEL, Microsoft Corporation 8. JMP , The Statistical Discovery Software , SAS Institute Inc. , version 3. 2 – 5. 012 Postup pri návrhu experimentu 50