DESIGN OF EXPERIMENT DOE OVERVIEW Dedy Sugiarto Slide

DESIGN OF EXPERIMENT (DOE) OVERVIEW Dedy Sugiarto Slide 1

n DOE is a methodology for systematically applying statistics to experimentation (Lye, 2005). n There are many types of DOE techniques that include single factor experiment, general full factorial, two-level full factorial, fractional factorial, response surface designs, mixture designs and taguchi designs. Slide 2

n An experiment is a test or series of tests in which purposeful changes are made to the input variables of a process or system so that we may observe and identify the reasons for changes that may be observed in the output response (Montgomery 2005) ] Slide 3

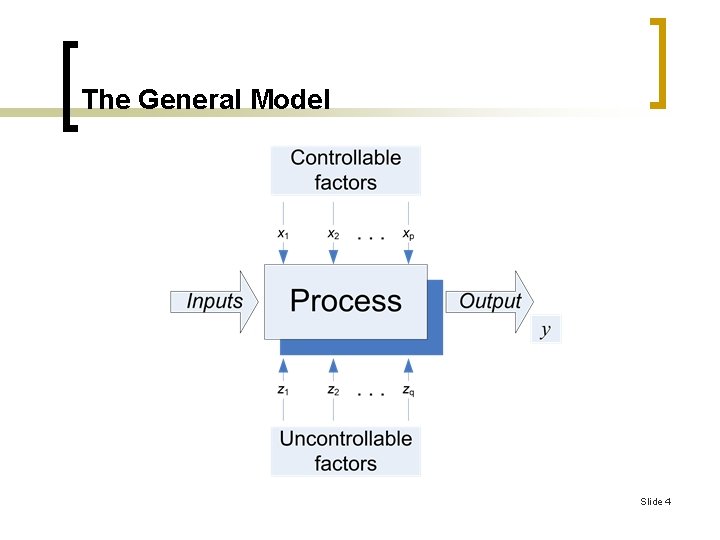
The General Model Slide 4

Examples of simple experiments No Response or output Factors or input variables 1 taste (maximize), un- brand, time, power popped kernels (minimize) of microwave popcorns 2 virus scan time RAM cache, program size, operating system 3 time to boil water pan type, burner size, cover, amount of water, lid on or off, size of pan Slide 5

No Response Factors 4 distance paper aeroplane flew design, paper weight, angle 5 blending time for soy beans blending speed, amount of water, temperature of water, soaking time before blending 6 height of cake oven temperature, length of heating, amount of water 7 length of rubber band before it broke brand of rubber band, size, temperature Slide 6

Introduction n n We can usually visualize the process as a combination of machines, methods, people, and other resources that transform some input (often a material) into an output that has one or more observable responses. Some of the process variables x 1, x 2, …, xp are controllable. Slide 7

Introduction n n Whereas other variables z 1, z 2, …, zq are uncontrollable (although they may be controllable for purposes of a test). The objectives of the experiment may include the following: ¡ Determining which variables are most influential on the response y. Slide 8

Objectives of Experiment ¡ ¡ ¡ Determining where to set the influential x’s so that y is almost always near the desired nominal value. Determining where to set the influential x’s so that variability in y is small. Determining where to set the influential x’s so that the effects of the uncontrollable variables z 1, z 2, …, zq are minimized. Slide 9

Basic Principles n n In order to perform the experiment most efficiently, a scientific approach to planning the experiment must be employed. Statistical design of experiments refers to the process of planning the experiment so that appropriate data that can be analyzed by statistical methods will be collected, resulting in valid and objective conclusions. Slide 10

Basic Principles n n Thus, there are two aspects to any experimental problem: the design of the experiment and the statistical analysis of the data. The three basic principles of experimental design are: ¡ Replication: The repetition of the basic experiment. Slide 11

Introduction (Basic Principles) ¡ ¡ Randomization: Randomly determination of the experiment. Blocking: The assumption of homogeneous conditions. Slide 12

Introduction (Replication) n Replication has two important properties. ¡ First, it allows the experimenter to obtain an estimate of the experimental error. This estimate of error becomes a basic unit of measurement for determining whether the observed differences in the data are really statistically different. Slide 13

Introduction (Replication) ¡ n Second, if the sample mean is used to estimate the effect of a factor in the experiment, replication permits the experimenter to obtain a more precise estimate of this effect. There is an important distinction between replication and repeated measurements! Replication reflects sources of variability both between runs and (potentially) within runs. Slide 14

Introduction (Randomization) n n By randomization we mean that both the allocation of the experimental material and the order in which the individual runs or trials of the experiment to be performed are randomly determined. Statistical methods require that the observations (or errors) be independently distributed random variables. Slide 15

Introduction (Randomization) n n Randomization usually makes this assumption valid! By properly randomizing the experiment, we also assist in “averaging out” the effects of extraneous factors that may be present. Slide 16

Introduction n n (Blocking) Blocking is a design technique used to improve the precision with which comparisons among the factors of interest are made. Often blocking is used to reduce or eliminate the variability transmitted from nuisance factors. Generally, a block is a set of relatively homogeneous experimental conditions! Slide 17

Fixed or Random Factors ? Fixed Factor n we wish to test hypotheses about the treatment means, and our conclusion will apply only to the factor levels considered in the analysis Ho : 1 = 2 = …. = a H 1 : i ≠ j for at least one pair (i, j) Slide 18

Experiments with fixed factors Example : n Popcorn experiment 0 bjective : To investigate the influence of pop corn brands on the proportion of unpopped kernels (minimize). Slide 19

Random Factor n We wish to test hyphotesis about the variability and try to estimate this variability n We are able to extend the conclusions (which are based on the sample of treatments) to all treatments in the populations Slide 20

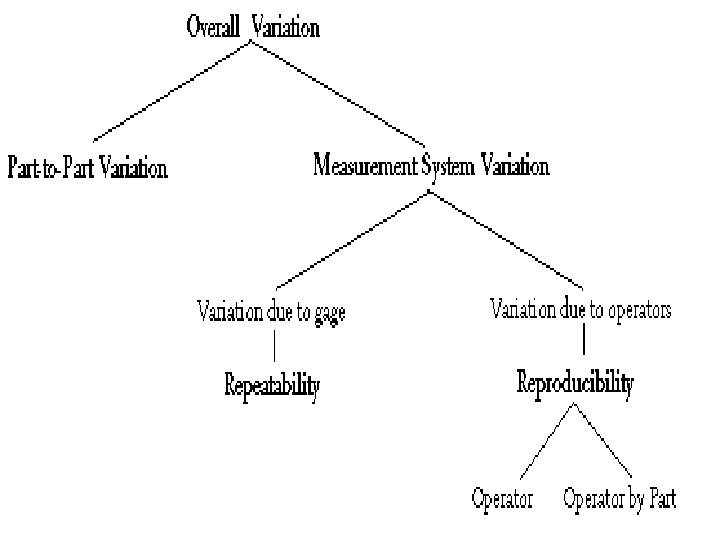
Experiments with random factors Example : n Measurement System Analysis 0 bjective : determine how much of your observed process variation is due to measurement system variation. Slide 21

Slide 22

The Guidelines n An outline of the recommended procedure is as follows: ¡ ¡ Recognition of and statement of the problem. Selection of the response variable. Choice of factors, levels, and ranges. Choice of experimental design. Slide 23

Introduction (The Guidelines) ¡ ¡ ¡ Performing the experiment. Statistical analysis of the data. Conclusions and recommendations. Slide 24

Example of single factor experiment with qualitative factor (Popcorn experiment) n For example, we may want to investigate the influence of pop corn brands on the proportion of un-popped kernels (minimize). We use completely randomize design or without blocking of experimental unit for this single factor experiment. There are tree levels for brand (A, B and C) and tree replications for each lavel. We use one hundred kernels for each trial and 3, 5 minutes to make pop corn on stove. Slide 25

n We wish to test hypotheses about the treatment means, and our conclusion will apply only to the factor levels considered in the analysis Ho : 1 = 2 = …. = a H 1 : i ≠ j for at least one pair (i, j) Slide 26

Randomization using Minitab : Run order Un-popped kernels proportion Brand C Brand B Brand A Brand B Slide 27

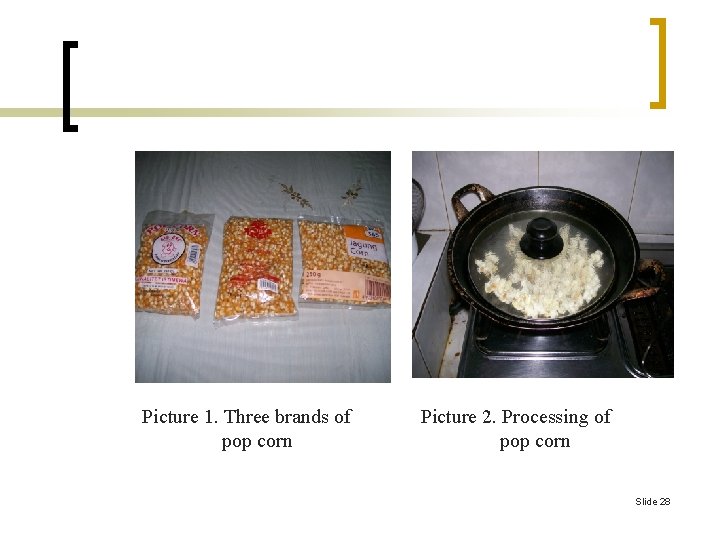
Picture 1. Three brands of pop corn Picture 2. Processing of pop corn Slide 28

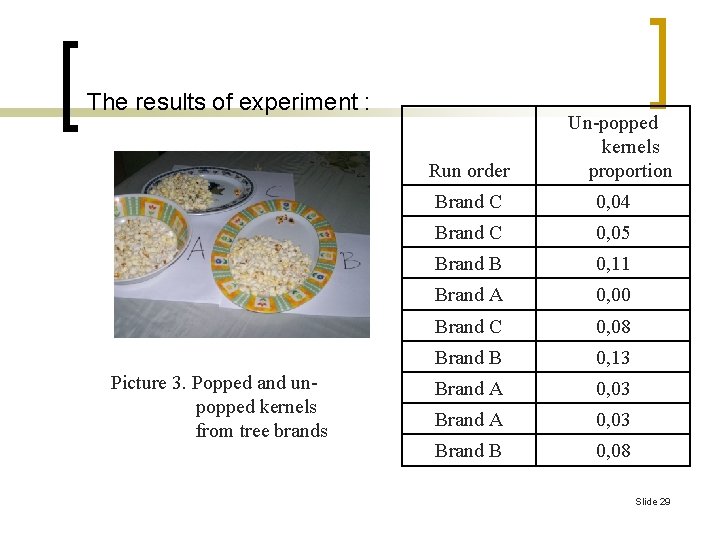
The results of experiment : Run order Picture 3. Popped and unpopped kernels from tree brands Un-popped kernels proportion Brand C 0, 04 Brand C 0, 05 Brand B 0, 11 Brand A 0, 00 Brand C 0, 08 Brand B 0, 13 Brand A 0, 03 Brand B 0, 08 Slide 29

Minitab Output : One-way ANOVA: Pooled St. Dev = 0, 02134 Source DF SS MS F P Brand 2 0, 011356 0, 005678 12, 46 0, 007 Error 6 0, 002733 0, 000456 Total 8 0, 014089 S = 0, 02134 R-Sq = 80, 60% R-Sq(adj) = 74, 13% Level Brand A Brand B Brand C N 3 3 3 Mean 0, 02000 0, 10667 0, 05667 St. Dev 0, 01732 0, 02517 0, 02082 Individual 95% CIs For Mean Based on Pooled St. Dev ---+---------+-----+-----(-------*-------) (-------*------) (------*-------) ---+---------+-----+-----0, 000 0, 040 0, 080 0, 120 Slide 30

Interpreting the Results : n The small p-values for the brand (p = 0. 007) that lower than α ( 0. 05) suggest there is significant effect of brand on proportion of un-popped kernels. Individual 95% confidence interval for mean of three brand suggest that brand A has significantly difference with brand B. Slide 31

Example of single factor experiment with quantitative factor (Cotton experiment) n n A product development engineer is interested in investigating the tensile strength of a new synthetic fiber that will be used to make cloth for men’s shirts. The engineer knows from previous experience that the strength is affected by the weight percent of cotton used in the blend of materials for the fiber. Slide 32

The Example n n Furthermore, she suspects that increasing the cotton content will increase the strength, at least initially. She also knows that cotton content should range between about 10 and 40 percent if the final product is to have other quality characteristics that are desired (such as the ability to take a permanent-press finishing treatment). Slide 33

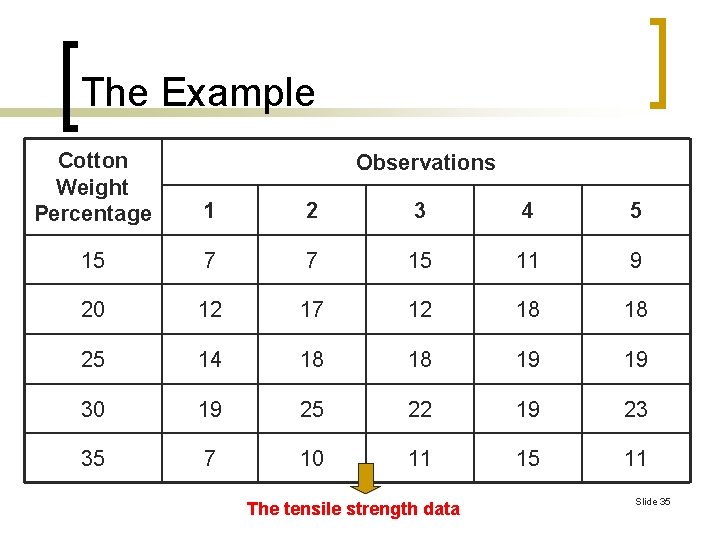
The Example n n The engineer decides to test specimens at five levels of cotton weight percent: 15, 20, 25, 30, and 35 percent. She also decides to test five specimens at each level of cotton content. This is a single-factor experiment with a = 5 levels of the factor and n = 5 replicates. The 25 runs should be made in random order. Slide 34

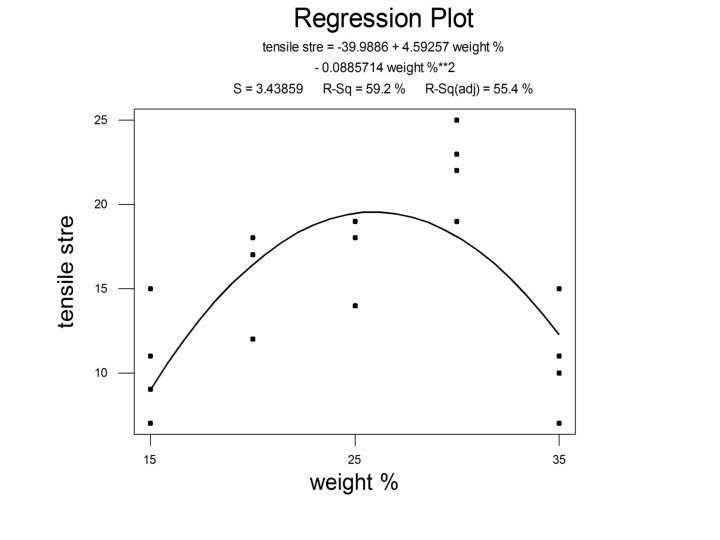
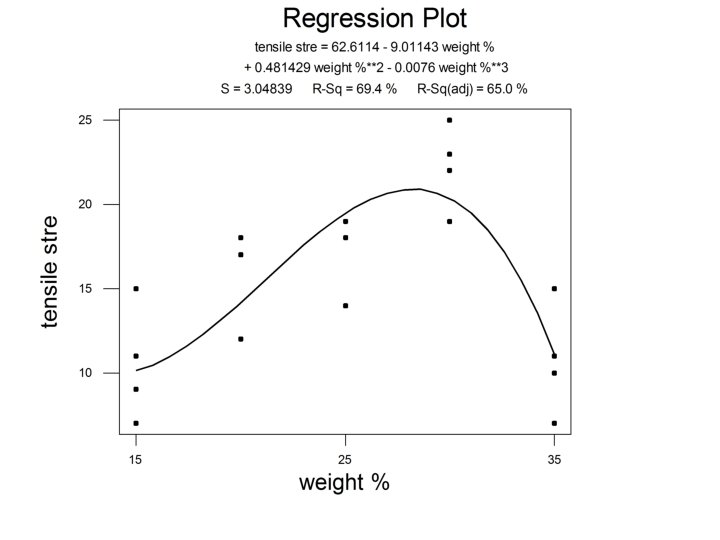
The Example Cotton Weight Percentage 1 2 3 4 5 15 7 7 15 11 9 20 12 17 12 18 18 25 14 18 18 19 19 30 19 25 22 19 23 35 7 10 11 15 11 Observations The tensile strength data Slide 35

Slide 36

Slide 37