Multiplication with Vectors Scalar Multiplication Dot Product Cross


















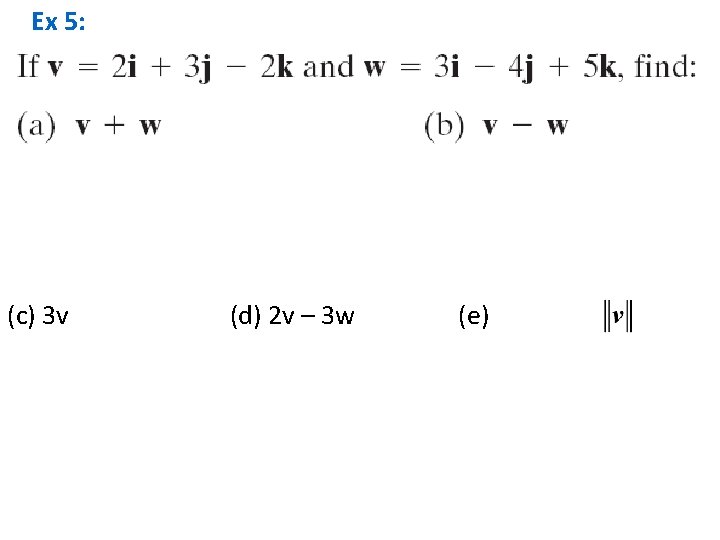
























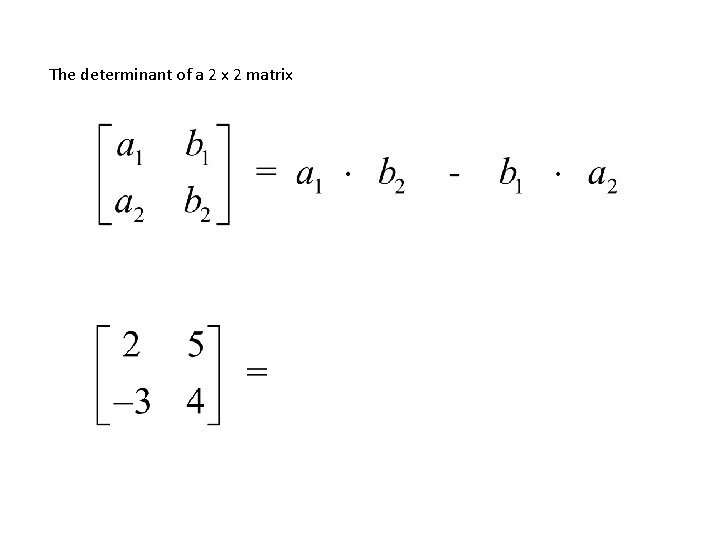




- Slides: 61

Multiplication with Vectors Scalar Multiplication Dot Product Cross Product

Objectives • TSW use the dot product to fin the relationship between two vectors. • TSWBAT determine if two vectors are perpendicular

A bit of review • A vector is a _________ • The sum of two or more vectors is called the __________ • The length of a vector is the _______

Find the sum • Vector a = < 3, 9 > and vector b = < -1, 6 > • Find • What is the magnitude of the resultant. • Hint* remember use the distance formula.

Multiplication with Vectors Scalar Multiplication Dot Product Cross Product

Scalar Multiplication: returns a vector answer Distributive Property:

Multiplication with Vectors Scalar Multiplication Dot Product Cross Product

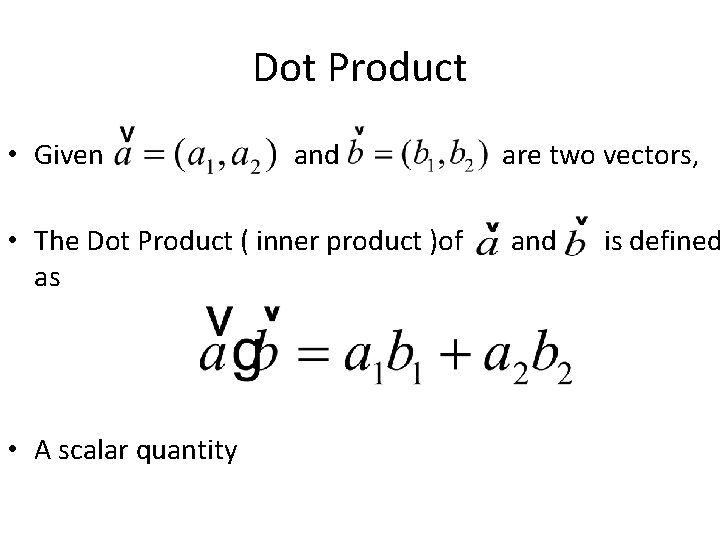
Dot Product • Given and • The Dot Product ( inner product )of as • A scalar quantity are two vectors, and is defined

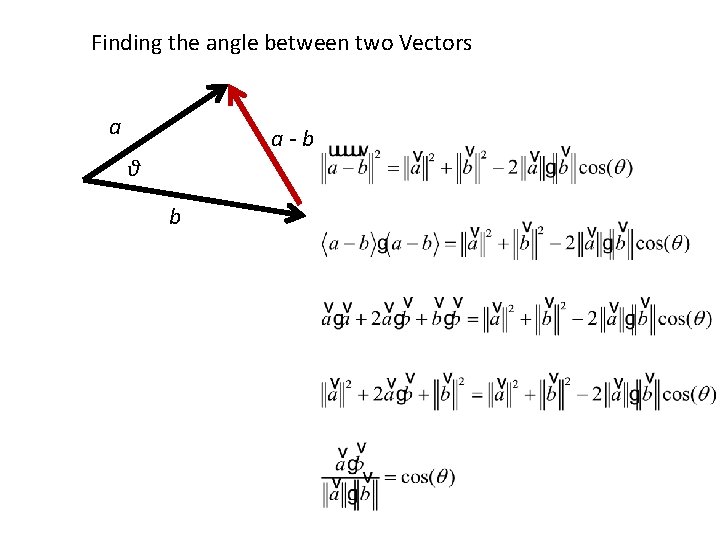
Finding the angle between two Vectors a a-b θ b

Example • Find the angle between the vectors:

1:


2:



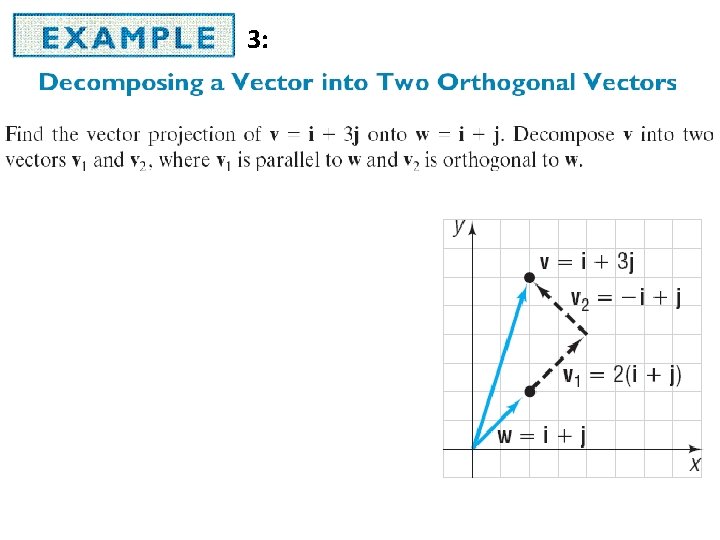
3:

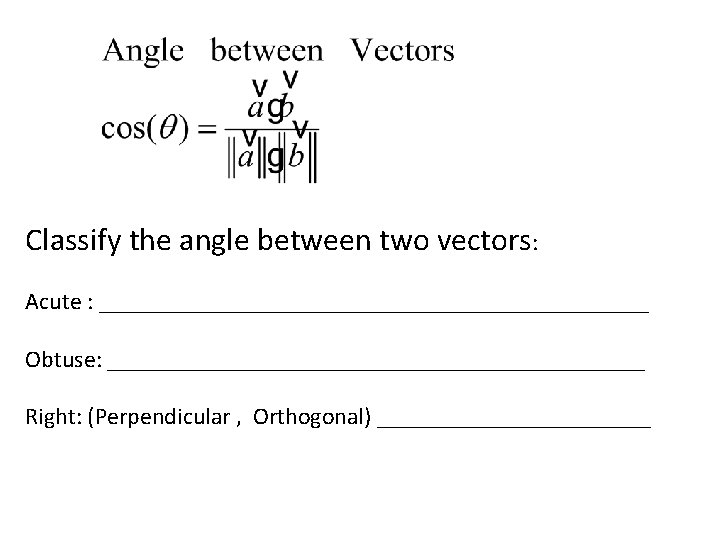
Classify the angle between two vectors: Acute : _______________________ Obtuse: _______________________ Right: (Perpendicular , Orthogonal) ____________

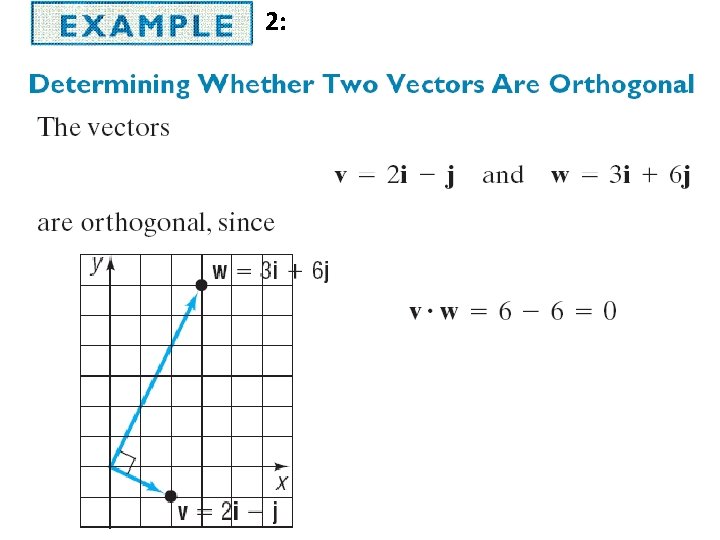
example THEOREM: Two vectors are perpendicular iff their Dot (inner) product is zero. • Given three vectors determine if any pair is perpendicular



Ex 1:


Ex 2:


Ex 3: Find the unit vector in the same direction as v = 2 i-3 j-6 k

Ex 4: Find: If v = 2 i - 3 j + 6 k and w = 5 i + 3 j – k
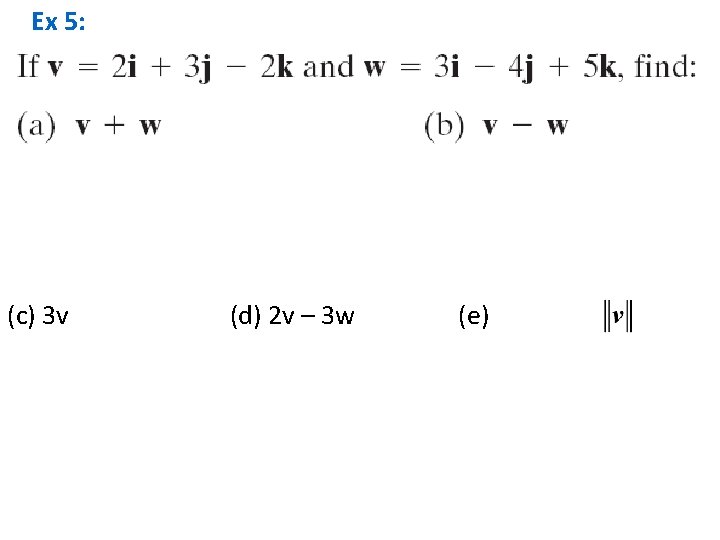
Ex 5: (c) 3 v (d) 2 v – 3 w (e)


Ex 6: Find the angle between u = 2 i -3 j + 6 k and v = 2 i + 5 j - k



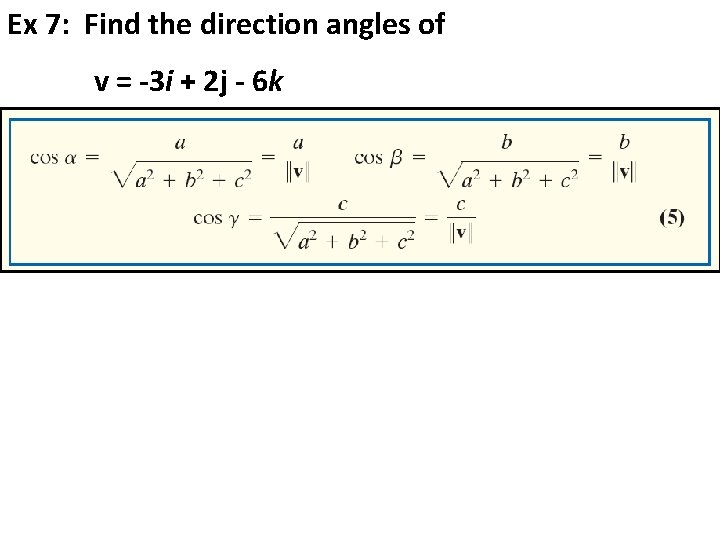
Ex 7: Find the direction angles of v = -3 i + 2 j - 6 k


Any nonzero vector v in space can be written in terms of its magnitude and direction cosines as: Ex 9: Find the direction angles of the vector below. Write the answer in the form of an equation. v = 3 i – 5 j + 2 k

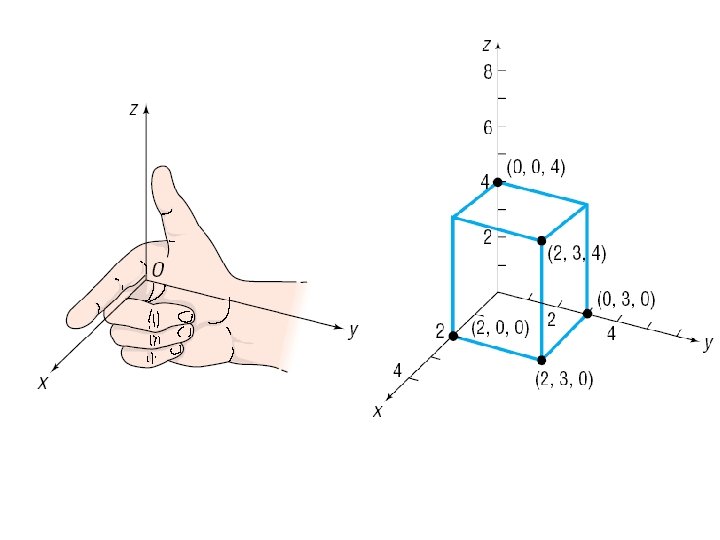
• We can also find the Dot Product of two vectors in 3 -d space. • Two vectors in space are perpendicular iff their inner product is zero.

Example • Find the Dot Product of vector v and w. • Classify the angle between the vectors.

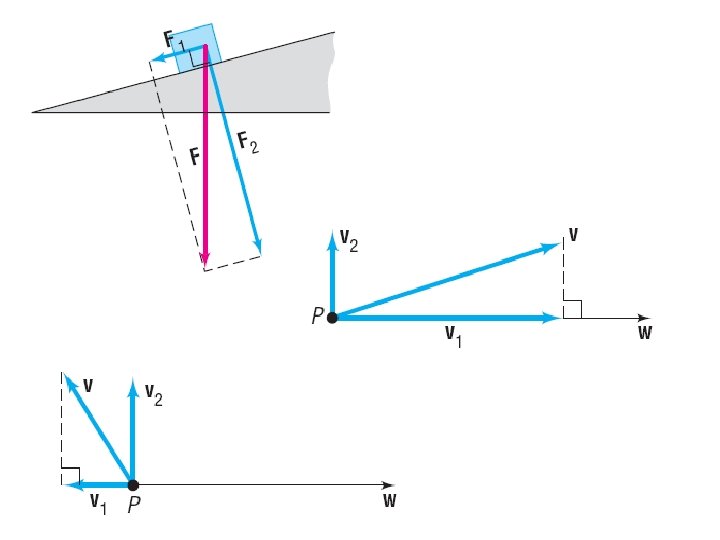
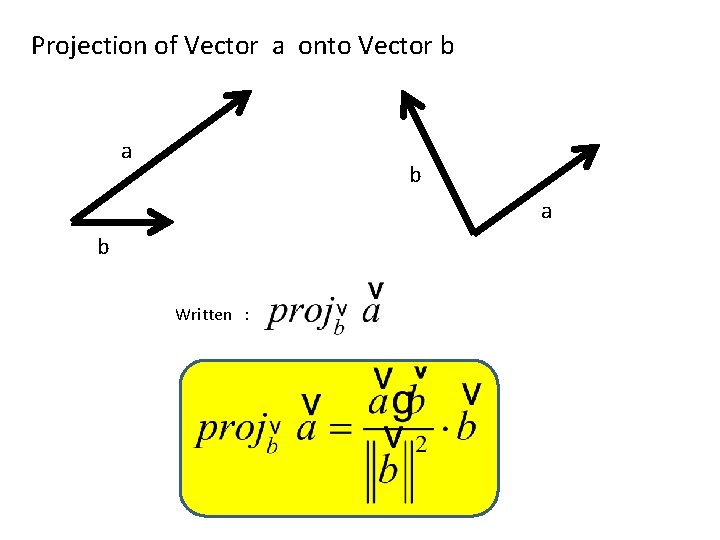
Projection of Vector a onto Vector b a b Written :

Example: Find the projection of vector a onto vector b :

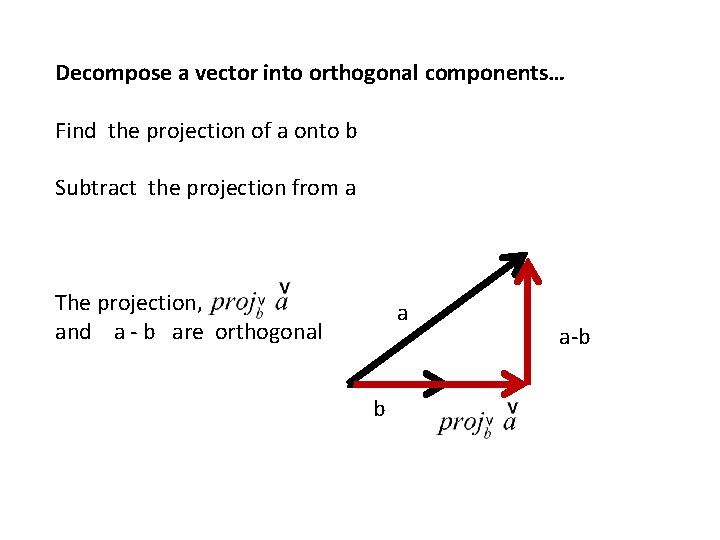
Decompose a vector into orthogonal components… Find the projection of a onto b Subtract the projection from a The projection, and a - b are orthogonal a b a-b

Multiplication with Vectors Scalar Multiplication Dot Product Cross Product

OBJECTIVE 1




OBJECTIVE 2


OBJECTIVE 3


OBJECTIVE 4




OBJECTIVE 5


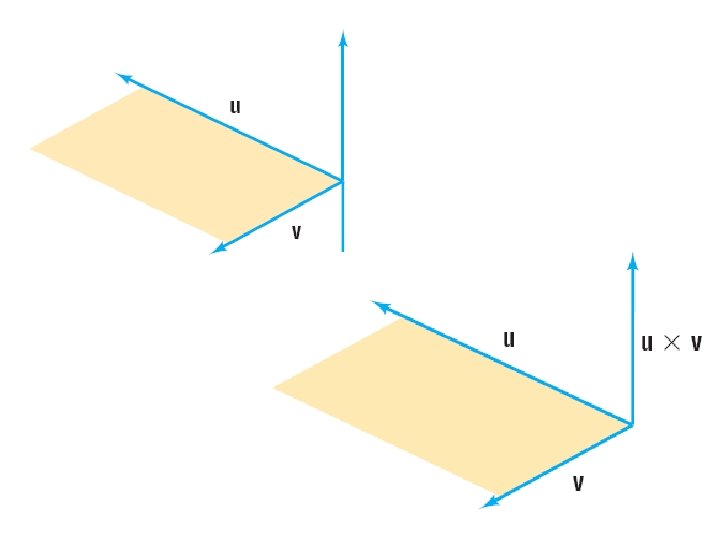
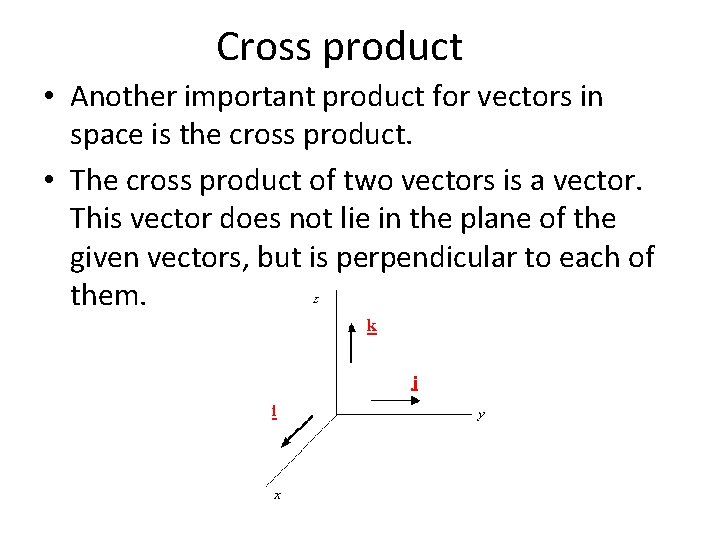
Cross product • Another important product for vectors in space is the cross product. • The cross product of two vectors is a vector. This vector does not lie in the plane of the given vectors, but is perpendicular to each of them.

• If Then the cross product of vector a and vector b is defined as follows:
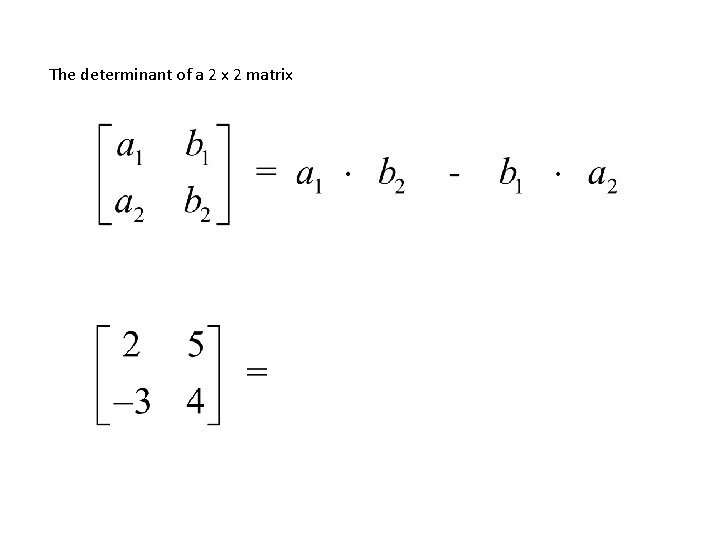
The determinant of a 2 x 2 matrix

• An easy way to remember the coefficients of vectors I, j, and k is to set up a determinant as shown and expand by minors using the first row. You can check your answer by using the dot product.

Example • Find the cross product of vector a and vector b if: Verify that your answer is correct.


Assignment