Examples of Vector Quantities Scalar Multiple of a

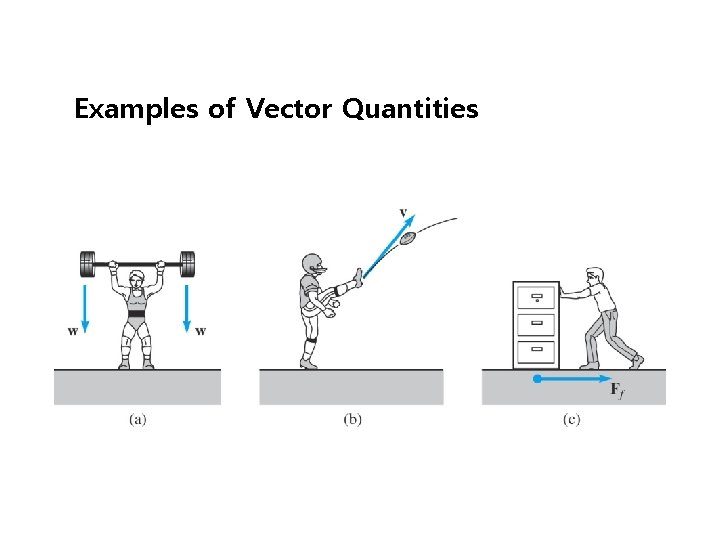
Examples of Vector Quantities

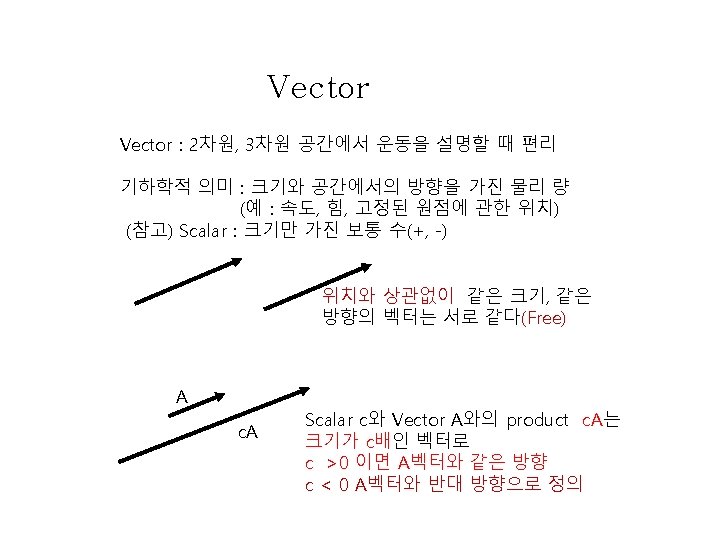
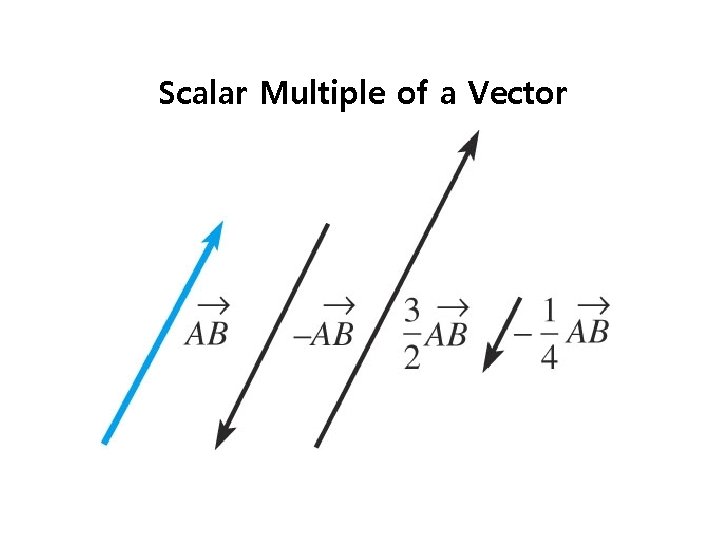
Scalar Multiple of a Vector

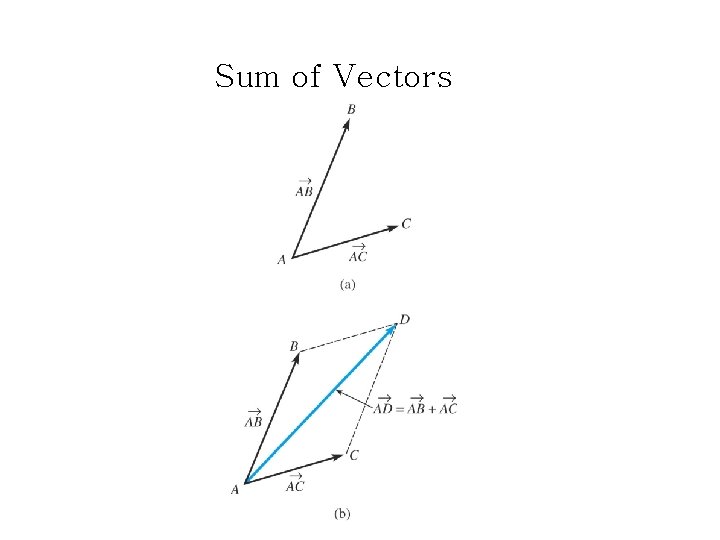
Sum of Vectors

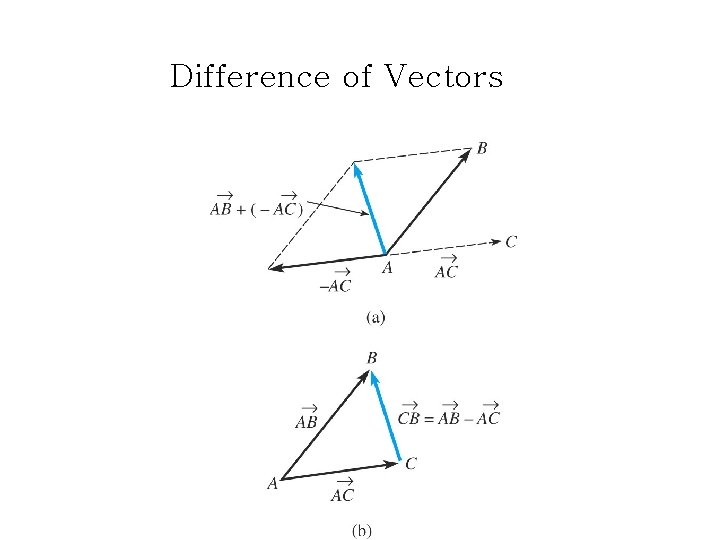
Difference of Vectors

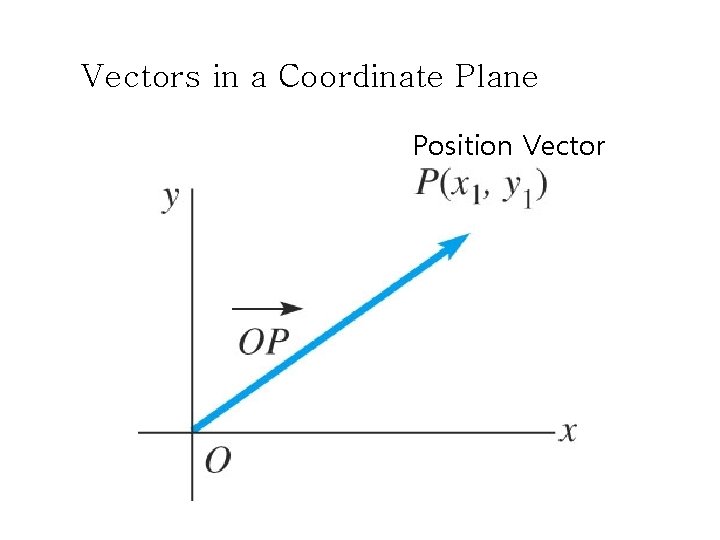
Vectors in a Coordinate Plane Position Vector

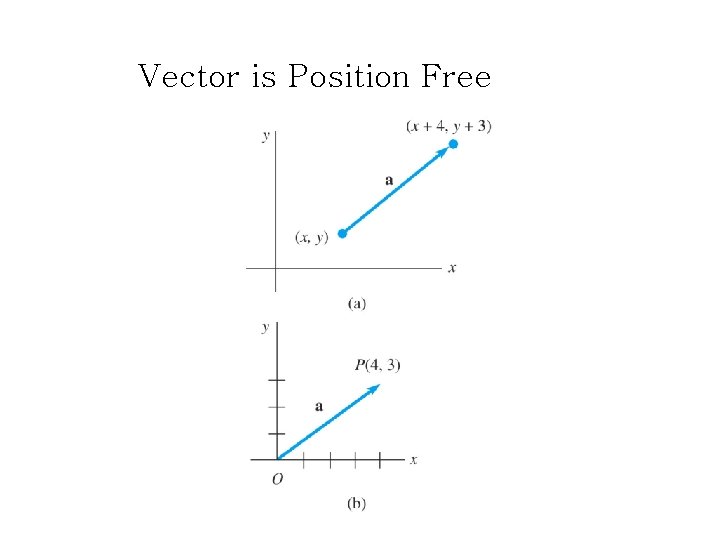
Vector is Position Free

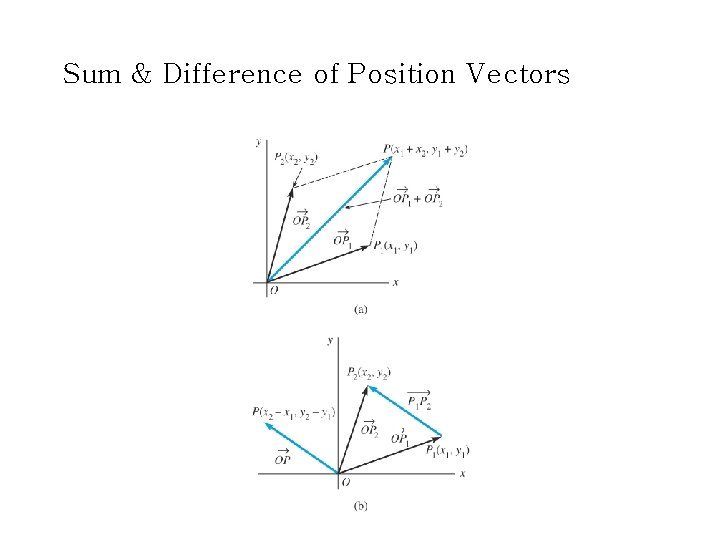
Sum & Difference of Position Vectors

Definition a = (a 1, a 2) , b = (b 1, b 2) 1) Addition a + b = (a 1+b 1, a 2+b 2) 2) Scalar Multiplication ka = (ka 1, ka 2) 3) Equality a = b if & only if a 1 = b 1, a 2 = b 2

Properties of Vectors 1. 2. 3. 4. 5. 6. 7. 8. 9. a+b=b+a (Commutative Law) a + (b + c ) = (a + b) + c (Associative Law) a+0=a (Additive Identity) a + (-a) = 0 (Additive Inverse) k(a+b) = ka + kb k : scalar (k 1 + k 2)a = k 1 a + k 2 a k 1(k 2 a) = (k 1 k 2)a 1 a = a 0 a = 0 (Zero Vector)

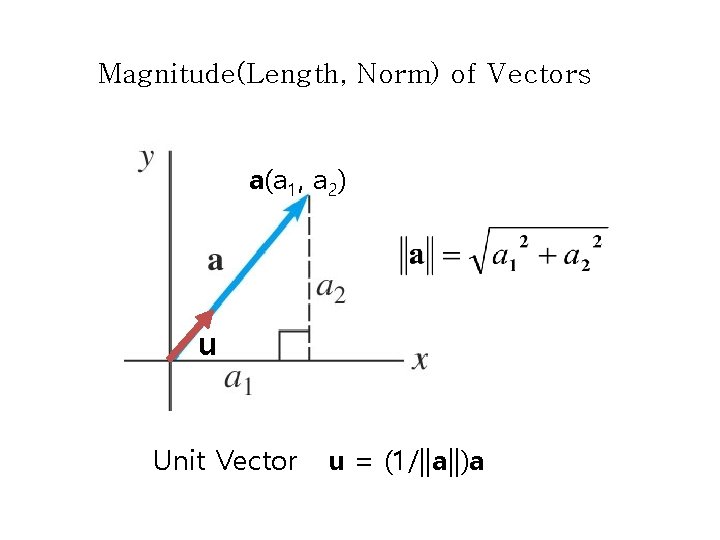
Magnitude(Length, Norm) of Vectors a(a 1, a 2) u Unit Vector u = (1/||a||)a

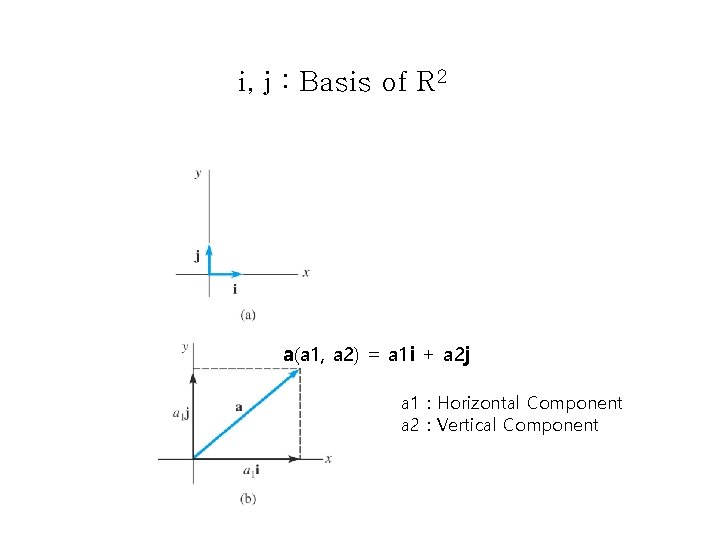
i, j : Basis of R 2 a(a 1, a 2) = a 1 i + a 2 j a 1 : Horizontal Component a 2 : Vertical Component

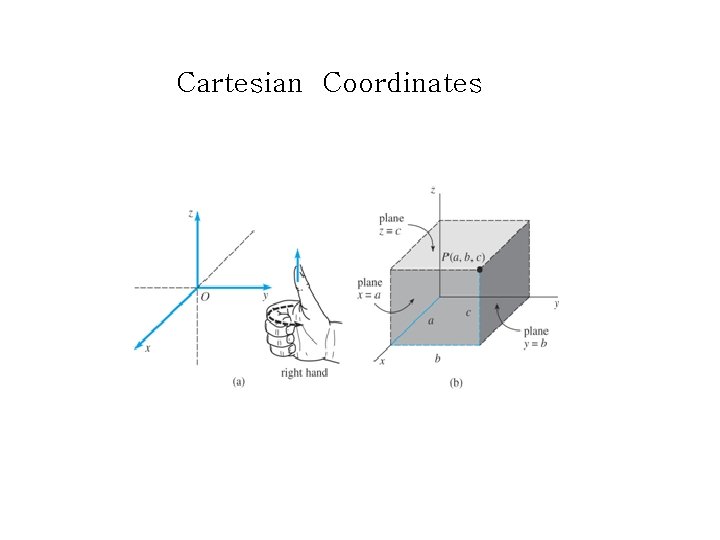
Cartesian Coordinates

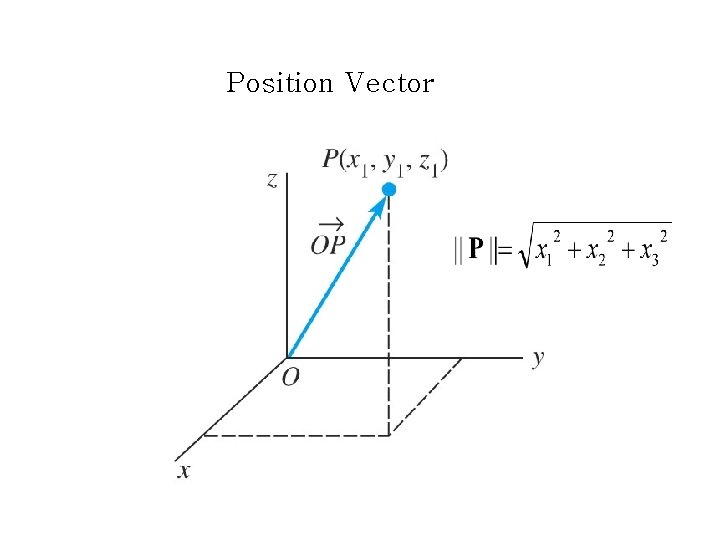
Position Vector

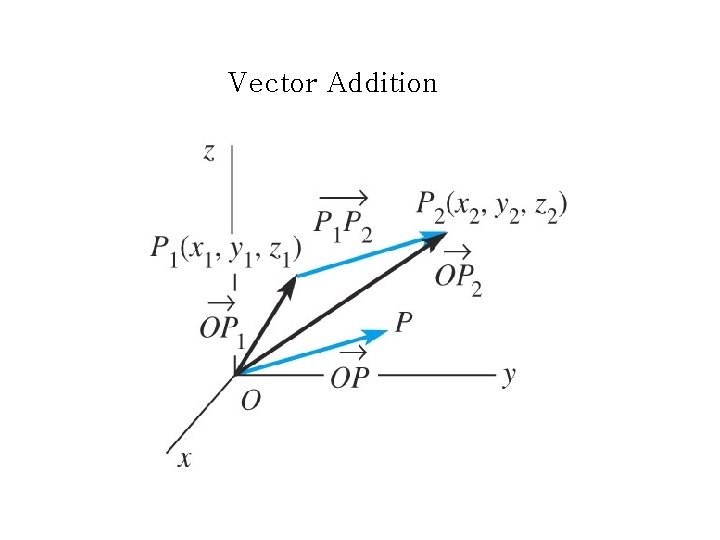
Vector Addition

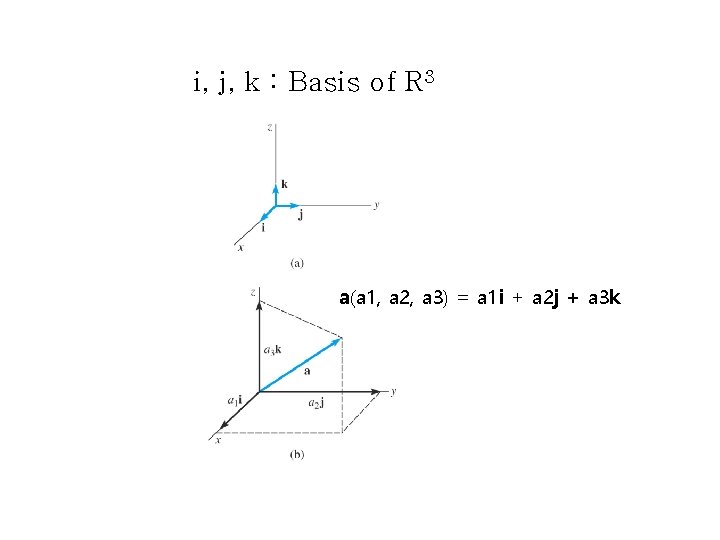
i, j, k : Basis of R 3 a(a 1, a 2, a 3) = a 1 i + a 2 j + a 3 k

Definition a = (a 1, a 2, a 3) , b = (b 1, b 2, b 3) 1) Addition a + b = (a 1+b 1, a 2+b 2, a 3+b 3) 2) Scalar Multiplication ka = (ka 1, ka 2, ka 3) 3) Equality a = b if & only if a 1 = b 1, a 2 = b 2, a 3=b 3 4) Negative -b = (-b 1, -b 2, -b 3) 5) Subtraction a-b = a + (-b) = (a 1 -b 1, a 2 -b 2, a 3 -b 3) 6) Zero Vector 0 =(0, 0, 0) 7) Magnitude

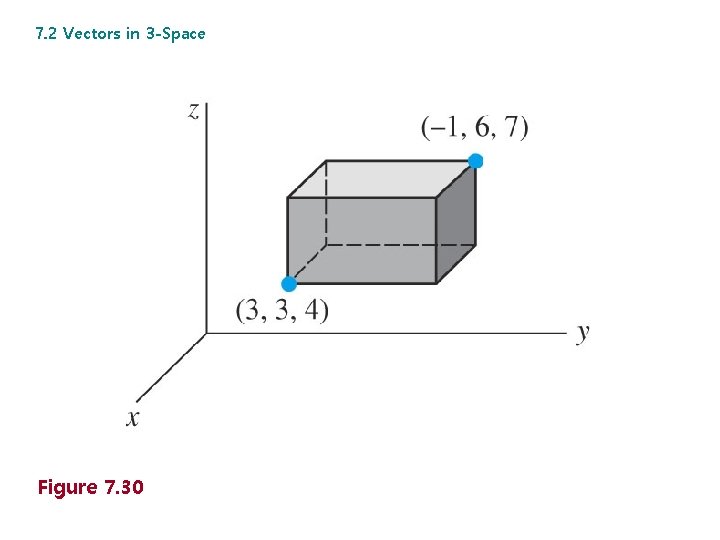
7. 2 Vectors in 3 -Space Figure 7. 30

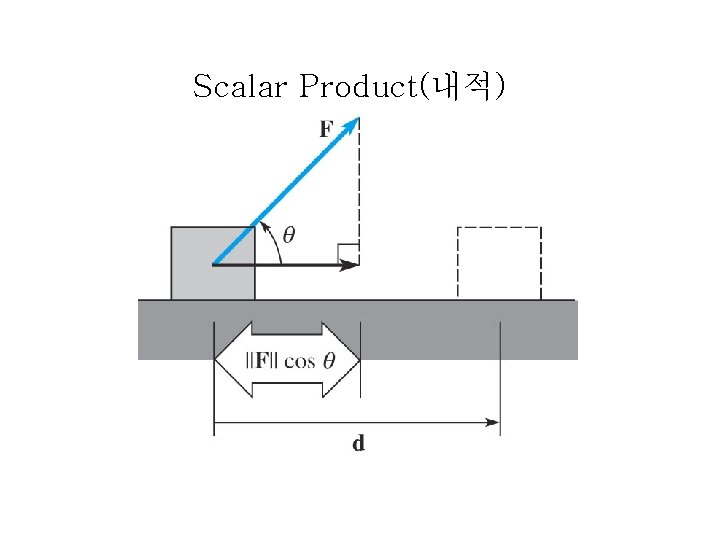
Scalar Product(내적)

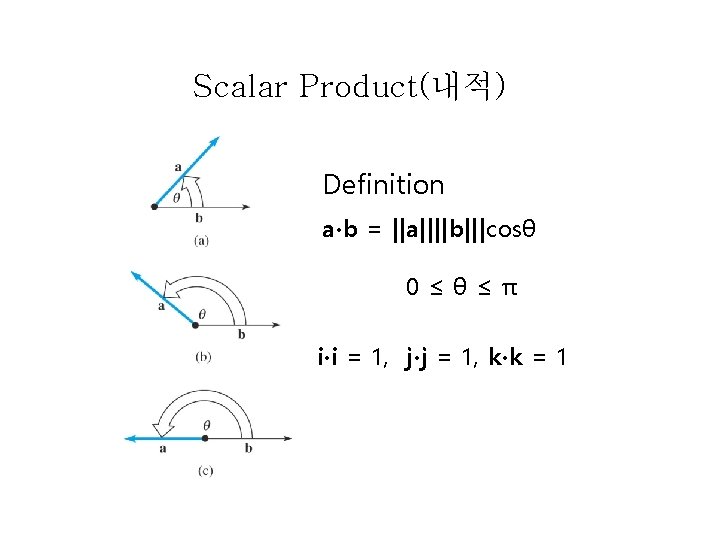
Scalar Product(내적) Definition a∙b = ||a||||b|||cosθ 0≤θ≤π i∙i = 1, j∙j = 1, k∙k = 1

Scalar Product(내적) Properties of the Scalar Product 1. a∙b = 0 if a = 0 of b = 0 2. a∙b = b∙a (Commutative Law) 3. a∙(b + c) = a∙b + a∙c (Distributive Law) 4. a∙(kb) = (ka)∙b = k(a∙b) k : Scalar 5. a∙a ≥ 0 6. a∙a = ||a||2

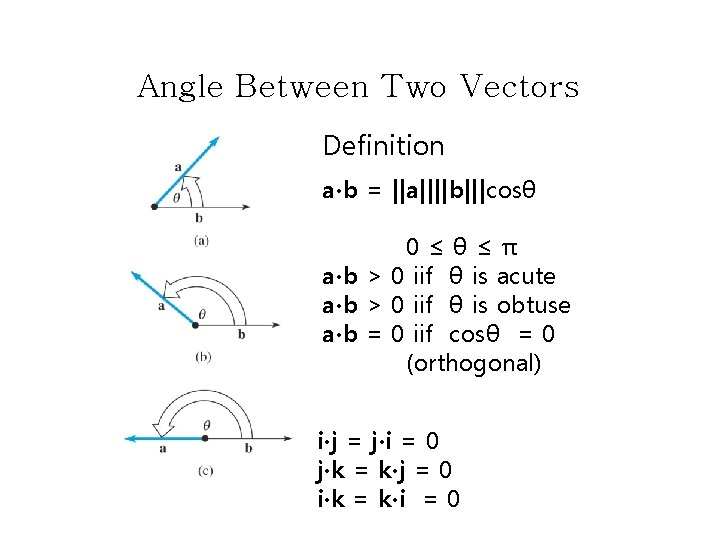
Angle Between Two Vectors Definition a∙b = ||a||||b|||cosθ 0≤θ≤π a∙b > 0 iif θ is acute a∙b > 0 iif θ is obtuse a∙b = 0 iif cosθ = 0 (orthogonal) i∙j = j∙i = 0 j∙k = k∙j = 0 i∙k = k∙i = 0

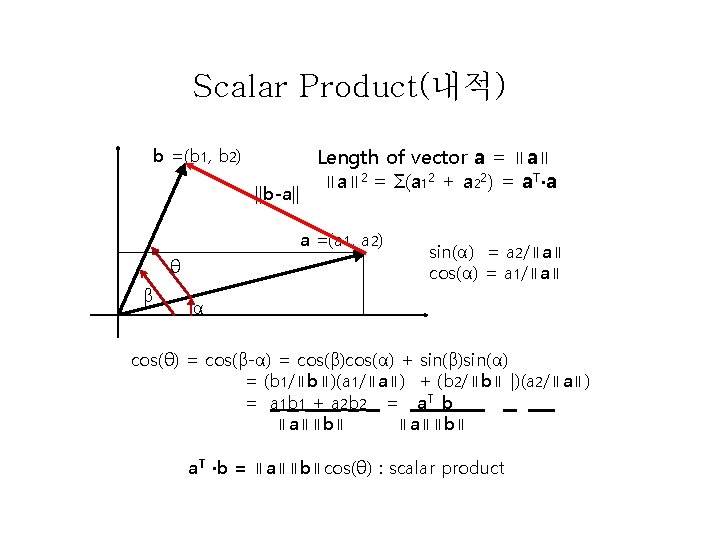
Scalar Product(내적) b =(b 1, b 2) ||b-a|| Length of vector a = ∥a∥ 2 = Σ(a 12 + a 22) = a. T∙a a =(a 1, a 2) θ β sin(α) = a 2/∥a∥ cos(α) = a 1/∥a∥ α cos(θ) = cos(β-α) = cos(β)cos(α) + sin(β)sin(α) = (b 1/∥b∥)(a 1/∥a∥) + (b 2/∥b∥ |)(a 2/∥a∥) = a 1 b 1 + a 2 b 2 = a T b ∥a∥∥b∥ a. T ∙b = ∥a∥∥b∥cos(θ) : scalar product

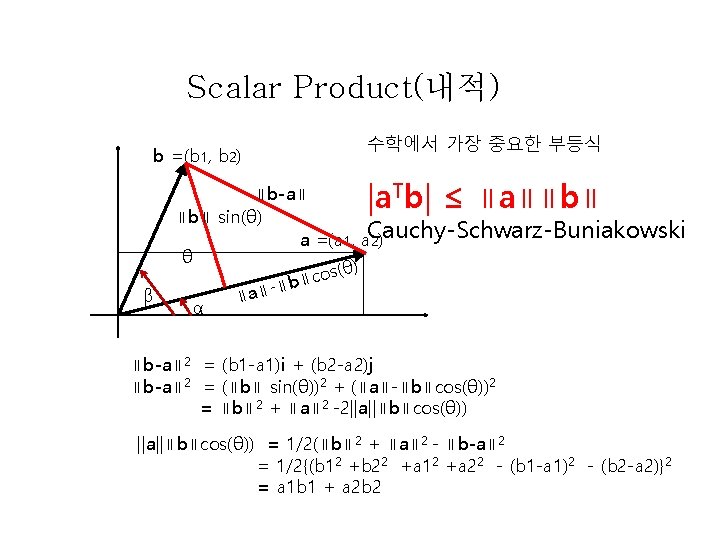
Angle Between Two Vectors cos(θ) = cos(β-α) = cos(β)cos(α) + sin(β)sin(α) = (b 1/∥b∥)(a 1/∥a∥) + (b 2/∥b∥ |)(a 2/∥a∥) = a 1 b 1 + a 2 b 2 = a T b ∥a∥∥b∥ a. T ∙b = ∥a∥∥b∥cos(θ) : scalar product 수학에서 가장 중요한 부등식 |a. Tb| ≤ ∥a∥∥b∥ Cauchy-Schwarz-Buniakowski

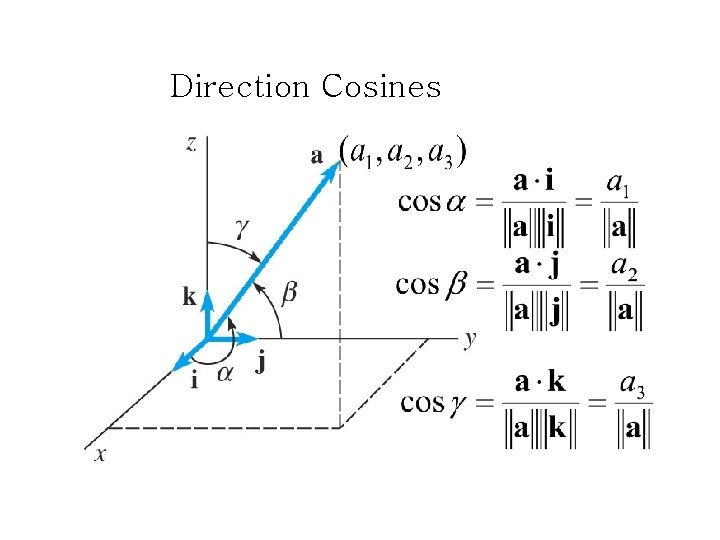
Direction Cosines

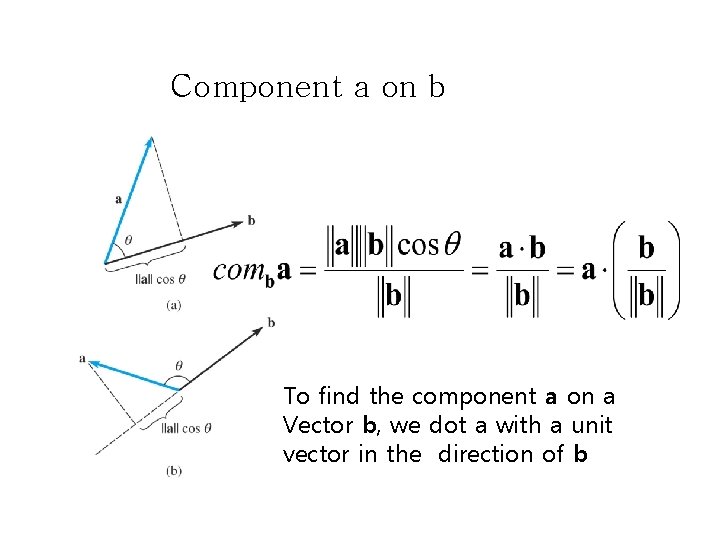
Component a on b To find the component a on a Vector b, we dot a with a unit vector in the direction of b

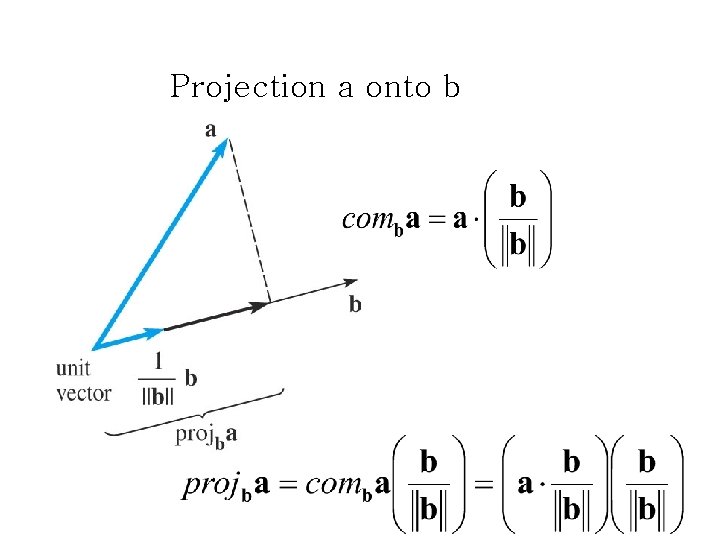
Projection a onto b

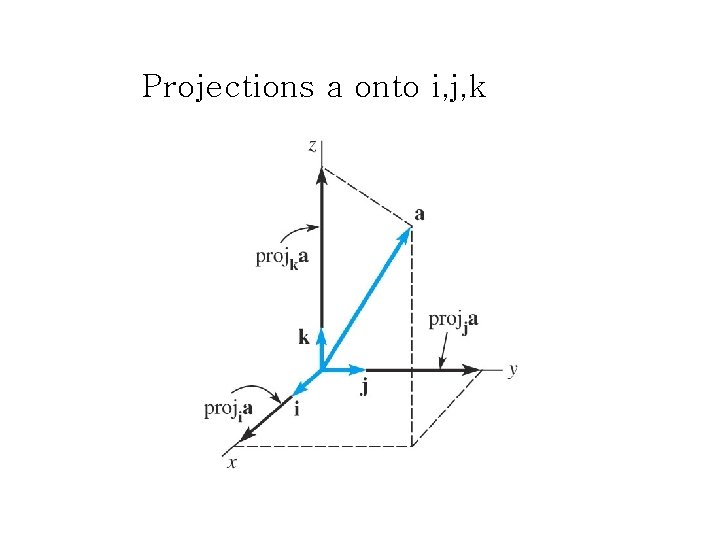
Projections a onto i, j, k

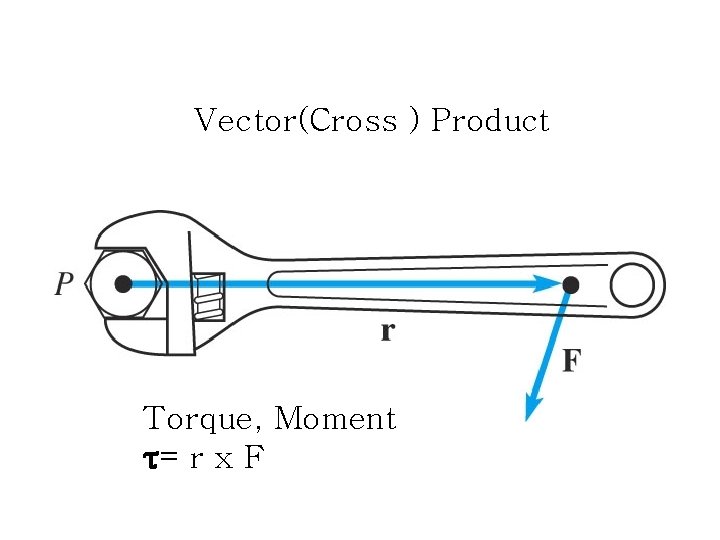
Vector(Cross ) Product Torque, Moment τ= r x F

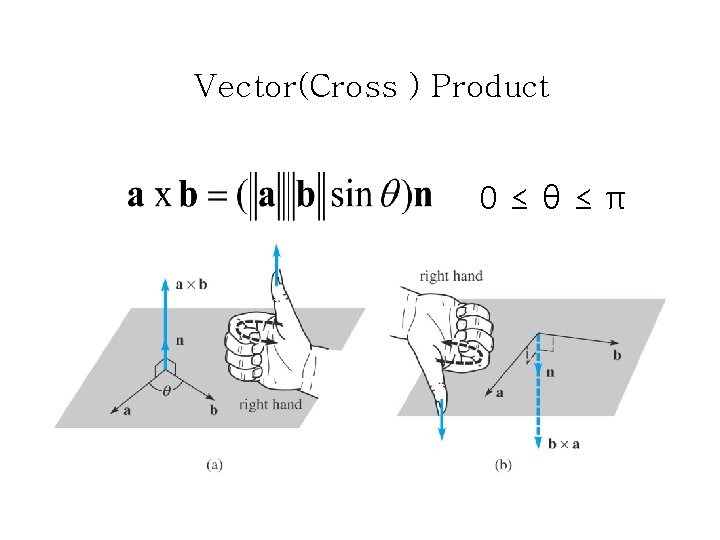
Vector(Cross ) Product 0≤θ≤π

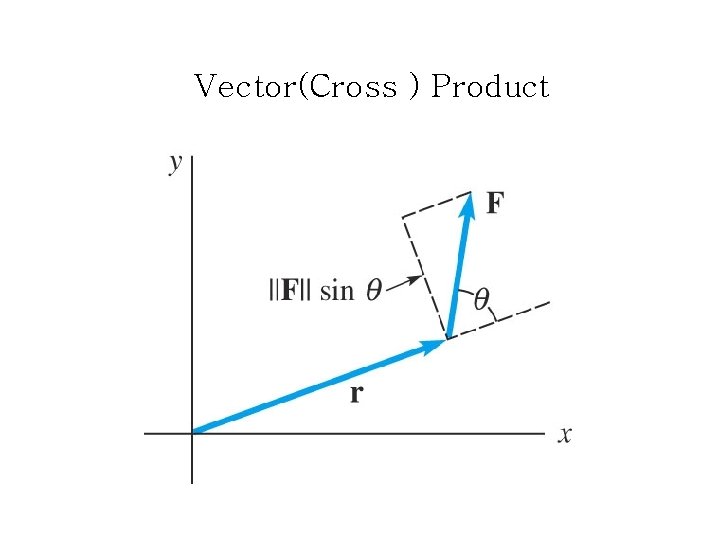
Vector(Cross ) Product

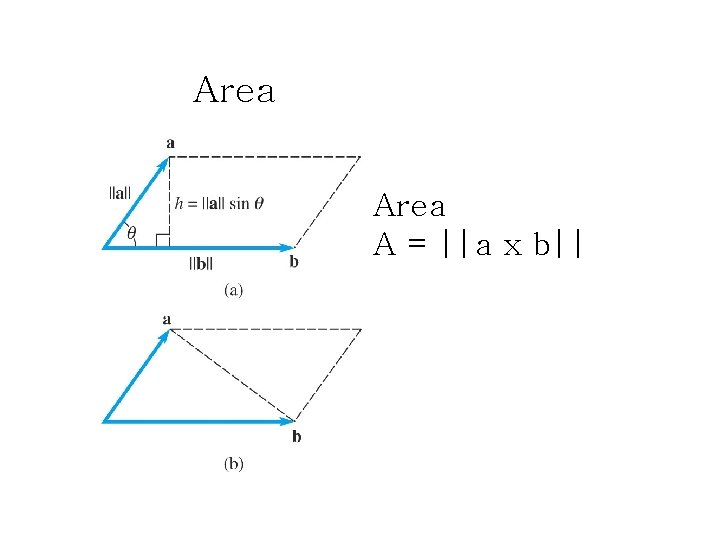
Area A = ||a x b||

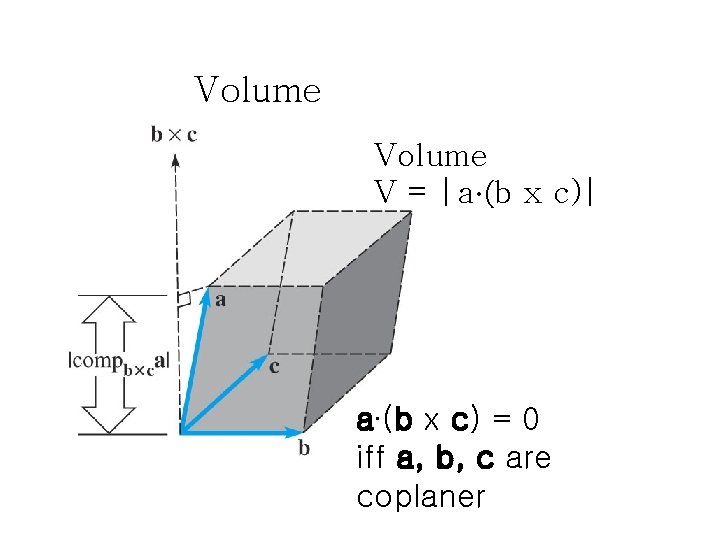
Volume V = |a∙(b x c)| a∙(b x c) = 0 iff a, b, c are coplaner

Vector(Cross ) Product Properties of the Cross product 1. a x b = 0 if a = 0 or b = 0 2. a x b = - b x a 3. a x (b + c) = (a x b) + (a x c) 4. (a + b) x c = (a x c) + (b x c) 5. a x (kb) = (ka) x b = k(a x b) 6. a x a = 0 7. a∙(a x b) = 0 8. b∙(a x b) = 0

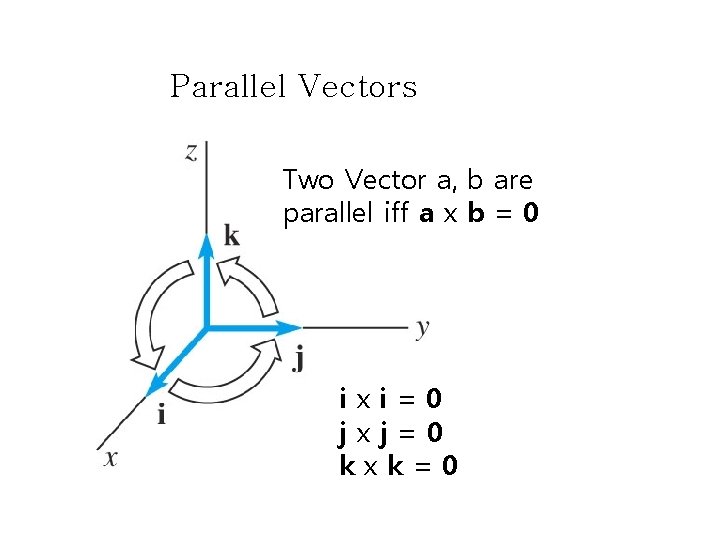
Parallel Vectors Two Vector a, b are parallel iff a x b = 0 ixi=0 jxj=0 kxk=0

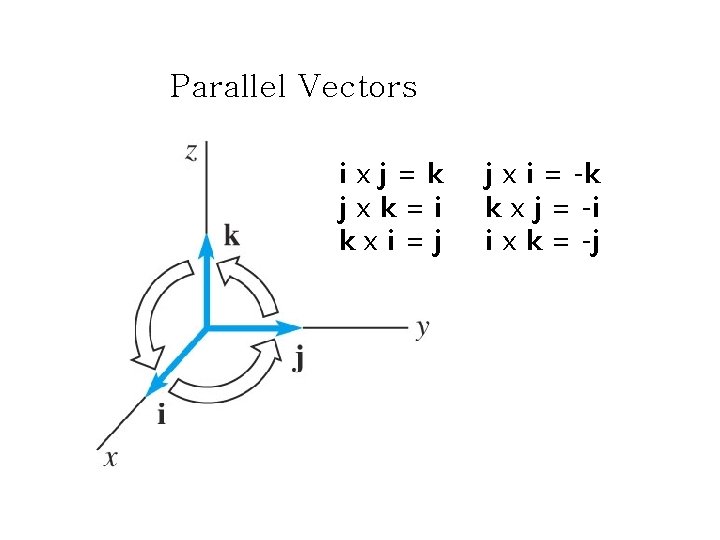
Parallel Vectors ixj=k jxk=i kxi=j j x i = -k k x j = -i i x k = -j

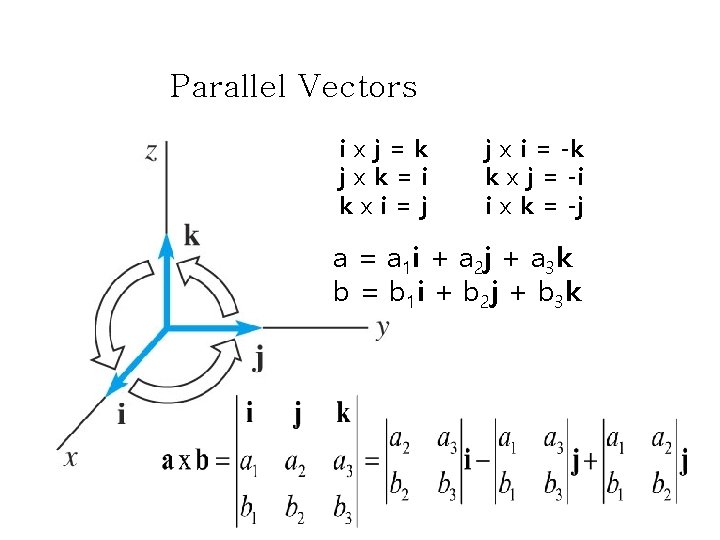
Parallel Vectors ixj=k jxk=i kxi=j j x i = -k k x j = -i i x k = -j a = a 1 i + a 2 j + a 3 k b = b 1 i + b 2 j + b 3 k