Scalar Vector Quantities SCALAR QUANTITIES Described by a

Scalar & Vector Quantities

SCALAR QUANTITIES • Described by a single number and unit of measurement. • Gives the magnitude (size) Examples Mass = 20 g Time = 20. 0 s Temperature = 20 o. C Speed = 20 m/s

VECTOR QUANTITIES • Arrows are used • Described by a single number and a unit of measurement (scalar) • Indicated direction. (head of arrow) Examples 30 m/s, East 30 m/s, N of E

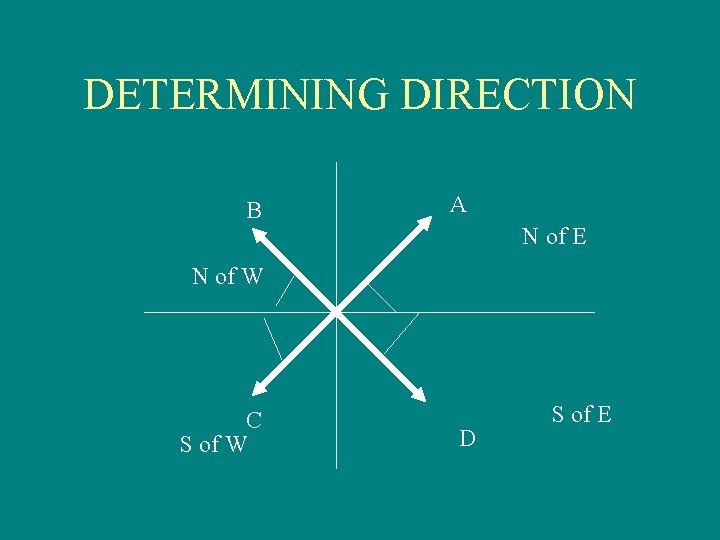
DETERMINING DIRECTION B A N of E N of W C S of W D S of E

ADDITION OF COLLINEAR VECTORS Resultant vector represent the total of two or more vectors drawn from the tail of the lst vector to the head of the last vector

VECTORS ACTING IN THE SAME DIRECTION Connect them head-to-tail and add Always indicate the direction of the resultant 10 km R = 20 km, 0 o E

VECTORS ACTING IN OPPOSITE DIRECTIONS Connect them tail to tail Subtract 20 km 10 km R = 10 km, 0 o, W

VECTORS ACTING AT A RIGHT ANGLE TO EACH OTHER • Connect head-to-tail • Draw resultant from the tail of the lst vector to the head of the second vector. • Determine resultant using pythagorean theorem • Determine angular direction by using the tan function

Pythagorean Theorem • C 2 = a 2 + b 2 • C = hypotenuse • A & B are sides

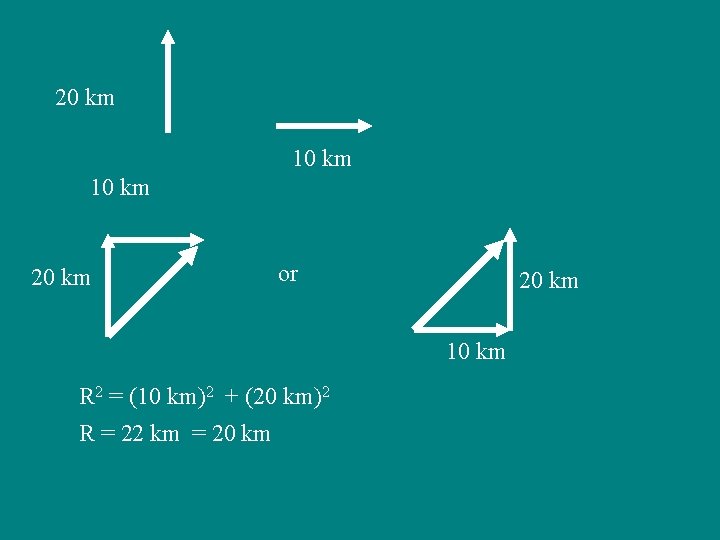
20 km 10 km 20 km or 20 km 10 km R 2 = (10 km)2 + (20 km)2 R = 22 km = 20 km

Determine angle makes with the X-axis. Use the correct number of significant figures. Tan = Y X = 20 km 10 km =2 = 63 o = 60 o

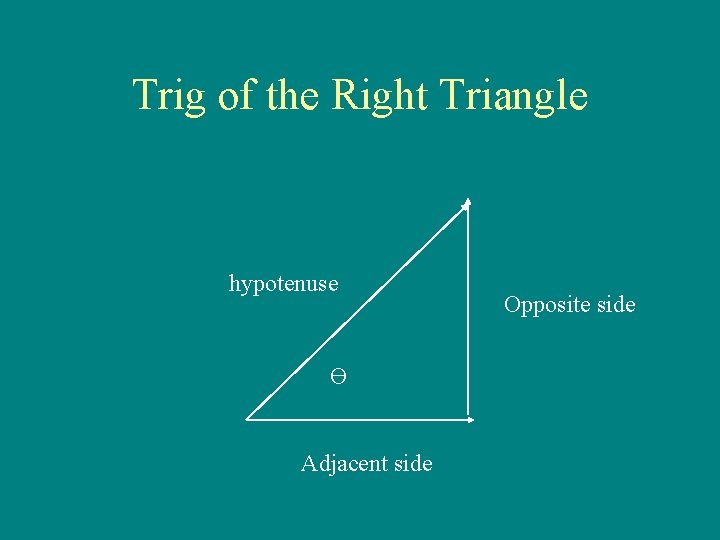
Trig of the Right Triangle hypotenuse Ө Adjacent side Opposite side

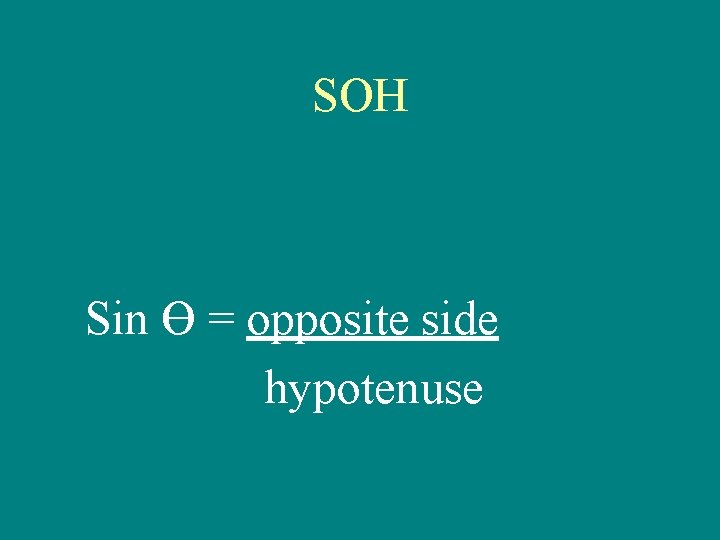
SOH Sin Ө = opposite side hypotenuse

CAH Cos Ө = adjacent side hypotenuse

TOA • Tan Ө = opposite side adjacent side

NON-COLLINEAR VECTORS A. Draw vectors on x-y axis B. Determine the X & Y components of C. each vector D. a. X-component = use Cos function E. b. Y-component = use Sin function F. c. Theta is 0 o if vector is located on X-axis G. d. Theta is 90 o if vector is located on Yaxis H. C. Indicate direction of vectors (+) and (-)

D. Add X-components E. Add Y-components F. Draw vectors representing the sum of the G. components head-to-tail. Signs (+) and (-) H. represents the direction of vectors. G. Draw Resultant H. Calculate R using Pythagorean Theorem I. Calculate theta II. J. Indicate direction relative to N, E, S or W

EXAMPLE Walk due west for 52 paces, then walk 30. 0 o North of West for 42 paces, and then walk due north for 25 paces. What are the magnitude and direction of the resultant, R

VECTOR DIAGRAM 42 52 25

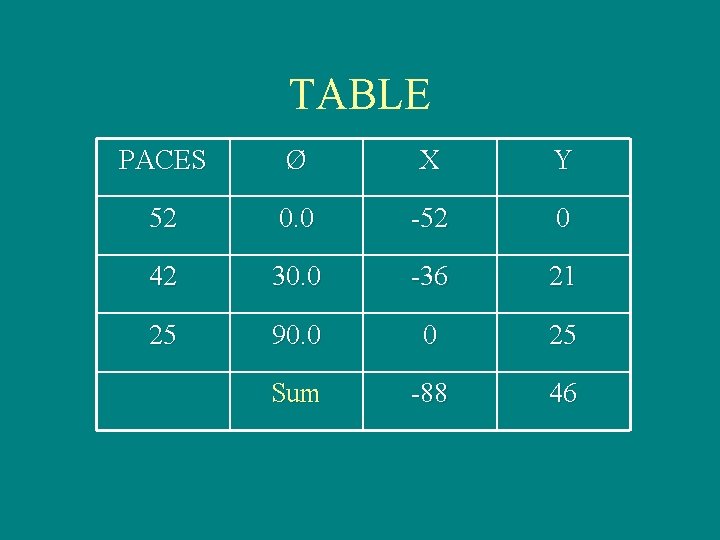
TABLE PACES Ø X Y 52 0. 0 -52 0 42 30. 0 -36 21 25 90. 0 0 25 Sum -88 46

DETERMINING DIRECTION OF RESULTANT DRAW TRIANGLE USING SUMS OF XAND Y-COMPONENTS 46 Paces R 88 Paces N of W

VALUE OF RESULTANT Use Pythagorean Theorem R 2 = (88 paces)2 + (46 paces)2 R = 99 paces

Angular Direction Use tan function tan = 46 paces 88 paces Ø = 28 o

FINAL ANSWER 99 Paces, 28 o, N of W

Units of Measurements MKS: meters (m), Kilogram (kg), second (s) kilometer (km), hour (h) CGS: centimeter (cm), gram (g), second (s) FPS: foot (ft. ), pound (lb. ), second (s) miles (mi. ), hour (h)