Geometric Intuition Randy Gaul Talk Outline Vectors Points


















































- Slides: 58

Geometric Intuition Randy Gaul

Talk Outline • • • Vectors, Points and Basis Matrices Rotation Matrices Dot product and how it’s useful Cross product and how it’s useful Extras

Prerequisites • • • Matrix multiplication How to apply dot/cross product Vector normalization Basic understanding of sin/cos Basic idea of what a plane is

Vectors • Formal definition – Input or output from a function of vector algebra • Informal definition – Scalar components representing a direction and magnitude (length) – Vectors have no “location”

Points and Vectors • A point P and Q is related to the vector V by: – P – Q = V • This implies that points can be translated by adding vectors

Points and Vectors (2) • Lets define an implied point O – O represents the origin • Any point P can be expressed with a vector V: – P = O + V • Vectors point to points, when relative to the origin!

Euclidean Basis • Standard Euclidean Basis (called E 3) – Geometrically the x, y and z axes

Euclidean Basis (2) • Given 3 scalars i, j and k, any point in E 3 can be represented

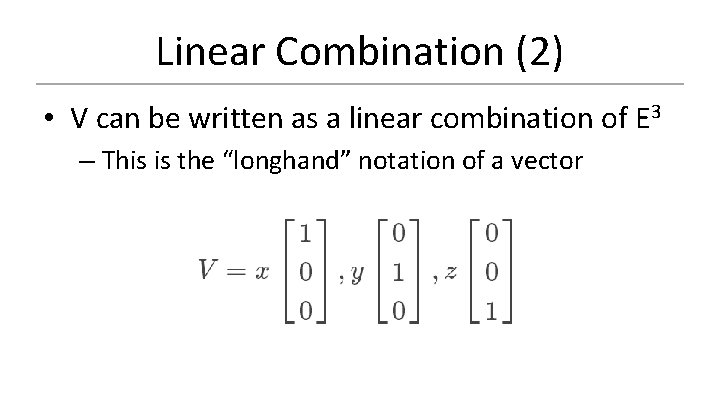
Linear Combination • Suppose we have a vector V – Consists of 3 scalar values – Below V written in “shorthand” notation

Linear Combination (2) • V can be written as a linear combination of E 3 – This is the “longhand” notation of a vector

Basis Matrices • E 3 is a basis matrix – Many matrices can represent a basis • Any vector can be represented in any basis Note: Different i, j and k values are used on left and right http: //en. wikipedia. org/wiki/Change_of_basis

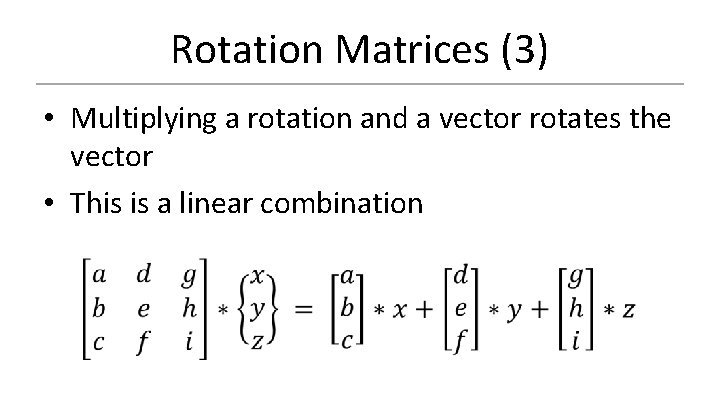
Rotation Matrices • A rotation matrix can rotate vectors – Constructed from 3 orthogonal unit vectors – Can be called an “orthonormal basis” • E 3 is a rotation matrix!

Rotation Matrices (2) • Rotation matrices consist of an x, y and z axis – Each axis is a vector X y z

Rotation Matrices (3) • Multiplying a rotation and a vector rotates the vector • This is a linear combination

Dot Product • Comes from law of cosines • Full derivation here • For two vectors u and v:

Shortest Angle Between 2 Vectors • Assume u and v are of unit length • Result in range of 0, 1 • No trig functions required

How Far in a Given Direction? • Given point P and vector V – How far along the V direction is P? x P V y

How Far in a Given Direction? (2)

Planes • Here’s the 3 D plane equation

Planes • Here’s the 3 D plane equation • WAIT A SECOND

Planes • Here’s the 3 D plane equation • WAIT A SECOND • THAT’S THE DOT PRODUCT

Planes (2) • a, b and c form a vector, called the normal • d is magnitude of the vector – Represents distance of plane from origin

Planes (3)

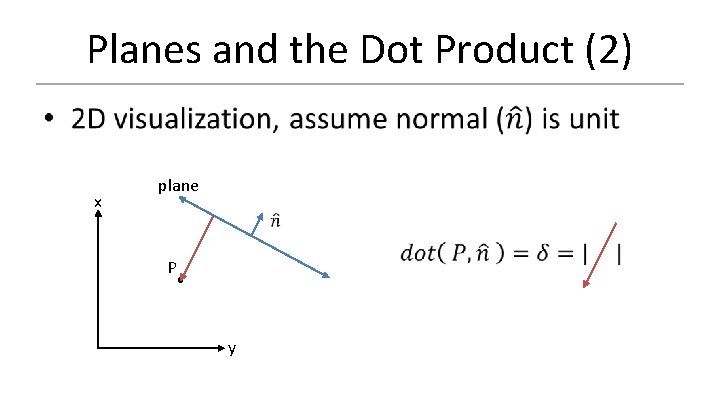
Planes and the Dot Product

Planes and the Dot Product (2) x plane P y

Signed Distance P to Plane

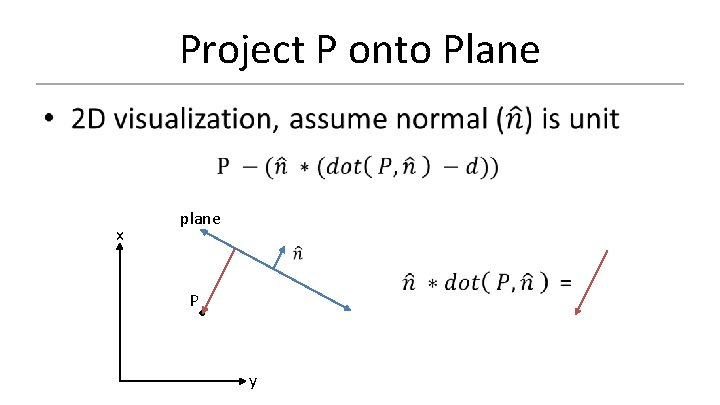
Project P onto Plane x plane P y

Rotation Matrices and Dot Product • Given matrices A and B • A * B is to dot the rows of A with columns of B • Lets assume A and B are rotation matrices http: //en. wikipedia. org/wiki/Matrix_multiplication

Rotation Matrices and Dot Product (2)

Rotation Matrices and Dot Product (3)

Rotation Matrices and Dot Product (4)

Rotation Matrices and Dot Product (5)

Point in Convex Hull • Test if point is inside of a hull – Compute plane equation of hull faces – Compute distance from plane with plane equation – If all distances are negative, point in hull – If any distance is positive, point outside hull • Works in any dimension • Can by used for basic frustum culling

Point in OBB • An OBB is a convex hull! – Hold your horses here… • Lets rotate point P into the frame of the OBB – OBB is defined with a rotation matrix, so invert it and multiply P by it – P is now in the basis of the OBB • The problem is now point in AABB

Point in Cylinder • Rotate cylinder axis to the z axis • Ignoring the z axis, cylinder is a circle on the xy plane • Test point in circle in 2 D – If miss, exit no intersection • Get points A and B. A is at top of cylinder, B at bottom • See if point’s z component is less than A’s and greater than B’s – Return intersection • No intersection

Bumper Car Damage? • Two bumper cars hit each other • One car takes damage • How much damage is dealt, and to whom?

Bumper Car Damage Answer • Take vector from one car to another, T • Damage dealt: – 1. 0 - Abs( Dot( velocity, T ) * collision. Damage )

http: //www. ra ndygaul. net/20 14/07/23/dista nce-point-toline-segment/


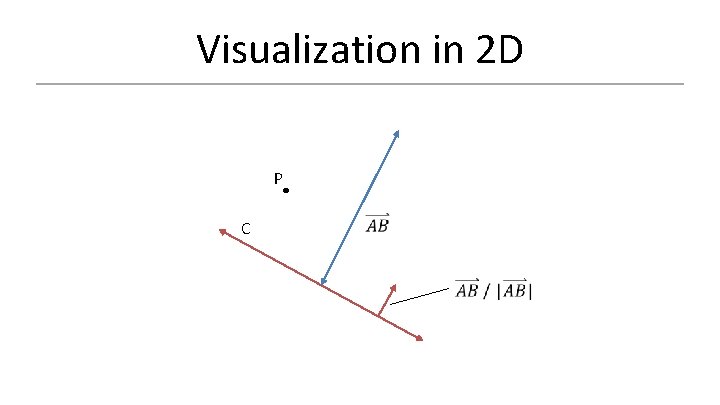
Visualization in 2 D P C

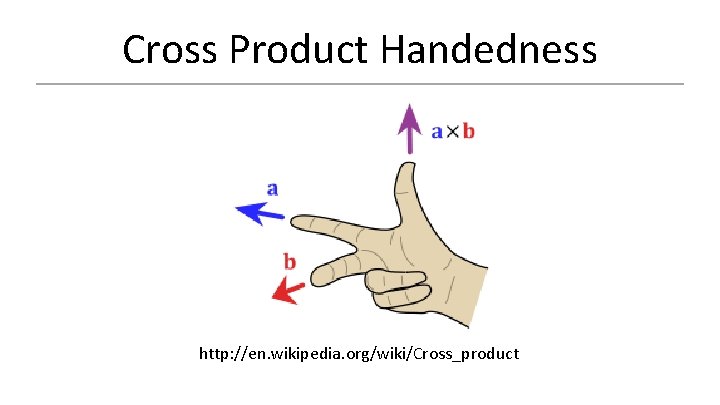
Cross Product • Operation between vectors • Produces a vector orthogonal to both input vectors

Cross Product Handedness http: //en. wikipedia. org/wiki/Cross_product

Cross Product Details http: //upload. wikimedia. org/wikipedia/commons/thumb/6/6 e/Cross_product. gif/2 20 px-Cross_product. gif

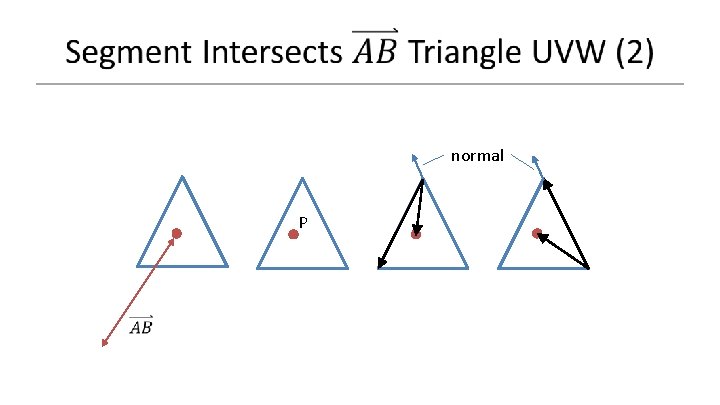
Plane Equation from 3 Points • • Given three points A, B and C Calculate normal with: Cross( C – A, B – A ) Normalize normal Compute offset d: dot( normal, A (or B or C) )

• Compute distance A to Plane: da • Compute distance B to Plane: db • If da * db < 0 – Intersection = A + (da / (da – db)) * (B – A) • Else – No intersection


normal P

Affine Transformations • Given matrix A, point x and vector b • An affine transformation is of the form: – Ax + b

Affine Transformations • Given 3 x 3 matrix A, point x and vector b • An affine transformation is of the form: – Ax + b • With a 4 x 4 matrix we can represent Ax + b in block formation:

Translation • Construct an affine transformation such that when multiplied with a point, translates the point by the vector b • I is the identity matrix, and means no rotation (or scaling) occurs

Translation (2) • The 1 is important, it means it is a point • If we had a zero here b wouldn’t affect x

Translation (3) • Proof that translation doesn’t affect vectors: – Translate from P to Q by T • • P – Q = T = (P + T) – (Q + T) = (P – Q) + (T – T) = P – Q

Rotation • Orthonormal basis into the top left of an affine transformation, without any translation vector:

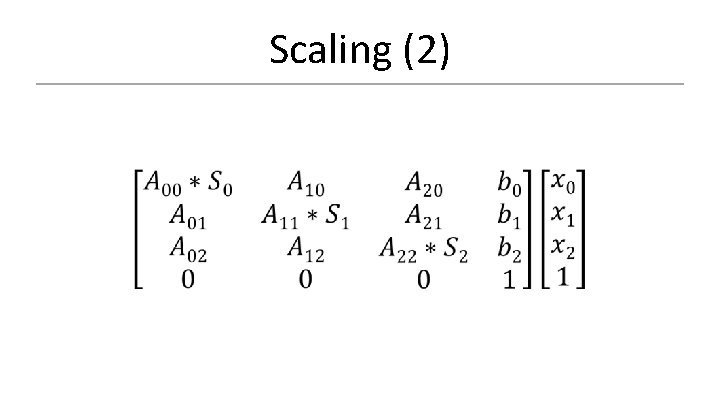
Scaling • • • Given scaling vector S Take the matrix A Scale A’s x axis’ x component by S 0 Scale A’s y axis’ y component by S 1 Scale A’s z axis’ z component by S 2

Scaling (2)

Camera - Look. At

Camera – Look. At (2) • Won’t work when player tries to look straight up or down – Parallel vectors crossed result in the zero vector • Possible solutions: – Snap player’s view away from up/down – Use an if statement and cross with a different up vector – More solutions exist!

Barycentric Coordinates • Slightly out of scope of this presentation • See Erin Catto’s GDC 2010 lecture • Idea: – Like a linear combination, try affine combinations of points • Useful for: – Voronoi region identification, collision detection, certain graphics or shader effects
 Orsolya gaul
Orsolya gaul Aphrodite of knidos period
Aphrodite of knidos period Scraper
Scraper What products came from the farms of italy gaul and spain
What products came from the farms of italy gaul and spain Geometric representation of vectors worksheet answers
Geometric representation of vectors worksheet answers Geometric representation of vectors
Geometric representation of vectors Geometric description of vectors
Geometric description of vectors Talk, read, talk, write resources
Talk, read, talk, write resources Amateurs talk tactics professionals talk logistics
Amateurs talk tactics professionals talk logistics The words use are not
The words use are not 2018 geometry bootcamp answers
2018 geometry bootcamp answers Points of parity and points of difference
Points of parity and points of difference Points of parity and points of difference
Points of parity and points of difference Delivery cues on a speaking outline
Delivery cues on a speaking outline Unorganized points and outline structure
Unorganized points and outline structure Green's theorem intuition
Green's theorem intuition Rationalism vs romanticism
Rationalism vs romanticism Lagrange method
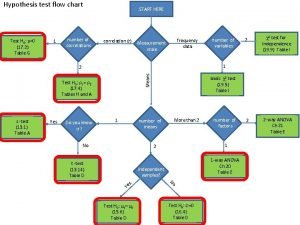
Lagrange method Flow diagram of hypothesis testing
Flow diagram of hypothesis testing Responding to economic pressures in ob
Responding to economic pressures in ob Gisle henden
Gisle henden Intuition examples
Intuition examples Feeling and intuition over reason
Feeling and intuition over reason Intuition vs sensing
Intuition vs sensing Understanding your intuition
Understanding your intuition Intuition pumps examples
Intuition pumps examples My intuition is telling me therell be better days
My intuition is telling me therell be better days Test intuition
Test intuition Values feeling and intuition over reason
Values feeling and intuition over reason Dot product intuition
Dot product intuition Support vector machine intuition
Support vector machine intuition Values feeling and intuition over reason
Values feeling and intuition over reason Favoring intuition over reason
Favoring intuition over reason Intuition definition
Intuition definition Skewed distributions
Skewed distributions A mental grouping of similar objects
A mental grouping of similar objects Intuition feeling thinking sensing
Intuition feeling thinking sensing Quote sandwich examples
Quote sandwich examples Randy huffman west virginia
Randy huffman west virginia Randy morin
Randy morin Randy schoephoerster
Randy schoephoerster Zachary hensley
Zachary hensley Randy marchany
Randy marchany Randy canis
Randy canis Dr jess demaria
Dr jess demaria Randy kuiper
Randy kuiper Randy pausch carnegie mellon
Randy pausch carnegie mellon Randy adderson personality
Randy adderson personality Peas porridge hot meaning
Peas porridge hot meaning Randy francis
Randy francis Mateo 13 44 dibujo
Mateo 13 44 dibujo Dr randal betz
Dr randal betz Fasstmath
Fasstmath Randy canis
Randy canis Randy hanzlick
Randy hanzlick Randy schoephoerster
Randy schoephoerster William shatner
William shatner Randy harp
Randy harp Randy ruggles
Randy ruggles