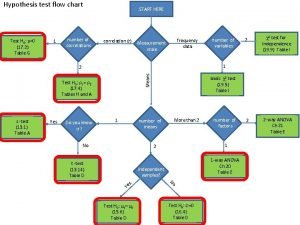
Hypothesis test flow chart Test H 0 r0















- Slides: 28

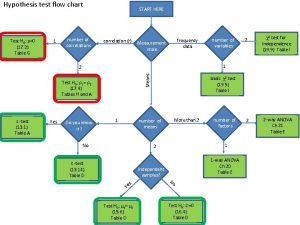
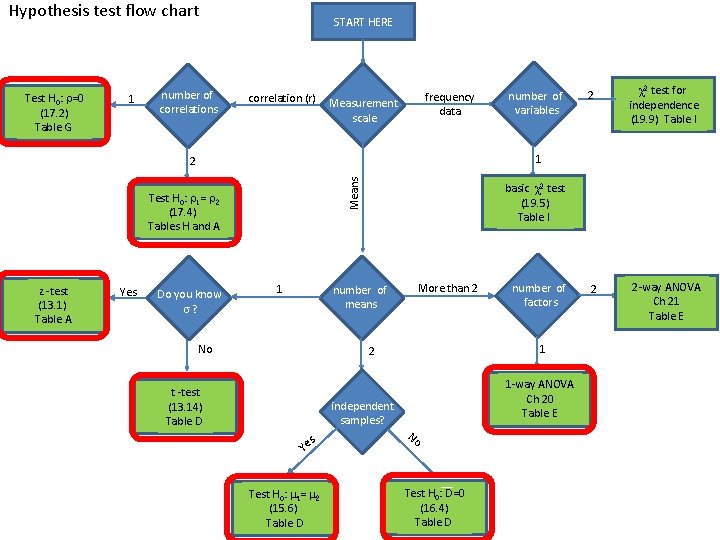
Hypothesis test flow chart Test H 0: r=0 (17. 2) Table G 1 number of correlations START HERE correlation (r) frequency data Measurement scale Means Test H 0: r 1= r 2 (17. 4) Tables H and A Yes 2 χ2 test for independence (19. 9) Table I 2 2 -way ANOVA Ch 21 Table E 1 2 z -test (13. 1) Table A number of variables Do you know s? 1 basic χ2 test (19. 5) Table I More than 2 number of means No 1 2 t -test (13. 14) Table D independent samples? s Ye Test H 0: m 1= m 2 (15. 6) Table D number of factors 1 -way ANOVA Ch 20 Table E No Test H 0: D=0 (16. 4) Table D

Chapter 18: Testing for difference among three or more groups: One way Analysis of Variance (ANOVA) A B C 84 85 62 78 62 79 93 62 83 76 74 79 92 71 80 68 81 74 79 69 84 76 87 67 81 68 67 87 61 75 Suppose you wanted to compare the results of three tests (A, B and C) to see if there was any differences difficulty. To test this, you randomly sample these ten scores from each of the three populations of test scores. How would you test to see if there was any difference across the mean scores for these three tests? The first thing is obvious – calculate the mean for each of the three samples of 10 scores. Means 81 72 75 But then what? You could run three two-sample t-tests on each of the pairs (A vs. B, A vs. C and B vs. C).

A B C 84 85 62 78 62 79 93 62 83 76 74 79 92 71 80 68 81 74 79 69 84 76 87 67 81 68 67 87 61 75 Means 81 72 75 You could run an two-sample t-test on each of the pairs (A vs. B, A vs. C and B vs. C). There are two problems with this: 1) The three tests wouldn’t be truly independent of each other, since they contain common values, and 2) We run into the problem of making multiple comparisons: If we use an a value of. 05, the probability of obtaining at least one significant comparison by chance is 1 -(1 -. 05)3, or about. 14 So how do we test the null hypothesis: H 0: m. A = m. B = m. C ?

So how do we test the null hypothesis: H 0: m. A = m. B = m. C ? In the 1920’s Sir Ronald Fisher developed a method called ‘Analysis of Variance’ or ANOVA to test hypotheses like this. A B C 84 85 62 78 62 79 93 62 83 76 74 79 92 71 80 68 81 74 79 69 84 76 87 67 81 68 67 87 61 75 Means 81 72 75 The trick is to look at the amount of variability between the means. So far in this class, we’ve usually talked about variability in terms of standard deviations. ANOVA’s focus on variances instead, which (of course) is the square of the standard deviation. The intuition is the same. The variance of these three mean scores (81, 72 and 75) is 22. 5 Intuitively, you can see that if the variance of the means scores is ‘large’, then we should reject H 0. But what do we compare this number 22. 5 to?

So how do we test the null hypothesis: H 0: m. A = m. B = m. C ? The variance of these three mean scores (81, 72 and 75) is 22. 5 How ‘large’ is 22. 5? A B C 84 85 62 78 62 79 93 62 83 76 74 79 92 71 80 68 81 74 79 69 84 76 87 67 81 68 67 87 61 75 Means 81 72 75 Suppose we knew the standard deviation of the population of scores (s). If the null hypothesis is true, then all scores across all three columns are drawn from a population with standard deviation s. It follows that the mean of n scores should be drawn from a population with standard deviation: With a little algebra: This means multiplying the variance of the means by n gives us an estimate of the variance of the population.

The variance of these three mean scores (81, 72 and 75) is 22. 5 Multiplying the variance of the means by n gives us an estimate of the variance of the population. A B C 84 85 62 78 62 79 93 62 83 76 74 79 92 71 80 68 81 74 79 69 84 76 87 67 81 68 67 87 61 75 Means 81 72 94 We typically don’t know what s 2 is. But like we do for t-tests, we can use the variance within our samples to estimate it. The variance of the 10 numbers in each column (61, 94, and 55) should each provide an estimate of s 2. We can combine these three estimates of s 2 by taking their average, which is 70. n x Variance of means 75 Variances 61 For our example, 225 Mean of variances 55 70

If H 0: m. A = m. B = m. C is true, we now have two separate estimates of the variance of the population (s 2). A B C 84 85 62 78 62 79 93 62 83 76 74 79 92 71 80 68 81 74 79 69 84 76 87 67 81 68 67 87 61 75 Means 81 72 94 If H 0 is true, then these two numbers should be, on average, the same, since they’re both estimates of the same thing (s 2). For our example, these two numbers (225 and 70) seem quite different. Remember our intuition that a large variance of the means should be evidence against H 0. Now we have something to compare it to. 225 seems large compared to 70. n x Variance of means 75 Variances 61 One is n times the variance of the means of each column. The other is the mean of the variances of each column. 225 Mean of variances 55 70

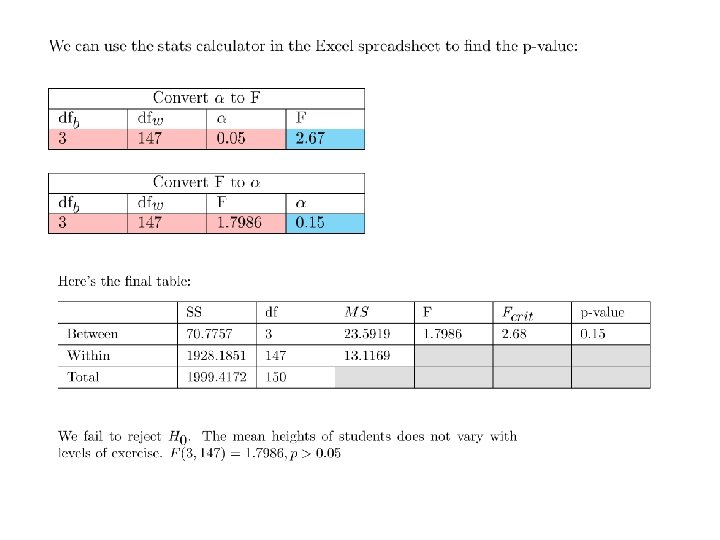
When conducting an ANOVA, we compute the ratio of these two estimates of s 2. This ratio is called the ‘F statistic’. For our example, 225/70 = 3. 23. A B C 84 85 62 78 62 79 93 62 83 76 74 79 92 71 80 68 81 74 79 69 84 76 87 67 81 68 67 87 61 75 Means 81 72 94 We determine how large F should be for rejecting H 0 by looking up Fcrit in Table E. F distributions depend on two separate degrees of freedom – one for the numerator and one for the denominator. df for the numerator is k-1, where k is the number of columns or ‘treatments’. For our example, df is 3 -1 =2. df for the denominator is N-k, where N is the total number of scores. In our case, df is 30 -3 = 27. n x Variance of means 75 Variances 61 If H 0 is true, then the value of F should be around 1. If H 0 is not true, then F should be significantly greater than 1. 225 Mean of variances 55 70 Ratio (F) Fcrit for a =. 05 and df’s of 2 and 27 is 3. 35. 3. 23 Since Fobs = 3. 23 is less than Fcrit, we fail to reject H 0. We cannot conclude that the exam scores come from populations with different means.

Fcrit for a =. 05 and df’s of 2 and 27 is 3. 35. Since Fobs = 3. 23 is less than Fcrit, we fail to reject H 0. We cannot conclude that the exam scores come from populations with different means. Instead of finding Fcrit in Table E, we could have calculated the p-value using our Fcalculator. Reporting p-values is standard. Our p-value for F=3. 23 with 2 and 27 degrees of freedom is p=. 0552 Since our p-value is greater then. 05, we fail to reject H 0

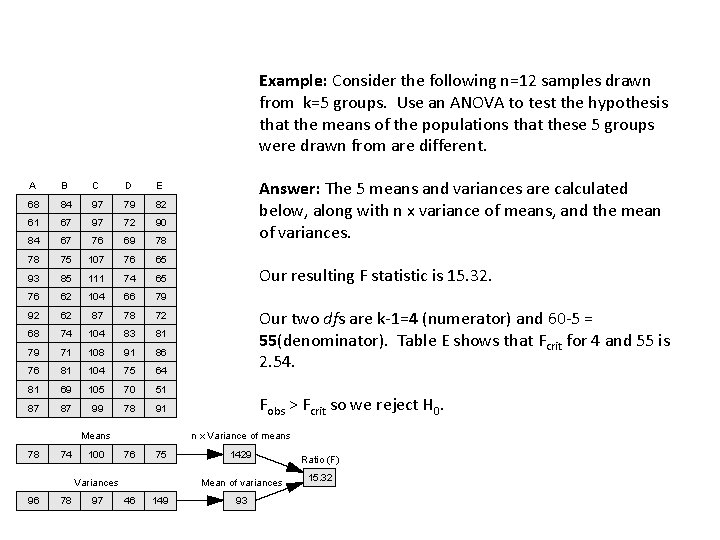
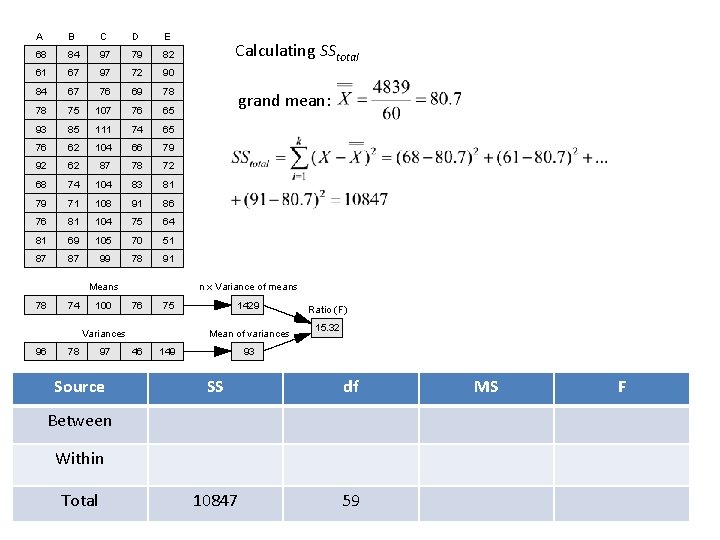
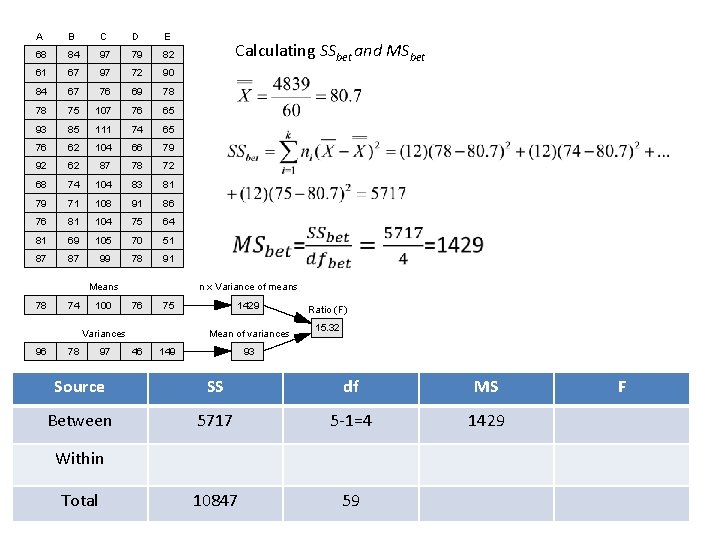
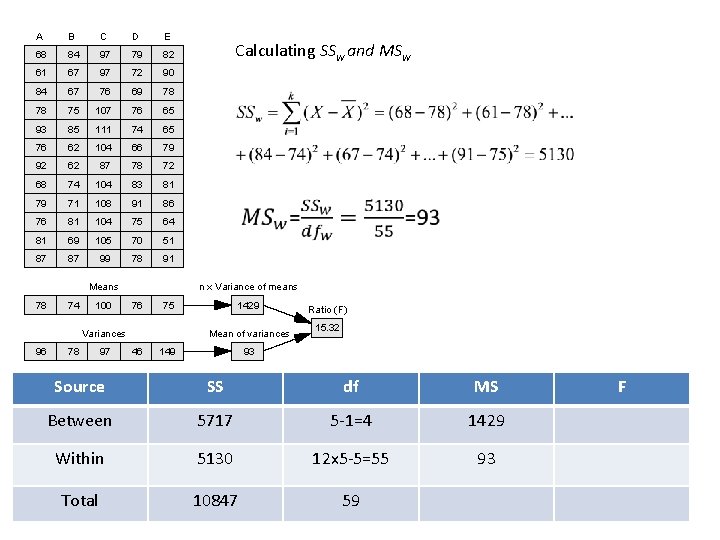
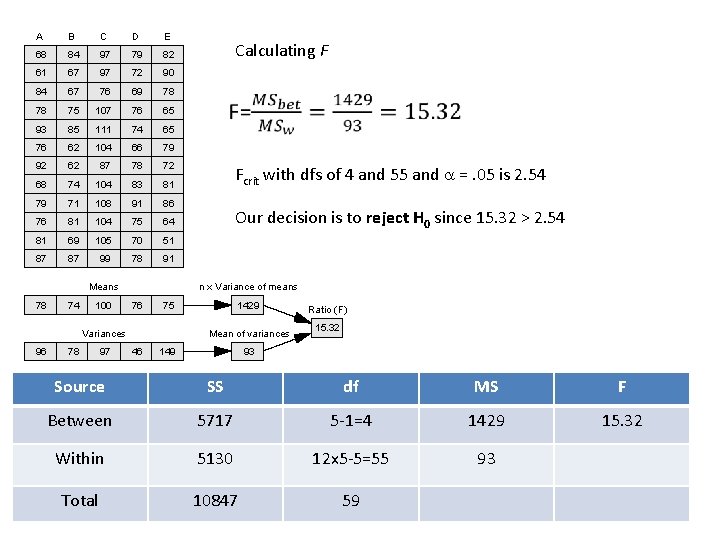
Example: Consider the following n=12 samples drawn from k=5 groups. Use an ANOVA to test the hypothesis that the means of the populations that these 5 groups were drawn from are different. A B C D E 68 84 97 79 82 61 67 97 72 90 84 67 76 69 78 78 75 107 76 65 93 85 111 74 65 76 62 104 66 79 92 62 87 78 72 68 74 104 83 81 79 71 108 91 86 76 81 104 75 64 81 69 105 70 51 87 87 99 78 91 Means 78 74 100 78 97 Our resulting F statistic is 15. 32. Our two dfs are k-1=4 (numerator) and 60 -5 = 55(denominator). Table E shows that Fcrit for 4 and 55 is 2. 54. Fobs > Fcrit so we reject H 0. n x Variance of means 76 75 Variances 96 Answer: The 5 means and variances are calculated below, along with n x variance of means, and the mean of variances. 1429 Mean of variances 46 149 93 Ratio (F) 15. 32

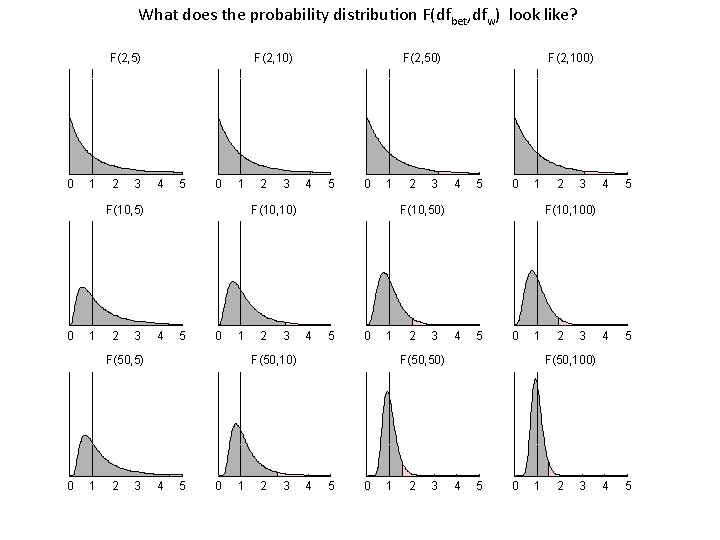
What does the probability distribution F(dfbet, dfw) look like? F(2, 5) 0 1 2 3 F(2, 10) 4 5 0 1 F(10, 5) 0 1 2 3 3 4 5 0 1 F(10, 10) 4 5 0 1 F(50, 5) 0 2 F(2, 50) 2 3 5 0 1 2 3 3 4 5 0 1 F(10, 50) 4 5 0 1 F(50, 10) 4 2 F(2, 100) 2 3 5 0 1 2 3 3 4 5 4 5 F(10, 100) 4 5 0 1 F(50, 50) 4 2 2 3 F(50, 100) 4 5 0 1 2 3

For a typical ANOVA, the number of samples in each group may be different, but the intuition is the same - compute F which is the ratio of the variance of the means over the mean of the variances. Formally, the variance is divided up the following way: Given a table of k groups, each containing ni scores (i= 1, 2, …, k), we can represent the deviation of a given score, X from the mean of all scores, called the grand mean as: Deviation of X from the grand mean Deviation of X from the mean of the group Deviation of the mean of the group from the grand mean

The total sums of squares can be partitioned into two numbers: Total sum of squares: SStotal Within-groups sum of squares: SSw Between-groups sum of squares: SSbet is a measure of the variability between groups. It is used as the numerator in our F-tests The variance between groups, called ‘mean squared error’, or MSbet, is calculated by dividing SSbet by its degrees of freedom dfbet = k-1 MSbet=SSbet/dfbet and is another estimate of s 2 if H 0 is true. This is essentially n times the variance of the means. . If H 0 is not true, then s 2 bet is an estimate of s 2 plus any ‘treatment effect’ that would add to a difference between the means.

The total sums of squares can be partitioned into two numbers: Total sum of squares: SStotal Within-groups sum of squares: SSw Between-groups sum of squares: SSbet SSw is a measure of the variability within each group. It is used as the denominator in all F-tests. The variance within each group, MSw is calculated by dividing SSw by its degrees of freedom dfw = ntotal – k MSw=SSw/dfw This is an estimate of s 2 This is essentially the mean of the variances within each group. (It is exactly the mean of variances if our sample sizes are all the same. )

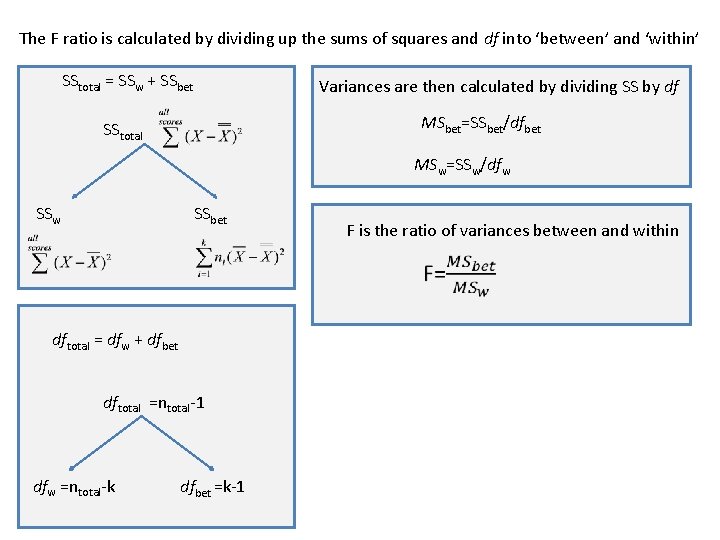
The F ratio is calculated by dividing up the sums of squares and df into ‘between’ and ‘within’ SStotal = SSw + SSbet Variances are then calculated by dividing SS by df MSbet=SSbet/dfbet SStotal MSw=SSw/dfw SSbet F is the ratio of variances between and within dftotal = dfw + dfbet dftotal =ntotal-1 dfw =ntotal-k dfbet =k-1

Finally, the F ratio is the ratio of MSbet and MSw We can write all these calculated values in a summary table like this: Source SS df MS Between k-1 MSbet=SSbet/dfbet Within ntotal-k MSw=SSw/dfw Total ntotal-1 F (k is the number of groups)

A B C D E 68 84 97 79 82 61 67 97 72 90 84 67 76 69 78 78 75 107 76 65 93 85 111 74 65 76 62 104 66 79 92 62 87 78 72 68 74 104 83 81 79 71 108 91 86 76 81 104 75 64 81 69 105 70 51 87 87 99 78 91 Means 78 74 100 78 97 Source grand mean: n x Variance of means 76 75 Variances 96 Calculating SStotal 1429 Mean of variances 46 149 Ratio (F) 15. 32 93 SS df 10847 59 Between Within Total MS F

A B C D E 68 84 97 79 82 61 67 97 72 90 84 67 76 69 78 78 75 107 76 65 93 85 111 74 65 76 62 104 66 79 92 62 87 78 72 68 74 104 83 81 79 71 108 91 86 76 81 104 75 64 81 69 105 70 51 87 87 99 78 91 Means 78 74 100 78 97 n x Variance of means 76 75 Variances 96 Calculating SSbet and MSbet 1429 Mean of variances 46 149 Ratio (F) 15. 32 93 Source SS df MS Between 5717 5 -1=4 1429 10847 59 Within Total F

A B C D E 68 84 97 79 82 61 67 97 72 90 84 67 76 69 78 78 75 107 76 65 93 85 111 74 65 76 62 104 66 79 92 62 87 78 72 68 74 104 83 81 79 71 108 91 86 76 81 104 75 64 81 69 105 70 51 87 87 99 78 91 Means 78 74 100 78 97 n x Variance of means 76 75 Variances 96 Calculating SSw and MSw 1429 Mean of variances 46 149 Ratio (F) 15. 32 93 Source SS df MS Between 5717 5 -1=4 1429 Within 5130 12 x 5 -5=55 93 Total 10847 59 F

A B C D E 68 84 97 79 82 61 67 97 72 90 84 67 76 69 78 78 75 107 76 65 93 85 111 74 65 76 62 104 66 79 92 62 87 78 72 68 74 104 83 81 79 71 108 91 86 76 81 104 75 64 81 69 105 70 51 87 87 99 78 91 Means 78 74 100 78 97 Fcrit with dfs of 4 and 55 and a =. 05 is 2. 54 Our decision is to reject H 0 since 15. 32 > 2. 54 n x Variance of means 76 75 Variances 96 Calculating F 1429 Mean of variances 46 149 Ratio (F) 15. 32 93 Source SS df MS F Between 5717 5 -1=4 1429 15. 32 Within 5130 12 x 5 -5=55 93 Total 10847 59








 Hypothesis flow chart
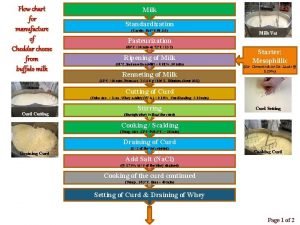
Hypothesis flow chart Cheese process flow chart
Cheese process flow chart Example of alternative hypothesis
Example of alternative hypothesis Alternative hypothesis
Alternative hypothesis Examples of null hypothesis
Examples of null hypothesis Protoplanet hypothesis weakness
Protoplanet hypothesis weakness Flsa exemption test flow chart
Flsa exemption test flow chart Rafael perera
Rafael perera Statistical test flow chart
Statistical test flow chart Statistical test flow chart
Statistical test flow chart Pressure flow hypothesis
Pressure flow hypothesis Phloem
Phloem Magic box oxygen therapy
Magic box oxygen therapy Venturi mask flow rate
Venturi mask flow rate Non rebreather mask definition
Non rebreather mask definition Reynolds number
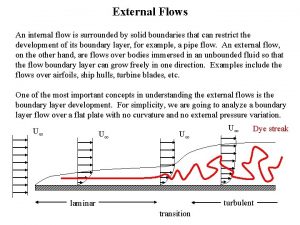
Reynolds number Internal and external flow
Internal and external flow Energy naturally flows from warmer matter to cooler matter
Energy naturally flows from warmer matter to cooler matter Flow of energy vs flow of matter
Flow of energy vs flow of matter Structure chart in software engineering
Structure chart in software engineering Transform flow and transaction flow
Transform flow and transaction flow Rotational and irrotational flow examples
Rotational and irrotational flow examples External flow vs internal flow
External flow vs internal flow Data flow vs control flow
Data flow vs control flow Control flow and data flow computers
Control flow and data flow computers Transaction flow testing
Transaction flow testing T value
T value Two tailed test p value
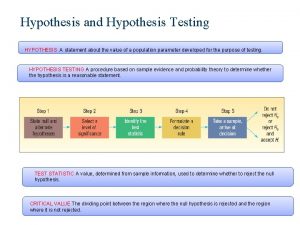
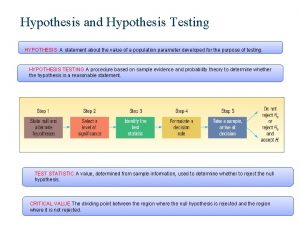
Two tailed test p value Hypothesis testing definition
Hypothesis testing definition