Introduction to MATLAB and Simulink CFSEAS Workshop George

Introduction to MATLAB and Simulink CFSEAS Workshop George Washington University Prepared by: Farhad

Outline � Section I (Jan 30 th, 2016) ◦ Background ◦ Basic Syntax and Commands ◦ Linear Algebra ◦ Loops � Section II (Feb 6 st, 2016) ◦ Graphing & Plots ◦ Scripts and Functions � Section III (Feb 20 th, 2016) ◦ Linear & System of Equations Solving ◦ ODE Solving � Section IV (Mar 5 th, 2016) ◦ Simulink

Section I January 30 th, 2015 ◦ ◦ Background Basic Syntax and Commands Linear Algebra Loops
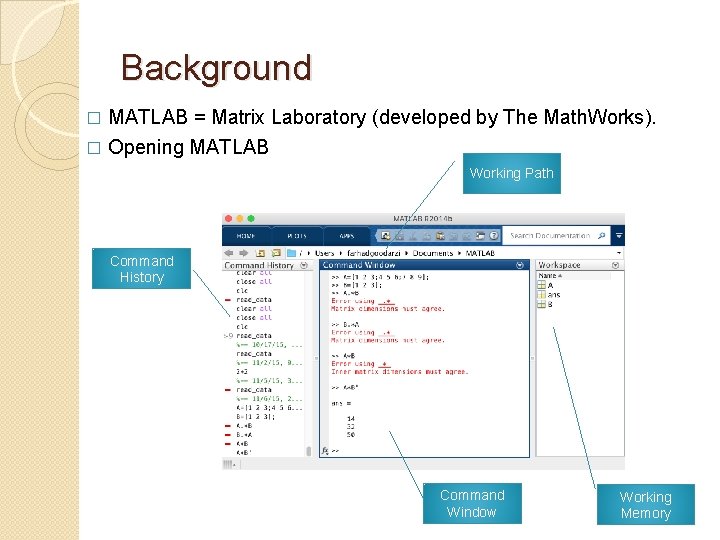
Background MATLAB = Matrix Laboratory (developed by The Math. Works). � Opening MATLAB � Working Path Command History Command Window Working Memory

Variables Have not to be previously declared � Variable names can contain up to 63 characters � � Variable names must start with a letter followed by letters, digits, and underscores( Valid: x 1 = 5, Invalid: 1 x = 5) � Variable names are case sensitive (a 1 does NOT equal A 1) Operators � EX: Using command window � >> x = 5; % this is used as a comment � >> y = 3; � >> z = x + y z=8 Semicolon (; ) : Suppresses output � Percentage (%) : Commenting. Only good for that line �

MATLAB Special Variables ans Default variable name for results pi Value of pi number (3. 14) eps Smallest incremental number inf Infinity Na. N Not a number e. g. 0/0 realmin The smallest usable positive real number realmax The largest usable positive real number i, j Imaginary unit

MATLAB Assignment & Operators Assignment = a = b (assign b to a) Addition + a+b Subtraction - a-b Multiplication * or. * a*b or a. *b Division / or. / a/b or a. /b Power ^ . ^ a^b or a. ^b

MATLAB Matrices � MATLAB treats all variables as matrices. For our purposes a matrix can be thought of as an array, in fact, that is how it is stored. � Vectors are special forms of matrices and contain only one row OR one column. � Scalars are matrices with only one row AND one column

MATLAB Matrices � A matrix with only one row is called a row vector. A row vector can be created in MATLAB as follows (note the commas): » rowvec = [12 , 14 , 63] rowvec = 12 14 63 � A matrix with only one column is called a column vector. A column vector can be created in MATLAB as follows (note the semicolons): » colvec = [13 ; 45; -2] colvec = 13 45 -2

MATLAB Matrices � A matrix can be created in MATLAB as follows (note the commas AND semicolons): » matrix = [1 , 2 , 3 ; 4 , 5 , 6 ; 7 , 8 , 9] matrix = 123 456 789

Index � MATLAB index starts with 1, NOT 0! � Vector Index: ◦ a = [22 17 7 4 42] �a(1) = 22 �a(3) = 7 � Matrix Index: ◦ a = [7 12 42; 5 1 23; 4 9 10]; �a(1, 3) = 42 �a(3, 2) = 9

Some matrix functions in MATLAB X = ones(r, c) Creates matrix full with ones X = zeros(r, c) Creates matrix full with zeros A = diag(x) Creates squared matrix with vector x in diagonal [r, c] = size(A) Return dimensions of matrix A X = A’ Transposed matrix X = inv(A) Inverse matrix squared matrix X = pinv(A) Pseudo inverse d = det(A) Determinant [X, D] = eig(A) Eigenvalues and eigenvectors [U, D, V] = svd(A) singular value decomposition

Dot Operator For scalar operations, nothing new is needed. Example: a = 5; b = 3; ==> c = a*b %c = 15 � For element operations, a dot must be used before the operator. � Note: Dot operator not the same as dot product! � � Example: ◦ ◦ � a = [1 2 3 4]; b = [5 6 7 8]; c = a*b Result: ? ? ? Error using ==> mtimes inner matrix dimensions must agree Now, try: ◦ c = a. *b ◦ Result: � %notice the dot! c=[5 12 21 32] Notice what it is doing: a(1)*b(1), a(2)*b(2), etc.

Vector Products Consider & generate two random 3*1 vectors, A & B A=rand(3, 1) , B=rand(3, 1) Dot Product � � Cross Product Check Dimensions � ◦ A*B’ ◦ A’*B By definition � Use MATLAB command >> C=cross(A, B) Use MATLAB command >> C=dot(A, B) � A(2)*B(3)-A(3)*B(2) � A(3)*B(1)-A(1)*B(3) � A(1)*B(2)-A(2)*B(1)

Loops � Loop statements do not need parenthesis. The statements are recognized via tabs. � 3 general types of loops: ◦ If/elseif loops ◦ For loops ◦ While loops � There is a 4 th type, called nested loop, that can be any of the above 3 (and any combinations of them).

If/elseif Loops � The condition must be previously defined!

For Loops Counter variable does not have to be i; it can be any variable � Iterations can be tightly controlled with min: stepsize: max. � � No need to pre-define the counter because you are declaring in the for loop itself! for i=1: 10 statement end

While Loops � As long as output of condition is a logic true, it will continue looping until the condition becomes false. � BE CAREFUL OF INFINITE LOOPS. while condition statement end

Nested Loops Can use a mix of the different types of loops. � Very useful for performing algorithm/operations on vectors and matrices. �

Examples � Write a code to print out integer numbers from 5 to 36 � Write a code to print out integers between 45 to 109 which are divisible to 3 � Write a code to print out integers between 45 to 109 which are divisible to 5 � Write a code : ◦ If n is divisible to 3 print “divisible to 3” ◦ else. If n is divisible to 5 print “divisible to 5” ◦ Elseif n is divisible by 5 and 3 print “divisible by 15”

Section II Feb 6 st, 2016 ◦ Graphing & Plots ◦ Scripts and Functions ◦ Linear & System of Equations Solving

Plots �plot –plot(x, y, linespec) ◦ x and y vectors must be same length! �subplot –subplot(m, n, p) where mxn matrix, p = current graph �figure –creates new window for graph �title –creates text label at top of graph �xlabel/ylabel–horizontal and vertical labels for graph
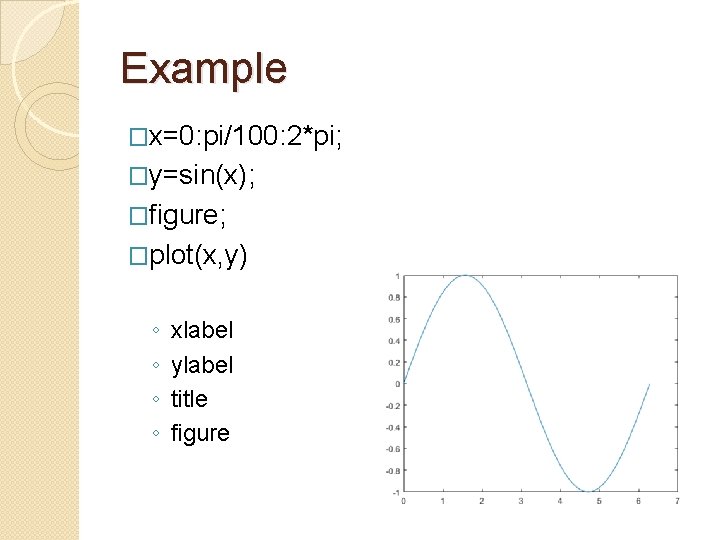
Example �x=0: pi/100: 2*pi; �y=sin(x); �figure; �plot(x, y) ◦ ◦ xlabel ylabel title figure
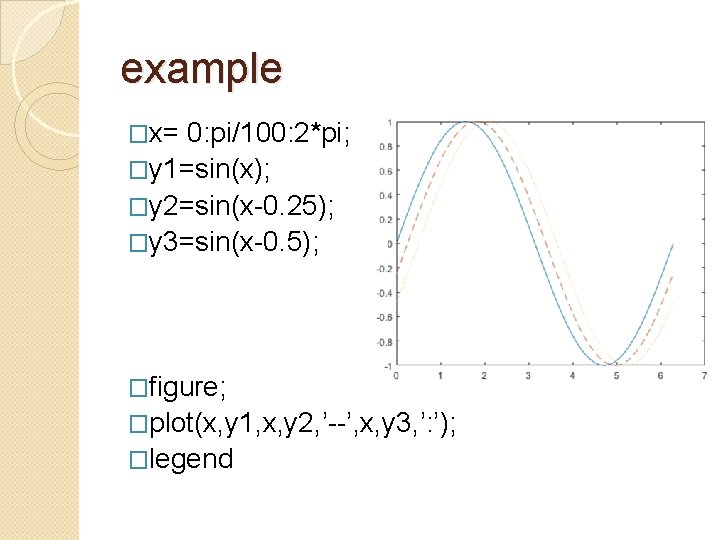
example �x= 0: pi/100: 2*pi; �y 1=sin(x); �y 2=sin(x-0. 25); �y 3=sin(x-0. 5); �figure; �plot(x, y 1, x, y 2, ’--’, x, y 3, ’: ’); �legend
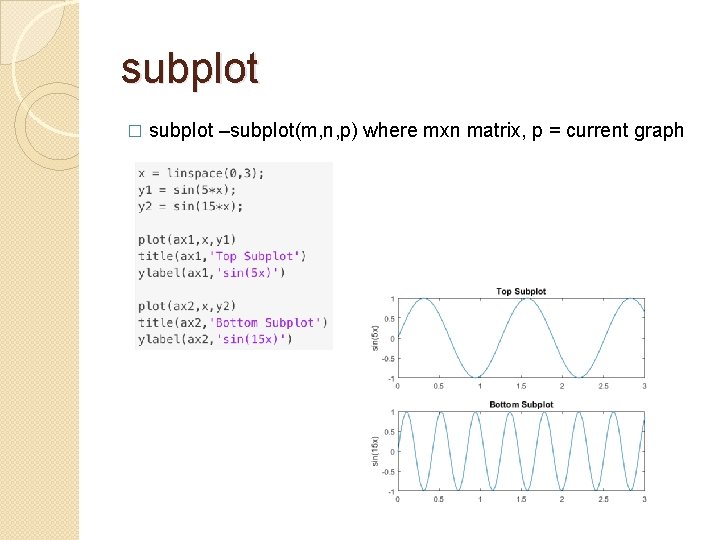
subplot � subplot –subplot(m, n, p) where mxn matrix, p = current graph

Axis-specific Helps focus on what is important on the graph. � Change only the x or y axis limits: ◦ xlim([xminxmax]) or ylim([yminymax]) ◦ min and max can be positive or negative. � example �

Some useful commands � Grid on � Hold on � Legend � Plot 3 ◦ ◦ ◦ : example t=0: pi/50: 10*pi; st=sin(t); ct=cos(t) figure; plot 3(st, ct, t)

plotyy � 2 D line plots with y-axis on both left and right side ◦ [AX, H 1, H 2]=plotyy(x 1, y 1, x 2, y 2)

Scripts & functions �Two kind of M-files: ◦ Scripts ◦ Functions: �With parameters and returning values �Only visible variables defined inside the function or parameters �Usually one file for each function defined �Structure:

Function example �In function: ◦ function y=average(x) ◦ y=sum(x)/length(x); ◦ end �In script: ◦ z=1: 99; ◦ average(z)

Polynomials � We can use an array to represent a polynomial. To do so we use list the coefficients in decreasing order of the powers. For example x 3+4 x+15 will look like [1 0 4 15] � To find roots of this polynomial we use roots command. roots ([1 0 4 15]) � To create a polynomial from its roots poly command is used. poly([1 2 3]) where r 1=1, r 2=2, r 3=3 � To evaluate the new polynomial at x =5 we can use polyval command. polyval([ 1 -6 11 -6], 5)

Systems of Equations � Consider the following system of equations ◦ x+5 y+15 z=7 ◦ x-3 y+13 z=3 ◦ 3 x-4 y-15 z=11 � One way to solve this system of equations is to use matrices. First, define matrix A: ◦ A=[1 5 15; 1 -3 13; 3 -4 15]; � Second, matrix b: ◦ b=[7; 3; 11]; � Third, we solve the equation Ax=b for x, taking the inverse of A and multiply it by b: ◦ x=inv(A)*b � Note that we cannot solve equation Ax=b by dividing b by A because vectors A and b have different dimensions!

Section 3 MATLAB February 20 th, 2016 ◦ Symbolic Solving ◦ Systems of Equations ◦ ODE Solving Farhad Goodarzi

Systems of Equations � Consider the following system of equations ◦ x+5 y+15 z=7 ◦ x-3 y+13 z=3 ◦ 3 x-4 y-15 z=11 � One way to solve this system of equations is to use matrices. First, define matrix A: ◦ A=[1 5 15; 1 -3 13; 3 -4 15]; � Second, matrix b: ◦ b=[7; 3; 11]; � Third, we solve the equation Ax=b for x, taking the inverse of A and multiply it by b: ◦ x=inv(A)*b � Note that we cannot solve equation Ax=b by dividing b by A because vectors A and b have different dimensions!

Symbolic toolbox � Use syms command ◦ syms F 3 x a b ◦ F 3=sqrt(x) ◦ Int(F 3, a, b)

Symbolic toolbox example � Define functions F 1=6 x 3 -4 x 2+bx-5, F 2= Sin (y), and F 3= Sqrt(x). Use int() function to determine:

Solving ODE with dsolve, 1 st order � First order equations ◦ y’=xy �y=dsolve(‘Dy=y*x’, ’x’) �y=dsolve(‘Dy=y*x’, ’y(1)=1’, ’x’) ◦ Or �eq 1=‘Dy=y*x’; �y=dsolve(eq 1, ’x’); ◦ Issues �our expression for y(x) isn’t suited for array operations: vectorize() � y, as MATLAB returns it, is actually a symbol : eval() ◦ Plotting �x = linspace(0, 1, 20); �z = eval(vectorize(y)); �plot(x, z)

Solving ODE with dsolve, 2 nd order � Second order equations ◦ EQ: �eqn 2 = ’D 2 y + 8*Dy + 2*y =cos(x)’; �inits 2 = ’y(0)=0 , Dy(0)=1’; �y=dsolve(eqn 2, inits 2, ’x’) ◦ Plotting �x = linspace(0, 1, 20); �z = eval(vectorize(y)); �plot(x, z)
![Solving ODE with dsolve, systems � Systems of equations ◦ EQs: �[x, y, z]=dsolve(’Dx=x+2*y-z’, Solving ODE with dsolve, systems � Systems of equations ◦ EQs: �[x, y, z]=dsolve(’Dx=x+2*y-z’,](http://slidetodoc.com/presentation_image/46bc8c123d7d31f62a1126fb97b74e8d/image-39.jpg)
Solving ODE with dsolve, systems � Systems of equations ◦ EQs: �[x, y, z]=dsolve(’Dx=x+2*y-z’, ’Dy=x+z’, ’Dz=4*x-4*y+5*z’) �inits=’x(0)=1, y(0)=2, z(0)=3’; �[x, y, z]=dsolve(’Dx=x+2*y-z’, ’Dy=x+z’, ’Dz=4*x-4*y+5*z’, inits) �Notice that since no independent variable was specified, MATLAB used its default, t. ◦ Plotting �t=linspace(0, . 5, 25); �xx=eval(vectorize(x)); �yy=eval(vectorize(y)); �zz=eval(vectorize(z)); �plot(t, xx, t, yy, t, zz)

Solving ODE with dsolve, systems � solve the given differential equations symbolically.

ODE Solving Numerically � Defining an ODE function in an M-file � Solving First-Order ODEs � Solving Systems of First-Order ODEs � Solving higher order ODEs

Numerical methods are used to solve initial value problems where it is difficult to obtain exact solutions �MATLAB has several different built-ins functions for numerical solution of ODEs
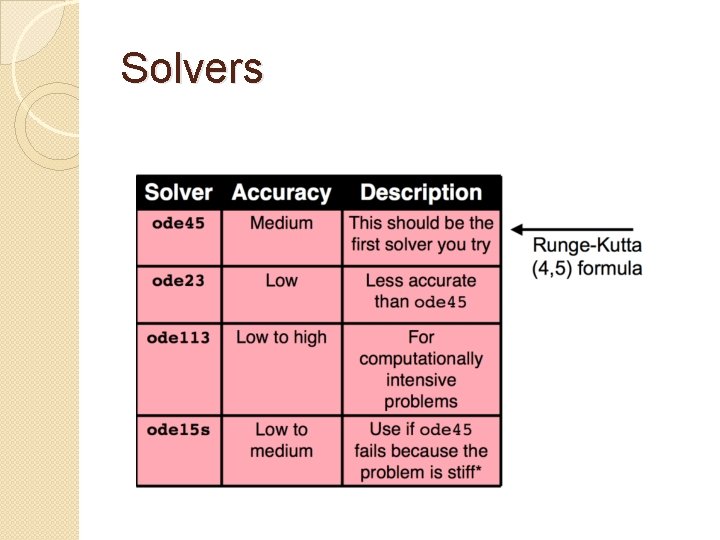
Solvers

Solving first-order ODEs � Define the function M-file � function y_dot=EOM(y, t) � global alpha gamma � y_dot=alpha * y - gamma * y^2; � end � Make a script M-file � global alpha gamma � alpha=0. 15; � gamma=3. 5; � � y 0=1; � [y t]=ode 45(@EOM, [0 10], y 0); � plot(t, y);

Solving systems of ODEs � Example � Create function containing the equations � Change the error tolerance using odeset � Plotting the columns of returned vector

Solving a Stiff system � Equations � Create � Ode the function and plotting

Example � Use “ode 45” to solve the following differential equation and plot y(x) in the interval of [0, 6π]. Put your name in the plot title.
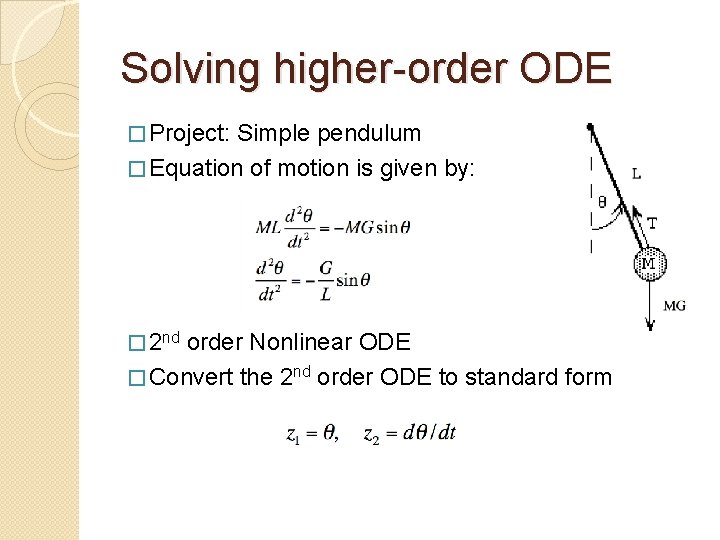
Solving higher-order ODE � Project: Simple pendulum � Equation of motion is given by: � 2 nd order Nonlinear ODE � Convert the 2 nd order ODE to standard form

Simple Pendulum � Initial conditions and constants � Coding ◦ Make a function M-file for equation of motion � function z_dot=EOM_pendulum(t, z) � global G L � theta=z(1); � theta_dot=z(2); � theta_dot 2=-(G/L)*sin(theta); � z_dot=[theta_dot; theta_dot 2]; � end ◦ Make a script M-file to run the code � global G L � G=9. 8; � L=2; � tspan=[0 2*pi]; � inits=[pi/3 0]; � [t, y]=ode 45(@EOM_pendulum, tspan, inits);
![Lorenz Equations � Initials � Plot and constants, T=[0 20] x vs. z , Lorenz Equations � Initials � Plot and constants, T=[0 20] x vs. z ,](http://slidetodoc.com/presentation_image/46bc8c123d7d31f62a1126fb97b74e8d/image-50.jpg)
Lorenz Equations � Initials � Plot and constants, T=[0 20] x vs. z , check if you get same results as

Section 4 March 5 th, 2016 ◦ Simulink
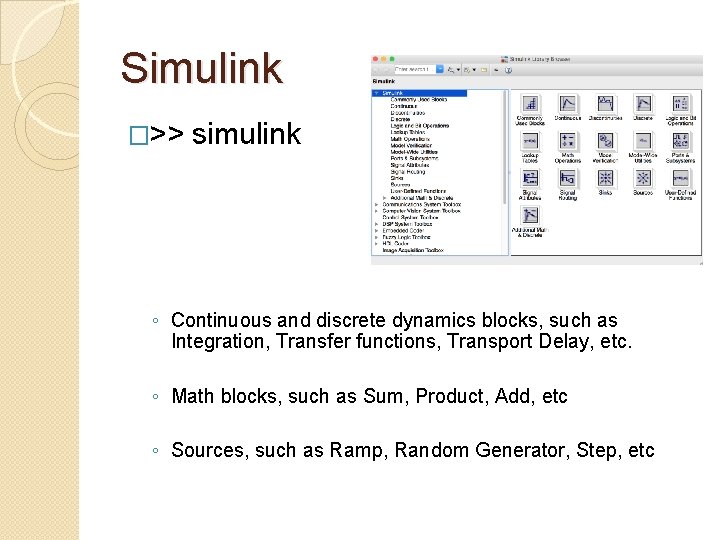
Simulink �>> simulink ◦ Continuous and discrete dynamics blocks, such as Integration, Transfer functions, Transport Delay, etc. ◦ Math blocks, such as Sum, Product, Add, etc ◦ Sources, such as Ramp, Random Generator, Step, etc
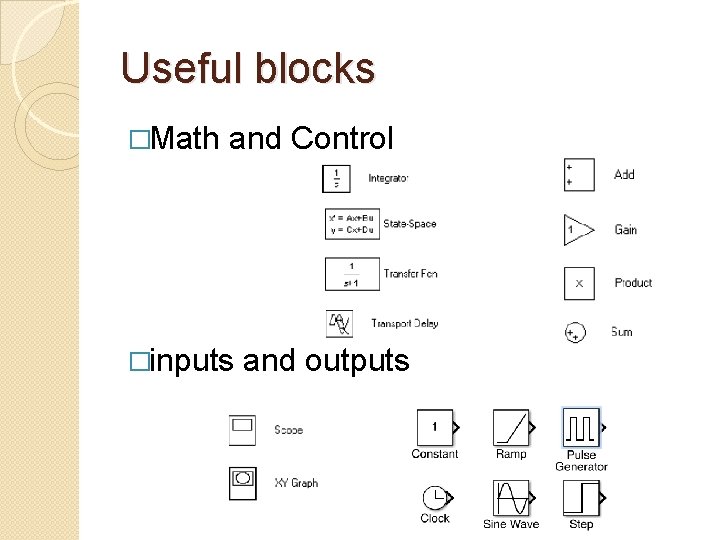
Useful blocks �Math and Control �inputs and outputs
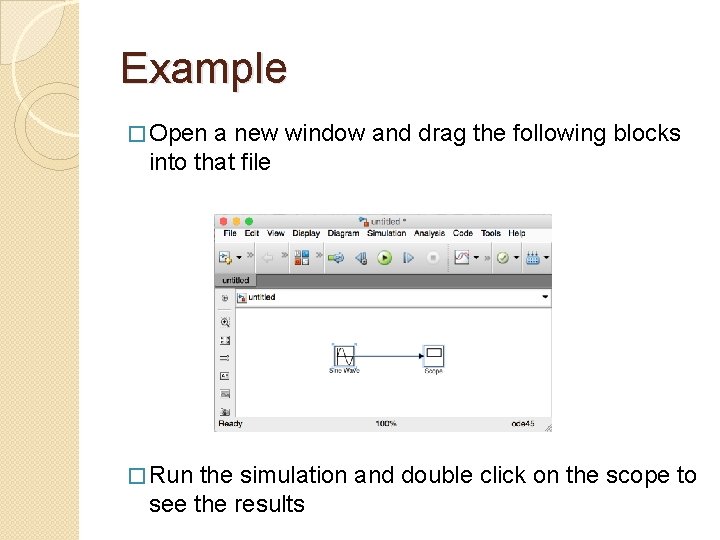
Example � Open a new window and drag the following blocks into that file � Run the simulation and double click on the scope to see the results
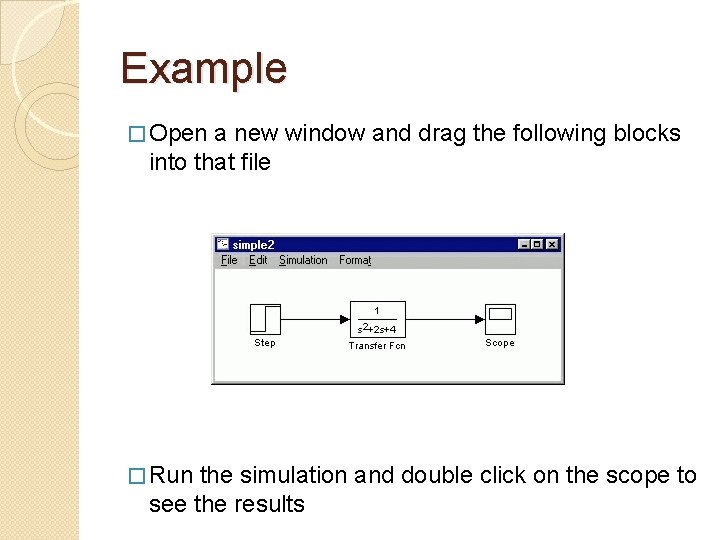
Example � Open a new window and drag the following blocks into that file � Run the simulation and double click on the scope to see the results
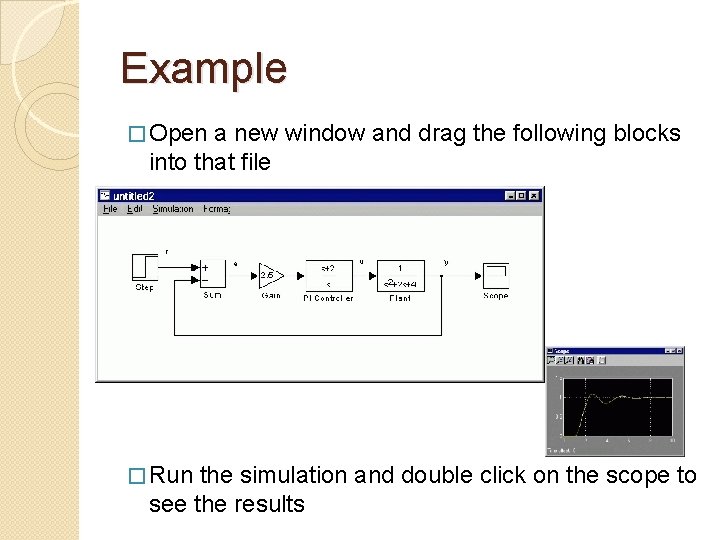
Example � Open a new window and drag the following blocks into that file � Run the simulation and double click on the scope to see the results

simple model � Build a Simulink model that solves the differential equation � Initial condition � First, sketch a simulation diagram of this mathematical model (equation) � Input is the forcing function 3 sin(2 t) � Output is the solution of the differential equation x(t)

simple model � Build a Simulink model that solves the differential equation Double-click on the Sine Wave block to set amplitude = 3 and freq = 2. This produces the desired input of 3 sin(2 t)
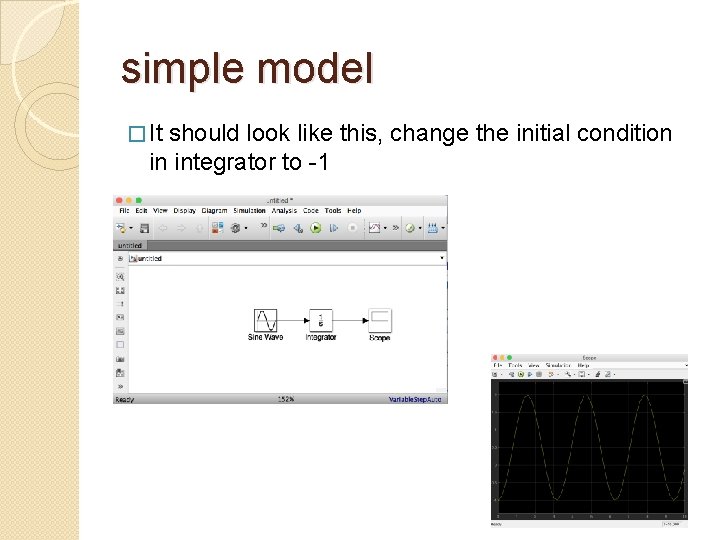
simple model � It should look like this, change the initial condition in integrator to -1

Example – Toy Train � consisting of an engine and a car. Assuming that the train only travels in one direction, we want to apply control to the train so that it has a smooth start-up and stop, along with a constant-speed ride � The mass of the engine and the car will be represented by M 1 and M 2, respectively. The two are held together by a spring, which has the stiffness coefficient of k. F represents the force applied by the engine, and the Greek letter, mu, represents the coefficient of rolling friction.

Example – Toy Train �System

Example – Toy Train �System
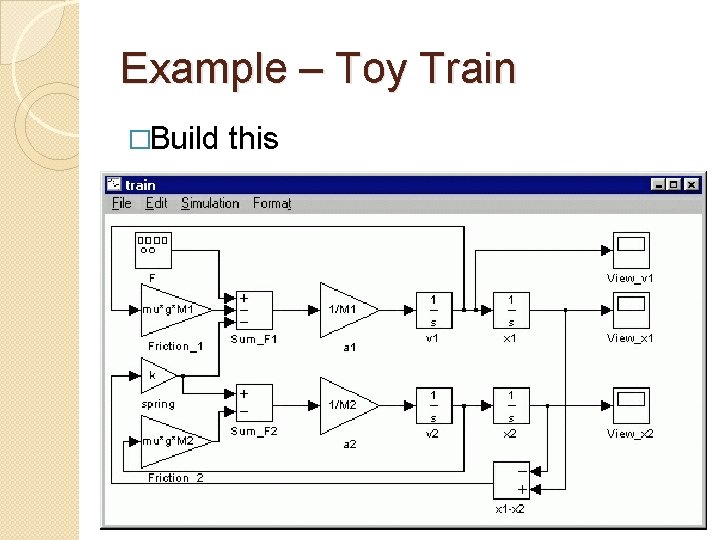
Example – Toy Train �Build this

Example – Toy Train � Before running the model, we need to assign numerical values to each of the variables used in the model. Create an new m-file and enter the following commands. � M 1=1; � M 2=0. 5; � k=1; � F=1; � mu=0. 002; � g=9. 8; � Execute your m-file to define these values. Simulink will recognize MATLAB variables for use in the model.

Pendulum Example �Try the following blocks
- Slides: 65