Control Example using Matlab Cruise Control Modeling a

Control Example using Matlab Cruise Control

Modeling a Cruise Control System Physical setup and system equations • The inertia of the wheels is neglected • Aerodynamic Drag is neglected – is proportional to the square of the car’s speed • It is assumed that friction is opposing the motion of the car –is proportional to the car's speed • The problem is reduced to the simple mass and damper system

Modeling a Cruise Control System • Using Newton's law, the dynamic equation for this system is: where u is the force from the engine. • There are several different ways to describe a system of linear differential equations. • To calculate the Transfer Function, we shall use the Stare Space representation then transform it to TF using ss 2 tf

State-space equations • The state-space representation is given by the equations: where is an n by 1 vector representing the state (commonly position and velocity variables in mechanical systems), u is a scalar representing the input (commonly a force or torque in mechanical systems), and y is a scalar representing the output.

State Equation for our CC model The state vector The equation or is [ x, ] and y is is

Design requirements • For this example, let's assume that m = 1000 kg b = 50 Nsec/m u = 500 N • Design requirements – When the engine gives a 500 Newton force, the car will reach a maximum velocity of 10 m/s (22 mph). – An automobile should be able to accelerate up to that speed in less than 5 seconds. Since this is only a cruise control system, a 10% overshoot on the velocity will not do much damage. A 2% steadystate error is also acceptable for the same reason. – Rise time < 5 sec Overshoot < 10% Steady state error < 2%
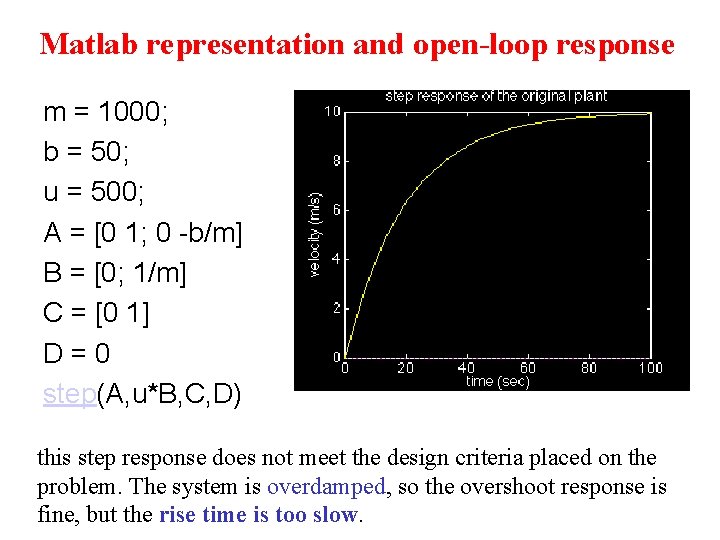
Matlab representation and open-loop response m = 1000; b = 50; u = 500; A = [0 1; 0 -b/m] B = [0; 1/m] C = [0 1] D=0 step(A, u*B, C, D) this step response does not meet the design criteria placed on the problem. The system is overdamped, so the overshoot response is fine, but the rise time is too slow.

P controller • The first thing to do in this problem is to transform the statespace equations into transfer function form. m = 1000; b = 50; u = 500; A = [0 1; 0 -b/m] B = [0; 1/m] C = [0 1] D = 0 [num, den]=ss 2 tf(A, B, C, D) • Next, close the loop and add some proportional control to see if the response can be improved. k = 100; [numc, denc] = cloop(k*num, den, -1); %Closed-loop transfer function t = 0: 0. 1: 20; step(10*numc, denc, t) %for 10 m/sec the signal used by step axis([0 20 0 10])

Get the Transfer Function • For m = 1000; b = 50; u = 500; A = [0 1; 0 -b/m] B = [0; 1/m] C = [0 1] D = 0 [num, den]=ss 2 tf(A, B, C, D) • Matlab should return the following to the command window: num = 0 0. 0010 0 1. 0000 0. 0500 0 den = • This is the way Matlab presents the TF 0. 001 s + 0 ---------s^2 + 0. 05 s + 0

Step function • The step function is one of most useful functions in Matlab for control design. • Given a system that can be described by either a transfer function or a set of state-space equations, the response to a step input can immediately be plotted. • A step input can be described as a change in the input from zero to a finite value at time t = 0. • By default, the step command performs a unit step (i. e. the input goes from zero to one at time t = 0). • The basic command to use the step function is one of the following – (depending if you have a set of state-space equations or a transfer function form): step(A, B, C, D) step(num, den)

P controller • The steady state error is more than 10%, and the rise time is still too slow. • Adjust the proportional gain to make the response better. v but you will not be able to make the steady state value go to 10 m/sec without getting rise times that are too fast. • You must always keep in mind that you are designing a real system, and for a cruise control system to respond 0 -10 m/sec in less than half of a second is unrealistic. • To illustrate this idea, adjust the k value to equal 10, 000, and you should get the following velocity response:
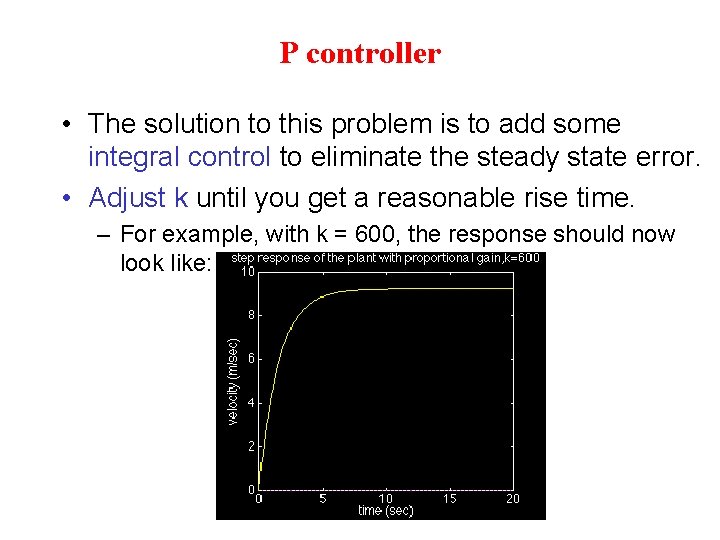
P controller • The solution to this problem is to add some integral control to eliminate the steady state error. • Adjust k until you get a reasonable rise time. – For example, with k = 600, the response should now look like:

PI controller Remember, integral control makes the transient response worse, so adding too much initially can make the response unrecognizable. k = 600; ki = 1; % small to get feeling for integral response num 1 = [k ki]; % PI has two gains den 1 = [1 0]; num 2 = conv(num, num 1); % convolution used to multiply the % polynomials representing the gains den 2 = conv(den, den 1); [numc, denc] = cloop(num 2, den 2, -1); t = 0: 0. 1: 20; step(10*numc, denc, t)
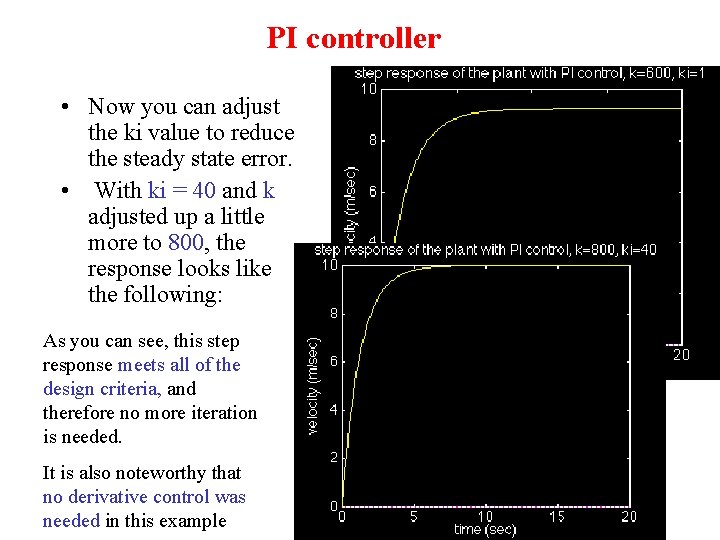
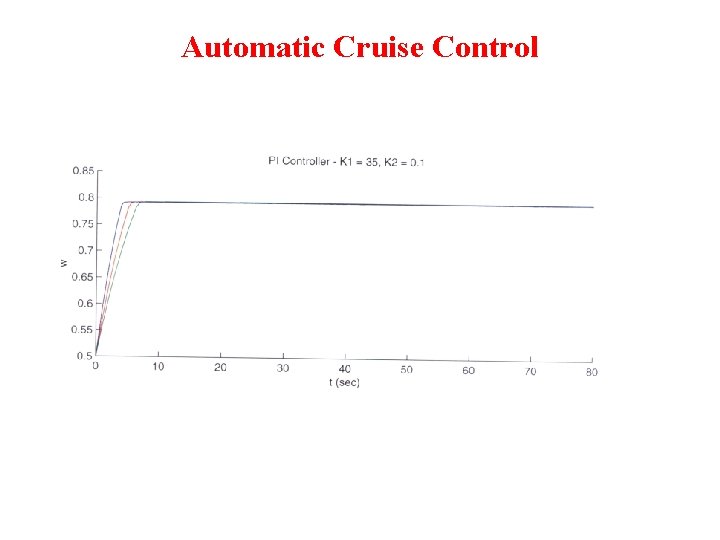
PI controller • Now you can adjust the ki value to reduce the steady state error. • With ki = 40 and k adjusted up a little more to 800, the response looks like the following: As you can see, this step response meets all of the design criteria, and therefore no more iteration is needed. It is also noteworthy that no derivative control was needed in this example

Modeling a Cruise Control System Physical setup and system equations Let’s now add Drag and assume the friction to be non velocity dependent (the static friction, proportional to normal force). מסת המכונית - M מקדם חיכוך - B כח המנוע של המכונית - C . • כוח האינרציה שווה לכוח המניע פחות כוח החיכוך : כלומר : וכאשר

Very Short Simulink Tutorial • In the Matlab command window write simulink. • The window that has opened is the Simulink Library Browser. – It is used to choose various Simulink modules to use in your simulation. • From this window, choose the File menu, and then New (Model). – Now we have a blank window, in which we will build our model. – This blank window and the library browser window, will be the windows we’ll work with. • We choose components from the library browser, and then drag them to our work window. – We’ll use only the Simulink library (also called toolbox) for now.
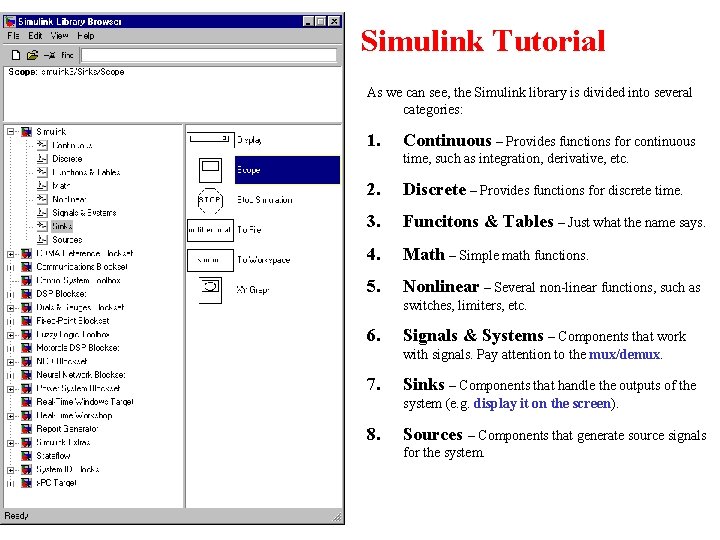
Simulink Tutorial As we can see, the Simulink library is divided into several categories: 1. Continuous – Provides functions for continuous time, such as integration, derivative, etc. 2. Discrete – Provides functions for discrete time. 3. Funcitons & Tables – Just what the name says. 4. Math – Simple math functions. 5. Nonlinear – Several non-linear functions, such as switches, limiters, etc. 6. Signals & Systems – Components that work with signals. Pay attention to the mux/demux. 7. Sinks – Components that handle the outputs of the system (e. g. display it on the screen). 8. Sources – Components that generate source signals for the system.
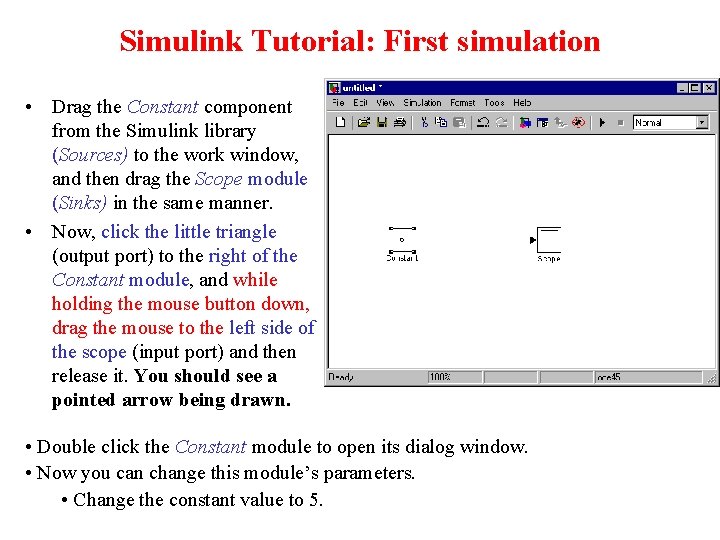
Simulink Tutorial: First simulation • Drag the Constant component from the Simulink library (Sources) to the work window, and then drag the Scope module (Sinks) in the same manner. • Now, click the little triangle (output port) to the right of the Constant module, and while holding the mouse button down, drag the mouse to the left side of the scope (input port) and then release it. You should see a pointed arrow being drawn. • Double click the Constant module to open its dialog window. • Now you can change this module’s parameters. • Change the constant value to 5.
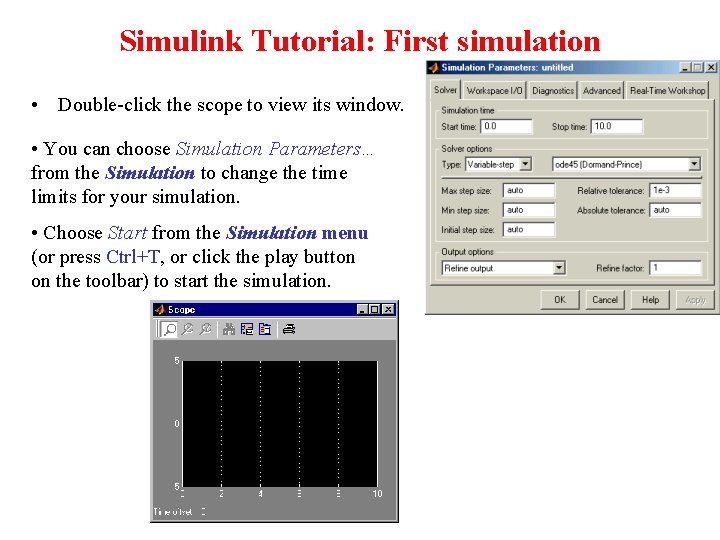
Simulink Tutorial: First simulation • Double-click the scope to view its window. • You can choose Simulation Parameters… from the Simulation to change the time limits for your simulation. • Choose Start from the Simulation menu (or press Ctrl+T, or click the play button on the toolbar) to start the simulation.
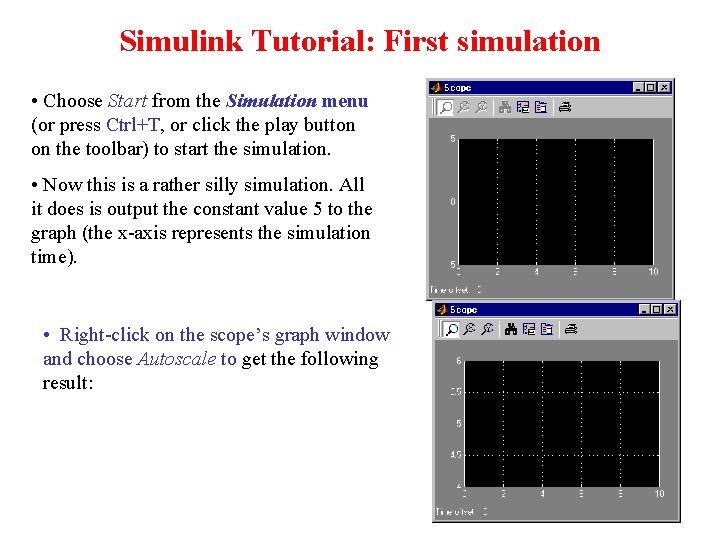
Simulink Tutorial: First simulation • Choose Start from the Simulation menu (or press Ctrl+T, or click the play button on the toolbar) to start the simulation. • Now this is a rather silly simulation. All it does is output the constant value 5 to the graph (the x-axis represents the simulation time). • Right-click on the scope’s graph window and choose Autoscale to get the following result:
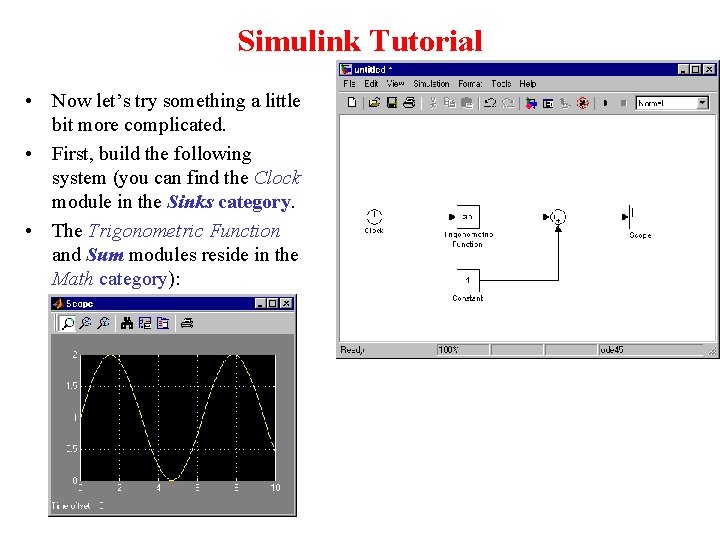
Simulink Tutorial • Now let’s try something a little bit more complicated. • First, build the following system (you can find the Clock module in the Sinks category. • The Trigonometric Function and Sum modules reside in the Math category):
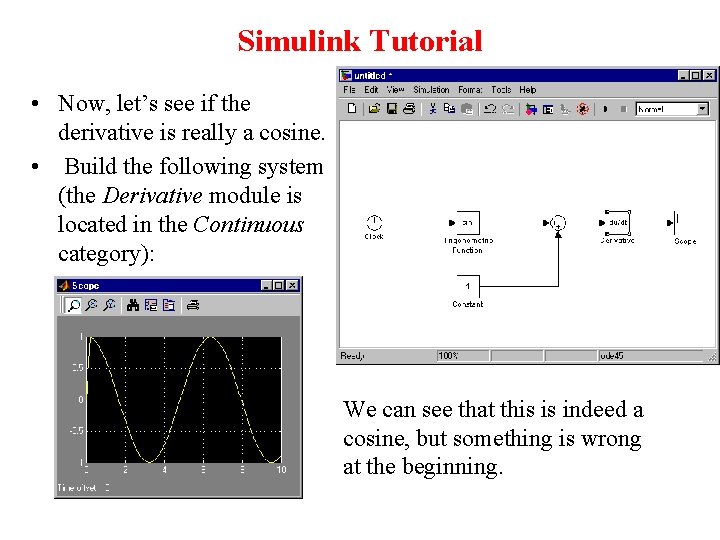
Simulink Tutorial • Now, let’s see if the derivative is really a cosine. • Build the following system (the Derivative module is located in the Continuous category): We can see that this is indeed a cosine, but something is wrong at the beginning.
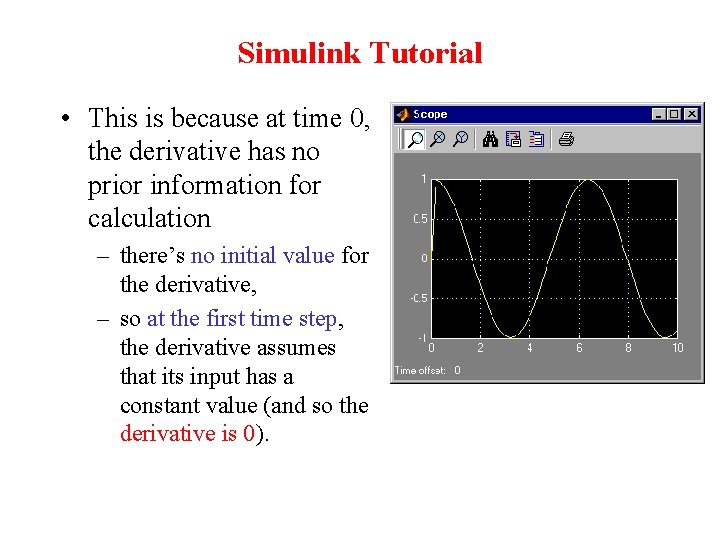
Simulink Tutorial • This is because at time 0, the derivative has no prior information for calculation – there’s no initial value for the derivative, – so at the first time step, the derivative assumes that its input has a constant value (and so the derivative is 0).

An other example • Let’s say that we have a differential equation that we want to model. The equation is: • How can we solve this numerically using Simulink? We’ll notice 2 simple facts: 1. If we have A, then we have A' (multiplication). 2. If we have A', then we have A (integration). We can get out of this loop by using the initial condition. We know that A 0 = 0. 5, so now we can calculate A' and then recalculate the new A, and so on.
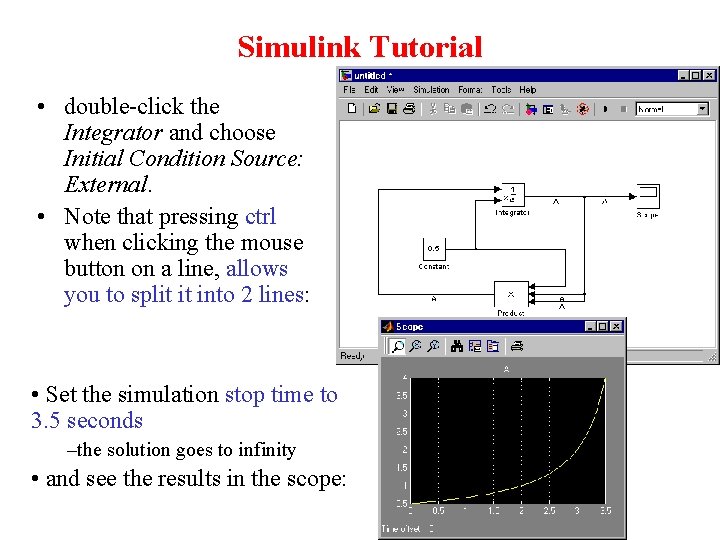
Simulink Tutorial • double-click the Integrator and choose Initial Condition Source: External. • Note that pressing ctrl when clicking the mouse button on a line, allows you to split it into 2 lines: • Set the simulation stop time to 3. 5 seconds –the solution goes to infinity • and see the results in the scope:
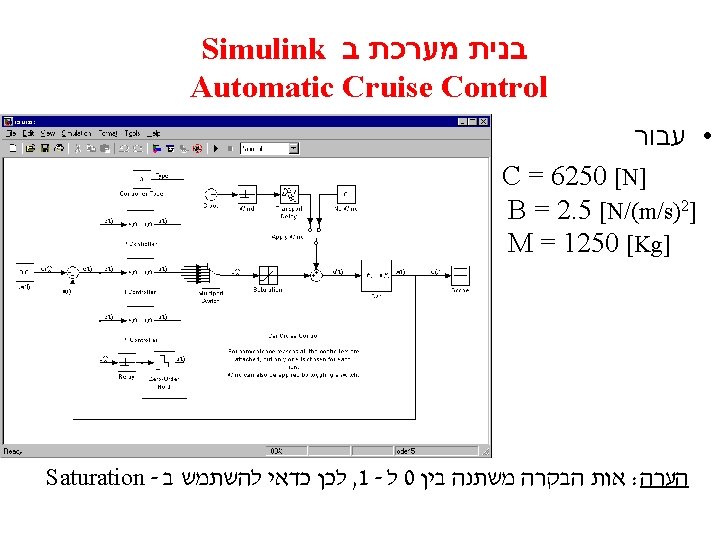
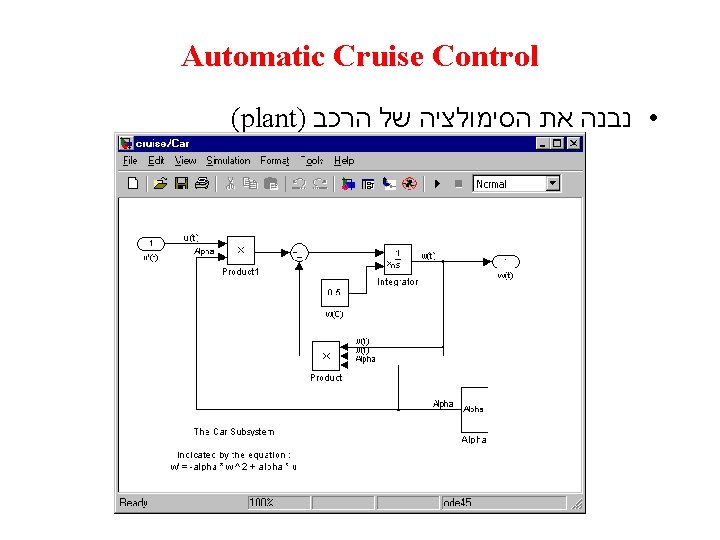
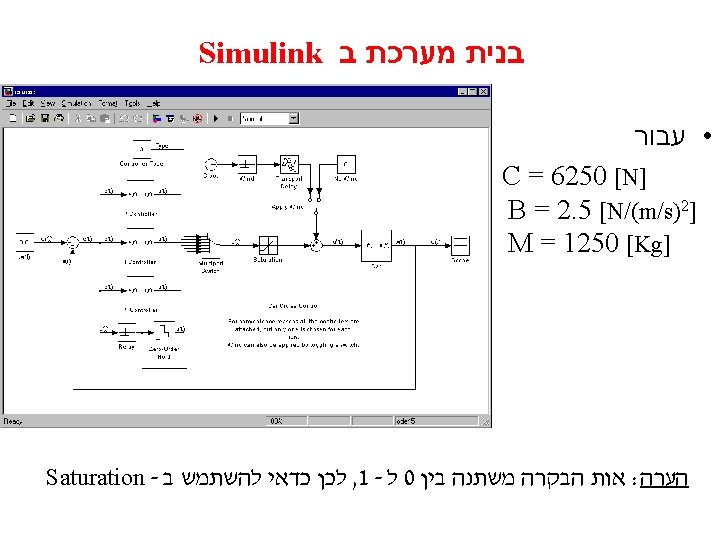
Automatic Cruise Control (plant) • נבנה את הסימולציה של הרכב
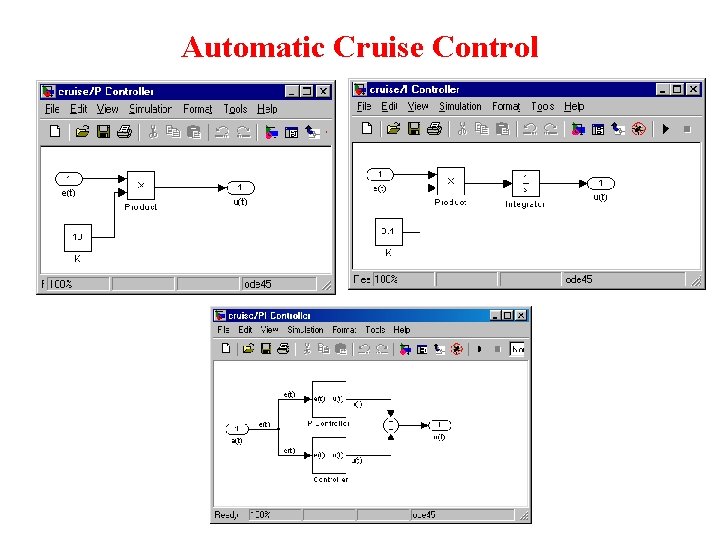
Automatic Cruise Control

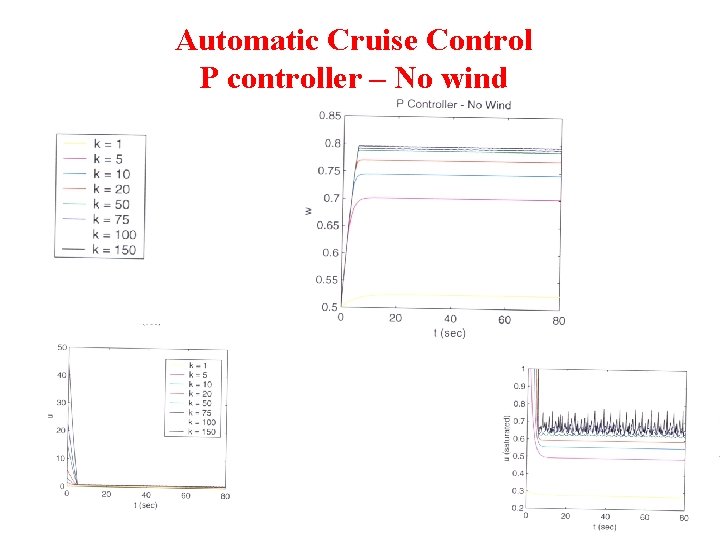
Automatic Cruise Control P controller – No wind
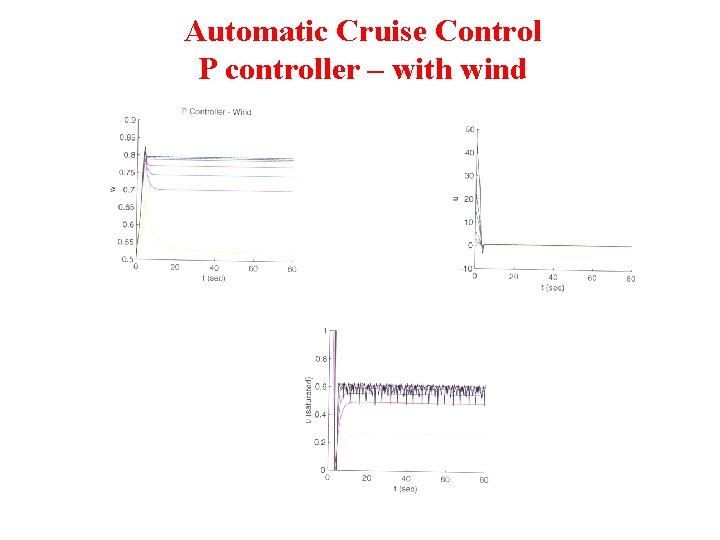
Automatic Cruise Control P controller – with wind
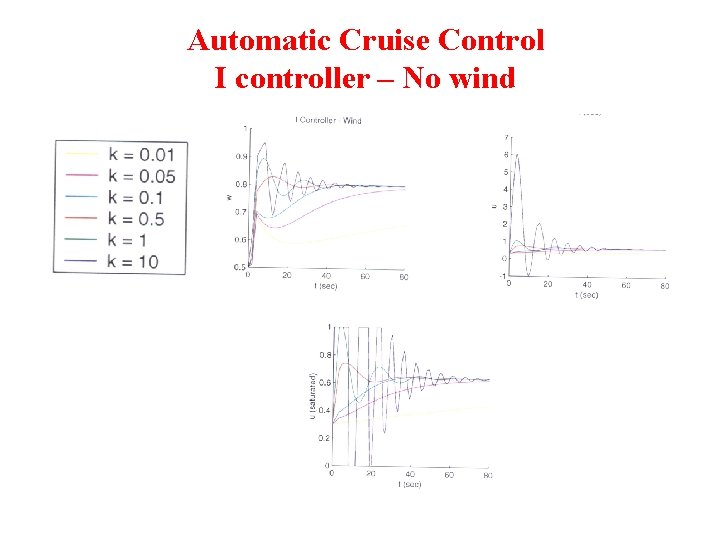
Automatic Cruise Control I controller – No wind
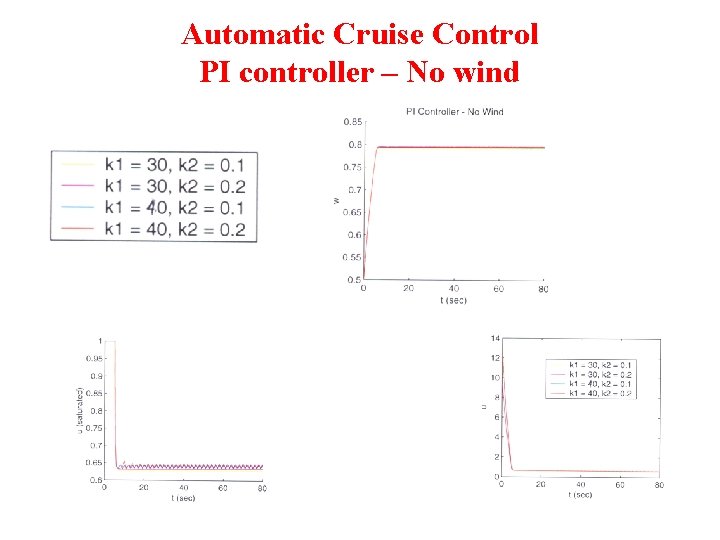
Automatic Cruise Control PI controller – No wind

Automatic Cruise Control PI controller – with wind
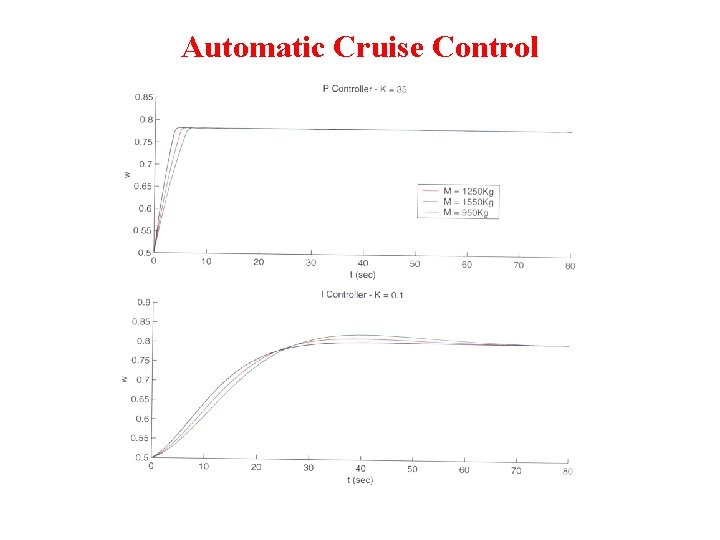
Automatic Cruise Control
Automatic Cruise Control
- Slides: 37