The Dot Product The dot product F G

The Dot Product The dot product F ·G of F and G is the real number formed by multiplying the two first components, then the two second components, then the two third components, and adding these three numbers. If F=a 1 i+b 1 j+c 1 k and G=a 2 i+b 2 j+c 2 k, then F ·G=a 1 a 2 +b 1 b 2 +c 1 c 2. Again, this dot product is a number, not a vector. For example,

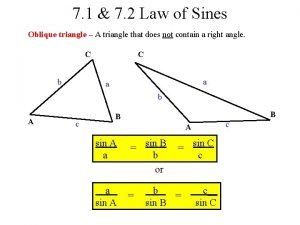
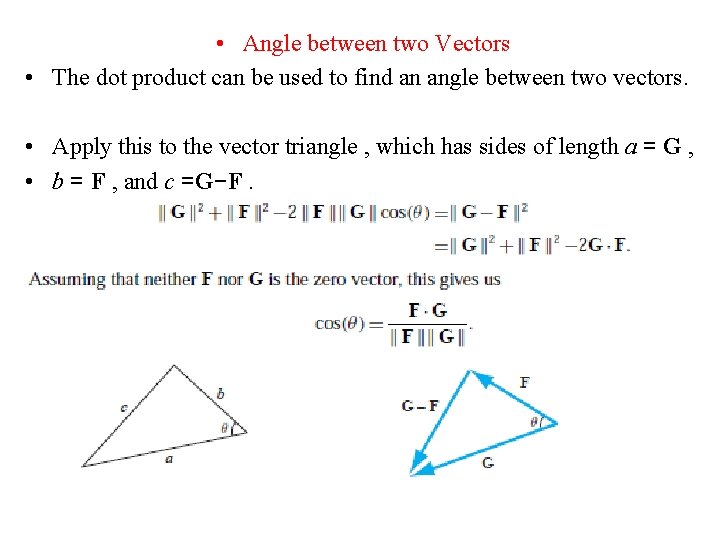
• Angle between two Vectors • The dot product can be used to find an angle between two vectors. • Apply this to the vector triangle , which has sides of length a = G , • b = F , and c =G−F.

• Orthogonal Vectors • Two nonzero vectors F and G are orthogonal (perpendicular) when • the angle θ between them is π/2 radians. This happens exactly when • cos(θ)=0= F ·G • which occurs when F ·G=0. It is convenient to also agree that O is orthogonal to every vector. With this convention, two vectors are orthogonal if and only if their dot product is

• EXAMPLE 6. 4 • Let F=− 4 i+j+2 k, G=2 i+4 k and H=6 i−j− 2 k. • • Then F ·G=0, so F and G are orthogonal. • But F · H and G · H are not zero, so F and H are not orthogonal and G and H are not • orthogonal.

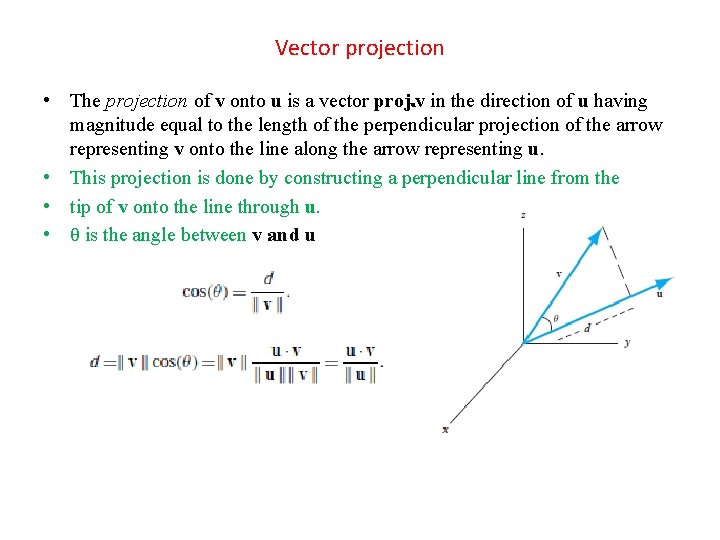
Vector projection • The projection of v onto u is a vector proj v in the direction of u having magnitude equal to the length of the perpendicular projection of the arrow representing v onto the line along the arrow representing u. • This projection is done by constructing a perpendicular line from the • tip of v onto the line through u. • θ is the angle between v and u u

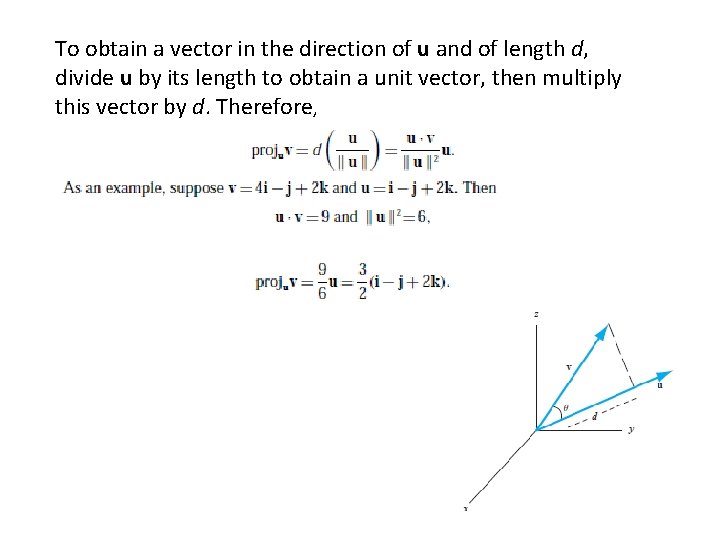
To obtain a vector in the direction of u and of length d, divide u by its length to obtain a unit vector, then multiply this vector by d. Therefore,

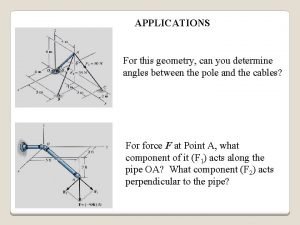
• Orthogonality is also useful for determining the equation of a plane in 3 -space. • Any plane has an equation of the form ax +by +cz =d. • As suggested by Figure 6. 12, if we specify a point on the plane and a vector orthogonal to the plane, then the plane is completely determined. • This strategy is explained in the following example

• Example: • We will find the equation of the plane P containing the point (− 6, 1, 1) and orthogonal to the vector N=− 2 i + 4 j + k. Such a vector N is said to be normal to P and is called a normal vector to P. • Here is a strategy. Because (− 6, 1, 1) is on P, a point (x, y, z) is on P exactly when the vector between (− 6, 1, 1) and (x, y, z) lies in P. But then (x +6)i+(y − 1)j+(z − 1)k must • be orthogonal to N, so N· ((x +6)i+(y − 1)j+(z − 1)k)=0. • Then • − 2(x +6)+4(y − 1)+(z − 1)=0, • or • − 2 x +4 y +z =17. • This is the equation of P.

• Problems A. In each of Problems 1 through 6, compute the dot product of the vectors and the cosine of the angle between them. Also determine if the vectors are orthogonal. • • • 1. i, 2 i− 3 j+k 2. 2 i− 6 j+k, i−j 3. − 4 i− 2 i+3 k, 6 i− 2 j−k 4. 8 i− 3 j+2 k, − 8 i− 3 j+k 5. i− 3 k, 2 j+6 k 6. i+j+2 k, i−j+2 k

• B. find the equation of the plane containing the given point and orthogonal • • • to the given vector. 7. (− 1, 1, 2), 3 i−j+4 k 8. ( − 1, 0, 0), i− 2 j 9. (2, − 3, 4), 8 i− 6 j+4 k 10. (− 1, − 5), − 3 i+2 j 11. (0, − 1, 4), 7 i+6 j− 5 k 12. ( − 2, 1, − 1), 4 i+3 j+k • C. Find the projection of v onto u. • 13. v=i−j+4 k, u=− 3 i+2 j−k • 14. v=5 i+2 j− 3 k, u=i− 5 j+2 k • 15. v=−i+3 j+6 k, u=2 i+7 j− 3 k

• CROSS PRODUCT • The dot produces a scalar from two vectors. • The cross product produces a vector from two vectors. • Let F=a i+b j+c k and G=a i+b j+c k. The cross product of F with G is the vector F×G defined by • F×G = (b c −b c ) i+(a c −a c ) j+(a b −a b ) k. • Here is a simple device for remembering and computing these components. Form the determinant: 1 1 1 2 1 2 2 1 1 2 2 2 1

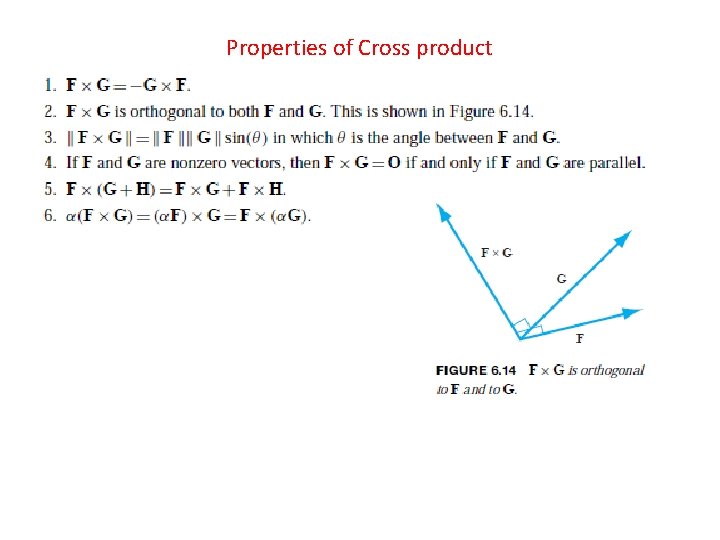
Properties of Cross product

• Property (1) of the cross product follows from the fact that interchanging two rows of a determinant changes its sign. In computing F×G, the components of F are in the second row of the determinant, and those of G in the third row. These rows are interchanged in computing G×F. • For property (2), compute the dot product F · • (F×G) =a [b c −b c ]+b [a c −a c ]+c [a b −a b ]=0. Therefore, F is orthogonal to F×G. Similarly, G is orthogonal to F×G. 1 1 2 2 1 1 2 2 1 • To derive property (3), suppose both vectors are nonzero and recall that • where θ is the angle between F and G. Now write

Problems A. compute F×G and G×F 1. F=− 3 i+6 j+k, G=−i− 2 j+k 2. F=6 i−k, G=j+2 k 3. F=2 i− 3 j+4 k, G=− 3 i+2 j 4. F=8 i+6 j, G=14 j

The Vector Space

• Example