FiveMinute Check over Lesson 8 4 ThenNow New

Five-Minute Check (over Lesson 8 -4) Then/Now New Vocabulary Key Concept: Dot Product and Orthogonal Vectors in Space Example 1: Find the Dot Product to Determine Orthogonal Vectors in Space Example 2: Angle Between Two Vectors in Space Key Concept: Cross Product of Vectors in Space Example 3: Find the Cross Product of Two Vectors Example 4: Real-World Example: Torque Using Cross Product Example 5: Area of a Parallelogram in Space Key Concept: Triple Scalar Product Example 6: Volume of a Parallelepiped

Over Lesson 8 -4 Find the length and the midpoint of the segment with endpoints at (− 2, 3, 4) and (6, 1, − 5). A. 8. 31; B. 10. 04; C. 12. 21; D. 12. 21;

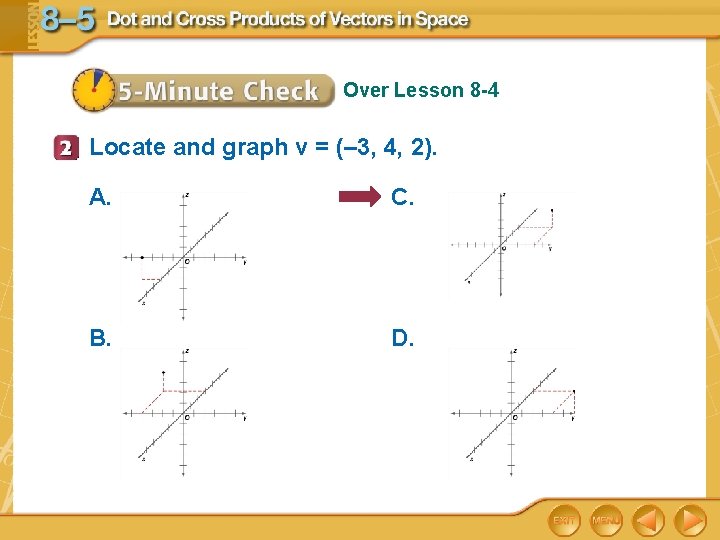
Over Lesson 8 -4 Locate and graph v = (– 3, 4, 2). A. C. B. D.

Over Lesson 8 -4 Which of the following represents 3 x – 5 y + z if x = 2, – 7, 1 , y = – 5, 0, 3 , and z = – 1, 6, – 4 ? A. – 23, – 15, 14 B. 6, – 1, – 6 C. 30, − 15, − 16 D. 30, − 15, 14

You found the dot product of two vectors in the plane. (Lesson 8 -3) • Find dot products of and angles between vectors in space. • Find cross products of vectors in space and use cross products to find area and volume.

• cross product • torque • parallelepiped • triple scalar product

Find the Dot Product to Determine Orthogonal Vectors in Space A. Find the dot product of u and v for u = – 1, 6, – 3 and v = 3, – 1, – 3. Then determine if u and v are orthogonal. u • v = – 1(3) + 6(– 1) + (– 3) = – 3 + (– 6) + 9 or 0 Since u • v = 0, u and v are orthogonal. Answer: 0; orthogonal

Find the Dot Product to Determine Orthogonal Vectors in Space B. Find the dot product of u and v for u = 2, 4, – 6 and v = – 3, 2, 4. Then determine if u and v are orthogonal. u • v = 2(– 3) + 4(2) + (– 6)(4) = – 6 + 8 + (– 24) or – 22 Since u • v ≠ 0, u and v are not orthogonal. Answer: – 22; not orthogonal

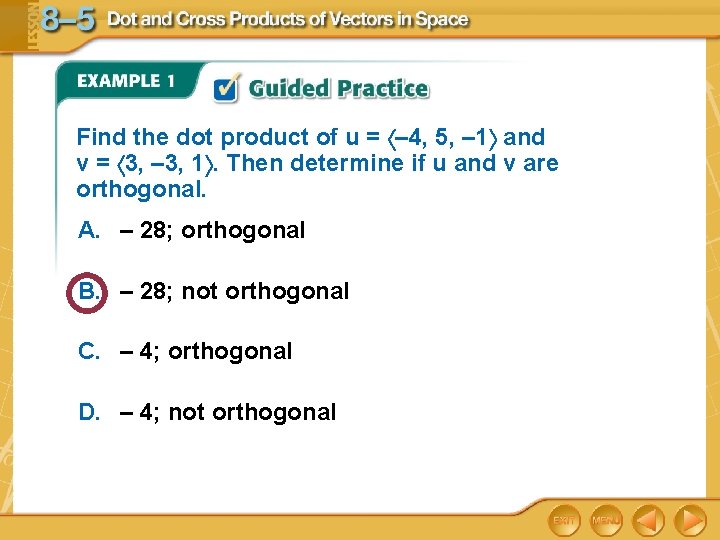
Find the dot product of u = – 4, 5, – 1 and v = 3, – 3, 1. Then determine if u and v are orthogonal. A. – 28; orthogonal B. – 28; not orthogonal C. – 4; orthogonal D. – 4; not orthogonal

Angle Between Two Vectors in Space Find the angle θ between u = – 4, – 1, – 3 and v = 7, 3, 4 to the nearest tenth of a degree. Angle between two vectors u = – 4, – 1, – 3 and v = 7, 3, 4 Evaluate the dot product and magnitudes.

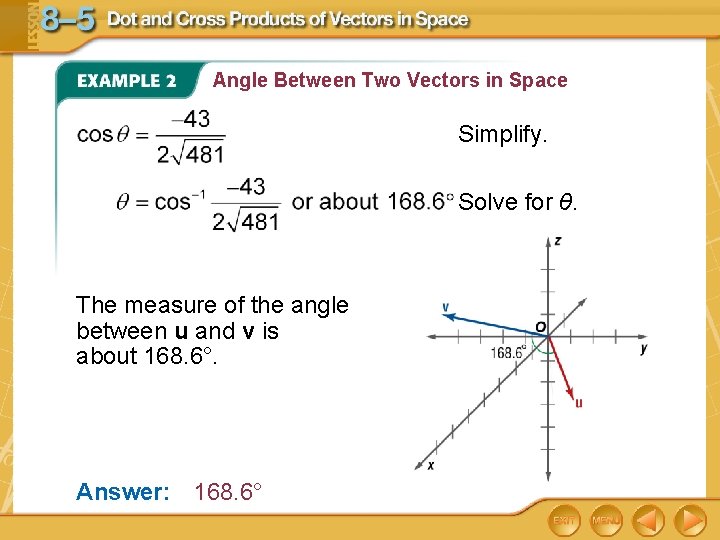
Angle Between Two Vectors in Space Simplify. Solve for θ. The measure of the angle between u and v is about 168. 6°. Answer: 168. 6°

Find the angle between u = – 2, 3, – 1 and v = – 4, – 3, 4 to the nearest tenth of a degree. A. 12. 0° B. 78. 0° C. 82. 8° D. 102. 0°

Find the Cross Product of Two Vectors Find the cross product of u = 6, – 1, – 2 and v = – 1, – 4, 2. Then show that u × v is orthogonal to both u and v. u = 6, – 1, – 2 and v = – 1, – 4, 2 Determinant of a 3 × 3 matrix Determinants of 2 × 2 matrices

Find the Cross Product of Two Vectors Simplify. Component form To show that u × v is orthogonal to both u and v, find the dot product of u × v with u and u × v with v. (u × v) • u = – 10, – 25 • 6, – 1, – 2 = – 10(6) + (– 10)(– 1) + (– 25)( – 2) = – 60 + 10 + 50 or 0

Find the Cross Product of Two Vectors (u × v) • v = – 10, – 25 • – 1, – 4, 2 = – 10(– 1) + (– 10)(– 4) + (– 25)( 2) = 10 + 40 + (– 50) or 0 Because both dot products are zero, the vectors are orthogonal. Answer: – 10, – 25 ; u×v • u = – 10, – 25 • 6, – 1, – 2 = – 60 + 10 + 50 = 0 u×v • v = – 10, – 25 • – 1, – 4, 2 = 10 + 40 – 50 = 0

Find the cross product of u = 2, 3, – 1 and v = – 3, 1, 4. A. u × v = 13, 5, 11 B. u × v = 13, – 5, 11 C. u × v = 12, – 5, 7 D. u × v = 13, 5, 11

Torque Using Cross Product MACHINERY A mechanic uses a 0. 4 -meter long wrench to tighten a nut. Find the magnitude and direction of the torque about the nut if the force is 30 newtons straight down to the end of the handle when it is 35° above the positive x-axis. Step 1 Graph each vector in standard position.

Torque Using Cross Product Step 2 Determine the component form of each vector. The component form of the vector representing the directed distance from the axis of rotation to the end of the handle can be found using the triangle in the figure below and trigonometry.

Torque Using Cross Product Vector r is therefore 0. 4 cos 35°, 0, 0. 4 sin 35° or about 0. 33, 0, 0. 23. The vector representing the force applied to the end of the handle is 30 newtons straight down, so F = 0, 0, – 30. Step 3 Use the cross product of these vectors to find the vector representing the torque about the nut. T=r×F Torque Cross Product Formula Cross product of r and F

Torque Using Cross Product Determinant of a 3 × 3 matrix Determinants of 2 × 2 matrices Component form

Torque Using Cross Product Step 4 Find the magnitude and direction of the torque vector. The component form of the torque vector 0, 9. 9, 0 tells us that the magnitude of the vector is about 9. 9 newton-meters parallel to the positive y-axis as shown below. Answer: 9. 9 N • m parallel to the positive y-axis

MACHINERY A mechanic uses a 0. 3 -meter-long wrench to tighten a nut. Find the magnitude and direction of the torque about the nut if the force is 35 newtons straight down to the end of the handle when it is 40° below the positive x-axis as shown below. A. 10. 5 N • m parallel to the positive y-axis B. 8. 0 N • m parallel to the positive y-axis C. 6. 7 N • m parallel to the positive y-axis D. 4. 1 N • m parallel to the positive y-axis

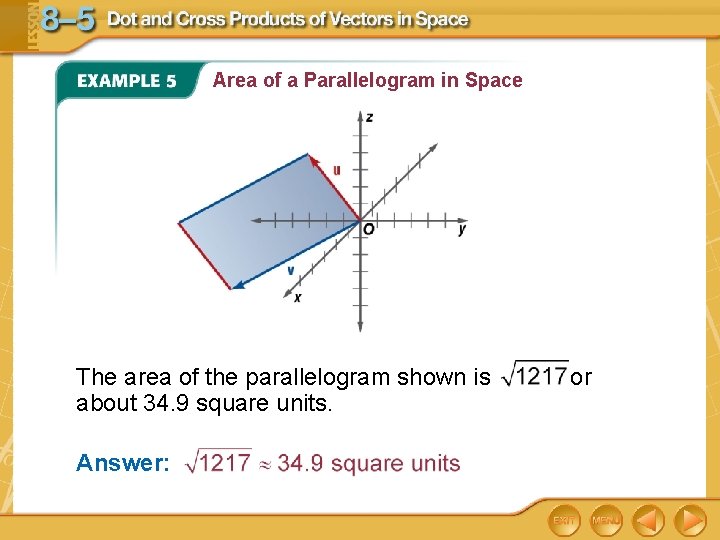
Area of a Parallelogram in Space Find the area of the parallelogram with adjacent sides u = – 3 i – 4 j +2 k and v = 5 i – 4 j – k. Step 1 Find u × v. u = – 3 i – 4 j +2 k and v = 5 i – 4 j – k Determinant of a 3 × 3 matrix

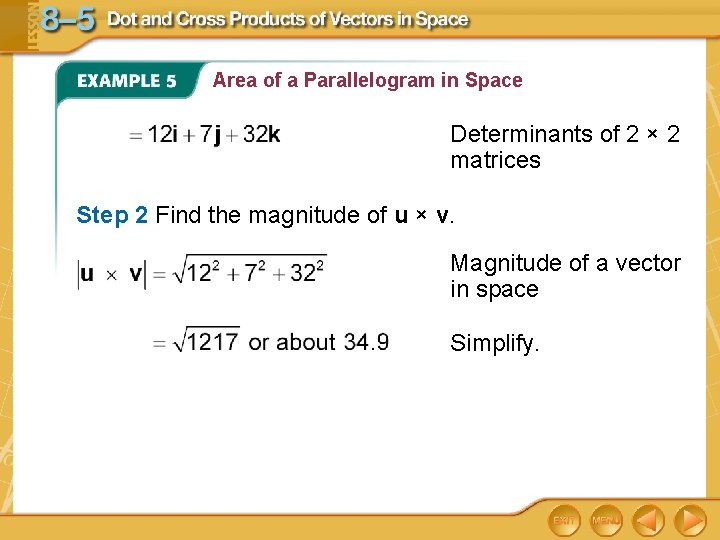
Area of a Parallelogram in Space Determinants of 2 × 2 matrices Step 2 Find the magnitude of u × v. Magnitude of a vector in space Simplify.

Area of a Parallelogram in Space The area of the parallelogram shown is about 34. 9 square units. Answer: or

Find the area of a parallelogram with sides u = 4 i + 5 j – 2 k and v = i – j + 3 k. A. about 7. 3 square units B. about 10. 0 square unit C. about 20. 8 square units D. about 21. 1 square units

Volume of a Parallelepiped Find the volume of the parallelepiped with adjacent edges t = – 3 i + 3 j + 2 k, u = – 3 i – 4 j + 2 k, and v = 5 i – 4 j – k. t = – 3 i + 3 j + 2 k , u = – 3 i – 4 j + 2 k and v = 5 i – 4 j – k Determinant of a 3 × 3 matrix

Volume of a Parallelepiped Determinants of 2 × 2 matrices Simplify. The volume of the parallelepiped shown below is | t ● (u × v)| or 49 cubic units. Answer: 49 cubic units

Find the volume of the parallelepiped with adjacent sides t = 2 i – j + k, u = i + 2 j – k, and v = 2 i + 3 j – k. A. 2 cubic units B. 6 cubic units C. 8 cubic units D. 14 cubic units