Multiplicacin de matrices Manuel Snchez Cuenca Manolo Prez

Multiplicación de matrices Manuel Sánchez Cuenca Manolo Pérez Hernández

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Nociones básicas sobre matrices l Array bidimensional de números l Matriz n x m n filas y m columnas Matriz 3 x 4: 1 3 2 2 2 4 6 3 2 7 4 5

Nociones básicas sobre matrices l Suma de matrices Se suman los elementos de la misma posición en ambas matrices: 1 3 2 3 4 5 5 3 4 1 + 4 1 2 = 7 5 3 1 1 2 2 2 3 4

Nociones básicas sobre matrices l Multiplicación de matrices Sean A (n x l) y B (l x m) dos matrices, entonces cada elemento cij de la matriz resultante se calcula como:

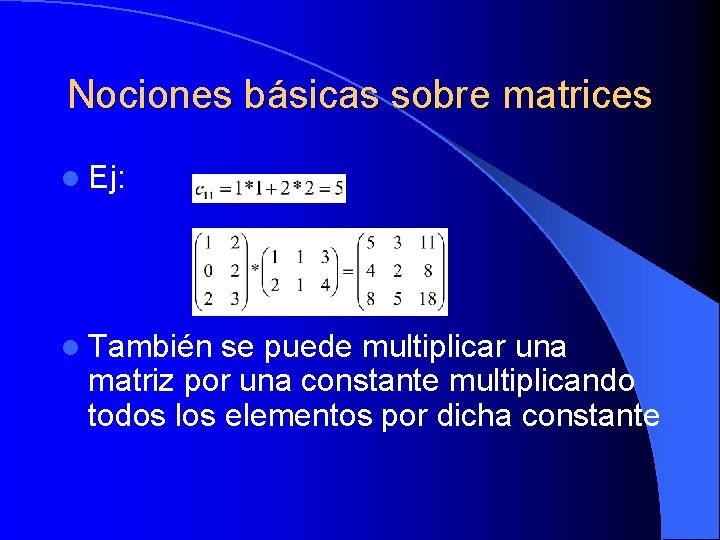
Nociones básicas sobre matrices l Ej: l También se puede multiplicar una matriz por una constante multiplicando todos los elementos por dicha constante

Nociones básicas sobre matrices l Multiplicación de una matriz por un vector Desde el momento que un vector es una matriz con una solo fila o una columna, podemos usar el algoritmo de multiplicación de matrices. Entonces, si el vector B es de la forma n x 1 podemos multiplicarlo por la matriz A (m x n) como A x B; y si el vector A es de la forma 1 x n podemos multiplicarlo por la matriz B (n x m) como A x B.

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Algoritmo secuencial Por simplicidad, todo el tiempo trabajaremos con matrices cuadradas. l for (i = 0; i < n; i++) { for (j = 0; i < n; j++) { c[i][j] = 0; for (k = 0; k < n; k++) { c[i][j] += a[i][k] * b[k][j] } } } l n 3 multiplicaciones y n 3 sumas O (n 3) l

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Algoritmo paralelo l l l Podemos basarnos en el código secuencial, ya que los dos bucles externos son independientes en cada iteración. Con n procesadores podemos obtener O (n 2) Con n 2 procesadores O (n) Estas implementaciones son óptimas en coste, ya que O (n 3) = n x O (n 2) = n 2 x O (n) Estas cálculos no incluyen el coste de las comunicaciones.

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Submatrices Si tenemos muchos menos de n procesadores, cada procesador debe trabajar con un subconjunto de cada una de las matrices submatrices. l Estas submatrices se utilizan como elementos normales, pero teniendo en cuenta que utilizaremos el algoritmo de multiplicación de matrices y de suma de matrices en lugar de la multiplicación y la suma de números implementación recursiva. l

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Implementación directa l Con n 2 procesadores, cada procesador calcula un elemento de C, por lo que necesita una fila de A y una columna de B. l Si usamos submatrices, cada procesador deberá calcular una submatriz de C.

Implementación directa l Análisis de comunicaciones Cada uno de los n 2 procesadores recibe una fila de A y una columna de B, y devuelve un elemento: l Mediante un broadcast de las dos matrices podemos ahorrar tiempo, por ejemplo en un bus tenemos:

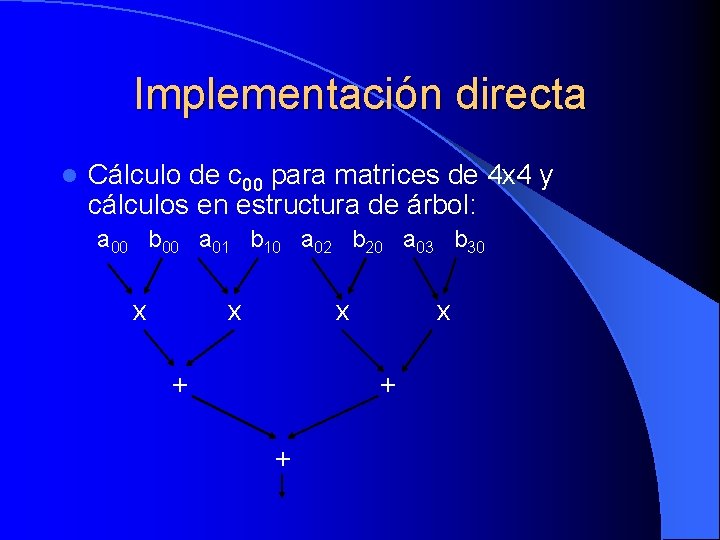
Implementación directa l Análisis de computación Cada procesador realiza n multiplicaciones y n sumas, por lo que tenemos: l Usando una estructura de árbol y n 3 procesadores podemos obtener un tiempo de computación de O (log n)

Implementación directa l Cálculo de c 00 para matrices de 4 x 4 y cálculos en estructura de árbol: a 00 b 00 a 01 b 10 a 02 b 20 a 03 b 30 x x x + +

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Implementación con submatrices l En cualquiera de los métodos se pueden sustituir los elementos de la matriz por submatrices para reducir el número de procesadores l Con submatrices de m x m y s = n/m es como si tuviésemos matrices de s x s con submatrices de m x m en lugar de elementos simples.

Implementación con submatrices l Análisis de comunicaciones Cada uno de los s 2 procesadores recibe una fila de submatrices de A y una columna de submatrices de B, y devuelve una submatriz:

Implementación con submatrices Al aumentar el tamaño de las submatrices (y disminuir el número de procesadores) el tiempo de transmitir un mensaje aumenta pero el número de mensajes disminuye, por lo que es posible encontrar un valor óptimo del tamaño de la submatriz. Además, también es posible hacer un broadcast de las dos matrices completas.

Implementación con submatrices l Análisis de computación Cada procesador realiza s multiplicaciones y s sumas de submatrices, una multiplicación de submatrices necesita m 3 multiplicaciones y m 3 sumas y una suma m 2 sumas, por lo que en resumen, el tiempo de computación es:

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Implementación recursiva La división en submatrices sugiere una estrategia recursiva de divide y vencerás, que puede ser especialmente ventajoso en sistemas de memoria compartida. l El proceso de dividir una matriz en submatrices para repartir el trabajo entre otros procesadores debe parar cuando ya no queden procesadores libres. l La ventaja de esta estrategia es que en cada paso de recursión, los datos transmitidos son más pequeños y están más localizados. l

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Algoritmo de Cannon l Este algoritmo y el siguiente son especialmente apropiados para sistemas de paso de mensajes, y la arquitectura de paso de mensajes que más se ajusta a las matrices es una malla. Realmente, aunque la arquitectura física no sea una malla, lógicamente cualquier arquitectura puede representarse como una malla.

Algoritmo de Cannon l Utiliza una malla conexiones entre los elementos de cada lado (toro) para desplazar los elementos de A hacia la izquierda y los de B hacia arriba. l El algoritmo sigue los siguientes pasos: 1. El procesador Pij tiene los elementos aij y bij.

Algoritmo de Cannon 2. La fila i-ésima de A se desplaza i posiciones a la izquierda, y la columna j -ésima de B se desplaza j posiciones hacia arriba, y todo esto teniendo en cuenta que el elemento que sale por un extremo entra por el otro. Con este paso se consigue que el procesador Pij contenga los elementos aij+i y bi+jj, que son necesarios para calcular cij.

Algoritmo de Cannon 3. Cada procesador multiplica su par de elementos. 4. Cada fila de A se desplaza una posición a la izquierda, y cada columna de B una posición hacia arriba. 5. Cada procesador multiplica su nuevo par de elementos, y suma el resultado al anterior. 6. Se repiten los pasos 4 y 5 hasta terminar, es decir n – 1 desplazanientos

Algoritmo de Cannon Ej:

Algoritmo de Cannon

Algoritmo de Cannon

Algoritmo de Cannon l Análisis de comunicaciones Los desplazamientos iniciales requieren un máximo de n-1 desplazamientos, y después se realizarán n-1 desplazamientos (uno en cada paso) por lo que tenemos el siguiente tiempo de comunicaciones: Esto nos da O (n)

Algoritmo de Cannon En el caso de que estemos trabajando con submatrices, tenemos s-1 desplazamientos iniciales como máximo, y s-1 desplazamientos después, cada uno de ellos de m 2 elementos: Lo que nos da O (sm 2) = O (nm)

Algoritmo de Cannon l Análisis de computación Cada procesador realiza n multiplicaciones y n-1 sumas para calcular su elemento de C, lo que implica O (n). Usando submatrices, cada procesador realiza m 3 multiplicaciones y m 3 sumas por cada multiplicación, y m 2 sumas por cada suma, y realiza s multiplicaciones y s-1 sumas: Lo que da O (sm 3) = O (nm 2)

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

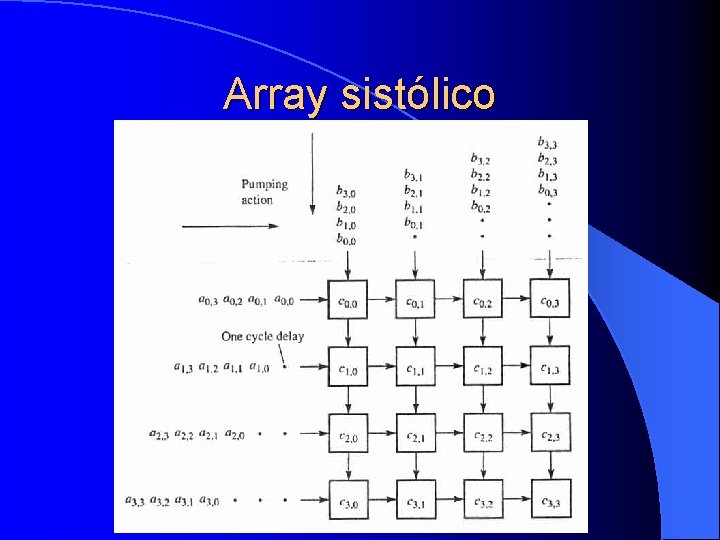
Array sistólico La información es bombeada al array sistólico en varias direcciones a intervalos regulares. l Concretamente, la información es bombeada desde la izquierda hacia la derecha y desde arriba hacia abajo. l Los datos se encuentran en los nodos, y entonces se multiplican y suman al valor calculado anteriormente. l

Array sistólico

Array sistólico Ej:

Array sistólico

Array sistólico

Array sistólico

Array sistólico l Análisis de comunicaciones Se realizan n desplazamientos para que la última fila y ultima columna entren, n– 1 para que entre el último elemento y n-1 para que llegue al final, por lo que tenemos el siguiente tiempo de comunicaciones: Esto nos da O (n)

Array sistólico l Análisis de computación Cada procesador realiza n multiplicaciones y n-1 sumas, lo que nos da un orden de complejidad O (n)

Array sistólico l Multiplicación de una matriz por un vector: Esta técnica puede utilizarse directamente para multiplicar una matriz por un vector usando simplemente un array de 1 xn o de nx 1, según sea el vector.

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Algoritmo de Fox Matrices de tamaño n x n l Se particionan a través de p procesadores. l l Hace uso de un broadcast de uno a muchos de los bloques de la matriz A en filas de procesadores, y de un paso de bloques de la matriz B a través de las columnas de los procesadores en forma ascendente de procesador en procesador. l Inicialmente se selecciona cada bloque Ai, j de la diagonal para un broadcast.

Algoritmo de Fox Repetir 1. 2. 3. 4. veces Broadcast del bloque seleccionado de A a través de los procesadores de la fila en que está ubicado el bloque. Multiplicar el bloque recibido de A como resultado del broadcast por el bloque residente de B (el procesador que inicia el broadcast ya tiene el bloque requerido de A). Enviar el bloque de B al procesador directamente precedente en la columna del procesador (con enrollamiento), y recibir un bloque de refresco de B desde el procesador posterior. Seleccionar el bloque de A para el broadcast de la siguiente fila. Si se ha realizado un broadcast de Ai, j en la etapa actual, entonces seleccionar para el próximo broadcast A [i, (j+1)mod ].

Algoritmo de Fox l Pasos de Comunicación con 16 procesadores

Algoritmo de Fox l Tiempo de ejecución paralelo sobre un Hipercubo – Cada procesador gasta un tiempo de n 3/p en la computación. – El tiempo para el broadcast de uno a todos los bloques de A domina sobre el tiempo para el cambio en pasos simples de los bloques de B.

Algoritmo de Fox – Si la malla original de procesadores encaja en un hipercubo, cada broadcast puede ser ejecutado en un tiempo – Como esta operación se repite veces, el tiempo total de comunicación es

Algoritmo de Fox – Y el tiempo de ejecución paralelo Aunque el tiempo de ejecución paralelo y la escalabilidad de este algoritmo son inferiores a los de los algoritmos simple y de Cannon, el tiempo de ejecución de este algoritmo puede ser mejorado intercalando computación y comunicación por pipelines.

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Algoritmo DNS l Debe su nombre a Dekel, Nassimi y Sahni. l Algoritmo paralelo que puede consumir n 3 procesadores y ejecuta la multiplicación de matrices en un tiempo Θ(log n) usando Ω(n 3/log n) procesadores.

Algoritmo DNS l Algoritmo CREW PRAM sin concentrarse en una red de interconexión particular. – n 3 procesadores. – Dos matrices n x n. – Procesadores colocados en un array lógico tridimensional n x n. – A cada procesador se le asigna una multiplicación escalar. – Los procesadores se etiquetan de acuerdo a su posición en el array. – La multiplicación A[i, k] x B[k, j] se asigna a Pi, j, k.

Algoritmo DNS – Después de que cada procesador ejecute una multiplicación simple se suman los contenidos de Pi, j, 0, Pi, j, 1, …, Pi, j, n-1 para obtener C[i, j]. – La suma de todos los C[i, j] se puede llevar a cabo simultáneamente a lo largo de los n pasos.

Algoritmo DNS l Tiempo de ejecución – Toma un paso para multiplicar y los n pasos para sumar, por tanto, emplea un tiempo Θ(log n)

Algoritmo DNS l Algoritmo paralelo usando un Hipercubo – El array lógico tridimensional se mapea en un hipercubo con n 3 = w 3 d procesadores. – Los procesadores se pueden visualizar como n planos de n x n procesadores cada uno. – Cada plano corresponde a un valor diferente de k. – Inicialmente, las matrices se distribuyen a lo largo de los n 2 procesadores del plano correspondiente a k=0 en la base del array tridimensional de procesadores. – Inicialmente, el procesador Pi, j, 0 almacena A[i, j] y B[i, j].

Algoritmo DNS 1. Cada columna de A se mueve a diferentes planos, de tal forma que la columna j ocupa la misma posición en el plano correspondiente a k = j (igual que se hizo inicialmente con k = 0) 2. Todas las columnas de A se replican n veces en sus respectivos planos por medio de un broadcast a lo largo del eje j. Como resultado, cada uno de los n procesadores, Pi, 0, j, Pi, 1, j, …, Pi, n-1, j recibe una copia de A[i, j] desde Pi, j, j.

Algoritmo DNS – Después de esto, cada columna vertical de procesadores Pi, j, * tiene la fila A[i, *]. En concreto, el procesador Pi, j, k tiene A[i, k]. – Para la matriz B, los pasos de comunicación son similares, pero las reglas de i y j en los procesadores descritos se permutan.

Algoritmo DNS – Después de estos pasos de comunicación, se multiplican A[i, k] y B[k, j] en Pi, j, k. – Cada elemento C[i, j] de la matriz producto se obtiene por acumulación de nodos simples a través del eje k. – Durante este paso, el procesador Pi, j, 0 acumula el resultado de las multiplicaciones de los procesadores Pi, j, 1, Pi, j, 2, …, Pi, j, n-1.

Algoritmo DNS l Pasos de comunicación principales 1. Mover las columnas de A y las filas de B a sus respectivos planos. 2. Ejecutar un broadcast a lo largo del eje j para A y a lo largo del eje i para B. 3. Acumular los nodos simples a lo largo del eje k. Todas estas operaciones se ejecutan en subcubos del hipercubo de n procesadores.

Algoritmo DNS l Patrón de comunicación para distribuir los elementos de A a lo largo de los procesadores.

Algoritmo DNS

Algoritmo DNS l Tiempo de ejecución – El tiempo de ejecución paralelo usando el algoritmo DNS sobre un Hipercubo con n 3 procesadores es de Θ(log n).

Algoritmo DNS l CREW PRAM Vs. Hipercubo – En CREW PRAM la columna vertical de procesadores, Pi, j, *, computa el producto puntual de la fila A[i, *] y la columna B[*, j]. – No se necesita ningún paso de movimiento de datos porque en CREW PRAM cada procesador puede acceder a cualquier localización en tiempo constante.

Algoritmo DNS l CREW PRAM Vs. Hipercubo – En un Hipercubo, las filas de A y las columnas de B deben ser movidas apropiadamente para que cada columna vertical del procesador Pi, j, * tenga la fila A[i, *] y la columna B[*, j]. – El procesador Pi, j, k debería tener A[i, k] y B[k, j].

Algoritmo DNS l Algoritmo DNS con menos de n 3 procesadores – El algoritmo DNS no es de coste optimo para n 3 procesadores, su tiempo de procesador es Θ(n 3 log n) que excede de la complejidad secuencial, Θ(n 3).

Algoritmo DNS – Número de procesadores p = q 3 para algún q < n. – Las dos matrices se particionan en bloques de tamaño (n/q) x (n/q). Es decir, cada matriz se considera un array cuadrado de bloques de tamaño q x q. – La diferencia es que ahora operamos sobre bloques en vez de sobre elementos individuales. – Como 1 ≤ q ≤ n, el número de procesadores puede variar entre 1 y n 3.

Algoritmo DNS l Tiempo de ejecución en un Hipercubo con enrutamiento de corte completo – El primer paso de comunicación uno a uno se ejecuta en A y en B y toma un tiempo para cada matriz de ts + tw (n/q)2 + th log q. – El segundo paso es un broadcast de uno a todos que se ejecuta en A y en B y toma un tiempo para cada matriz de ts log q + tw (n/q)2 log q.

Algoritmo DNS – La acumulación de nodo simple final se ejecuta una sola vez (para la matriz C) y toma un tiempo ts + log q + tw (n/q)2 log q.

Algoritmo DNS – Asumiendo que cada par multiplicación-suma toma unidad de tiempo, la multiplicación de submatrices de tamaño (n/q) x (n/q) toma un tiempo de (n/q)3. – Se puede ignorar el tiempo de comunicación para el primer paso de comunicación uno a uno y el tiempo de computación para la suma en la fase de acumulación final.

Algoritmo DNS Las expresiones aproximadas para el tiempo de ejecución paralelo es El sistema paralelo es de coste óptimo para n 3 = Ω(p log p) ó para p = Ο(n 3 / log n)

Algoritmo DNS l Tiempo de ejecución sobre una malla 3 D con enrutamiento de corte completo – El algoritmo DNS no es adecuado para una malla bidimensional, ya que el algoritmo mapea naturalmente sobre una malla tridimensional de procesadores y una malla tridimensional no se puede ajustar a una malla bidimensional sin congestión ni dilatación excesivas.

Algoritmo DNS – Sobre una malla tridimensional, el algoritmo de hipercubo se modificaciones. puede implementar sin – Solo hay un cambio en la ecuación de la expresión del tiempo de ejecución paralelo, que es la suma del termino 3*th*p 1/3. – Es decir, el tiempo de ejecución paralelo es

Multiplicación de matrices l l l Nociones básicas sobre matrices Algoritmo secuencial Algoritmo paralelo Submatrices Implementación directa Implementación con submatrices Implementación recursiva Algoritmo de Cannon Array sistólico Algoritmo de Fox Algoritmo DNS Mapeo de matrices en procesadores

Mapeo de matrices en procesadores l Particionamiento rayado l Particionamiento de tablero de damas

Mapeo de matrices en procesadores l Particionamiento rayado l Particionamiento de tablero de damas

Particionamiento rayado l Se divide la matriz en grupos de filas o columnas completas y a cada procesador se le asigna un grupo. l Se llama uniforme si cada grupo contiene el mismo número de filas o columnas. l Se llama rayado de bloque si a cada procesador se le asignan filas o columnas contiguas.

Particionamiento rayado l Se llama rayado cíclico si las filas o columnas se distribuyen secuencialmente a través de los procesadores de forma cíclica. l Se llama rayado cíclico de bloque si la matriz se divide en bloques de q filas (q < n/p) y los bloques se distribuyen en los procesadores de forma cíclica.

Mapeo de matrices en procesadores l Particionamiento rayado l Particionamiento de tablero de damas

Particionamiento de tablero de damas l La matriz se divide en bloques o submatrices cuadradas o rectangulares más pequeñas y se distribuyen a través de los procesadores. l Divide las filas y columnas de la matriz para que a ningún procesador se le asigne una fila o columna completa.

Particionamiento de tablero de damas l Se llama particionamiento de tablero de damas uniforme si todas las submatrices son de igual tamaño. l Puede ser de bloque, cíclico o cíclico de bloque. l En el particionamiento cíclico mapeamos las filas en los procesadores de forma cíclica y después las columnas o viceversa.

Particionamiento de tablero de damas l En el particionamiento cíclico de bloque dividimos la matriz en q 2 p bloques y mapeamos esos bloques de tamaño q x q de forma cíclica. l Una matriz cuadrada paticionada por tablero de damas se mapea naturalmente en una malla bidimensional de procesadores.

Particionamiento rayado Vs. de tablero de damas l El nivel más bajo de granularidad en el de tablero de damas es un elemento de matriz por procesador. l El de tablero de damas puede explotar más la concurrencia (siempre que el algoritmo paralelo lo permita) porque la computación se puede dividir en más procesadores que el de rayado.