Cordinaten Transformaties Matrices Een matrix is een rechthoekige

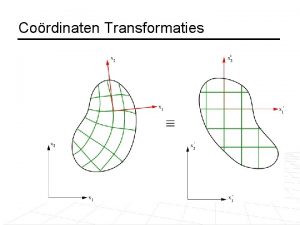
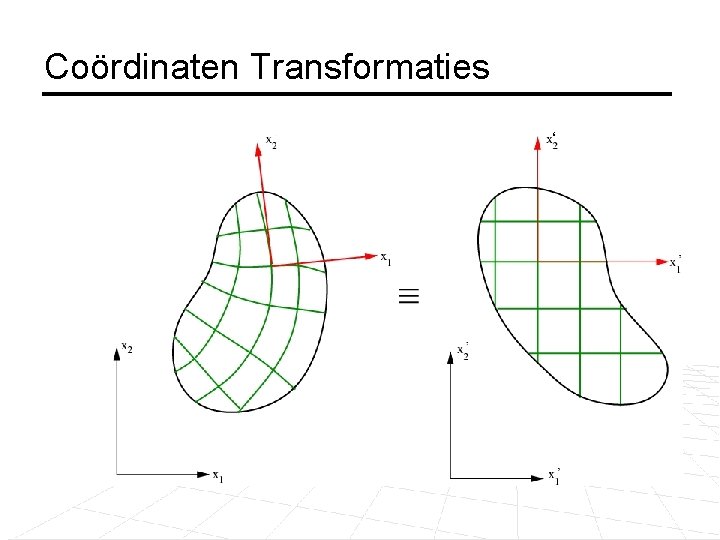
Coördinaten Transformaties ‘

Matrices • Een matrix is een rechthoekige set getallen • We stellen de matrix voor met een hoofdletter A in dit geval • Het element op de i-de rij en j-de kolom geven we aan met aij. Merk op dat de index in dit geval begint bij 1 (dat is gebruikelijk voor de indices i, j en k. Voor en b gaat de index over 0, 1, 2 en 3.

Matrices – Optellen • Gegeven twee matrices A en B als we B optellen bij A (dat is de vorm A+B) dan als A is (n m), moet B ook (n m), anders is A+B is niet gedefinieerd • De optelling produceert het resultaat , C = A+B, met elementen:

Matrices – Vermenigvuldigen • Gegeven twee matrices A en B als we B vermenigvuldigen met A (dat is de vorm AB) dan als A (n m) is, moet B (m p) zijn, d. w. z. het aantal kolommen van A moet gelijk zijn aan het aantal rijen van B. Anders is AB niet gedefinieerd. • De vermenigvuldiging produceert het resultaat C = AB, met elementen: (In feite vermenigvuldigen we de eerste rij van A met de eerste kolom van B en stoppen het resultaat in element c 11 van C. Enzovoort. . . ).

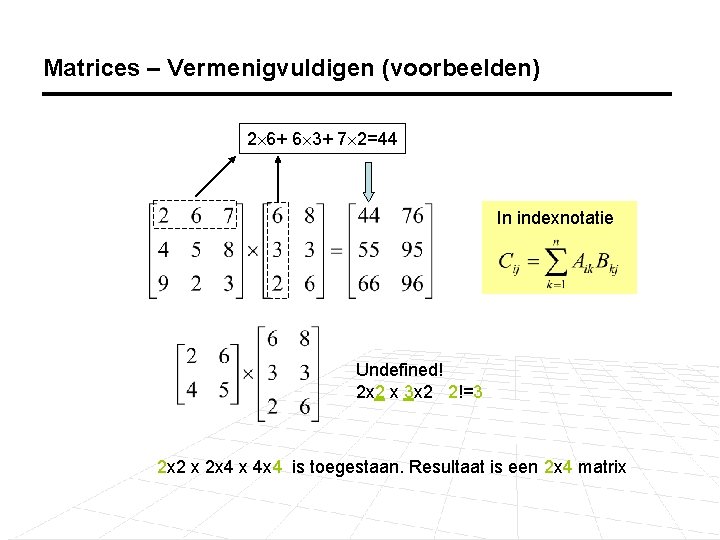
Matrices – Vermenigvuldigen (voorbeelden) 2 6+ 6 3+ 7 2=44 In indexnotatie Undefined! 2 x 2 x 3 x 2 2!=3 2 x 2 x 2 x 4 x 4 x 4 is toegestaan. Resultaat is een 2 x 4 matrix

Matrices – Opmerkingen • Er geldt AB ≠ BA • Matrix vermenigvuldiging is additief: A(B+C) = AB + AC • Eenheidsmatrix voor vermenigvuldiging is I. • De getransponeerde van een matrix A wordt aangegeven met AT en wordt verkrijgen door omwisselen van rijen en kolommen van A:

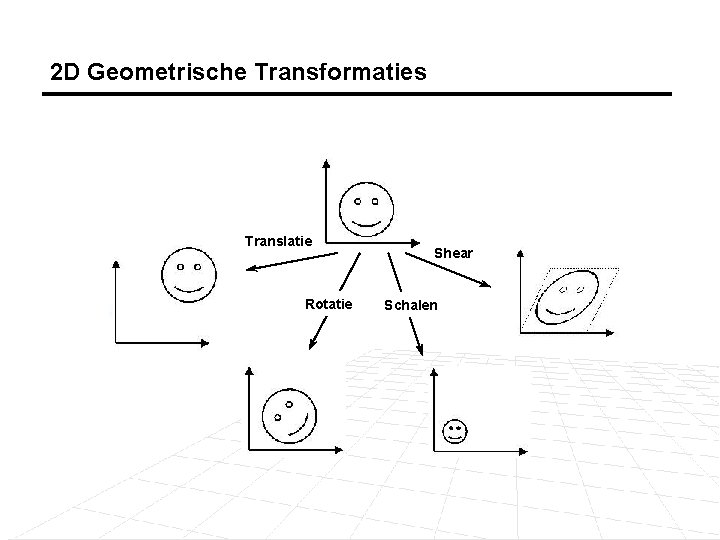
2 D Geometrische Transformaties Translatie Rotatie Shear Schalen

Translatie van vectoren Stel we hebben vector en willen een translatie uitvoeren met vector. De nieuwe vector wordt gevonden uit de som In matrixvorm:

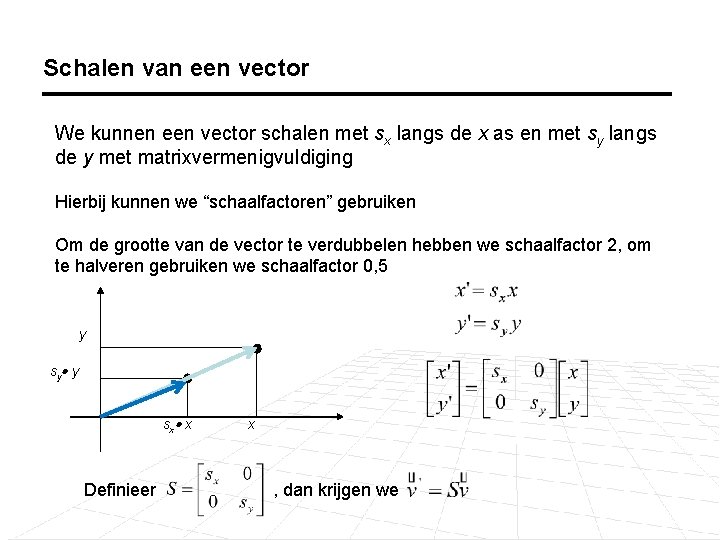
Schalen van een vector We kunnen een vector schalen met sx langs de x as en met sy langs de y met matrixvermenigvuldiging Hierbij kunnen we “schaalfactoren” gebruiken Om de grootte van de vector te verdubbelen hebben we schaalfactor 2, om te halveren gebruiken we schaalfactor 0, 5 y sy y sx x Definieer x , dan krijgen we

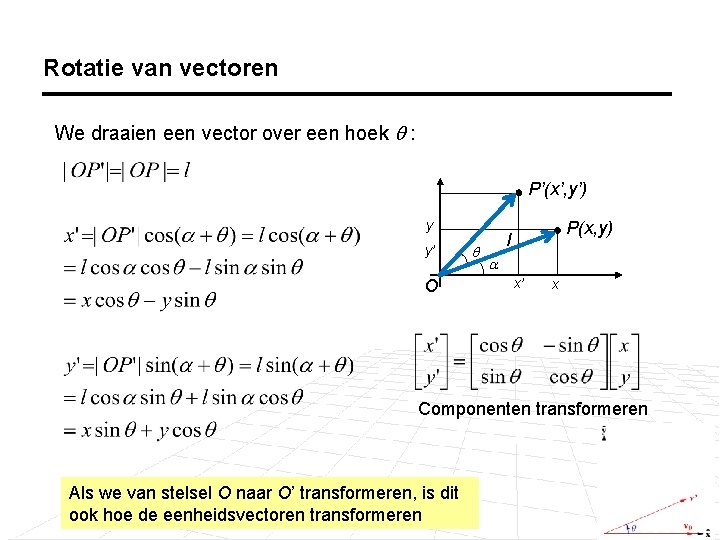
Rotatie van vectoren We draaien een vector over een hoek : P’(x’, y’) y y’ O P(x, y) l x’ x Componenten transformeren Als we van stelsel O naar O’ transformeren, is dit ook hoe de eenheidsvectoren transformeren

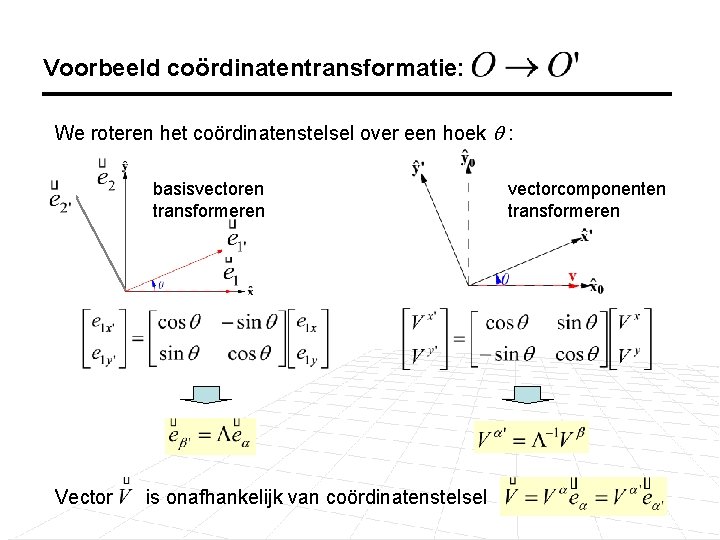
Voorbeeld coördinatentransformatie: We roteren het coördinatenstelsel over een hoek : basisvectoren transformeren Vector is onafhankelijk van coördinatenstelsel vectorcomponenten transformeren

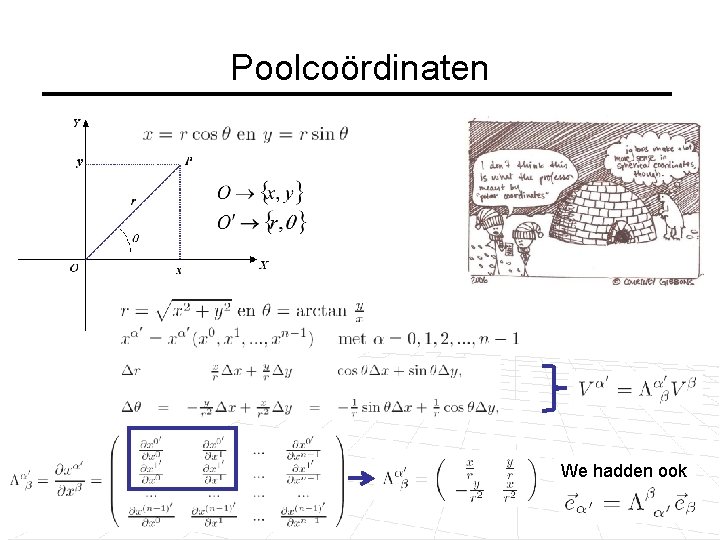
Poolcoördinaten We hadden ook

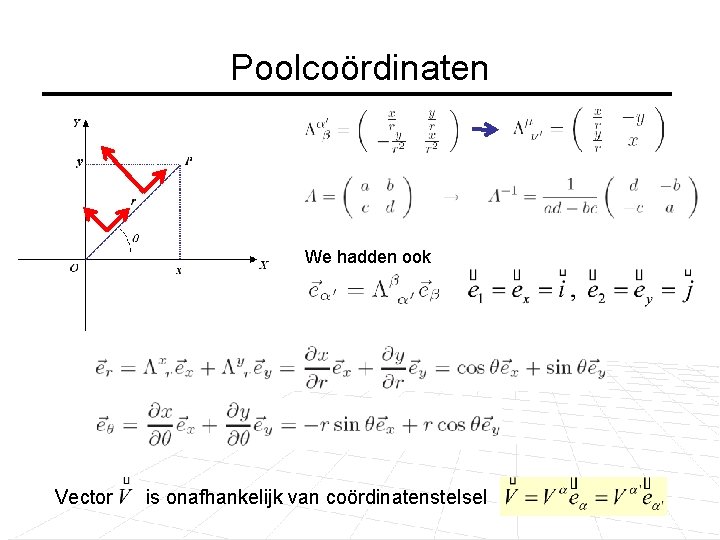
Poolcoördinaten We hadden ook Vector is onafhankelijk van coördinatenstelsel