Mechanika Kwantowa IV Atom wodoru WYKAD 9 Atom

Mechanika Kwantowa IV. Atom wodoru WYKŁAD 9 Atom wodoru – podstawy

Plan wykładu • • • operator orbitalnego momentu pędu we współrzędnych kartezjańskich i sferycznych, operator kwadratu orbitalnego momentu pędu we współrzędnych sferycznych, harmoniki sferyczne, Hamiltonian cząstki w polu centralnym, radialne równanie Schrödingera, liczby kwantowe.

Podstawowe informacje Podstawowe dane dla atomu wodoru • masa protonu: • masa elektronu: • masa zredukowana elektronu: • energia jonizacji atomu wodoru:

Podstawowe informacje Podstawowe dane dla atomu wodoru • promień protonu: • promień najniższej „orbity” elektronowej:

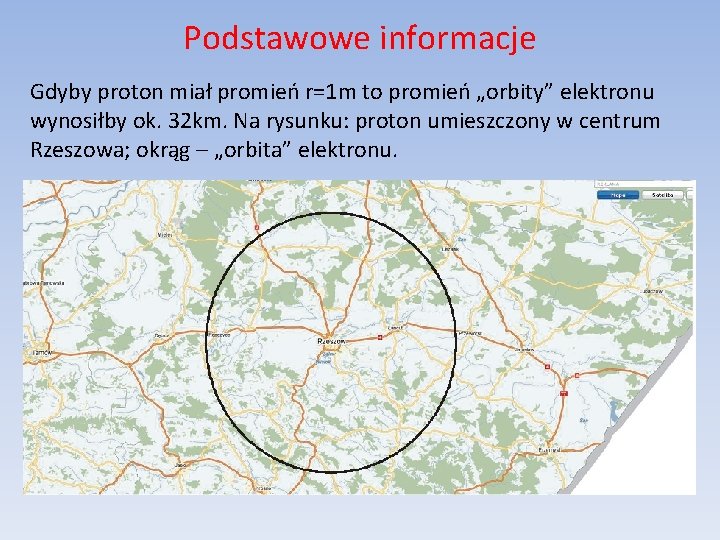
Podstawowe informacje Gdyby proton miał promień r=1 m to promień „orbity” elektronu wynosiłby ok. 32 km. Na rysunku: proton umieszczony w centrum Rzeszowa; okrąg – „orbita” elektronu.

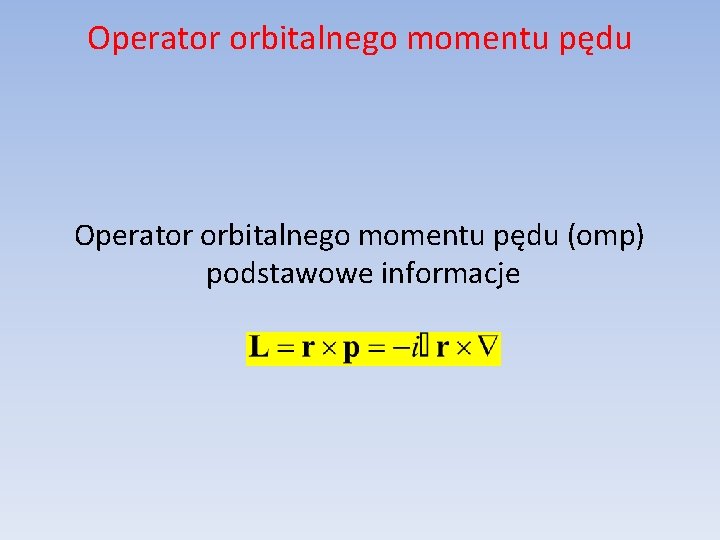
Operator orbitalnego momentu pędu (omp) podstawowe informacje

Operator omp we współrzędnych kartezjańskich Składowe operatora omp (L) w reprezentacji położeniowej (współrzędne kartezjańskie):

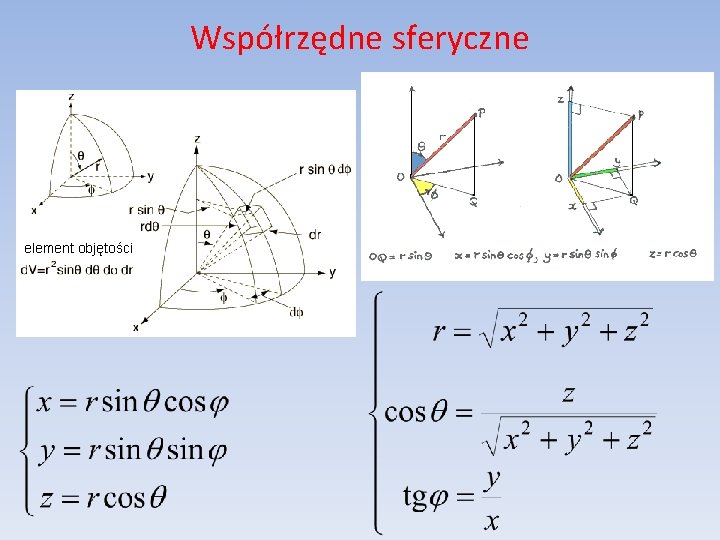
Współrzędne sferyczne element objętości

Operator omp we współrzędnych sferycznych* Operatory Li we współrzędnych sferycznych:

Operator orbitalnego momentu pędu Wprowadzamy operator całkowitego momentu pędu zdefiniowany jako: przy czym:

Operator omp we współrzędnych sferycznych* Operator L 2 we współrzędnych sferycznych:

Hamiltonian cząstki w polu centralnym Zakładamy, że cząstka o masie porusza się w pewnym polu, którego centrum umieszczone jest w początku układu współrzędnych. Energia potencjalna cząstki dana jest funkcją V=V(r) i zależy jedynie od odległości cząstki od centrum pola. Mówimy wtedy, że cząstka porusza się w polu o potencjale centralnym.

Hamiltonian cząstki w polu centralnym Hamiltonian cząstki poruszającej się w polu centralnym ma postać gdzie Postać hamiltonianu zależy od postaci członu opisującego energię potencjalną.

Hamiltonian cząstki w polu centralnym Stacjonarne równanie Schrödingera ma postać: W rozpatrywanym przez nas przypadku potencjał ma z założenia symetrię sferyczną, tak więc bardziej użytecznym będzie posługiwanie się układem współrzędnych sferycznych.

Hamiltonian cząstki w polu centralnym Musimy więc rozwiązać stacjonarne równanie Schrödingera we współrzędnych sferycznych w postaci

Separacja zmiennych Ponieważ składowe operatora momentu pędu działają jedynie na zmienne kątowe, więc komutują one ze wszystkimi operatorami działającymi na zmienną radialną. Mamy więc: Tak więc jako zupełny zbiór komutujących obserwabli wybieramy H, L 2 oraz L 3, dla których to operatorów mamy wspólne stany własne.

Separacja zmiennych Możemy napisać: Pamiętamy także, że: gdzie Y to tzw. harmoniki sferyczne.

Zagadnienie własne omp Żądanie, aby liczba kwantowa m była liczbą całkowitą wynika z żądania niezmienniczości układu fizycznego przy obrotach o kąt 2. Z faktu, że m jest liczbą całkowitą wynika, że liczba kwantowa l też musi być liczbą całkowitą, ponieważ zmienia się ona od –l do l co jeden.

Harmoniki sferyczne Kilka przykładów

Harmoniki sferyczne Kilka przykładów

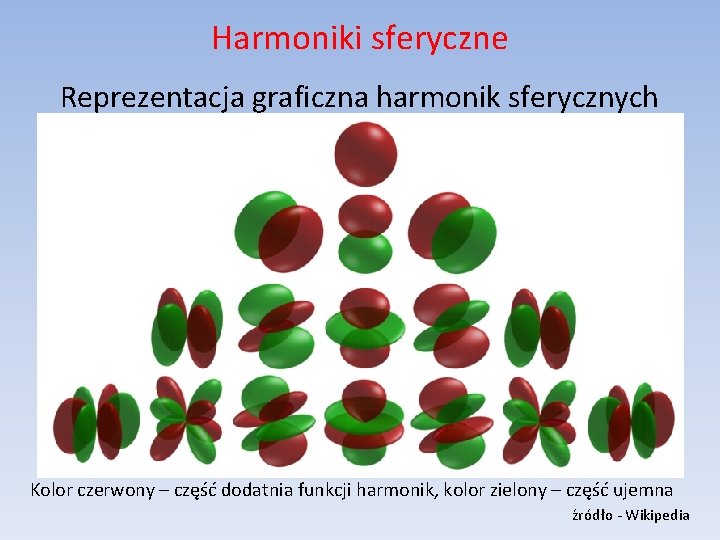
Harmoniki sferyczne Reprezentacja graficzna harmonik sferycznych Kolor czerwony – część dodatnia funkcji harmonik, kolor zielony – część ujemna źródło - Wikipedia

Radialne równanie Schrödingera Wykorzystując postać funkcji falowej: w równaniu otrzymamy radialne równanie Schrödingera:

Radialne równanie Schrödingera Ponieważ w równaniu radialnym występuje liczba kwantowa l oraz wiemy, że dla każdego l mamy 2 l+1 możliwych wartości liczby kwantowej m, tak więc funkcja radialna R(r) będzie zależeć od dwóch parametrów:

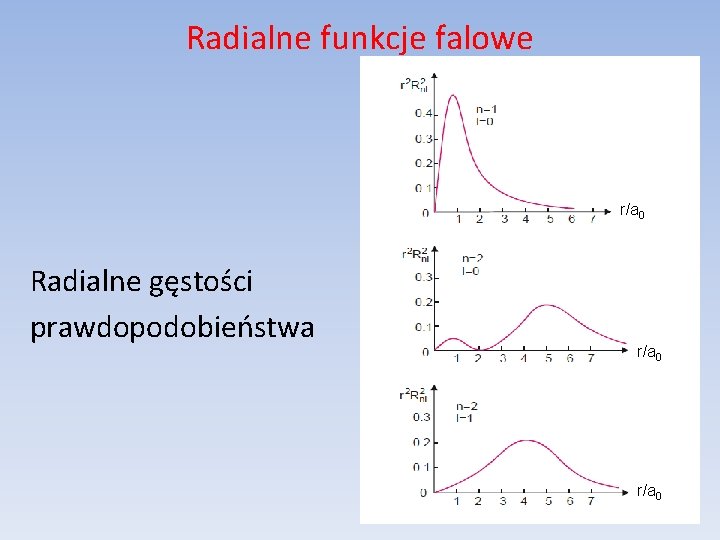
Radialne funkcje falowe r/a 0 Radialne gęstości prawdopodobieństwa r/a 0

Liczby kwantowe Podsumowanie 1) Dla cząstki poruszającej się w potencjale centralnym funkcje falowe zależą co najmniej od trzech liczb kwantowych Funkcje te są funkcjami własnymi operatora Hamiltona, kwadratu momentu pędu oraz rzutu momentu pędu na oś z.

Liczby kwantowe 2) Funkcje własnym: odpowiadają wartościom - energia - pełny moment pędu - rzut momentu pędu na oś z Nazewnictwo liczb kwantowych: n – główna (radialna) liczba kwantowa; l – orbitalna liczba kwantowa; m – magnetyczna liczba kwantowa.

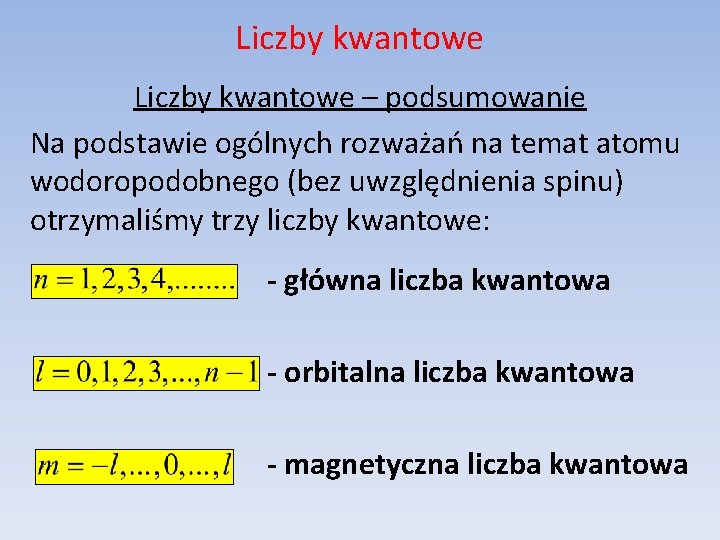
Liczby kwantowe – podsumowanie Na podstawie ogólnych rozważań na temat atomu wodoropodobnego (bez uwzględnienia spinu) otrzymaliśmy trzy liczby kwantowe: - główna liczba kwantowa - orbitalna liczba kwantowa - magnetyczna liczba kwantowa

Liczby kwantowe Stany charakteryzowane określoną liczbą n nazywamy powłoką elektronową. Liczba orbitalna l określa podpowłoki. Notacja spektroskopowa:

Liczby kwantowe Przykład:

Radialne funkcje falowe Wizualizacja orbitali atomu wodoru: http: //www. falstad. com/qmatom/index. html