Mechanika Kwantowa III Proste zagadnienia kwantowe WYKAD 9

Mechanika Kwantowa III. Proste zagadnienia kwantowe WYKŁAD 9 Oscylator harmoniczny

Plan wykładu • • hamiltonian oscylatora harmonicznego, rozwiązanie przy pomocy wielomianów Hermite’a, rozwiązanie przy pomocy operatorów kreacji i anihilacji, hamiltonian w bazie energii.

Hamiltonian oscylatora harmonicznego Rozważmy potencjał (energię potencjalną) 1 -wymiarowego oscylatora harmonicznego Wiele potencjałów posiadających minimum w pobliżu punktu x 0 można przybliżyć wokół tego punktu potencjałem typu oscylatora harmonicznego.

Rozwinięcie potencjału Szereg Taylora:

Klasyczny oscylator harmoniczny - rozwiązanie ogólne; gdzie ; - wahadło matematyczne:

Hamiltonian oscylatora harmonicznego Hamiltonian dla oscylatora ma postać: gdzie . Odpowiednie równanie Schrödingera ma postać:

Hamiltonian oscylatora harmonicznego Dokonując zamiany zmiennych (na bezwymiarowe) otrzymamy ostatecznie: Wielkość jest „naturalną” jednostką długości dla omawianego zagadnienia. Sformułowanie nabiera

Hamiltonian oscylatora harmonicznego Zachowanie asymptotyczne ( Rozwiązanie ścisłe: gdzie funkcja f spełnia równanie: ):

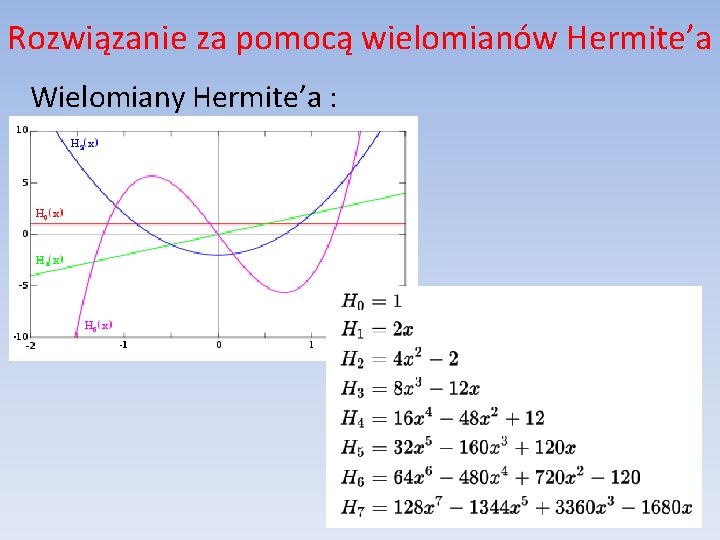
Rozwiązanie za pomocą wielomianów Hermite’a Wielomiany Hermite’a spełniają równanie: Podstawowe własności:

Rozwiązanie za pomocą wielomianów Hermite’a Wielomiany Hermite’a :

Rozwiązanie za pomocą wielomianów Hermite’a Powtórzenie: - równanie oscylatora: - równanie Hermite’a: czyli:

Rozwiązanie za pomocą wielomianów Hermite’a Tak więc funkcje falowe i energie mają postać: gdzie:

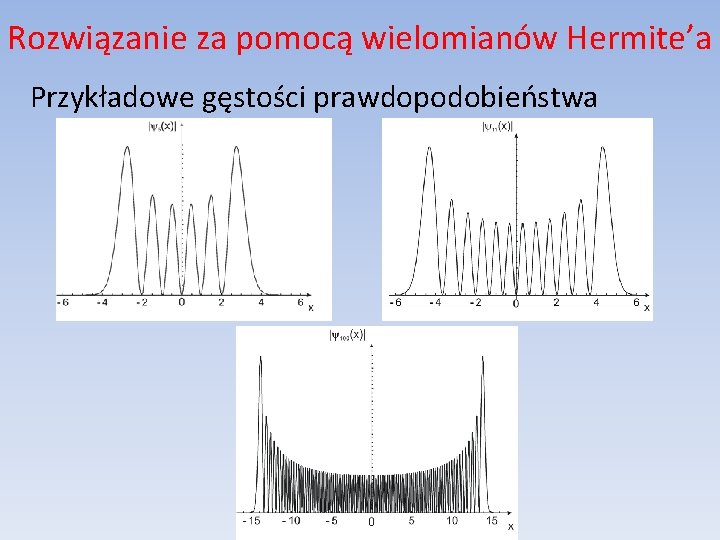
Rozwiązanie za pomocą wielomianów Hermite’a Przykładowe gęstości prawdopodobieństwa

Rozwiązanie za pomocą wielomianów Hermite’a Można wykazać, że:

Rozw. za pomocą operatorów kreacji i anihilacji Hamiltonian dla oscylatora harmonicznego zapiszemy używając operatorów anihilacji i kreacji

Rozw. za pomocą operatorów kreacji i anihilacji Podstawowe własności operatorów kreacji i anihilacji:

Rozw. za pomocą operatorów kreacji i anihilacji Operatory położenia i pędu mają postać:

Rozw. za pomocą operatorów kreacji i anihilacji Hamiltonian przyjmie postać: Funkcje falowe otrzymujemy ze stanów: gdzie stan próżni obliczamy z warunku: otrzymując wynik identyczny jak poprzednio (przy zastosowaniu metody wielomianów Hermite’a).

Rozw. za pomocą operatorów kreacji i anihilacji Elementy macierzowe:

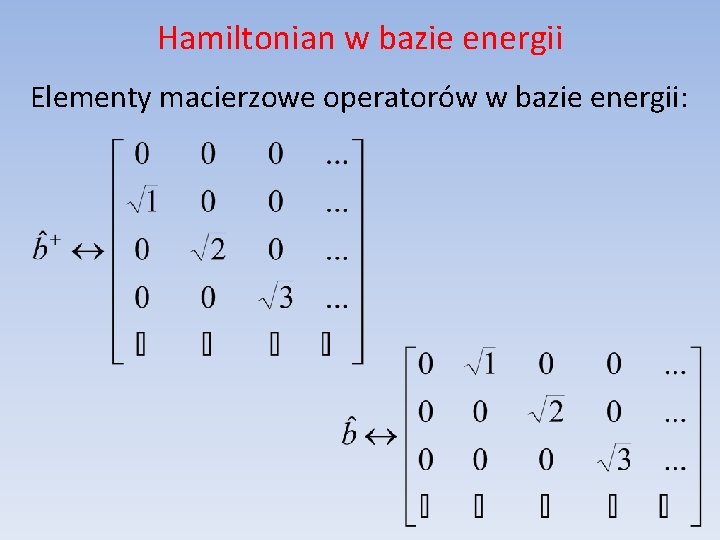
Hamiltonian w bazie energii Elementy macierzowe operatorów w bazie energii:

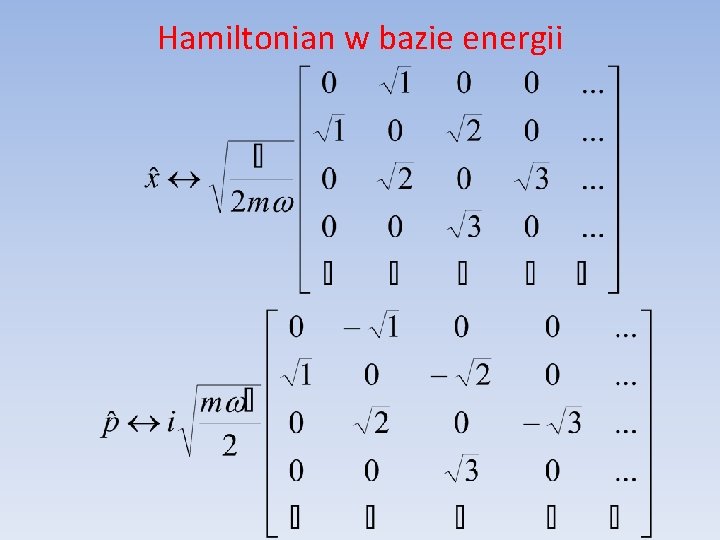
Hamiltonian w bazie energii

Hamiltonian w bazie energii: