Least Square Method Line fitting Hyperplane fitting Function
![Form X and b X=[x' ones(n, 1)]; b=y'; Adavanced Numerical Computation 2008, AM NDHU](https://slidetodoc.com/presentation_image_h2/9d627d1183f1704b917d565122cd10d7/image-6.jpg "Form X and b X=[x' ones(n, 1)]; b=y'; Adavanced Numerical Computation 2008, AM NDHU")
![>> >> n=30; X=rand(n, 2); b=rand(n, 1); X=[X ones(n, 1)]; a=pinv(X)*b; aa=inv(X'*X)*(X'*b); sum(abs(a-aa)) ans](https://slidetodoc.com/presentation_image_h2/9d627d1183f1704b917d565122cd10d7/image-32.jpg ">> >> n=30; X=rand(n, 2); b=rand(n, 1); X=[X ones(n, 1)]; a=pinv(X)*b; aa=inv(X'*X)*(X'*b); sum(abs(a-aa)) ans")
![Linear assumption Predictor x=[x 1, …, x 13]T l y = a 1*x 1+a](https://slidetodoc.com/presentation_image_h2/9d627d1183f1704b917d565122cd10d7/image-48.jpg "Linear assumption Predictor x=[x 1, …, x 13]T l y = a 1*x 1+a")
- Slides: 51
Least Square Method Line fitting Hyper-plane fitting Function approximation Adavanced Numerical Computation 2008, AM NDHU 1
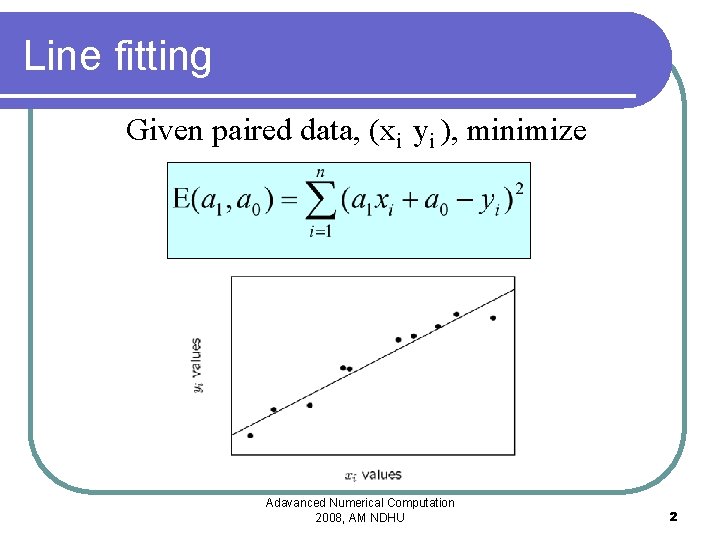
Line fitting Given paired data, (xi yi ), minimize Adavanced Numerical Computation 2008, AM NDHU 2
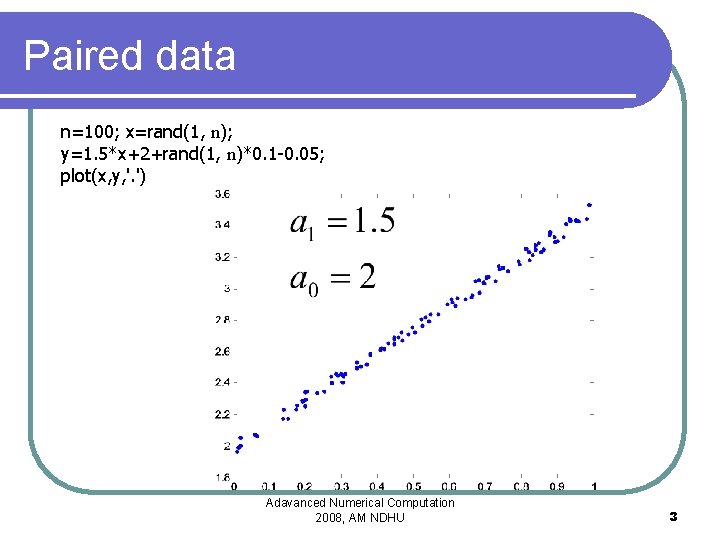
Paired data n=100; x=rand(1, n); y=1. 5*x+2+rand(1, n)*0. 1 -0. 05; plot(x, y, '. ') Adavanced Numerical Computation 2008, AM NDHU 3
Fitting criteria Adavanced Numerical Computation 2008, AM NDHU 4
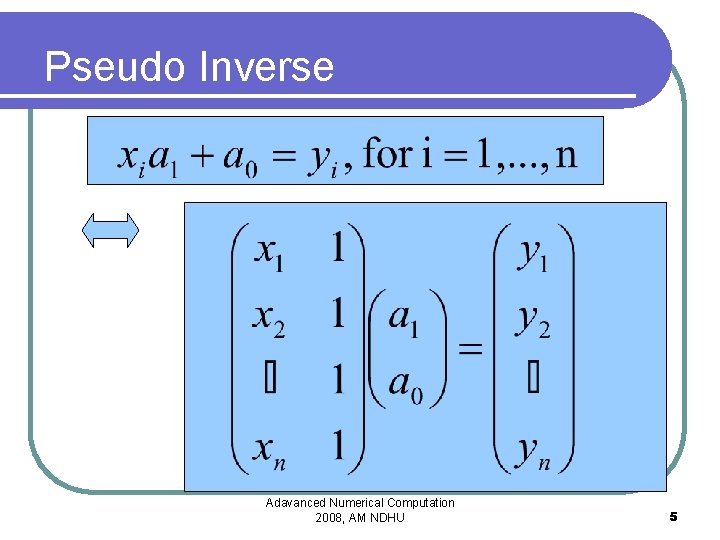
Pseudo Inverse Adavanced Numerical Computation 2008, AM NDHU 5
Form X and b X=[x' ones(n, 1)]; b=y'; Adavanced Numerical Computation 2008, AM NDHU 6
Line fitting >> a=inv(X'*X)*X'*b a= 1. 4816 2. 0113 Adavanced Numerical Computation 2008, AM NDHU 7
Line fitting >> a=pinv(X)*b a= 1. 4816 2. 0113 Adavanced Numerical Computation 2008, AM NDHU 8
Demo_line_fitting demo_line_fitting. m Adavanced Numerical Computation 2008, AM NDHU 9
Stand alone executable file mcc -m demo_line_fitting. exe demo_line_fitting. ctf Adavanced Numerical Computation 2008, AM NDHU 10
Linear system Adavanced Numerical Computation 2008, AM NDHU 11
m=n l If X is invertible Adavanced Numerical Computation 2008, AM NDHU 12
inv >> X=rand(5, 5); b=rand(5, 1); >> a=inv(X)*b a= -2. 2355 9. 2038 -7. 0138 -2. 8158 13. 3273 Adavanced Numerical Computation 2008, AM NDHU 13
Mean Square Error >> mean((X*a-b). ^2) ans = 1. 2843 e-031 Adavanced Numerical Computation 2008, AM NDHU 14
m<n l Unknown number less than constraint or data number l Minimization of the mean square error Adavanced Numerical Computation 2008, AM NDHU 15
Adavanced Numerical Computation 2008, AM NDHU 16
Pseudo Inverse Adavanced Numerical Computation 2008, AM NDHU 17
Mean square errors Adavanced Numerical Computation 2008, AM NDHU 18
Minimization Adavanced Numerical Computation 2008, AM NDHU 19
Derivative Adavanced Numerical Computation 2008, AM NDHU 20
Vector Form Adavanced Numerical Computation 2008, AM NDHU 21
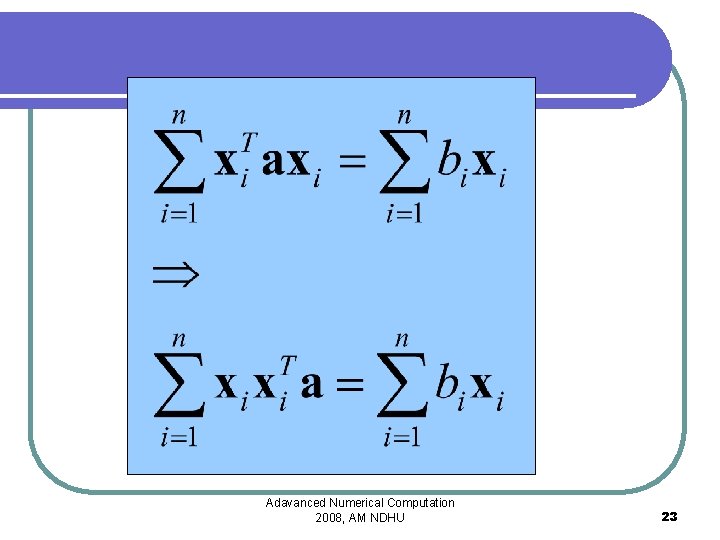
Linear system: normal equations Adavanced Numerical Computation 2008, AM NDHU 22
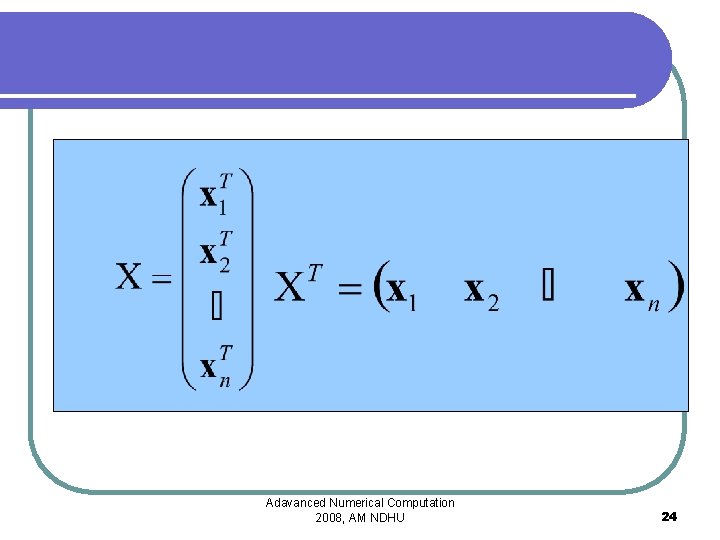
Adavanced Numerical Computation 2008, AM NDHU 23
Adavanced Numerical Computation 2008, AM NDHU 24
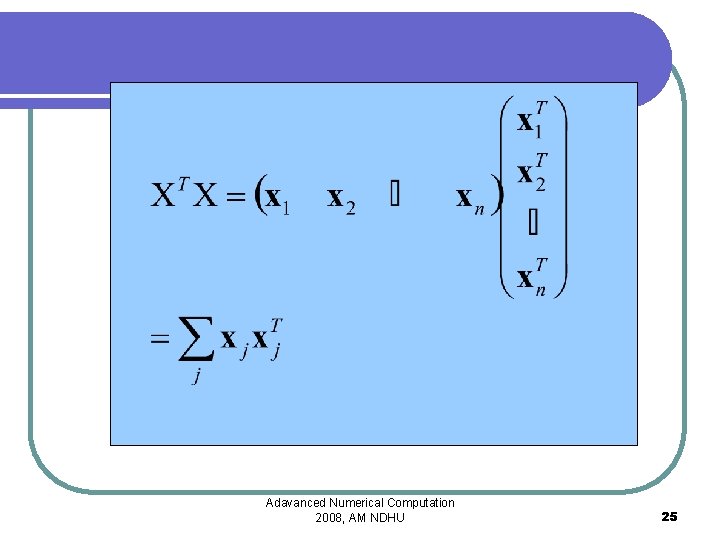
Adavanced Numerical Computation 2008, AM NDHU 25
Adavanced Numerical Computation 2008, AM NDHU 26
Adavanced Numerical Computation 2008, AM NDHU 27
Hyper-plane fitting Adavanced Numerical Computation 2008, AM NDHU 28
Mean square error 1 Adavanced Numerical Computation 2008, AM NDHU 29
Adavanced Numerical Computation 2008, AM NDHU 30
Hyper-plane fitting Step 1. Input paired data, (xi , yi), i=1…n l Step 2. Form matrix X and vector b l Step 3. Set a to pinv(X)*b l Step 4. Set a 2 to l Adavanced Numerical Computation 2008, AM NDHU 31
>> >> n=30; X=rand(n, 2); b=rand(n, 1); X=[X ones(n, 1)]; a=pinv(X)*b; aa=inv(X'*X)*(X'*b); sum(abs(a-aa)) ans = 1. 0547 e-015 Adavanced Numerical Computation 2008, AM NDHU 32
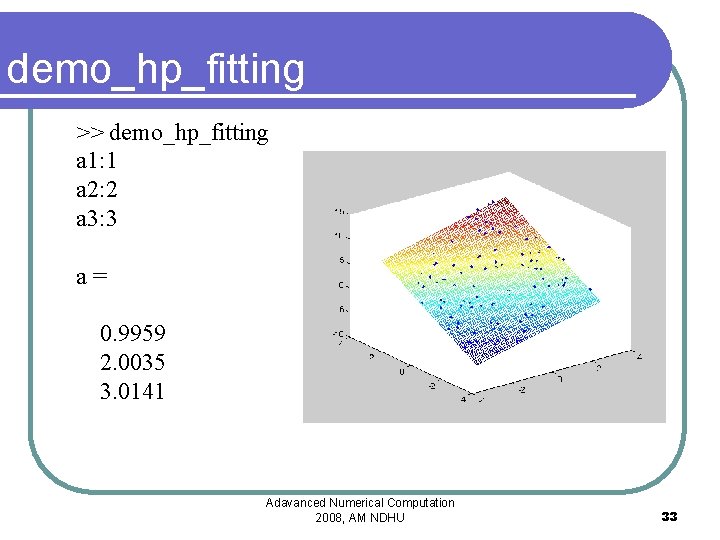
demo_hp_fitting >> demo_hp_fitting a 1: 1 a 2: 2 a 3: 3 a= 0. 9959 2. 0035 3. 0141 Adavanced Numerical Computation 2008, AM NDHU 33
HP Tool Adavanced Numerical Computation 2008, AM NDHU 34
HP Tool MLP_Tool. m MLP_Tool. fig Adavanced Numerical Computation 2008, AM NDHU 35
Mesh fstr=input('input a 2 D function: x 1. ^2+x 2. ^2+cos(x 1) : ', 's'); fx=inline(fstr); range=2*pi; x 1=-range: 0. 1: range; x 2=x 1; for i=1: length(x 1) C(i, : )=fx(x 1(i), x 2); end mesh(x 1, x 2, C); Adavanced Numerical Computation 2008, AM NDHU 36
Post-nonlinear Projection tanh Adavanced Numerical Computation 2008, AM NDHU y 37
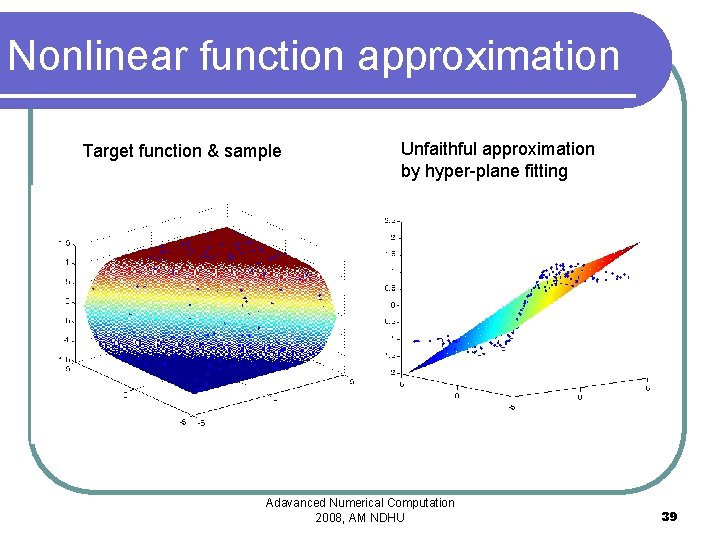
Nonlinear function approximation Adavanced Numerical Computation 2008, AM NDHU 38
Nonlinear function approximation Target function & sample Unfaithful approximation by hyper-plane fitting Adavanced Numerical Computation 2008, AM NDHU 39
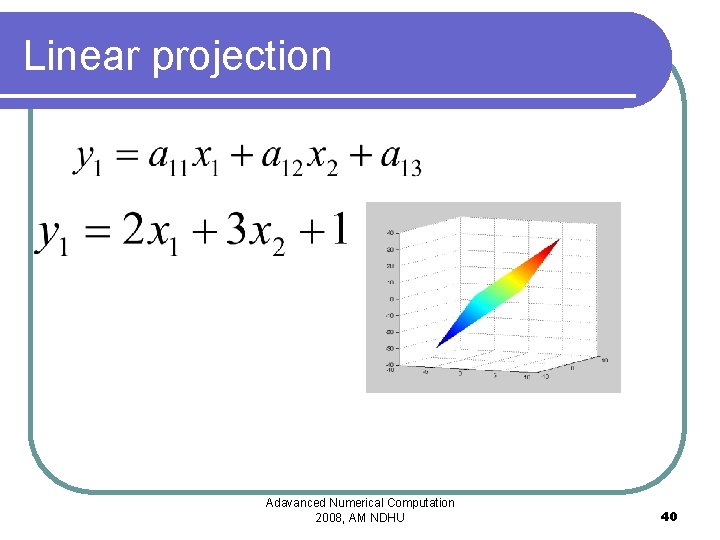
Linear projection Adavanced Numerical Computation 2008, AM NDHU 40
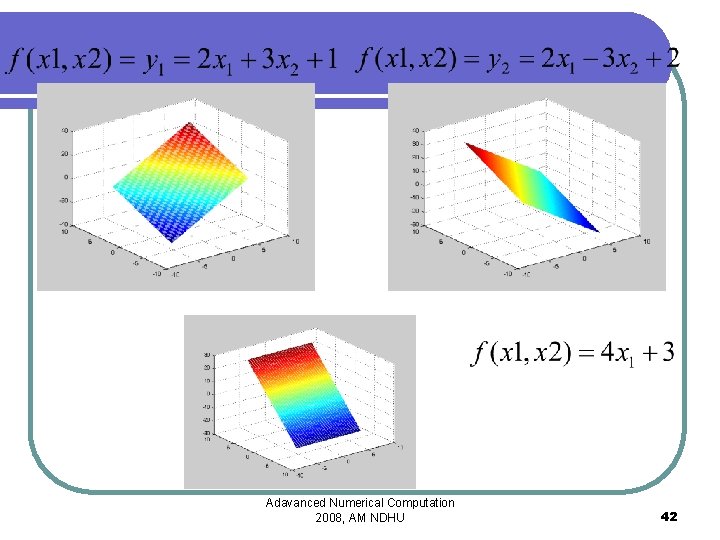
Two linear projections l Add two linear projections Adavanced Numerical Computation 2008, AM NDHU 41
Adavanced Numerical Computation 2008, AM NDHU 42
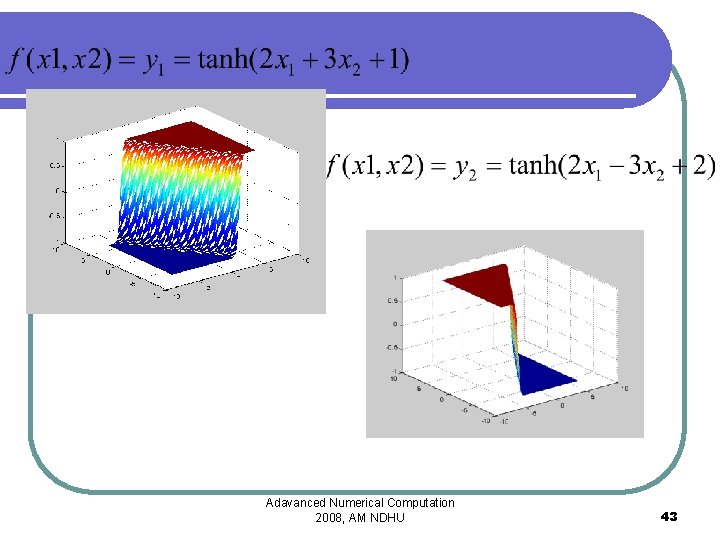
Adavanced Numerical Computation 2008, AM NDHU 43
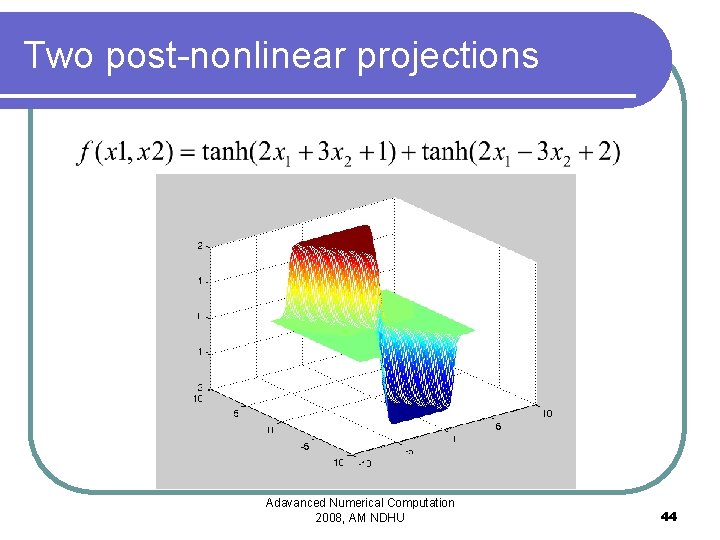
Two post-nonlinear projections Adavanced Numerical Computation 2008, AM NDHU 44
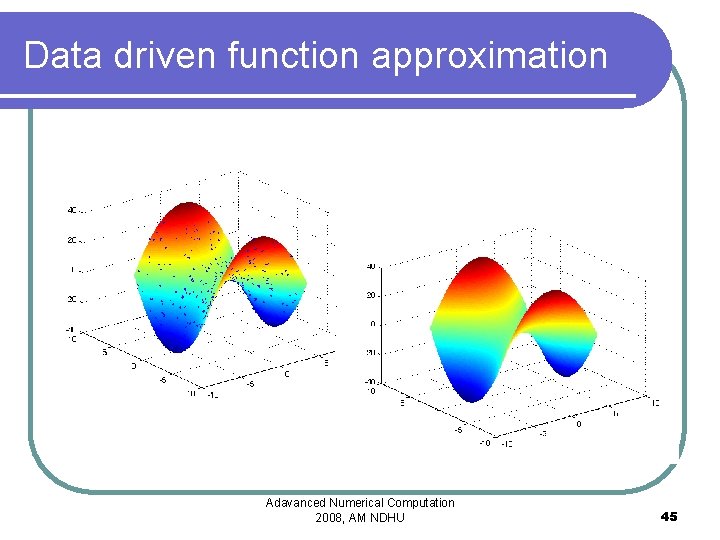
Data driven function approximation Adavanced Numerical Computation 2008, AM NDHU 45
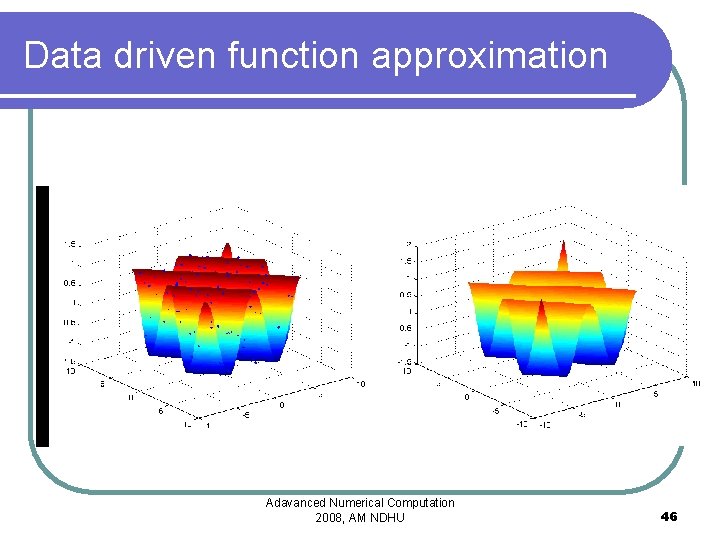
Data driven function approximation Adavanced Numerical Computation 2008, AM NDHU 46
Classification l Discriminate l analysis Linear discriminate analysis l win. dat 178 paired data l (x, y) l x {R 13} : predictor or future l y { 1, 2, 3} : three categories l Adavanced Numerical Computation 2008, AM NDHU 47
Linear assumption Predictor x=[x 1, …, x 13]T l y = a 1*x 1+a 2*x 2+…+a 13*x 13 l Find a to l Adavanced Numerical Computation 2008, AM NDHU 48
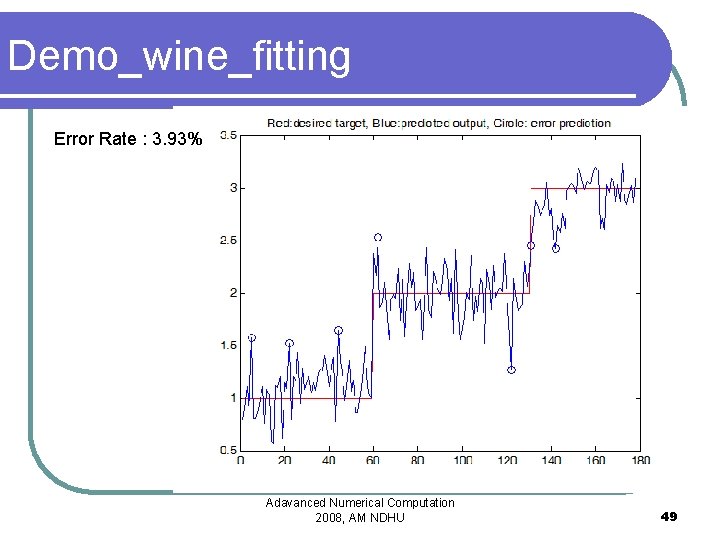
Demo_wine_fitting Error Rate : 3. 93% Adavanced Numerical Computation 2008, AM NDHU 49
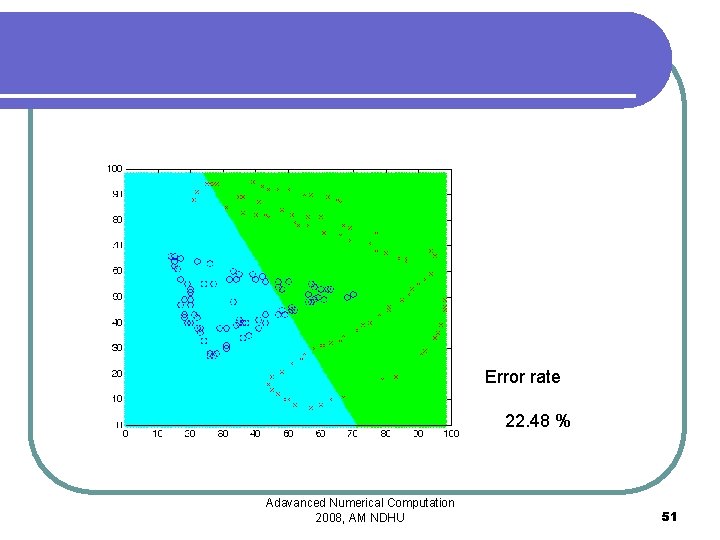
Linearly non-separable • Classify blue and red dots to two category • Linearly non-separable by hyper-plane fitting Adavanced Numerical Computation 2008, AM NDHU 50
Error rate 22. 48 % Adavanced Numerical Computation 2008, AM NDHU 51