Lecture 12 Projection and Least Square Approximation ShangHua

Lecture 12 Projection and Least Square Approximation Shang-Hua Teng

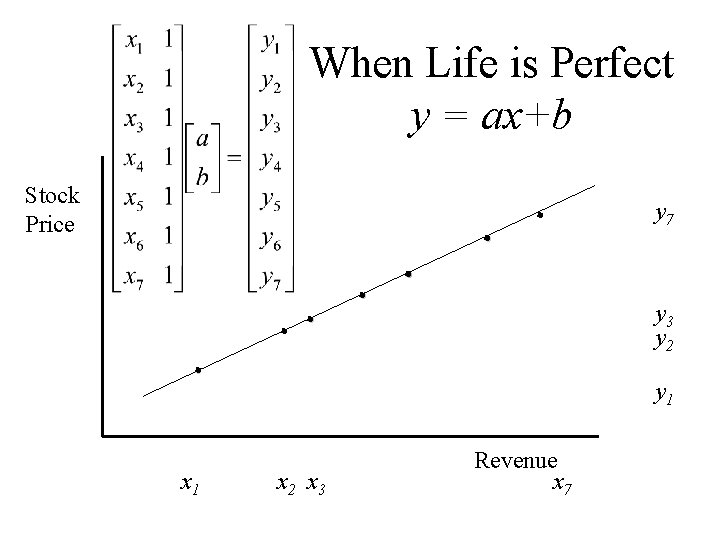
Line Fitting and Predication • Input: Table of paired data values (x, y) – – Some connection between x and y. Example: height ------ weight Example: revenue ------ stock price Example: Yesterday’s temperature at Pittsburgh ----- today’s temperature at Boston • Output: a and b that best predicates y from x: y = ax + b

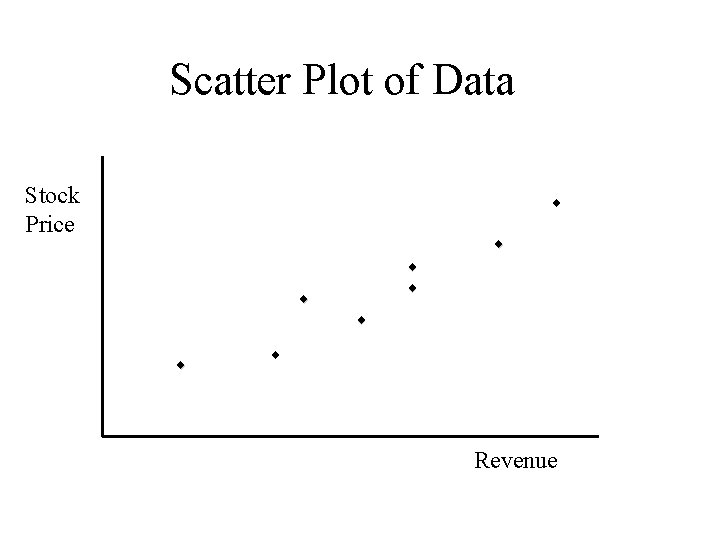
Scatter Plot of Data Stock Price ¨ ¨ ¨ ¨ Revenue

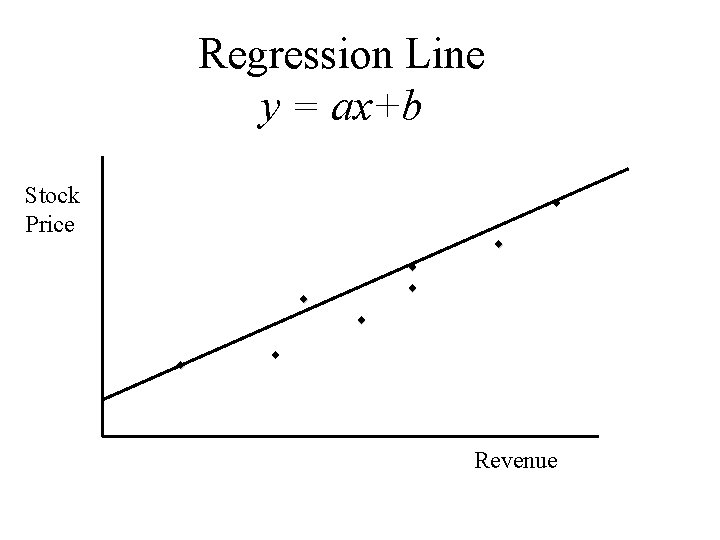
Regression Line y = ax+b Stock Price ¨ ¨ ¨ ¨ Revenue

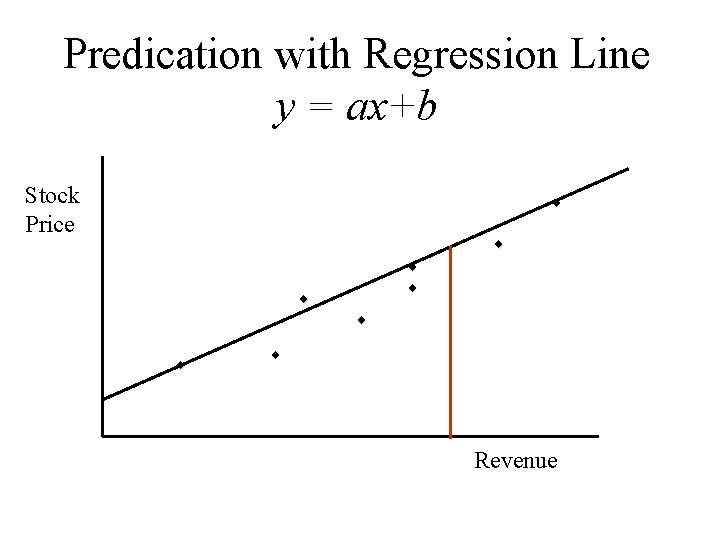
Predication with Regression Line y = ax+b Stock Price ¨ ¨ ¨ ¨ Revenue

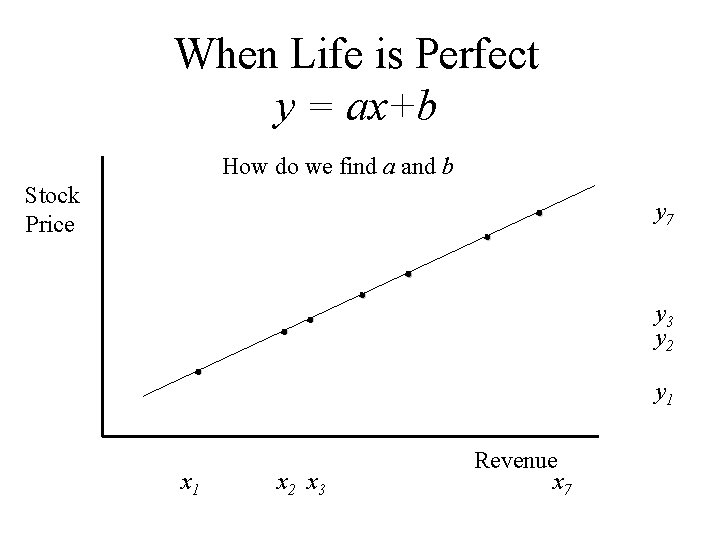
When Life is Perfect y = ax+b How do we find a and b Stock Price ¨ y 7 ¨ ¨ y 3 y 2 ¨ ¨ x 1 y 1 x 2 x 3 Revenue x 7

When Life is Perfect y = ax+b Stock Price ¨ y 7 ¨ ¨ y 3 y 2 ¨ ¨ x 1 y 1 x 2 x 3 Revenue x 7

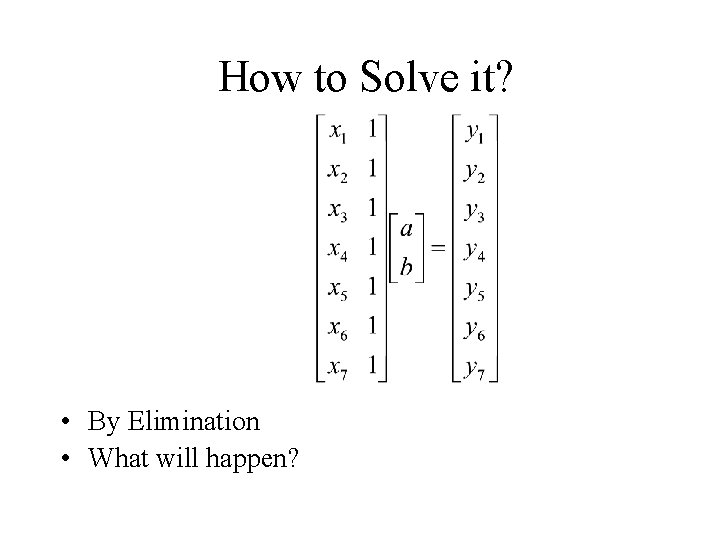
How to Solve it? • By Elimination • What will happen?

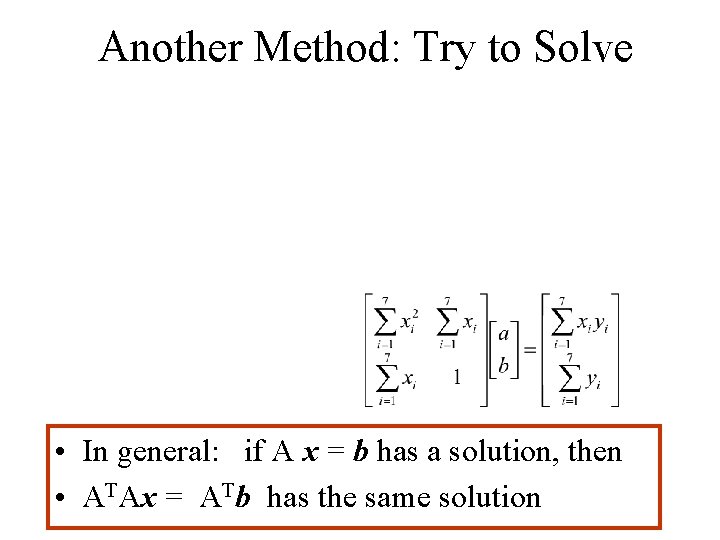
Another Method: Try to Solve • In general: if A x = b has a solution, then • ATAx = ATb has the same solution

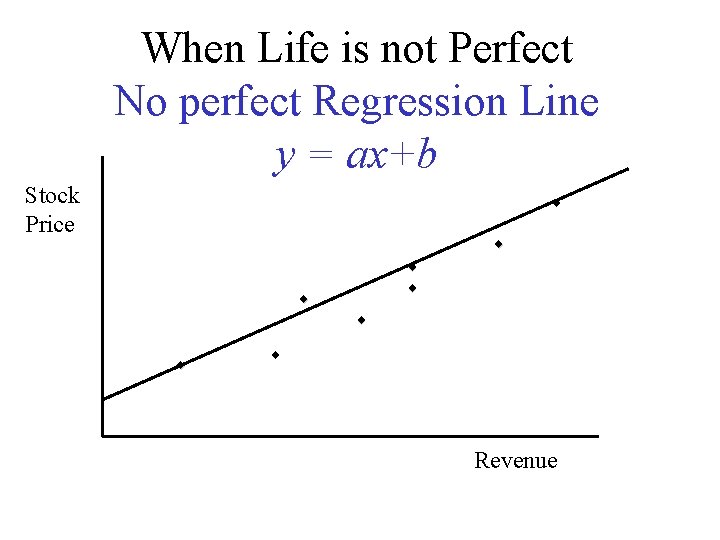
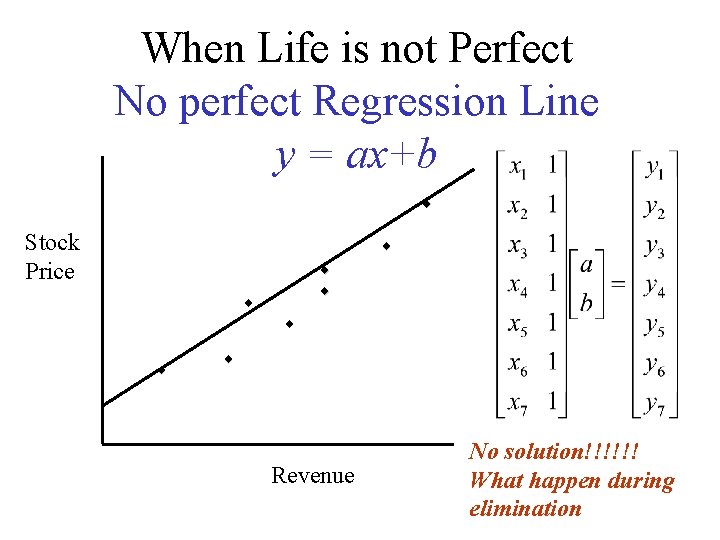
When Life is not Perfect No perfect Regression Line y = ax+b Stock Price ¨ ¨ ¨ ¨ Revenue

When Life is not Perfect No perfect Regression Line y = ax+b ¨ Stock Price ¨ ¨ ¨ ¨ Revenue No solution!!!!!! What happen during elimination

Linear Algebra Magic • In general: if A x = b has no solution, then • ATAx = ATb gives the best approximation

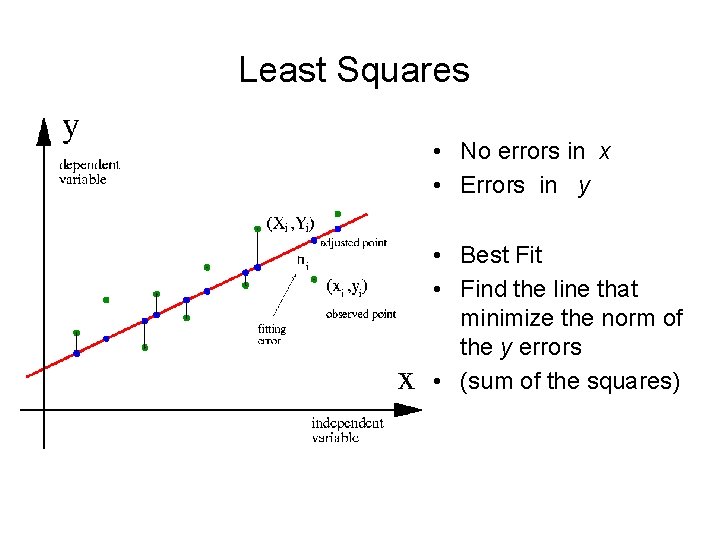
Least Squares • No errors in x • Errors in y • Best Fit • Find the line that minimize the norm of the y errors • (sum of the squares)

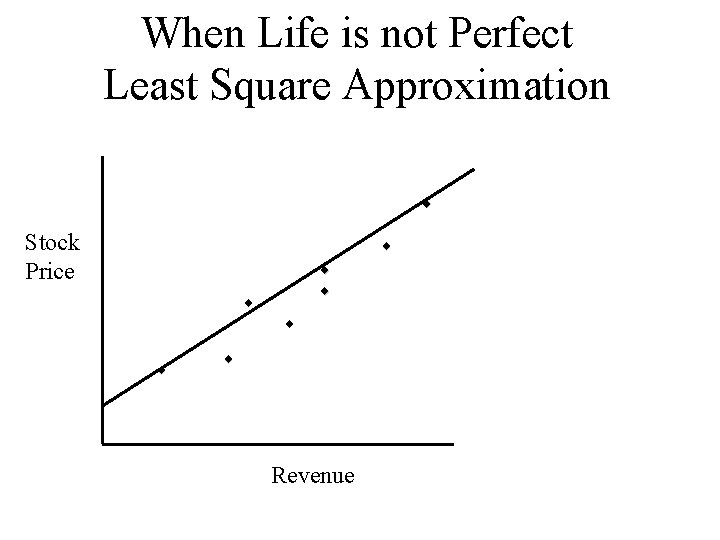
When Life is not Perfect Least Square Approximation ¨ Stock Price ¨ ¨ ¨ ¨ Revenue

In General: When Ax = b Does not Have Solution • Residue error • Least Square Approximation: Find the best

One Dimension

One Dimension

In General

In General

Least Square Approximation • In general: if A x = b has no solution, then Solving ATAx = ATb produces the least square approximation

Polynomial Regression • Minimize the residual between the data points and the curve -- least-squares regression Data Linear Quadratic Parabola Cubic General Find values of a 0 , a 1, a 2, … am

Polynomial Regression • Linear Equations • Residual • Sum of squared residuals

Least Square Solution • Normal Equations

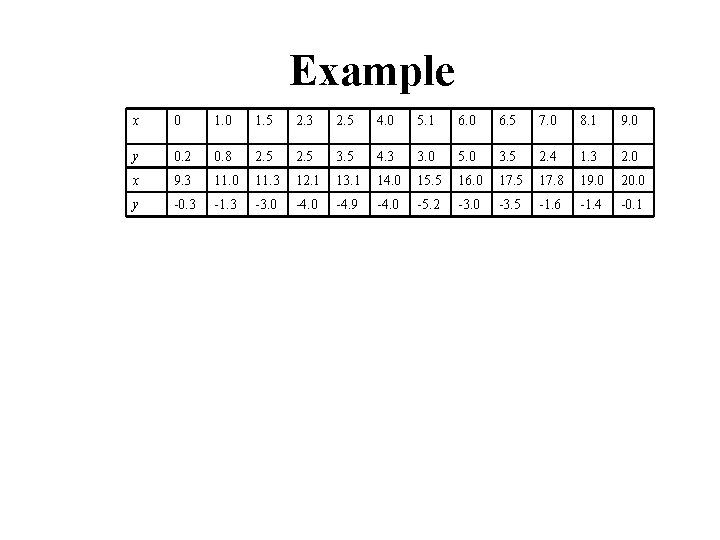
Example x 0 1. 5 2. 3 2. 5 4. 0 5. 1 6. 0 6. 5 7. 0 8. 1 9. 0 y 0. 2 0. 8 2. 5 3. 5 4. 3 3. 0 5. 0 3. 5 2. 4 1. 3 2. 0 x 9. 3 11. 0 11. 3 12. 1 13. 1 14. 0 15. 5 16. 0 17. 5 17. 8 19. 0 20. 0 y -0. 3 -1. 3 -3. 0 -4. 9 -4. 0 -5. 2 -3. 0 -3. 5 -1. 6 -1. 4 -0. 1

Example

Example Regression Equation y = - 0. 359 + 2. 305 x - 0. 353 x 2 + 0. 012 x 3

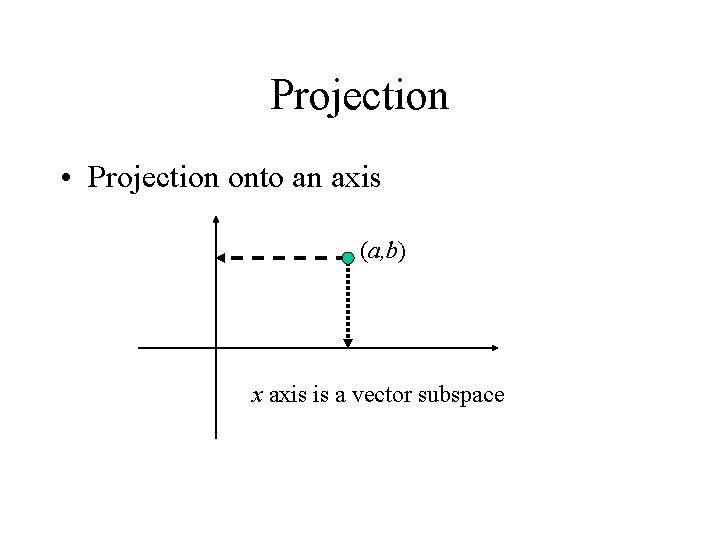
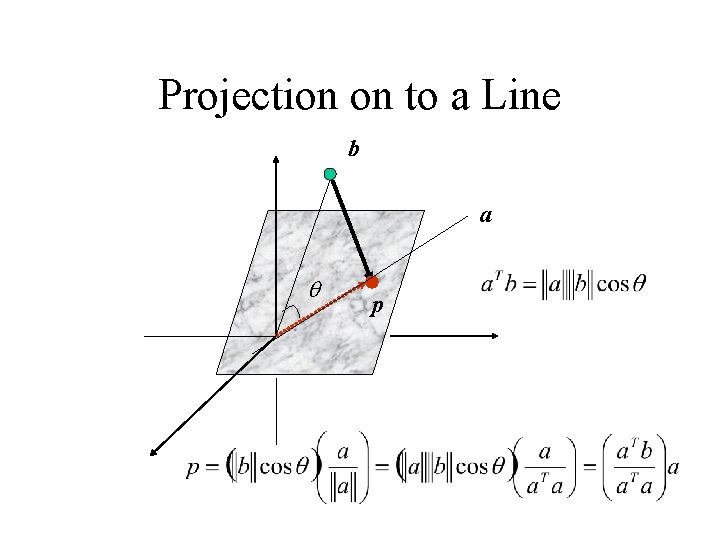
Projection • Projection onto an axis (a, b) x axis is a vector subspace

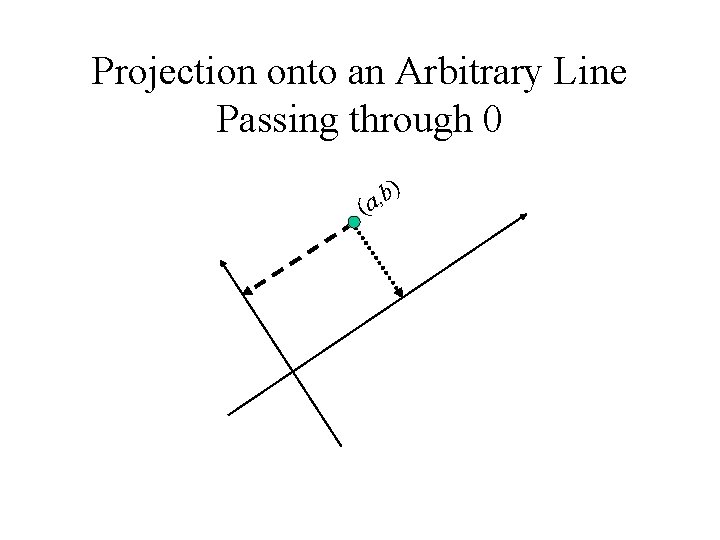
Projection onto an Arbitrary Line Passing through 0 ) b , (a

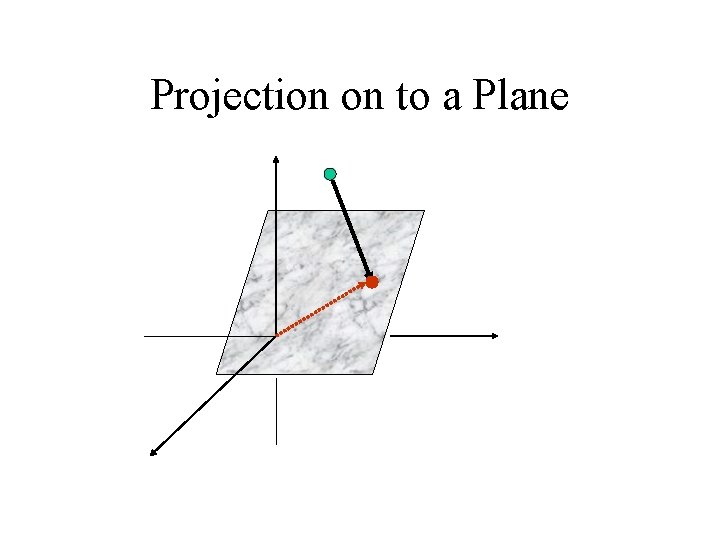
Projection on to a Plane

Projection onto a Subspace • Input: 1. Given a vector subspace V in Rm 2. A vector b in Rm… • Desirable Output: – A vector in x in V that is closest to b – The projection x of b in V – A vector x in V such that (b-x) is orthogonal to V

How to Describe a Vector Subspace V in Rm • If dim(V) = n, then V has n basis vectors – a 1, a 2, …, an – They are independent • V = C(A) where A = [a 1, a 2, …, an]

Projection onto a Subspace • Input: 1. Given n independent vectors a 1, a 2, …, an in Rm 2. A vector b in Rm… • Desirable Output: – – – A vector in x in C([a 1, a 2, …, an]) that is closest to b The projection x of b in C([a 1, a 2, …, an]) A vector x in V such that (b-x) is orthogonal to C([a 1, a 2, …, an])

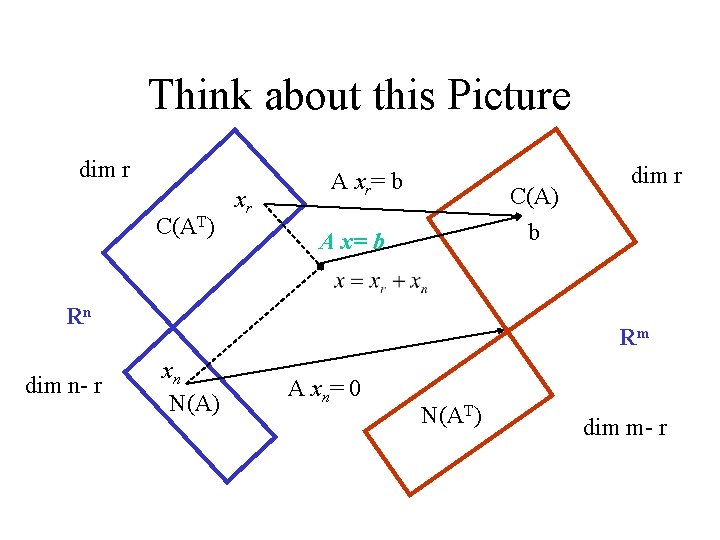
Think about this Picture dim r C(AT) xr A x r= b C(A) b A x= b Rn dim n- r dim r Rm xn N(A) A xn= 0 N(AT) dim m- r

Projection on to a Line b a q p

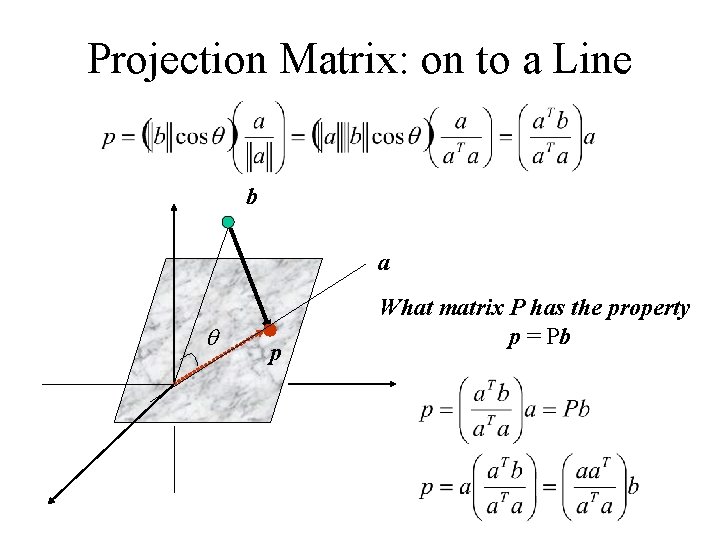
Projection Matrix: on to a Line b a q p What matrix P has the property p = Pb