kola slo projektu Nzev projektu slo a nzev

Škola: Číslo projektu: Název projektu: Číslo a název šablony klíčové aktivity: Tematická oblast: Gymnázium Václava Hlavatého, Louny, Poděbradova 661, příspěvková organizace CZ. 1. 07/1. 5. 00/34. 0616 Inovace výuky EU-8 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Volitelný předmět matematika (matematický seminář) EU-8 -63 – DERIVACE FUNKCE XIX (průběh funkce – co vás čeká na VŠ? ) Anotace Na sedmi podrobně řešených příkladech si mohou žáci procvičit úlohy o průběhu funkce. Učiteli se nabízí úlohy pro individuální, skupinovou či domácí práci žáků. Úlohy jsou ukázkou toho, co čeká absolventy gymnázií v prvním semestru vysokoškolské matematiky – úvodu do matematické analýzy. Autor Paed. Dr. Milan Rieger Jazyk Čeština Očekávaný výstup Klíčová slova Druh učebního materiálu Druh interaktivity Cílová skupina Žák dovede aplikovat získané poznatky diferenciálního počtu na zjištění průběhu funkcí. Průběh funkce, parametrická rovnice přímky, obecná rovnice přímky. Pracovní list / Animace / Obrázky / Testy Aktivita / Výklad / Test / Kombinace Žák Stupeň a typ vzdělávání Střední vzdělávání Typická věková skupina 17 – 19 let Datum vytvoření 2. 1. 2014

4ŘEŠENÉ ÚLOHY – PRŮBĚH FUNKCE 1) Určete a, b R v rovnici funkce f: y = a x 2 + b x tak, aby měla funkce f v bodě T [1; 2] ostrý lokální extrém. Potom vyšetřete průběh funkce f. 2) Určete a, b R v rovnici funkce f: y = a x 3 + b x 2 tak, aby měla funkce f v bodě T [1; 2] inflexní bod. Potom vyšetřete průběh funkce f. Vyšetřete průběh funkce f. 7) 3) 4) 5) 6) Sestrojte graf funkce f. Ukažte, že funkce f má tři inflexní body, které leží na jedné přímce.

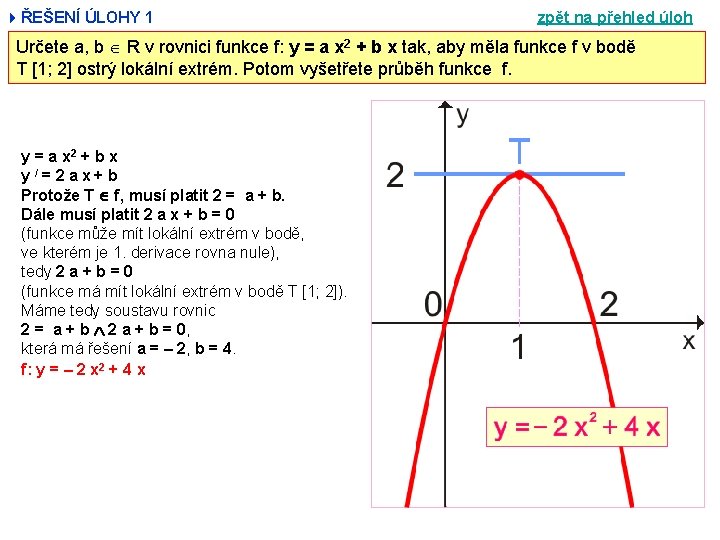
4ŘEŠENÍ ÚLOHY 1 zpět na přehled úloh Určete a, b R v rovnici funkce f: y = a x 2 + b x tak, aby měla funkce f v bodě T [1; 2] ostrý lokální extrém. Potom vyšetřete průběh funkce f. y = a x 2 + b x y / = 2 a x+ b Protože T f, musí platit 2 = a + b. Dále musí platit 2 a x + b = 0 (funkce může mít lokální extrém v bodě, ve kterém je 1. derivace rovna nule), tedy 2 a + b = 0 (funkce má mít lokální extrém v bodě T [1; 2]). Máme tedy soustavu rovnic 2 = a + b 2 a + b = 0, která má řešení a = – 2, b = 4. f: y = – 2 x 2 + 4 x

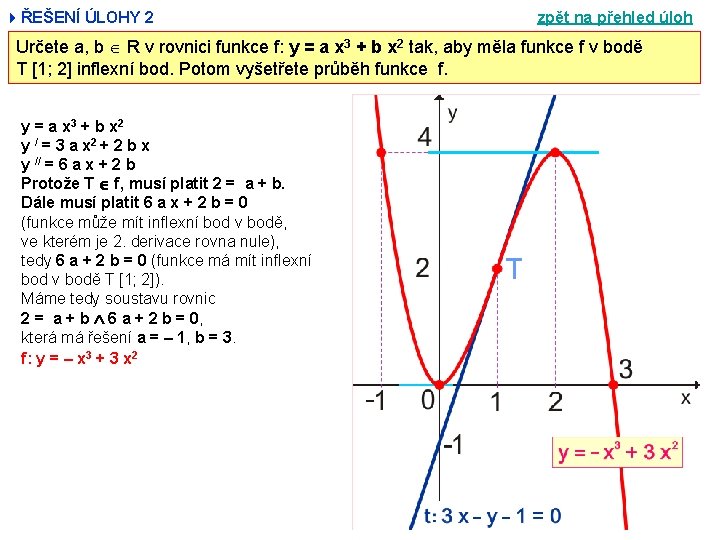
4ŘEŠENÍ ÚLOHY 2 zpět na přehled úloh Určete a, b R v rovnici funkce f: y = a x 3 + b x 2 tak, aby měla funkce f v bodě T [1; 2] inflexní bod. Potom vyšetřete průběh funkce f. y = a x 3 + b x 2 y / = 3 a x 2 + 2 b x y // = 6 a x + 2 b Protože T f, musí platit 2 = a + b. Dále musí platit 6 a x + 2 b = 0 (funkce může mít inflexní bod v bodě, ve kterém je 2. derivace rovna nule), tedy 6 a + 2 b = 0 (funkce má mít inflexní bod v bodě T [1; 2]). Máme tedy soustavu rovnic 2 = a + b 6 a + 2 b = 0, která má řešení a = – 1, b = 3. f: y = – x 3 + 3 x 2

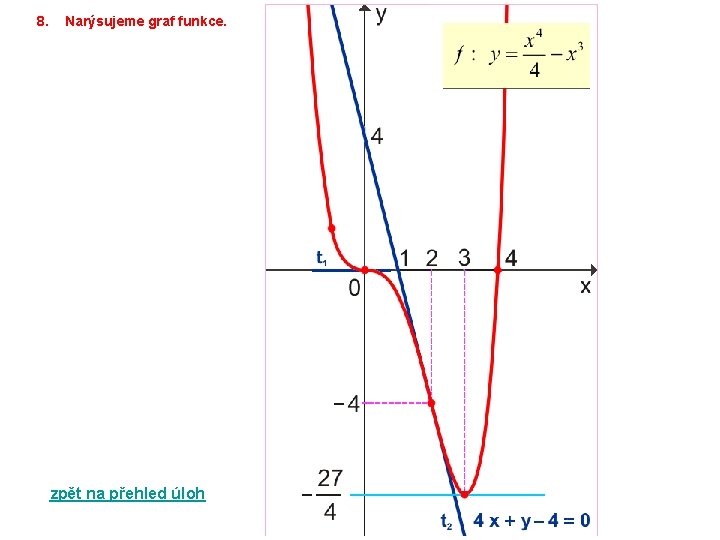
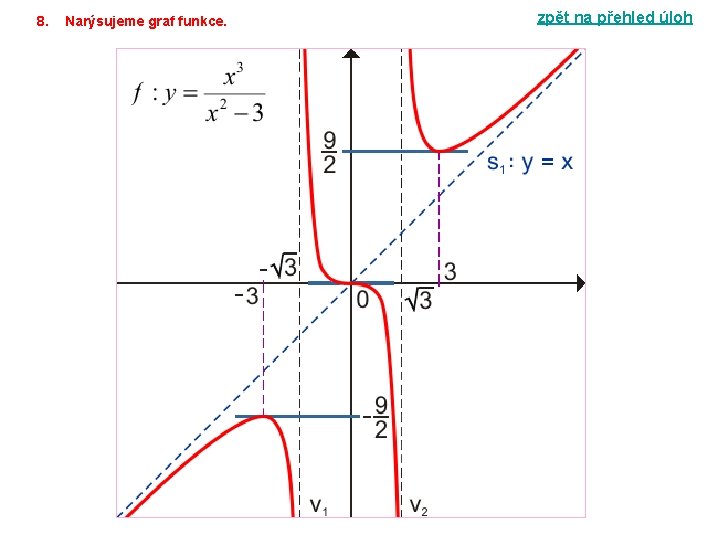
4ŘEŠENÍ ÚLOHY 3 zpět na přehled úloh Vyšetřete průběh funkce f. 1. Určíme definiční obor funkce. D(f) = R 2. Zjistíme průsečíky funkce s osami souřadnými. 3. Zjistíme, zda je funkce omezená (zdola, shora, oboustranně), sudá, lichá, periodická. Funkce f není omezenou, lichou, sudou ani periodickou funkcí v D(f). 4. Vypočítáme limity funkce v bodech nespojitosti a v nevlastních bodech. N Funkce nemá body nespojitosti. 5. Zjistíme asymptoty bez směrnice (vertikální asymptoty) a asymptoty se směrnicí. Funkce nemá vertikální asymptoty (f je spojitá v R) ani asymptoty se směrnicí (a = + nebo a = – ).

6. Výpočtem první derivace funkce zjistíme monotónnost funkce a její lokální extrémy. y / = x 3 – 3 x 2 = x 2 ( x – 3 ) y / = 0 x 2 ( x – 3 ) = 0 (x = 0 x = 3) Body podezřelé z extrému jsou x = 0, x = 3. Zjistíme znaménko 1. derivace funkce v okolí bodů podezřelých z extrémů. Funkce f je klesající v intervalu ( – ; 3 >, rostoucí v intervalu < 3; + ). Funkce f nemá v bodě 0 lokální extrém, f(0) = 0. Funkce f má v bodě 3 ostré lokální minimum, 7. Výpočtem druhé derivace zjistíme konvexnost či konkávnost funkce, inflexní body, najdeme rovnici tečen v inflexních bodech. y // = 3 x 2 – 6 x = 3 x ( x – 2 ) y // = 0 (x = 0 x = 2) Body podezřelé z inflexe jsou x = 0, x = 2. Zjistíme znaménko 2. derivace funkce v okolí bodů podezřelých z inflexe. x ( – ; 0); f // (x) > 0 funkce f je ryze konvexní v intervalu ( – ; 0 >. x ( 2; + ); f // (x) > 0 funkce f je ryze konvexní v intervalu < 2; + ). x ( 0; 2); f // (x) < 0 funkce f je ryze konkávní v intervalu < 0; 2 >. Inflexními body jsou body T 1 [ 0; 0 ], T 2 [ 2; – 4 ]. Směrnice tečny t 1 v bodě T 1: kt 1 = y / (0) = 0 t 1 : y = 0. Směrnice tečny t 2 v bodě T 2: kt 2 = y / (2) = – 4 t 2 : y + 4 = – 4 ( x – 2 ) t 2 : 4 x + y – 4 = 0.

8. Narýsujeme graf funkce. zpět na přehled úloh

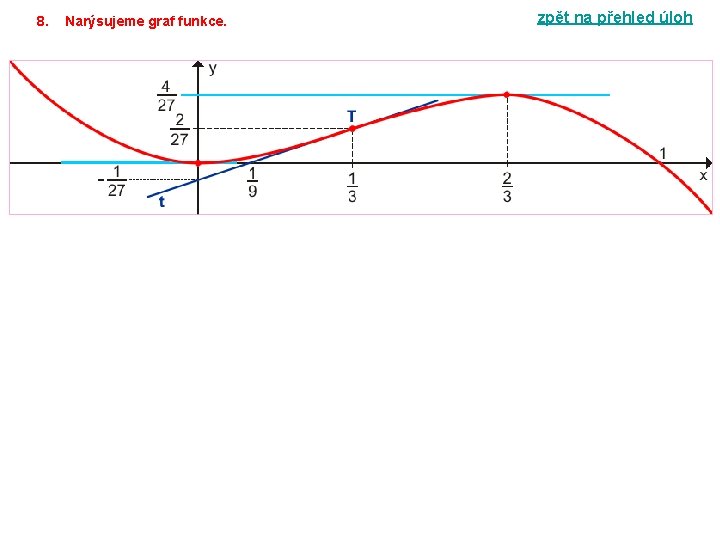
4ŘEŠENÍ ÚLOHY 4 zpět na přehled úloh Vyšetřete průběh funkce f. 1. Určíme definiční obor funkce. D(f) = R 2. Zjistíme průsečíky funkce s osami souřadnými. 3. Zjistíme, zda je funkce omezená (zdola, shora, oboustranně), sudá, lichá, periodická. Funkce f není omezenou, lichou, sudou ani periodickou funkcí v D(f). 4. Vypočítáme limity funkce v bodech nespojitosti a v nevlastních bodech. N Funkce nemá body nespojitosti. 5. Zjistíme asymptoty bez směrnice (vertikální asymptoty) a asymptoty se směrnicí. Funkce nemá vertikální asymptoty (f je spojitá v R) ani asymptoty se směrnicí ( a = – ).

6. Výpočtem první derivace funkce zjistíme monotónnost funkce a její lokální extrémy. y / = 2 x – 3 x 2 = x ( 2 – 3 x ) y / = 0 x ( 2 – 3 x ) = 0 (x = 0 x = 2 / 3) Body podezřelé z extrému jsou x = 0, x = 2 / 3. Zjistíme znaménko 1. derivace funkce v okolí bodů podezřelých z extrémů. Funkce f je klesající v intervalech ( – ; 0 >, < 2 / 3; + ), rostoucí v intervalu < 0; 2 / 3 >. Funkce f má v bodě 0 ostré lokální minimum, f(0) = 0. Funkce f má v bodě 2 / 3 ostré lokální maximum, 7. Výpočtem druhé derivace zjistíme konvexnost či konkávnost funkce, inflexní body, najdeme rovnici tečen v inflexních bodech. y // = 2 – 6 x = 2 ( 1 – 3 x ) y // = 0 x = 1 / 3 Bod podezřelý z inflexe je x = 1 / 3. Zjistíme znaménko 2. derivace funkce v okolí bodu podezřelého z inflexe. x ( – ; 1 / 3); f // (x) > 0 funkce f je ryze konvexní v intervalu ( – ; 1 / 3 >. x ( 1 / 3; + ); f // (x) < 0 funkce f je ryze konkávní v intervalu < 1 / 3; + ). Inflexním bodem je bod T. Směrnice tečny t v bodě T:

8. Narýsujeme graf funkce. zpět na přehled úloh

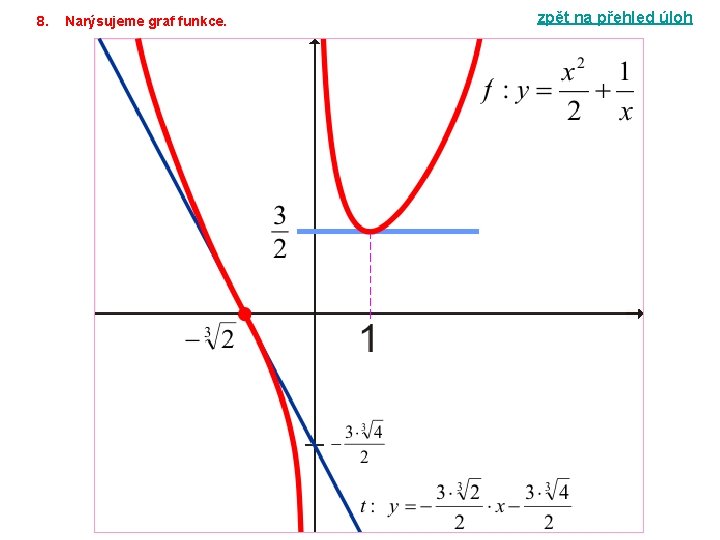
4ŘEŠENÍ ÚLOHY 5 zpět na přehled úloh Vyšetřete průběh funkce f. 1. Určíme definiční obor funkce. 2. Zjistíme průsečíky funkce s osami souřadnými. Funkce f protíná osu x i osu y v bodě [ 0; 0 ]. 3. Zjistíme, zda je funkce omezená (zdola, shora, oboustranně), sudá, lichá, periodická. Funkce f je lichou funkcí v D(f). Podle definice liché funkce platí: 1. x R; x D(f) – x D(f) 2. x D(f); – f(x) = f (– x) Pokud je funkce f lichá, můžeme vyšetřovat průběh funkce v intervalu < 0; + ). Graf funkce dorýsujeme pomocí středové souměrnosti podle počátku soustavy souřadné. 4. Vypočítáme limity funkce v bodech nespojitosti a v nevlastních bodech.

5. Zjistíme asymptoty bez směrnice (vertikální asymptoty) a asymptoty se směrnicí. Funkce f má vertikální asymtoty v 1, v 2. Funkce f má asymptotu se směrnicí s 1: y = x. 6. Výpočtem první derivace funkce zjistíme monotónnost funkce a její lokální extrémy. Body podezřelé z extrému jsou x = – 3, x = 0, x = 3. Zjistíme znaménko 1. derivace funkce v okolí bodů podezřelých z extrémů. Funkce f je rostoucí v intervalech ( – ; – 3 >, < 3; + ). Funkce f je klesající v intervalech : Funkce f nemá v bodě 0 lokální extrém f(0) = 0. Funkce f má v bodě – 3 ostré lokální maximum, v bodě 3 ostré lokální minimum.

7. Výpočtem druhé derivace zjistíme konvexnost či konkávnost funkce, inflexní body, najdeme rovnici tečen v inflexních bodech. Bod podezřelý z inflexe je x = 0. Zjistíme znaménko 2. derivace funkce v okolí bodu podezřelého z inflexe. Funkce f je ryze konvexní v intervalech Funkce f je ryze konkávní v intervalech Inflexním bodem je bod T [ 0 ; 0 ]. Směrnice tečny t v bodě T:

8. Narýsujeme graf funkce. zpět na přehled úloh

4ŘEŠENÍ ÚLOHY 6 zpět na přehled úloh Vyšetřete průběh funkce f. 1. Určíme definiční obor funkce. D(f) = R – 0 2. Zjistíme průsečíky funkce s osami souřadnými. Funkce f neprotíná osu y, protože není definována v bodě 0. 3. Zjistíme, zda je funkce omezená (zdola, shora, oboustranně), sudá, lichá, periodická. Funkce f není omezenou, lichou, sudou ani periodickou funkcí v D(f). 4. Vypočítáme limity funkce v bodech nespojitosti a v nevlastních bodech. 5. Zjistíme asymptoty bez směrnice (vertikální asymptoty) a asymptoty se směrnicí. Funkce f má vertikální asymtotu v: x = 0. Funkce f nemá asymptotu se směrnicí ( a = – a = + ).

6. Výpočtem první derivace funkce zjistíme monotónnost funkce a její lokální extrémy. Bod podezřelý z extrému je x = 1. Zjistíme znaménko 1. derivace funkce v okolí bodu podezřelého z extrému. Funkce f je rostoucí v intervalu < 1; + ). Funkce f je klesající v intervalech ( – ; 0 ) , ( 0 ; 1 >. Funkce f má v bodě 1 ostré lokální minimum

7. Výpočtem druhé derivace zjistíme konvexnost či konkávnost funkce, inflexní body, najdeme rovnici tečen v inflexních bodech. Bod podezřelý z inflexe je Zjistíme znaménko 2. derivace funkce v okolí bodu podezřelého z inflexe. Funkce f je ryze konvexní v intervalech Funkce f je ryze konkávní v intervalu Inflexním bodem je bod T. Směrnice tečny t v bodě T:

8. Narýsujeme graf funkce. zpět na přehled úloh

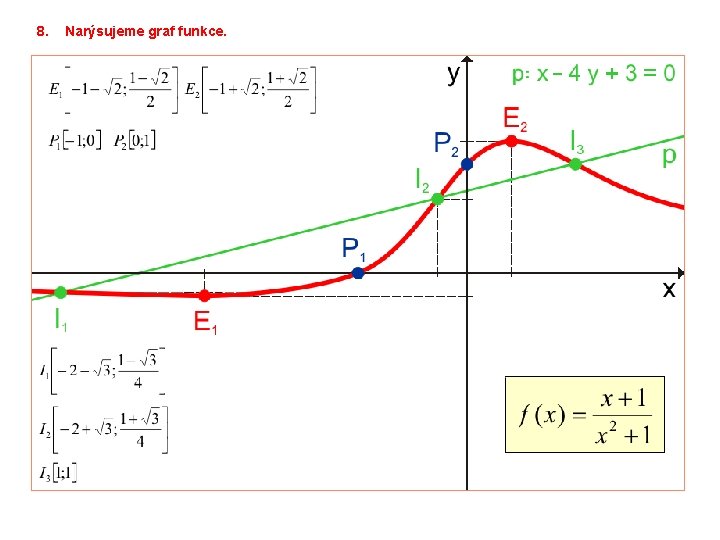
4ŘEŠENÍ ÚLOHY 7 Sbírka úloh a cvičení z matematické analýzy – Boris Pavlovič Děmidovič, vydalo nakladatelství Fragment, 1. vydání, 2003, strana 121, úloha 1308. ISBN 80 -7200 -587 -1. Sestrojte graf funkce f. Ukažte, že funkce f má tři inflexní body, které leží na jedné přímce. 1. Určíme definiční obor funkce. D(f) = R; funkce f je spojitá v R. 2. Zjistíme průsečíky funkce s osami souřadnými. 3. Zjistíme, zda je funkce omezená (zdola, shora, oboustranně), sudá, lichá, periodická. Funkce f není lichou, sudou ani periodickou funkcí v D(f). Funkce f je oboustranně omezená v D(f) Graf funkce f bude ležet v tomto rovinném pásu. 4. Vypočítáme limity funkce v nevlastních bodech. zpět na přehled úloh

5. Zjistíme asymptoty se směrnicí. Funkce f má asymptotu se směrnicí y = 0. 6. Výpočtem první derivace funkce zjistíme monotónnost funkce a její lokální extrémy. Body podezřelé z extrému jsou x 1, x 2. Zjistíme znaménko 1. derivace funkce v okolí těchto bodů. Funkce f je rostoucí v intervalu < x 2; x 1 >, klesající v intervalech ( – ; x 2 > , < x 1 ; + ). Funkce f má v bodě x 2 ostré lokální minimum Funkce f má v bodě x 1 ostré lokální maximum

7. Výpočtem druhé derivace zjistíme konvexnost či konkávnost funkce, inflexní body, najdeme rovnici tečen v inflexních bodech. Body podezřelé z inflexe jsou x 1, x 2, x 3. Zjistíme znaménko 2. derivace funkce v okolí těchto bodů. Funkce f je ryze konvexní v intervalech Funkce f je ryze konkávní v intervalu Inflexní body jsou:

8. Narýsujeme graf funkce.

9. Ukážeme, že inflexní body I 1, I 2, I 3 leží na jedné přímce. zpět na přehled úloh Určíme parametrické rovnice přímky p pomocí bodů I 2, I 3. směrový vektor přímky p parametrické rovnice přímky p obecná (neparametrická) rovnice přímky p zjistíme, zda bod I 1 leží na přímce p Inflexní body I 1, I 2, I 3 leží na jedné přímce p: x – 4 y + 3 = 0. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.