kola slo projektu Nzev projektu slo a nzev

Škola: Číslo projektu: Název projektu: Číslo a název šablony klíčové aktivity: Tematická oblast: Gymnázium Václava Hlavatého, Louny, Poděbradova 661, příspěvková organizace CZ. 1. 07/1. 5. 00/34. 0616 Inovace výuky EU-8 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Volitelný předmět matematika (matematický seminář) EU-8 -58 – DERIVACE FUNKCE XIV (konvexnost a konkávnost funkce) Anotace Definice funkce konvexní a konkávní v bodě i v intervalu. Použití při řešení úloh o průběhu funkcí. Animace jako důležitý prostředek pochopení lokálního významu znaménka druhé derivace. Autor Paed. Dr. Milan Rieger Jazyk Čeština Očekávaný výstup Klíčová slova Druh učebního materiálu Druh interaktivity Cílová skupina Žák rozumí definicím funkce konvexní a konkávní v bodě i v intervalu, je schopen řešit jednoduché úlohy na zjišťování konvexnosti či konkávnosti v kontextu úloh o průběhu funkce. Funkce konvexní (konkávní) v bodě, funkce konvexní (konkávní) v intervalu. Důkaz vět. Pracovní list / Animace / Obrázky / Testy Aktivita / Výklad / Test / Kombinace Žák Stupeň a typ vzdělávání Střední vzdělávání Typická věková skupina 17 – 19 let Datum vytvoření 10. 12. 2013

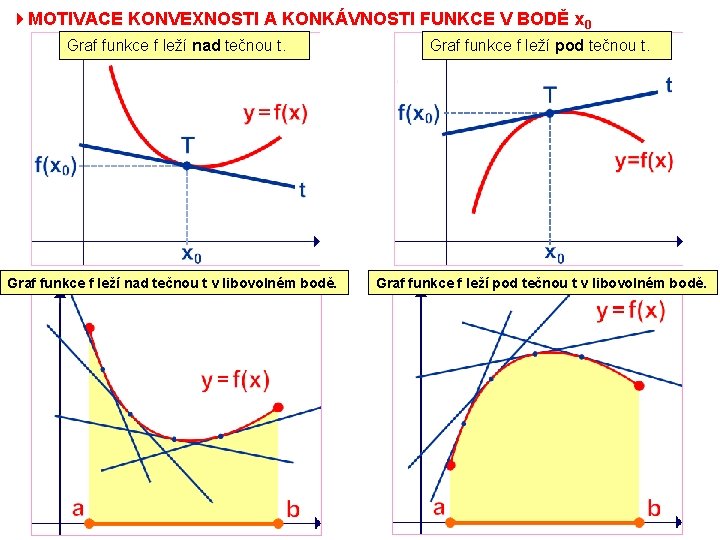
4 MOTIVACE KONVEXNOSTI A KONKÁVNOSTI FUNKCE V BODĚ x 0 Graf funkce f leží nad tečnou t. Graf funkce f leží pod tečnou t. Graf funkce f leží nad tečnou t v libovolném bodě. Graf funkce f leží pod tečnou t v libovolném bodě.

4 LOKÁLNÍ VÝZNAMÉNKA DRUHÉ DERIVACE V BODĚ x 0 Pohybující se bod [x; f(x)] je vždy nad tečnou t (pokud je x x 0). 4 DEFINICE FUNKCE RYZE KONVEXNÍ V BODĚ x 0 Předpokládejme existenci derivaci f/(x) v bodě x 0. Existuje-li > 0 tak, že pro všechna x (x 0– ; x 0) (x 0; x 0+ ) leží bod [x; f(x)] nad tečnou t, říkáme, že funkce f je ryze konvexní v bodě x 0. t: y = f(x 0) + f/(x 0). (x – x 0) leží-li bod [x; f(x)] nad tečnou t, potom platí f(x) > f(x 0) + f/(x 0). (x – x 0).

4 LOKÁLNÍ VÝZNAMÉNKA DRUHÉ DERIVACE V BODĚ x 0 Pohybující se bod [x; f(x)] je vždy pod tečnou t (pokud je x x 0). 4 DEFINICE FUNKCE RYZE KONKÁVNÍ V BODĚ x 0 Předpokládejme existenci derivaci f/(x) v bodě x 0. Existuje-li > 0 tak, že pro všechna x (x 0– ; x 0) (x 0; x 0+ ) leží bod [x; f(x)] pod tečnou t, říkáme, že funkce f je ryze konkávní v bodě x 0. t: y = f(x 0) + f/(x 0). (x – x 0) leží-li bod [x; f(x)] pod tečnou t, potom platí f(x) < f(x 0) + f/(x 0). (x – x 0).

VĚTA (lokální významénka druhé derivace funkce f v bodě x 0): Je-li f//(x 0) > 0, potom je funkce f v bodě x 0 ryze konvexní. Důkaz věty: Máme dokázat, že je funkce f v bodě x 0 ryze konvexní. Máme tedy dokázat, že existuje > 0 tak, že pro libovolné x, pro které platí 0 < x – x 0 < , leží bod [x; f(x)] nad tečnou t (tečna k funkci f v bodě [x 0; f(x 0)]). Tedy f(x) > f(x 0) + f/(x 0). (x – x 0). Z předpokladu f//(x 0) > 0 plyne, že je funkce y = f/(x) rostoucí v bodě x 0. Z toho plyne, že existuje > 0 tak, že pro (x 0 - ; x 0) platí f/( ) < f/(x 0). Pro (x 0; x 0 + ) platí f/(x 0) < f/( ). Zvolme libovolně x (x 0 - ; x 0). Podle Lagrangeovy věty (viz materiál EU-8 -54 – derivace funkce a monotónnost funkce) musí existovat číslo (x < < x 0) tak, že platí f/( ) (x – x 0) = f(x) – f(x 0). Protože je funkce y = f/(x) rostoucí v bodě x 0, platí f/( ) < f/(x 0). Pokud tuto nerovnost násobíme záporným číslem (x – x 0), dostaneme f/( ). (x – x 0) > f/(x 0). (x – x 0). Použijeme červeně označenou rovnost, dostaneme: f(x) – f(x 0) > f/(x 0). (x – x 0), odtud dostáváme f(x) > f(x 0) + f/(x 0). (x – x 0). Zvolme libovolně x (x 0; x 0 + ). Musí existovat číslo (x 0 < < x) tak, že platí f/( ) (x – x 0) = f(x) – f(x 0). Protože je funkce y = f/(x) rostoucí v bodě x 0, platí f/(x 0) < f/( ). Pokud tuto nerovnost násobíme kladným číslem (x – x 0), dostaneme f/(x 0). (x – x 0) < f/( ). (x – x 0). Použijeme červeně označenou rovnost, dostaneme: f(x) – f(x 0) > f/(x 0). (x – x 0), odtud dostáváme f(x) > f(x 0) + f/(x 0). (x – x 0). VĚTA (lokální významénka druhé derivace funkce f v bodě x 0): Je-li f//(x 0) < 0, potom je funkce f v bodě x 0 ryze konkávní. Důkaz věty bude velmi podobný předešlému důkazu.

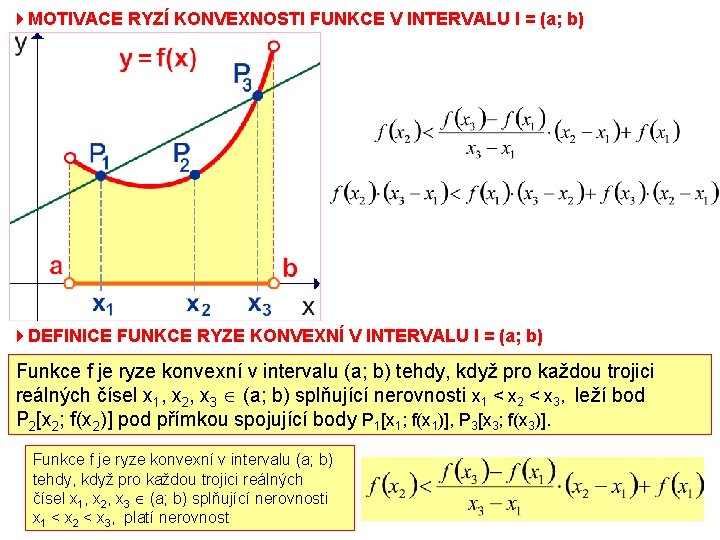
4 MOTIVACE RYZÍ KONVEXNOSTI FUNKCE V INTERVALU I = (a; b) 4 DEFINICE FUNKCE RYZE KONVEXNÍ V INTERVALU I = (a; b) Funkce f je ryze konvexní v intervalu (a; b) tehdy, když pro každou trojici reálných čísel x 1, x 2, x 3 (a; b) splňující nerovnosti x 1 < x 2 < x 3, leží bod P 2[x 2; f(x 2)] pod přímkou spojující body P 1[x 1; f(x 1)], P 3[x 3; f(x 3)]. Funkce f je ryze konvexní v intervalu (a; b) tehdy, když pro každou trojici reálných čísel x 1, x 2, x 3 (a; b) splňující nerovnosti x 1 < x 2 < x 3, platí nerovnost

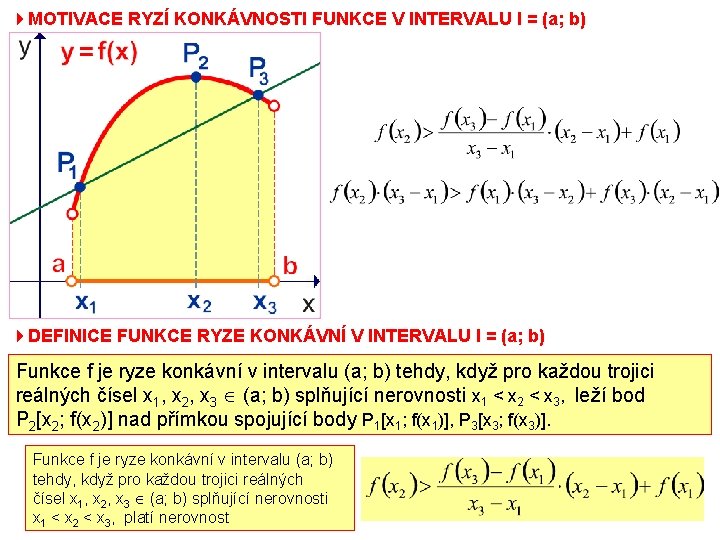
4 MOTIVACE RYZÍ KONKÁVNOSTI FUNKCE V INTERVALU I = (a; b) 4 DEFINICE FUNKCE RYZE KONKÁVNÍ V INTERVALU I = (a; b) Funkce f je ryze konkávní v intervalu (a; b) tehdy, když pro každou trojici reálných čísel x 1, x 2, x 3 (a; b) splňující nerovnosti x 1 < x 2 < x 3, leží bod P 2[x 2; f(x 2)] nad přímkou spojující body P 1[x 1; f(x 1)], P 3[x 3; f(x 3)]. Funkce f je ryze konkávní v intervalu (a; b) tehdy, když pro každou trojici reálných čísel x 1, x 2, x 3 (a; b) splňující nerovnosti x 1 < x 2 < x 3, platí nerovnost

4 VĚTA (souvislost znaménka druhé derivace funkce f a konvexnosti funkce v intervalu) Jestliže v každém bodě intervalu (a; b) platí f//(x) > 0, potom je funkce f v intervalu (a; b) ryze konvexní. Důkaz věty: Máme dokázat, že je funkce f v intervalu (a; b) ryze konvexní. Máme tedy dokázat, že pro každou trojici reálných čísel x 1, x 2, x 3 (a; b), x 1 < x 2 < x 3 platí nerovnost f(x 2) (x 3 –x 1) < f(x 1) (x 3 – x 2) + f(x 3) (x 2 – x 1). Z předpokladu f//(x 0) > 0 plyne, že je funkce y = f/(x) rostoucí v intervalu (a; b). To znamená, že pro libovolná dvě čísla , (a; b) platí, je-li < f/( ). Zvolme libovolně x 1, x 2, x 3 (a; b) tak, aby x 1 < x 2 < x 3. Podle Lagrangeovy věty (viz materiál EU-8 -54 – derivace funkce a monotónnost funkce) musí existovat číslo (x 1; x 2) tak, že platí f/( ) (x 2 – x 1) = f(x 2) – f(x 1). Dále musí existovat číslo (x 2; x 3), pro které platí f/( ) (x 3 – x 2) = f(x 3) – f(x 2). Protože je funkce y = f/(x) rostoucí v intervalu (a; b) a < , platí f/( ) < f/( ). Potom musí platit: 4 VĚTA (souvislost znaménka druhé derivace funkce f a konkávnosti funkce v intervalu) Jestliže v každém bodě intervalu (a; b) platí f//(x) < 0, potom je funkce f v intervalu (a; b) ryze konkávní. Důkaz věty bude velmi podobný předešlému důkazu.

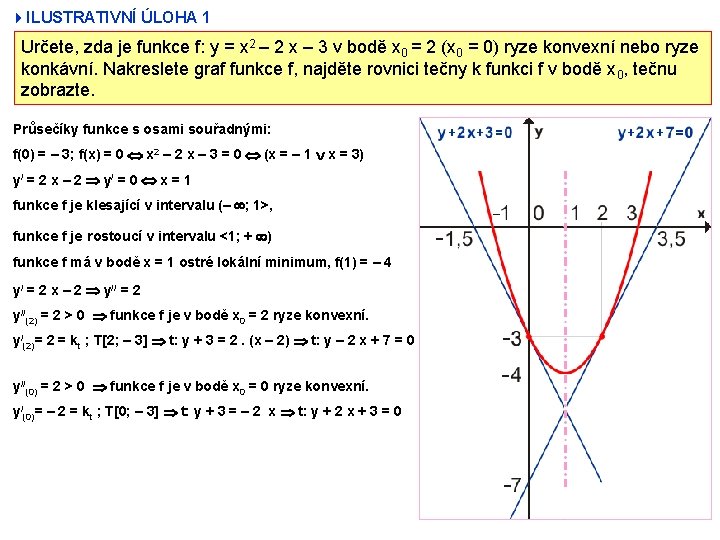
4 ILUSTRATIVNÍ ÚLOHA 1 Určete, zda je funkce f: y = x 2 – 2 x – 3 v bodě x 0 = 2 (x 0 = 0) ryze konvexní nebo ryze konkávní. Nakreslete graf funkce f, najděte rovnici tečny k funkci f v bodě x 0, tečnu zobrazte. Průsečíky funkce s osami souřadnými: f(0) = – 3; f(x) = 0 x 2 – 2 x – 3 = 0 (x = – 1 x = 3) y/ = 2 x – 2 y / = 0 x = 1 funkce f je klesající v intervalu (– ; 1>, funkce f je rostoucí v intervalu <1; + ) funkce f má v bodě x = 1 ostré lokální minimum, f(1) = – 4 y/ = 2 x – 2 y// = 2 y//(2) = 2 > 0 funkce f je v bodě x 0 = 2 ryze konvexní. y/(2)= 2 = kt ; T[2; – 3] t: y + 3 = 2. (x – 2) t: y – 2 x + 7 = 0 y//(0) = 2 > 0 funkce f je v bodě x 0 = 0 ryze konvexní. y/(0)= – 2 = kt ; T[0; – 3] t: y + 3 = – 2 x t: y + 2 x + 3 = 0

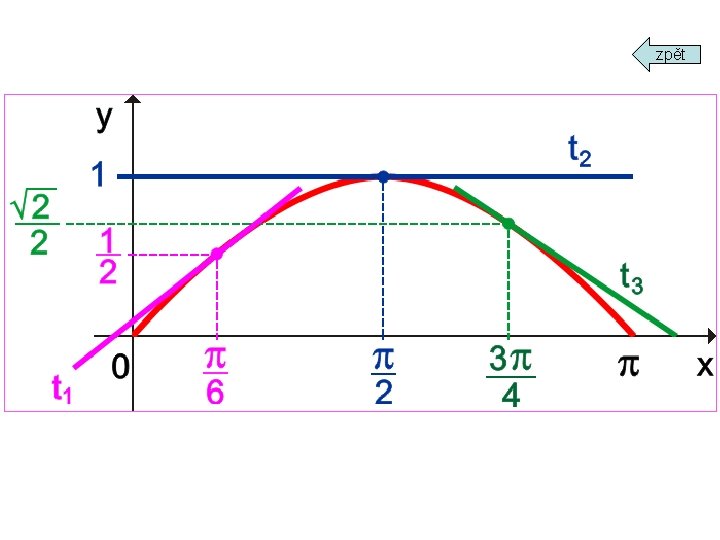
4 ILUSTRATIVNÍ ÚLOHA 2 Určete, zda je funkce f: y = sin x v bodě x 0 = /6 (x 0 = /2; x 0 = 3 /4) ryze konvexní nebo ryze konkávní. Nakreslete graf funkce f v intervalu <0; >, najděte rovnici tečny k funkci f v bodě x 0, tečnu zobrazte. funkce f je rostoucí v intervalu <0; /2> funkce f je klesající v intervalu < /2; > funkce f má v bodě x = /2 ostré lokální maximum, f( /2) = 1 y/ = cos x y// = – sin x graf

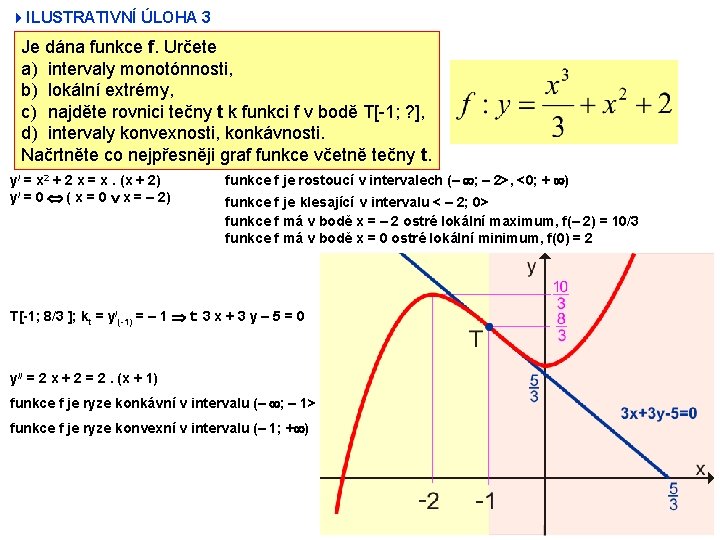
4 ILUSTRATIVNÍ ÚLOHA 3 Je dána funkce f. Určete a) intervaly monotónnosti, b) lokální extrémy, c) najděte rovnici tečny t k funkci f v bodě T[-1; ? ], d) intervaly konvexnosti, konkávnosti. Načrtněte co nejpřesněji graf funkce včetně tečny t. y/ = x 2 + 2 x = x. (x + 2) y/ = 0 ( x = 0 x = – 2) funkce f je rostoucí v intervalech (– ; – 2>, <0; + ) funkce f je klesající v intervalu < – 2; 0> funkce f má v bodě x = – 2 ostré lokální maximum, f(– 2) = 10/3 funkce f má v bodě x = 0 ostré lokální minimum, f(0) = 2 T[-1; 8/3 ]; kt = y/(-1) = – 1 t: 3 x + 3 y – 5 = 0 y// = 2 x + 2 = 2. (x + 1) funkce f je ryze konkávní v intervalu (– ; – 1> funkce f je ryze konvexní v intervalu (– 1; + )

4ÚLOHY K PROCVIČENÍ Určete, zda je funkce f: y = – x 2 – 2 x + 3 v bodě x 0 = – 2 (x 0 = 0) ryze konvexní nebo ryze konkávní. Nakreslete graf funkce f, najděte rovnici tečny k funkci f v bodě x 0, tečnu zobrazte. Určete, zda je funkce f: y = – sin x v bodě x 0 = /6 (x 0 = /2; x 0 = 3 /4) ryze konvexní nebo ryze konkávní. Nakreslete graf funkce f v intervalu <0; >, najděte rovnici tečny k funkci f v bodě x 0, tečnu zobrazte. Je dána funkce f. Určete a) intervaly monotónnosti, b) lokální extrémy, c) najděte rovnici tečny t k funkci f v bodě T[1; ? ], d) intervaly konvexnosti, konkávnosti. Načrtněte co nejpřesněji graf funkce včetně tečny t. 4 NÁROČNĚJŠÍ ÚLOHY K PROCVIČENÍ – dokažte následující věty Je-li f//(x 0) < 0, potom je funkce f v bodě x 0 ryze konkávní. Jestliže v každém bodě intervalu (a; b) platí f//(x) < 0, potom je funkce f v intervalu (a; b) ryze konkávní. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.

zpět