kola slo projektu Nzev projektu slo a nzev

Škola: Číslo projektu: Název projektu: Číslo a název šablony klíčové aktivity: Tematická oblast: Gymnázium Václava Hlavatého, Louny, Poděbradova 661, příspěvková organizace CZ. 1. 07/1. 5. 00/34. 0616 Inovace výuky EU-8 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Volitelný předmět matematika (matematický seminář) EU-8 -53 – DERIVACE FUNKCE IX (derivace exponenciálních a logaritmických funkcí) Anotace Zopakování exponenciálních, logaritmických funkcí a pojmu inverzní funkce. „Rychlé“ nalezení rovnice inverzní funkce k funkci logaritmické (exponenciální). Odvození (důkaz) derivací logaritmických a exponenciálních funkcí. Autor Paed. Dr. Milan Rieger Jazyk Čeština Očekávaný výstup Žák chápe odvození derivace exponenciálních a logaritmických funkcí, odvozené vzorce dovede používat při řešení úloh. Klíčová slova Exponenciální funkce, logaritmická funkce, inverzní funkce, derivace exponenciální a logaritmické funkce. Druh učebního materiálu Druh interaktivity Cílová skupina Pracovní list / Animace / Obrázky / Testy Aktivita / Výklad / Test / Kombinace Žák Stupeň a typ vzdělávání Střední vzdělávání Typická věková skupina 17 – 19 let Datum vytvoření 30. 1. 2013

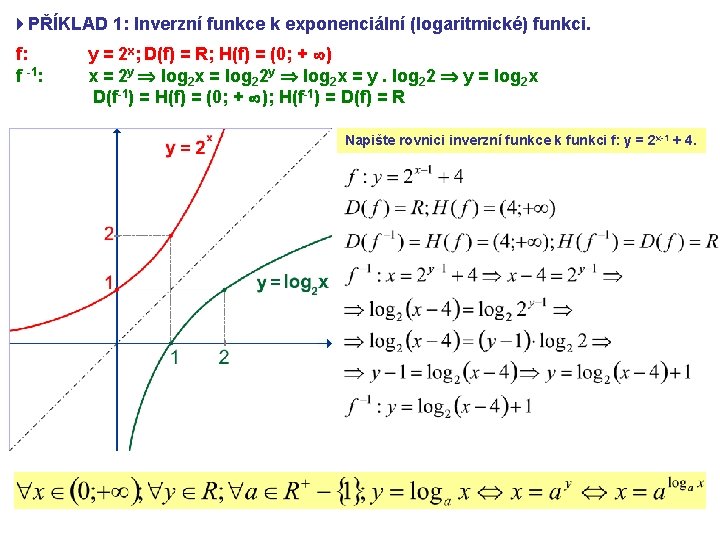
4 PŘÍKLAD 1: Inverzní funkce k exponenciální (logaritmické) funkci. f: f -1: y = 2 x; D(f) = R; H(f) = (0; + ) x = 2 y log 2 x = log 22 y log 2 x = y. log 22 y = log 2 x D(f-1) = H(f) = (0; + ); H(f-1) = D(f) = R Napište rovnici inverzní funkce k funkci f: y = 2 x-1 + 4.

4 PŘÍKLAD 2: Inverzní funkce k exponenciální (logaritmické) funkci. f: f -1: y = ex; D(f) = R; H(f) = (0; + ) x = ey logex = logeey ln x = y. ln e y = ln x D(f-1) = H(f) = (0; + ); H(f-1) = D(f) = R Napište rovnici inverzní funkce k funkci f: y = ex+1 – 3.

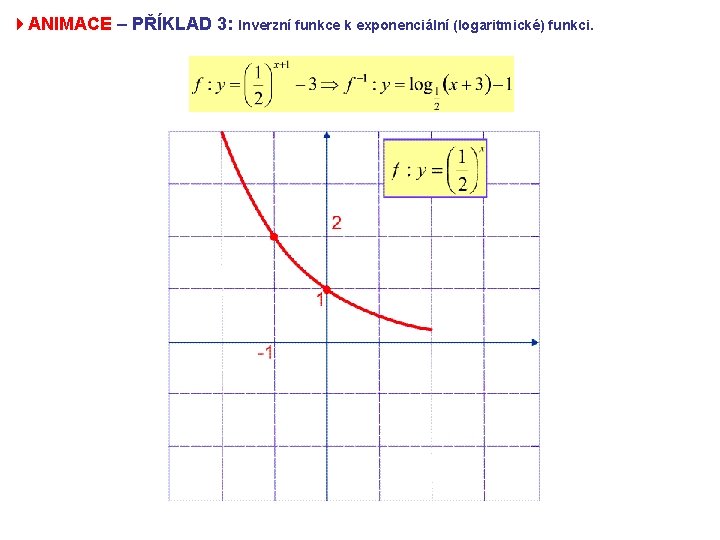
4 PŘÍKLAD 3: Inverzní funkce k exponenciální (logaritmické) funkci. f: f -1: y = 2–x =0, 5 x; D(f) = R; H(f) = (0; + ) x = 0, 5 y log 0, 5 x = log 0, 5 y log 0, 5 x = y. log 0, 5 y = log 0, 5 x D(f-1) = H(f) = (0; + ); H(f-1) = D(f) = R Napište rovnici inverzní funkce k funkci f: y = 0, 5 x+1 – 3.

4 ANIMACE – PŘÍKLAD 3: Inverzní funkce k exponenciální (logaritmické) funkci.

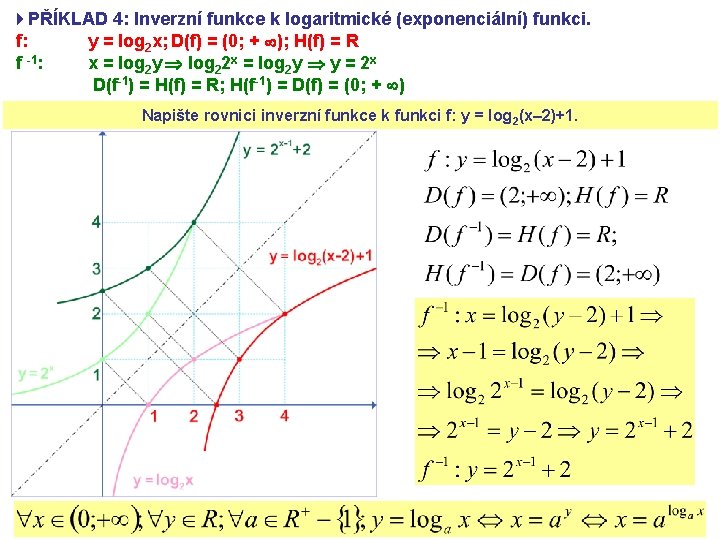
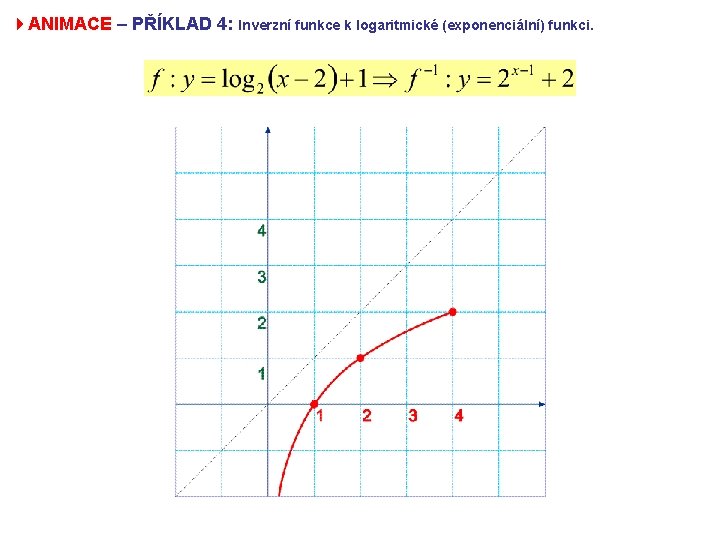
4 PŘÍKLAD 4: Inverzní funkce k logaritmické (exponenciální) funkci. f: y = log 2 x; D(f) = (0; + ); H(f) = R f -1: x = log 2 y log 22 x = log 2 y y = 2 x D(f-1) = H(f) = R; H(f-1) = D(f) = (0; + ) Napište rovnici inverzní funkce k funkci f: y = log 2(x– 2)+1.

4 ANIMACE – PŘÍKLAD 4: Inverzní funkce k logaritmické (exponenciální) funkci.

4 DERIVACE exponenciální funkce y = ex (nejdříve jedna důležitá limita)

4 DERIVACE exponenciální funkce y = ex (odvození derivace funkce pomocí definice derivace) Při odvození derivace funkce použijeme následující úvahy: x x 0 (x – x 0) 0; položíme-li h = x – x 0 h 0 Funkce y = ex se derivací nemění! y = y / = ex

4 DERIVACE exponenciální funkce y = ax Při odvození derivace funkce použijeme následující: 1. y = ln x ey = x elnx = x (definice přirozeného logaritmu); 2. dosadíme-li v rovnici elnx = x za x = a, dostaneme elna = a (a>0); 3. potom platí ax = (elna)x = ex. lna. y = ax y/ = (ax)/ = (ex lna)/ = [použitím derivace složené funkce dostaneme] = ex lna. (x. lna)/ = ex lna. [(x)/. lna + x. (lna)/ ] = [použití derivace součinu funkcí] = ex lna. [ lna + 0 ] = ex lna = ax. lna x R; a R+ – {1}; (ax)/ = ax. lna Dosadíme-li do odvozeného vzorce za a = e, dostaneme: (ex)/ = ex. lne = ex. 1 = ex.

4 DERIVACE logaritmické funkce y = logax Při odvození derivace funkce y = logax použijeme derivaci inverzní funkce y = logax x = ay x (0; + ); y R; a R+ {1} Dosadíme-li za a = e dostaneme:

4 SHRNUTÍ – DERIVACE EXPONENCIÁLNÍCH A LOGARITMICKÝCH FUNKCÍ 4 AUTOTEST – VYPOČÍTEJTE DERIVACE FUNKCÍ: Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.