kola slo projektu Nzev projektu slo a nzev

Škola: Číslo projektu: Název projektu: Číslo a název šablony klíčové aktivity: Tematická oblast: Gymnázium Václava Hlavatého, Louny, Poděbradova 661, příspěvková organizace CZ. 1. 07/1. 5. 00/34. 0616 Inovace výuky EU-8 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Volitelný předmět matematika (matematický seminář) EU-8 -54 – DERIVACE FUNKCE X (derivace funkce a monotónnost funkce) Anotace Zopakování pojmu funkce rostoucí a funkce klesající v intervalu. Rolleova a Lagrangeova věta. Souvislost znaménka první derivace funkce a monotónnosti funkce. Autor Paed. Dr. Milan Rieger Jazyk Čeština Očekávaný výstup Klíčová slova Druh učebního materiálu Druh interaktivity Cílová skupina Žák rozumí definici funkce rostoucí (klesající) v intervalu, tuto vlastnost umí aplikovat u elementárních funkcí. Žák umí na základě výpočtu první derivace funkce rozhodnout, ve kterých intervalech je daná funkce rostoucí či klesající. Funkce rostoucí, funkce klesající, první derivace funkce, znaménko první derivace funkce, monotónnost funkce, průběh funkce. Pracovní list / Animace / Obrázky / Testy Aktivita / Výklad / Test / Kombinace Žák Stupeň a typ vzdělávání Střední vzdělávání Typická věková skupina 17 – 19 let Datum vytvoření 16. 2. 2013

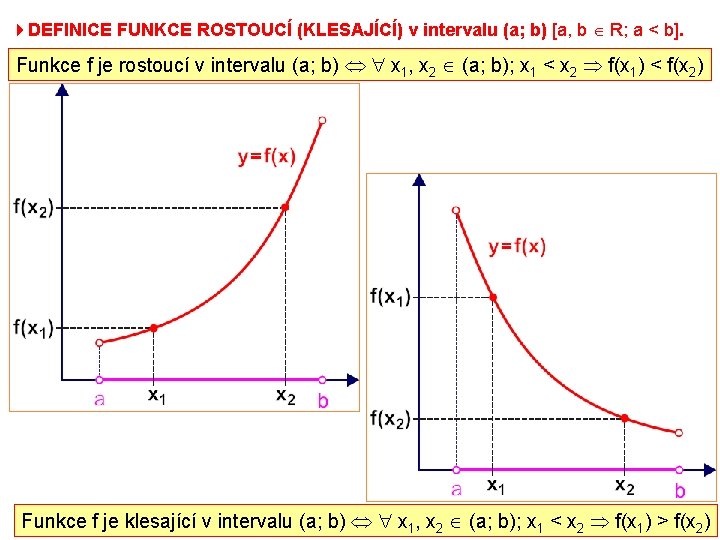
4 DEFINICE FUNKCE ROSTOUCÍ (KLESAJÍCÍ) v intervalu (a; b) [a, b R; a < b]. Funkce f je rostoucí v intervalu (a; b) x 1, x 2 (a; b); x 1 < x 2 f(x 1) < f(x 2) Funkce f je klesající v intervalu (a; b) x 1, x 2 (a; b); x 1 < x 2 f(x 1) > f(x 2)

4 ROLLEOVA VĚTA Předpokládejme, že funkce f(x) má následující vlastnosti: A) je spojitá v intervalu <a; b>, B) má derivaci (vlastní nebo nevlastní) v každém bodě otevřeného intervalu (a; b), C) f(a) = f(b). Potom existuje v otevřeném intervalu (a; b) alespoň jedno reálné číslo c, ve kterém platí f/(c) = 0. Geometrický význam Rolleovy věty

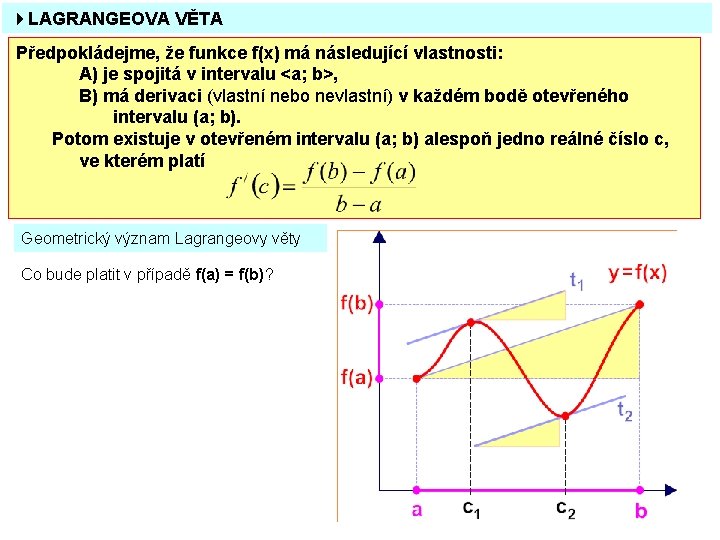
4 LAGRANGEOVA VĚTA Předpokládejme, že funkce f(x) má následující vlastnosti: A) je spojitá v intervalu <a; b>, B) má derivaci (vlastní nebo nevlastní) v každém bodě otevřeného intervalu (a; b). Potom existuje v otevřeném intervalu (a; b) alespoň jedno reálné číslo c, ve kterém platí Geometrický význam Lagrangeovy věty Co bude platit v případě f(a) = f(b)?

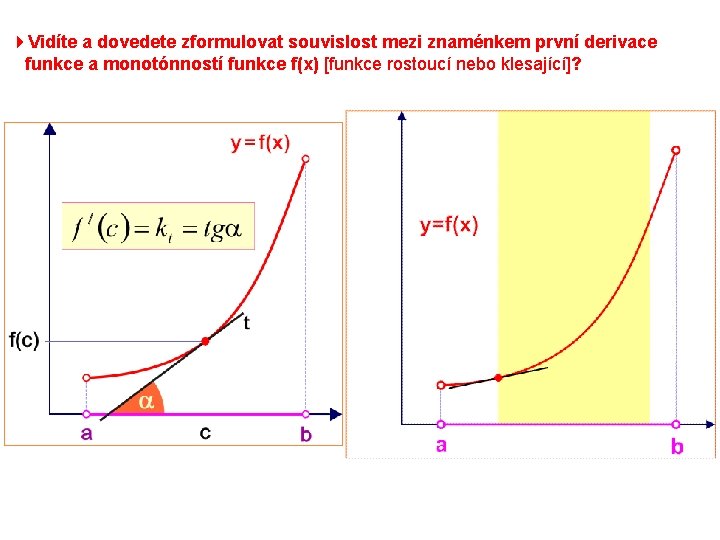
4 Vidíte a dovedete zformulovat souvislost mezi znaménkem první derivace funkce a monotónností funkce f(x) [funkce rostoucí nebo klesající]?

4 Vidíte a dovedete zformulovat souvislost mezi znaménkem první derivace funkce a monotónností funkce f(x) [funkce rostoucí nebo klesající]?

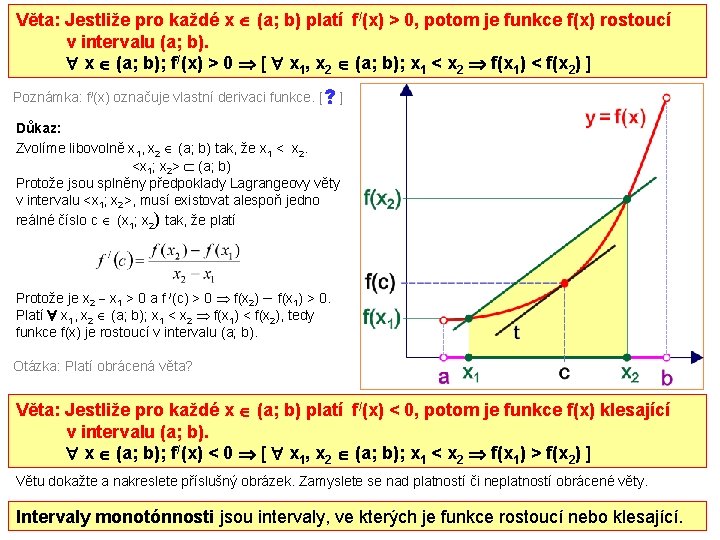
Věta: Jestliže pro každé x (a; b) platí f/(x) > 0, potom je funkce f(x) rostoucí v intervalu (a; b). x (a; b); f/(x) > 0 [ x 1, x 2 (a; b); x 1 < x 2 f(x 1) < f(x 2) ] Poznámka: f/(x) označuje vlastní derivaci funkce. [ ] Důkaz: Zvolíme libovolně x 1, x 2 (a; b) tak, že x 1 < x 2. <x 1; x 2> (a; b) Protože jsou splněny předpoklady Lagrangeovy věty v intervalu <x 1; x 2>, musí existovat alespoň jedno reálné číslo c (x 1; x 2) tak, že platí Protože je x 2 x 1 > 0 a f /(c) > 0 f(x 2) f(x 1) > 0. Platí x 1, x 2 (a; b); x 1 < x 2 f(x 1) < f(x 2), tedy funkce f(x) je rostoucí v intervalu (a; b). Otázka: Platí obrácená věta? Věta: Jestliže pro každé x (a; b) platí f/(x) < 0, potom je funkce f(x) klesající v intervalu (a; b). x (a; b); f/(x) < 0 [ x 1, x 2 (a; b); x 1 < x 2 f(x 1) > f(x 2) ] Větu dokažte a nakreslete příslušný obrázek. Zamyslete se nad platností či neplatností obrácené věty. Intervaly monotónnosti jsou intervaly, ve kterých je funkce rostoucí nebo klesající.

Věty používané při zjišťování monotónnosti funkce: Je-li f spojitá v intervalu <a; b> x (a; b); f / (x) > 0 funkce f je rostoucí v intervalu <a; b>. Je-li f spojitá v intervalu <a; b> x (a; b); f / (x) < 0 funkce f je klesající v intervalu <a; b>. 4 ILUSTRATIVNÍ PŘÍKLADY Určete intervaly monotónnosti funkce f: y = x 3 – 3 x 2 y/ = 3 x 2 – 6 x = 3 x. (x – 2) y/ > 0 3 x. (x – 2) > 0 Funkce f je rostoucí v intervalech (– ; 0>, < 2; + ). Funkce f je klesající v intervalu <0; 2>. Určete intervaly monotónnosti funkce f: y/ > 0 (x – 1). (x + 3). (x – 2) > 0 Funkce f je rostoucí v intervalech < – 3; 1>, <2; + ). Funkce f je klesající v intervalech (– ; – 3>, <1; 2>.

4 AUTOTEST Užitím derivace funkce určete intervaly, ve kterých je daná funkce rostoucí a ve kterých je klesající. p 1) y = 2 x 3 – x 2 – 8 x + 4 p 4) y = x 3 – 3 x 2 – 9 x p 2) y = – 2 x 3 + x 2 + 4 x + 3 p 5) y = 4 x 2 – x 4 p 3) y = 3 x 4 – 4 x 3 – 12 x 2 p 6) y = x 4 – 6 x 2 – 8 x – 3 MATEMATIKA – příprava k maturitě a k přijímacím zkouškám na vysoké školy, autor Jindra Petáková, vydalo nakladatelství Prometheus, spol. s r. o. , v roce 1998, strana 157, úloha 38. ISBN 80 -7196 -099 -3.

[ ] Věta: Jestliže má funkce f v bodě x 0 vlastní derivaci, potom je funkce v bodě x 0 spojitá. Důkaz: Podle definice spojitosti funkce v bodě x 0 máme dokázat, že Poznámka: Protože implikace (A B) a její obměna (( B) ( A)) mají stejnou pravdivostní hodnotu, musí platit také věta: Není-li funkce f spojitá v bodě x 0, potom funkce f nemá v bodě x 0 vlastní derivaci. To znamená, že derivace funkce f v bodě x 0 neexistuje nebo je nevlastní. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.