kola slo projektu Nzev projektu slo a nzev

Škola: Číslo projektu: Název projektu: Číslo a název šablony klíčové aktivity: Tematická oblast: Gymnázium Václava Hlavatého, Louny, Poděbradova 661, příspěvková organizace CZ. 1. 07/1. 5. 00/34. 0616 Inovace výuky EU-8 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Volitelný předmět matematika (matematický seminář) EU-8 -57 – DERIVACE FUNKCE XIII (globální i lokální extrémy funkce – úlohy na hledání extrémů) Anotace Globální extrémy funkce, jejich definice, hledání globálních extrémů funkce při řešení různých úloh (i slovních). Autor Paed. Dr. Milan Rieger Jazyk Čeština Očekávaný výstup Klíčová slova Druh učebního materiálu Druh interaktivity Cílová skupina Žák je schopen řešit jednoduché úlohy na vyhledávání globálních extrémů funkce. Globální maximum, globální minimum, slovní úloha, Weierstrassova věta. Pracovní list / Animace / Obrázky / Testy Aktivita / Výklad / Test / Kombinace Žák Stupeň a typ vzdělávání Střední vzdělávání Typická věková skupina 17 – 19 let Datum vytvoření 8. 12. 2013

4 DEFINICE GLOBÁLNÍHO MAXIMA Funkce f má na množině M D(f) globální maximum v bodě x 0 tehdy, když pro každé x M platí: f(x) f(x 0). 4 DEFINICE GLOBÁLNÍHO MINIMA Funkce f má na množině M D(f) globální minimum v bodě x 0 tehdy, když pro každé x M platí: f(x) f(x 0). 4 ZAJÍMAVÁ WEIERSTRASSOVA VĚTA Je-li funkce f spojitá v uzavřeném intervalu <a; b>, potom funkce f nabývá v intervalu <a; b> své největší a nejmenší hodnoty. To znamená, že 4 každá spojitá funkce v intervalu <a; b> má jistě globální extrémy; 4 existují čísla x 1, x 2 <a; b> taková, že pro všechna x <a; b> platí f(x 1) ≤ f(x 2); 4 každá spojitá funkce v intervalu <a; b> je omezená shora i zdola (oboustranně).

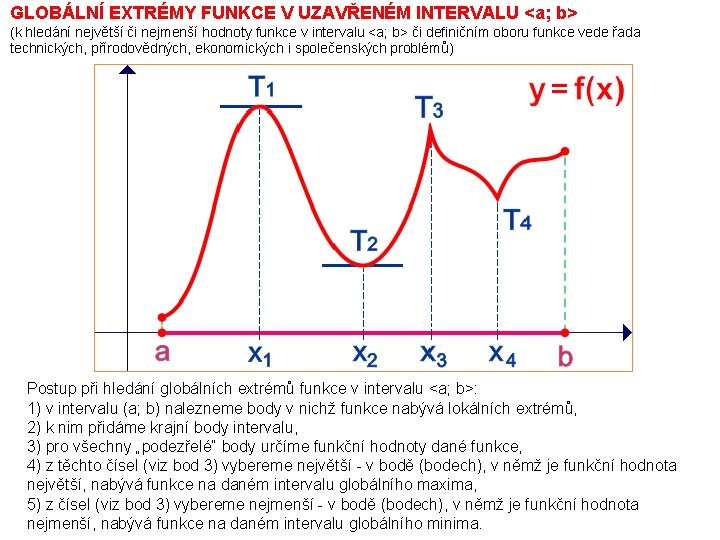
GLOBÁLNÍ EXTRÉMY FUNKCE V UZAVŘENÉM INTERVALU <a; b> (k hledání největší či nejmenší hodnoty funkce v intervalu <a; b> či definičním oboru funkce vede řada technických, přírodovědných, ekonomických i společenských problémů) Postup při hledání globálních extrémů funkce v intervalu <a; b>: 1) v intervalu (a; b) nalezneme body v nichž funkce nabývá lokálních extrémů, 2) k nim přidáme krajní body intervalu, 3) pro všechny „podezřelé“ body určíme funkční hodnoty dané funkce, 4) z těchto čísel (viz bod 3) vybereme největší - v bodě (bodech), v němž je funkční hodnota největší, nabývá funkce na daném intervalu globálního maxima, 5) z čísel (viz bod 3) vybereme nejmenší - v bodě (bodech), v němž je funkční hodnota nejmenší, nabývá funkce na daném intervalu globálního minima.

4 ILUSTRATIVNÍ ÚLOHA 1 Najděte absolutní extrémy funkce f: y = 2 x 3 – 6 x + 10 v intervalu <a; b> = < – 3; 3>. y/ = 6 x 2 – 6 y/ = 0 6 x 2 – 6 = 0 6 (x 2 – 1) = 0 6 (x – 1) (x + 1) = 0 (x = 1 x = – 1) body podezřelé z lokálních extrémů jsou – 1, 1 y// = 12 x y// (– 1) = – 12 funkce f má v bodě – 1 ostré lokální maximum; f(– 1) = 14 y// (1) = 12 funkce f má v bodě 1 ostré lokální minimum; f(1) = 6 Dále určíme hodnoty funkce f v krajních bodech intervalu <– 3; 3>. f(– 3) = – 26; f(3) = 46 Absolutní maximum funkce f v intervalu <– 3; 3> určíme výběrem největšího čísla z čísel 14; 6; – 26 a 46, což můžeme zapsat takto max (14; 6; – 26; 46) = 46 = f(3). Největší hodnoty (46) v intervalu <– 3; 3> nabývá funkce f v bodě 3. Absolutní minimum funkce f v intervalu <– 3; 3> určíme výběrem nejmenšího čísla z čísel 14; 6; – 26 a 46, což můžeme zapsat takto min (14; 6; – 26; 46) = – 26 = f(– 3). Nejmenší hodnoty (– 26) v intervalu <– 3; 3> nabývá funkce f v bodě – 3. 4ÚLOHA 1 (k samostatnému řešení) Najděte absolutní extrémy funkce f v intervalu <a; b> = < – 3; 2>. řešení úlohy

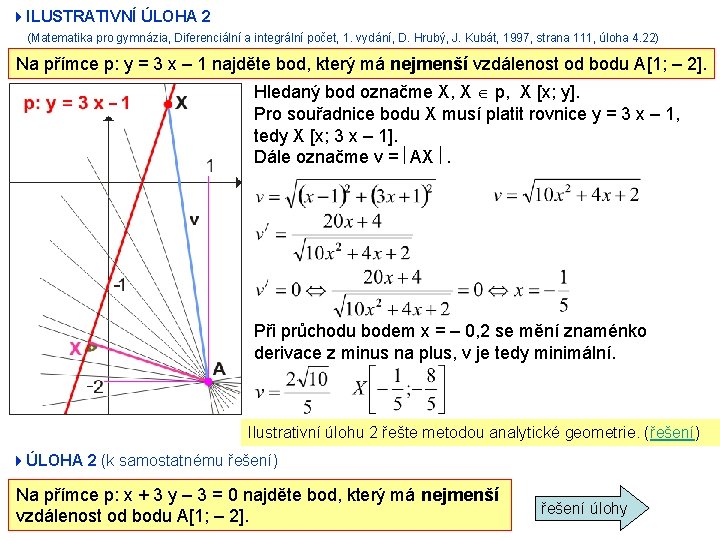
4 ILUSTRATIVNÍ ÚLOHA 2 (Matematika pro gymnázia, Diferenciální a integrální počet, 1. vydání, D. Hrubý, J. Kubát, 1997, strana 111, úloha 4. 22) Na přímce p: y = 3 x – 1 najděte bod, který má nejmenší vzdálenost od bodu A[1; – 2]. Hledaný bod označme X, X p, X [x; y]. Pro souřadnice bodu X musí platit rovnice y = 3 x – 1, tedy X [x; 3 x – 1]. Dále označme v = AX . Při průchodu bodem x = – 0, 2 se mění znaménko derivace z minus na plus, v je tedy minimální. Ilustrativní úlohu 2 řešte metodou analytické geometrie. (řešení) 4ÚLOHA 2 (k samostatnému řešení) Na přímce p: x + 3 y – 3 = 0 najděte bod, který má nejmenší vzdálenost od bodu A[1; – 2]. řešení úlohy

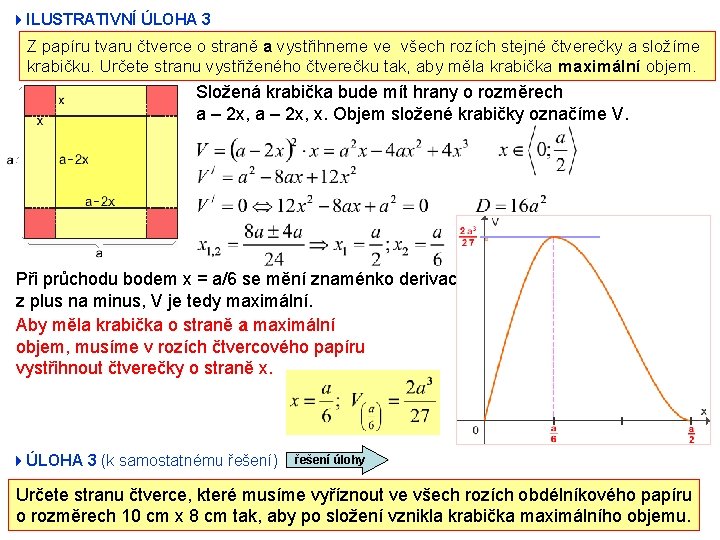
4 ILUSTRATIVNÍ ÚLOHA 3 Z papíru tvaru čtverce o straně a vystřihneme ve všech rozích stejné čtverečky a složíme krabičku. Určete stranu vystřiženého čtverečku tak, aby měla krabička maximální objem. Složená krabička bude mít hrany o rozměrech a – 2 x, x. Objem složené krabičky označíme V. Při průchodu bodem x = a/6 se mění znaménko derivace z plus na minus, V je tedy maximální. Aby měla krabička o straně a maximální objem, musíme v rozích čtvercového papíru vystřihnout čtverečky o straně x. 4ÚLOHA 3 (k samostatnému řešení) řešení úlohy Určete stranu čtverce, které musíme vyříznout ve všech rozích obdélníkového papíru o rozměrech 10 cm x 8 cm tak, aby po složení vznikla krabička maximálního objemu.

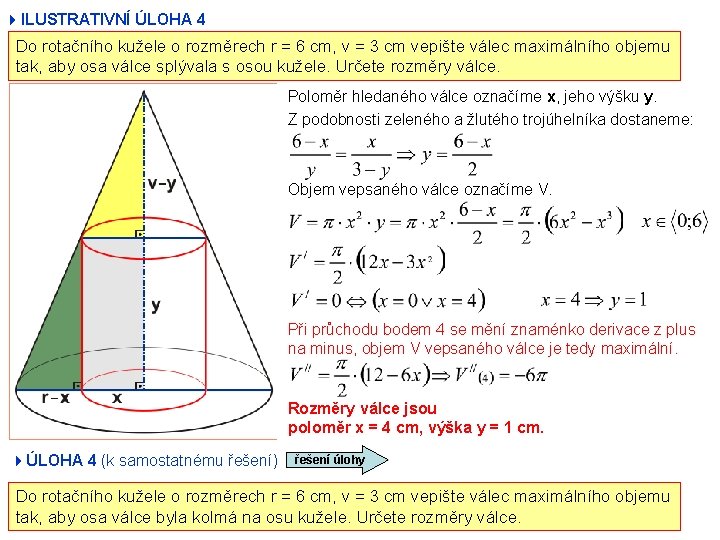
4 ILUSTRATIVNÍ ÚLOHA 4 Do rotačního kužele o rozměrech r = 6 cm, v = 3 cm vepište válec maximálního objemu tak, aby osa válce splývala s osou kužele. Určete rozměry válce. Poloměr hledaného válce označíme x, jeho výšku y. Z podobnosti zeleného a žlutého trojúhelníka dostaneme: Objem vepsaného válce označíme V. Při průchodu bodem 4 se mění znaménko derivace z plus na minus, objem V vepsaného válce je tedy maximální. Rozměry válce jsou poloměr x = 4 cm, výška y = 1 cm. 4ÚLOHA 4 (k samostatnému řešení) řešení úlohy Do rotačního kužele o rozměrech r = 6 cm, v = 3 cm vepište válec maximálního objemu tak, aby osa válce byla kolmá na osu kužele. Určete rozměry válce.

4ÚLOHY K PROCVIČENÍ 1. Určete rozměry válcové nádoby s víkem tak, aby při objemu 2 litry měla tato nádoba minimální povrch. 2. Určete rozměry válcové nádoby bez víka tak, aby při objemu 2 litry měla tato nádoba minimální povrch. 3. Do koule o poloměru 3 cm vepište válec maximálního objemu. Určete jeho rozměry. 4. Do koule o poloměru 3 cm vepište kužel maximálního objemu. Určete poloměr podstavy a výšku kužele. 5. Kouli o poloměru 3 cm opište kužel minimálního objemu. Určete jeho rozměry. 6. Určete rozměry obdélníku tak, aby při daném obsahu 16 cm 2 měl minimální obvod. 7. Určete rozměry obdélníku tak, aby při daném obvodu 20 cm měl maximální obsah. 8. Do ostroúhlého trojúhelníku ABC, c = 8 cm, vc = 4 cm vepište obdélník KLMN maximálního obsahu tak, aby KL AB. Určete jeho rozměry. MATEMATIKA PRO GYMNÁZIA – Diferenciální a integrální počet, 1. vydání, Dag Hrubý, Josef Kubát, 1997 vydalo nakladatelství Prometheus, spol. s r. o. , v roce 1997, strana 111, úloha 4. 22. ISBN 80 -7196 -063 -2. MATEMATIKA – příprava k maturitě a k přijímacím zkouškám na vysoké školy, autor Jindra Petáková, vydalo nakladatelství Prometheus, spol. s r. o. , v roce 1998, strana 161, úlohy 65, 66, 67, 68, 69, 70, 71, 73, 74, 75. ISBN 80 -7196 -099 -3. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.

4ÚLOHA 1 (řešení úlohy) Najděte absolutní extrémy funkce f v intervalu <a; b> = < – 3; 2>. y/ = x 2 + x – 2 y/ = 0 x 2 + x – 2 = 0 (x + 2) (x – 1) = 0 (x = 1 x = – 2) body podezřelé z lokálních extrémů jsou – 2, 1 y// = 2 x + 1 y// (– 2) = – 3 funkce f má v bodě – 2 ostré lokální maximum; f(– 2) = 22/3 y// (1) = 3 funkce f má v bodě 1 ostré lokální minimum; f(1) = 17/6 Dále určíme hodnoty funkce f v krajních bodech intervalu < – 3; 2>. f(– 3) = 11/2; f(2) = 14/3 max (22/3; 17/6; 11/2; 14/3) = 22/3 = f(– 2) Největší hodnoty (22/3) v intervalu <– 3; 2> nabývá funkce f v bodě – 2. min (22/3; 17/6; 11/2; 14/3) = 17/6 = f(1) Nejmenší hodnoty (17/6) v intervalu <– 3; 2> nabývá funkce f v bodě 1. návrat

4ÚLOHA 2 (řešení úlohy) Na přímce p: x + 3 y – 3 = 0 najděte bod, který má nejmenší vzdálenost od bodu A[1; – 2]. návrat Hledaný bod označme X, X p, X [x; y]. Pro souřadnice bodu X musí platit rovnice x + 3 y – 3 = 0, tedy Dále označme v = AX . Při průchodu bodem x = 1, 8 se mění znaménko derivace z minus na plus, v je tedy minimální.

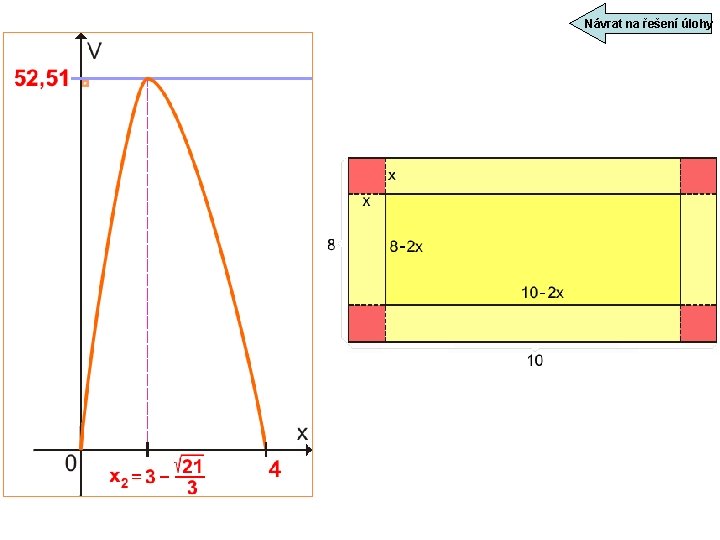
návrat 4ÚLOHA 3 (řešení úlohy) Určete stranu čtverce, které musíme vyříznout ve všech rozích obdélníkového papíru o rozměrech 10 cm x 8 cm tak, aby po složení vznikla krabička maximálního objemu. Při průchodu bodem x 2 se mění znaménko derivace z plus na minus, objem V krabičky je tedy maximální. graf

Návrat na řešení úlohy

návrat 4ÚLOHA 4 (řešení úlohy) Do rotačního kužele o rozměrech r = 6 cm, v = 3 cm vepište válec maximálního objemu tak, aby osa válce byla kolmá na osu kužele. Určete rozměry válce. Poloměr hledaného válce označíme r, jeho výšku v. Objem vepsaného válce označíme V. Z podobnosti zeleného a žlutého trojúhelníka dostaneme: Pro r = 1 cm a v = 4 cm je objem válce maximální, V = 4 .

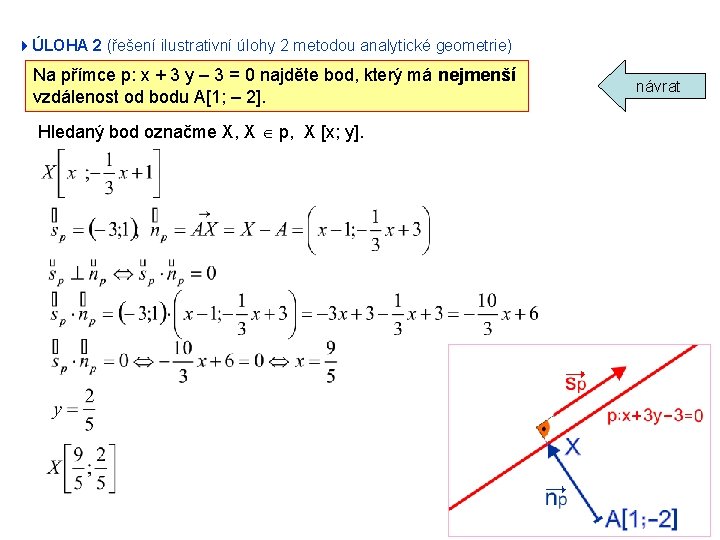
4ÚLOHA 2 (řešení ilustrativní úlohy 2 metodou analytické geometrie) Na přímce p: x + 3 y – 3 = 0 najděte bod, který má nejmenší vzdálenost od bodu A[1; – 2]. Hledaný bod označme X, X p, X [x; y]. návrat