kola slo projektu Nzev projektu slo a nzev

Škola: Číslo projektu: Název projektu: Číslo a název šablony klíčové aktivity: Tematická oblast: Gymnázium Václava Hlavatého, Louny, Poděbradova 661, příspěvková organizace CZ. 1. 07/1. 5. 00/34. 0616 Inovace výuky EU-8 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Volitelný předmět matematika (matematický seminář) EU-8 -56 – DERIVACE FUNKCE XII (lokální extrémy funkce – teorie, úlohy) Anotace Hledání lokálních extrémů pomocí první derivace funkce (monotónnosti funkce) a pomocí znaménka druhé derivace funkce. Obrázek jako prvek výuky vedoucí k pochopení pojmů, postupů a výpočtů. Autor Paed. Dr. Milan Rieger Jazyk Čeština Očekávaný výstup Klíčová slova Druh učebního materiálu Druh interaktivity Cílová skupina Žák je schopen určovat lokální extrémy jednoduchých funkcí dvěma způsoby, v případě možnosti je schopen zvolit efektivnější způsob výpočtu. Zjišťování extrémů funkce dovede žák využít při vyšetřování průběhu funkce. Žák chápe jednoduchou teorii a dovede ji konkrétně aplikovat. Lokální maximum, ostré lokální maximum, lokální minimum, ostré lokální minimum, první derivace funkce, funkce rostoucí, klesajícÍ. Stacionární bod, druhá derivace funkce, lokální extrém funkce. Pracovní list / Animace / Obrázky / Testy Aktivita / Výklad / Test / Kombinace Žák Stupeň a typ vzdělávání Střední vzdělávání Typická věková skupina 17 – 19 let Datum vytvoření 19. 11. 2013

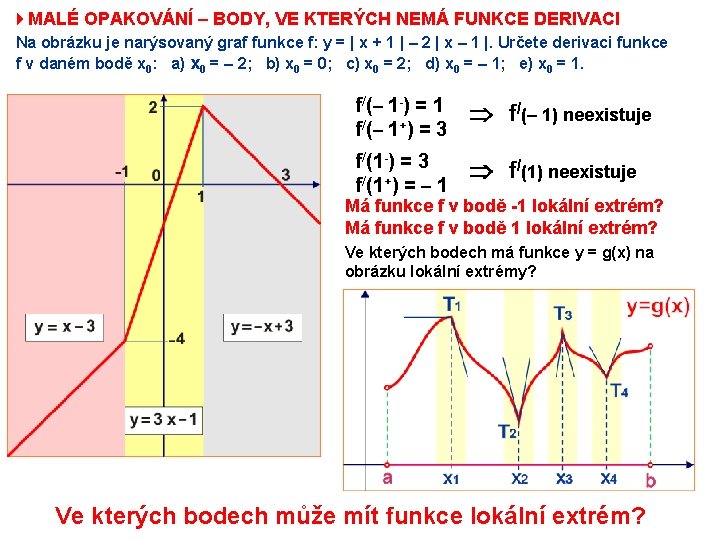
4 MALÉ OPAKOVÁNÍ – BODY, VE KTERÝCH NEMÁ FUNKCE DERIVACI Na obrázku je narýsovaný graf funkce f: y = | x + 1 | – 2 | x – 1 |. Určete derivaci funkce f v daném bodě x 0: a) x 0 = – 2; b) x 0 = 0; c) x 0 = 2; d) x 0 = – 1; e) x 0 = 1. f/(– 1 -) = 1 f/(– 1+) = 3 f/(– 1) neexistuje f/(1 -) = 3 f/(1+) = – 1 f/(1) neexistuje Má funkce f v bodě -1 lokální extrém? Má funkce f v bodě 1 lokální extrém? Ve kterých bodech má funkce y = g(x) na obrázku lokální extrémy? Ve kterých bodech může mít funkce lokální extrém?

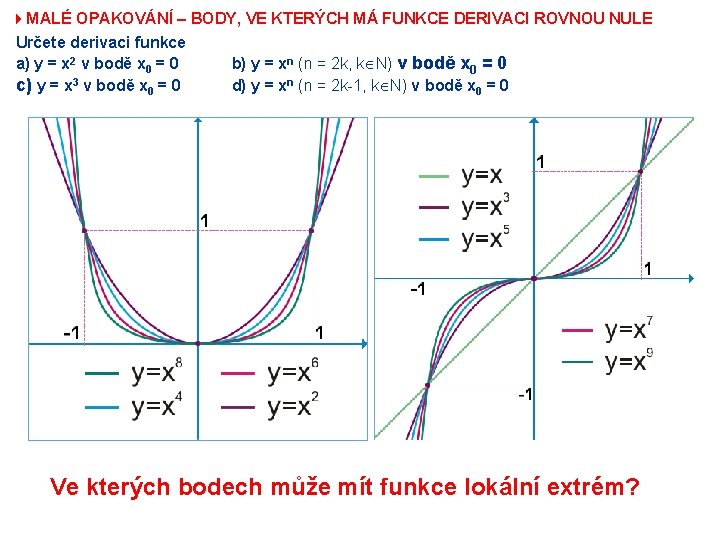
4 MALÉ OPAKOVÁNÍ – BODY, VE KTERÝCH MÁ FUNKCE DERIVACI ROVNOU NULE Určete derivaci funkce a) y = x 2 v bodě x 0 = 0 b) y = xn (n = 2 k, k N) v bodě x 0 = 0 c) y = x 3 v bodě x 0 = 0 d) y = xn (n = 2 k-1, k N) v bodě x 0 = 0 Ve kterých bodech může mít funkce lokální extrém?

Ve kterých bodech může mít funkce lokální extrém? Funkce může mít lokální extrémy v bodech, ve kterých je první derivace funkce rovna nule nebo neexistuje. Body, ve kterých je první derivace funkce rovna nule nebo neexistuje jsou body „podezřelé z extrémů“. Někdy se jim říká stacionární body. VĚTA (nutná, nikoliv však postačující podmínka existence lokálního extrému): Má-li funkce f v bodě x 0 lokální extrém a existuje-li v tomto bodě derivace f/(x 0), potom platí f/(x 0) = 0. 4 PROBLÉM K ŘEŠENÍ – formulujte větu obrácenou a rozhodněte, zda tato věta platí. Obrácená VĚTA: Je-li f/(x 0) = 0, potom má funkce f v bodě x 0 lokální extrém. Vzpomeňte si na některou mocninnou funkci s lichým přirozeným mocnitelem (např. f(x) = x 3) a hned se můžete k platnosti či neplatnosti této věty kvalifikovaně vyjádřit. f(x) = x 3 f/(x) = 3 x 2 funkce f má první derivaci rovnou nule v bodě x 0 = 0 (to je stacionární bod, tedy bod podezřelý z extrému), funkce f však v bodě x 0 = 0 nemá lokální extrém, protože je funkce f vlevo i vpravo od tohoto bodu rostoucí.

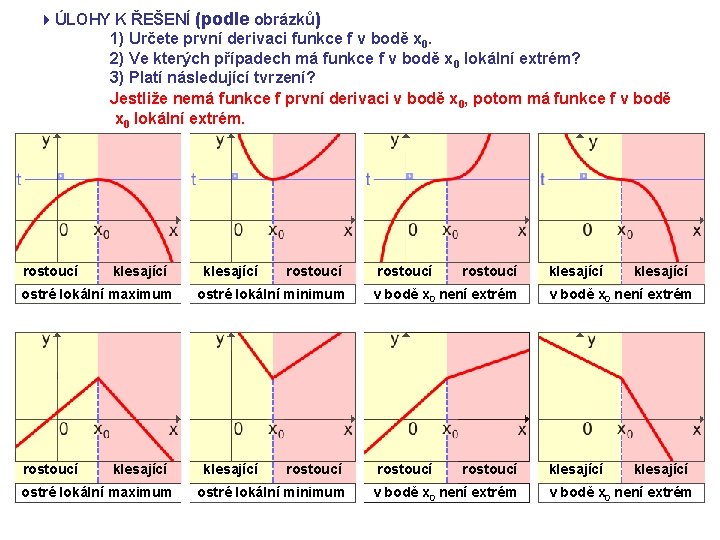
4ÚLOHY K ŘEŠENÍ (podle obrázků) 1) Určete první derivaci funkce f v bodě x 0. 2) Ve kterých případech má funkce f v bodě x 0 lokální extrém? 3) Platí následující tvrzení? Jestliže nemá funkce f první derivaci v bodě x 0, potom má funkce f v bodě x 0 lokální extrém. rostoucí klesající ostré lokální maximum klesající rostoucí ostré lokální minimum rostoucí v bodě x 0 není extrém klesající v bodě x 0 není extrém

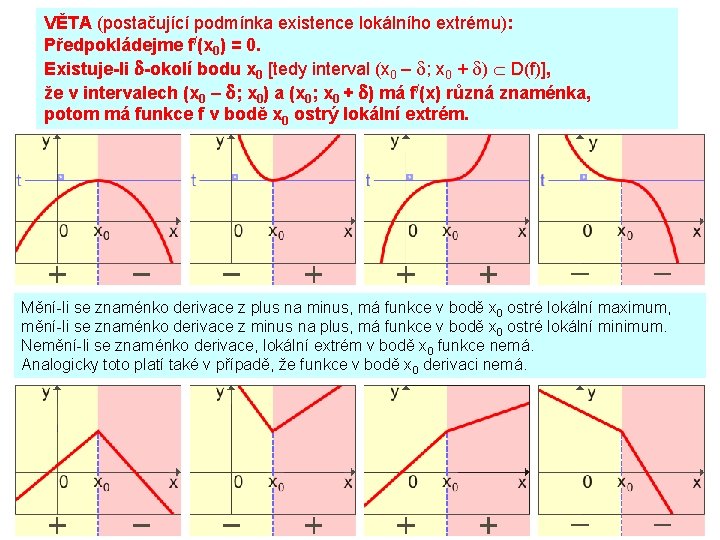
VĚTA (postačující podmínka existence lokálního extrému): Předpokládejme f/(x 0) = 0. Existuje-li d-okolí bodu x 0 [tedy interval (x 0 – d; x 0 + d) D(f)], že v intervalech (x 0 – d; x 0) a (x 0; x 0 + d) má f/(x) různá znaménka, potom má funkce f v bodě x 0 ostrý lokální extrém. Mění-li se znaménko derivace z plus na minus, má funkce v bodě x 0 ostré lokální maximum, mění-li se znaménko derivace z minus na plus, má funkce v bodě x 0 ostré lokální minimum. Nemění-li se znaménko derivace, lokální extrém v bodě x 0 funkce nemá. Analogicky toto platí také v případě, že funkce v bodě x 0 derivaci nemá.

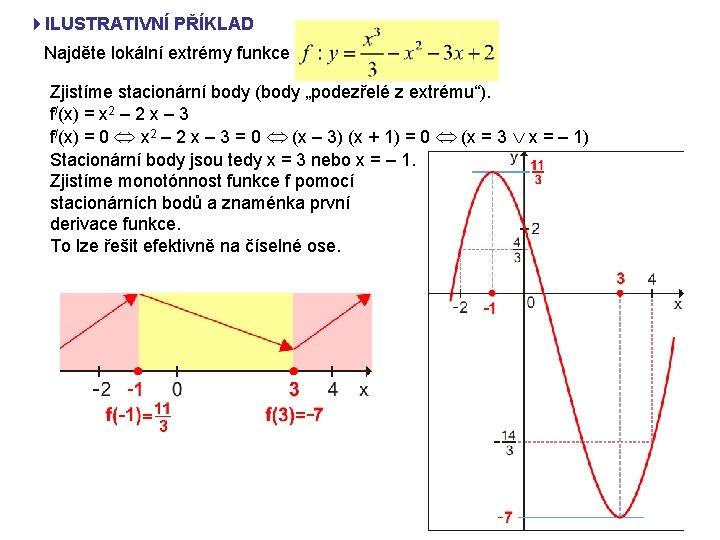
4 ILUSTRATIVNÍ PŘÍKLAD Najděte lokální extrémy funkce Zjistíme stacionární body (body „podezřelé z extrému“). f/(x) = x 2 – 2 x – 3 f/(x) = 0 x 2 – 2 x – 3 = 0 (x – 3) (x + 1) = 0 (x = 3 x = – 1) Stacionární body jsou tedy x = 3 nebo x = – 1. Zjistíme monotónnost funkce f pomocí stacionárních bodů a znaménka první derivace funkce. To lze řešit efektivně na číselné ose.

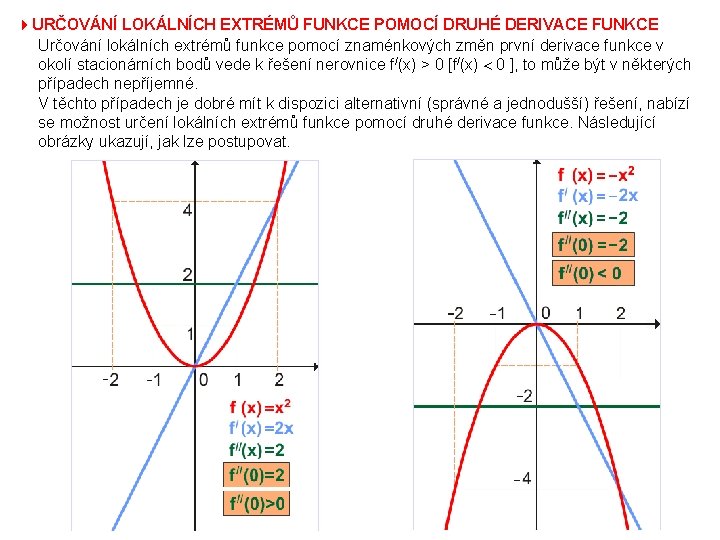
4 URČOVÁNÍ LOKÁLNÍCH EXTRÉMŮ FUNKCE POMOCÍ DRUHÉ DERIVACE FUNKCE Určování lokálních extrémů funkce pomocí znaménkových změn první derivace funkce v okolí stacionárních bodů vede k řešení nerovnice f/(x) > 0 [f/(x) 0 ], to může být v některých případech nepříjemné. V těchto případech je dobré mít k dispozici alternativní (správné a jednodušší) řešení, nabízí se možnost určení lokálních extrémů funkce pomocí druhé derivace funkce. Následující obrázky ukazují, jak lze postupovat.

VĚTA (postačující podmínka existence lokálního extrému pomocí druhé derivace funkce): Předpokládejme f/(x 0) = 0 a existenci druhé derivace funkce f v bodě x 0. Je-li f//(x 0) < 0, potom má funkce f v bodě x 0 ostré lokální maximum. Je-li f//(x 0) > 0, potom má funkce f v bodě x 0 ostré lokální minimum. Je-li f//(x 0) = 0, nelze podle uvedené věty rozhodnout o existenci lokálního extrému. Například pro funkci f(x) = x 4 platí: f/(x) = 4 x 3 bod podezřelý z extrému je x 0 = 0 f//(x) = 12 x 2 f//(x 0) = f//(0) = 0 podle uvedené věty o extrému funkce v bodě x 0 = 0 nelze rozhodnout Ze znalosti grafů mocninných funkcí však víme, že funkce f(x) = x 4 má v bodě x 0 = 0 ostré lokální minimum. Pokračujme ve výpočtů vyšších derivací … f///(x) = 24 x f///(x 0) = f///(0) = 0 f. IV(x) = 24 f. IV(x 0) = f. IV(0) = 24 f. IV(x 0) > 0 funkce f(x) = x 4 má v bodě x 0 ostré lokální minimum (uvedenou větu jsme mírně zobecnili). Zkuste si podobné mírné zobecnění také pro funkci f(x) = – x 6. VĚTA – zobecnění předcházející věty (postačující podmínka existence lokálního extrému pomocí znaménka sudé derivace funkce): Je dána funkce f, x 0 reálné číslo, n přirozené číslo. Je-li f/(x 0) = f///(x 0) = … = f(n-1)(x 0) = 0 a f(n)(x 0) 0, potom platí. Je-li n sudé a f(n)(x 0) > 0, potom má funkce f v bodě x 0 ostré lokální minimum. Je-li n sudé a f(n)(x 0) > 0, potom má funkce f v bodě x 0 ostré lokální maximum.

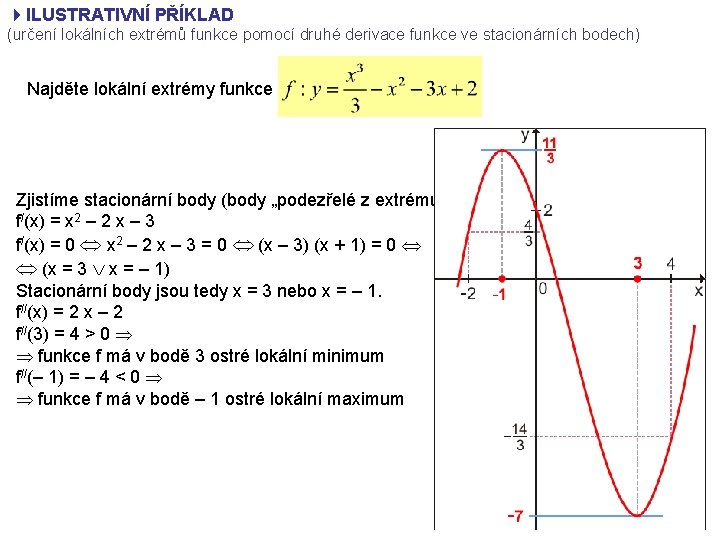
4 ILUSTRATIVNÍ PŘÍKLAD (určení lokálních extrémů funkce pomocí druhé derivace funkce ve stacionárních bodech) Najděte lokální extrémy funkce Zjistíme stacionární body (body „podezřelé z extrému“). f/(x) = x 2 – 2 x – 3 f/(x) = 0 x 2 – 2 x – 3 = 0 (x – 3) (x + 1) = 0 (x = 3 x = – 1) Stacionární body jsou tedy x = 3 nebo x = – 1. f//(x) = 2 x – 2 f//(3) = 4 > 0 funkce f má v bodě 3 ostré lokální minimum f//(– 1) = – 4 < 0 funkce f má v bodě – 1 ostré lokální maximum

4ÚLOHY K PROCVIČENÍ Určete lokální extrémy funkcí: MATEMATIKA – příprava k maturitě a k přijímacím zkouškám na vysoké školy, autor Jindra Petáková, vydalo nakladatelství Prometheus, spol. s r. o. , v roce 1998, strana 158, úloha 45. ISBN 80 -7196 -099 -3. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.

D(g 1)=R – { – 3} funkce g 1 má v bodě 0 ostré lokální minimum funkce g 1 má v bodě -6 ostré lokální maximum