kola slo projektu Nzev projektu slo a nzev

Škola: Číslo projektu: Název projektu: Číslo a název šablony klíčové aktivity: Tematická oblast: Gymnázium Václava Hlavatého, Louny, Poděbradova 661, příspěvková organizace CZ. 1. 07/1. 5. 00/34. 0616 Inovace výuky EU-8 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Volitelný předmět matematika (matematický seminář) EU-8 -47 – DERIVACE FUNKCE III (derivace elementárních funkcí) Anotace Odvození derivací elementárních funkcí pomocí definice derivace. Autor Paed. Dr. Milan Rieger Jazyk Čeština Očekávaný výstup Klíčová slova Druh učebního materiálu Druh interaktivity Cílová skupina Žák chápe odvození derivací elementárních funkcí pomocí definice derivace, zobecnění a zjednodušení zápisu první derivace funkce, umí derivovat jednoduché funkce zpaměti nebo zápisem postupu výpočtu derivace. Žák rozlišuje mezi derivací funkce v pevném bodě (x 0) a derivací funkce v libovolném bodě (x) definičního oboru funkce a umí odvozené vzorce aplikovat. Derivace funkce v bodě, derivace funkce v libovolném bodě definičního oboru funkce, „vzorce“ pro výpočet derivací elementárních funkcí. Pracovní list / Animace / Obrázky / Testy Aktivita / Výklad / Test / Kombinace Žák Stupeň a typ vzdělávání Střední vzdělávání Typická věková skupina 17 – 19 let Datum vytvoření 22. 12. 2012

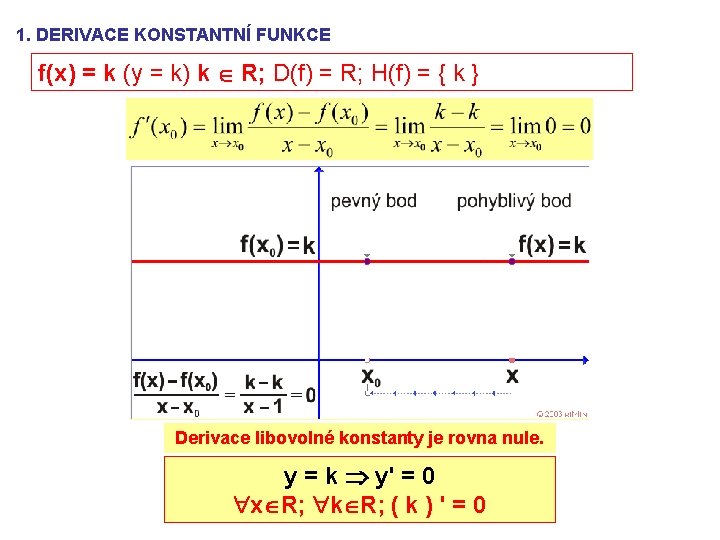
1. DERIVACE KONSTANTNÍ FUNKCE f(x) = k (y = k) k R; D(f) = R; H(f) = { k } Derivace libovolné konstanty je rovna nule. y = k y' = 0 x R; k R; ( k ) ' = 0

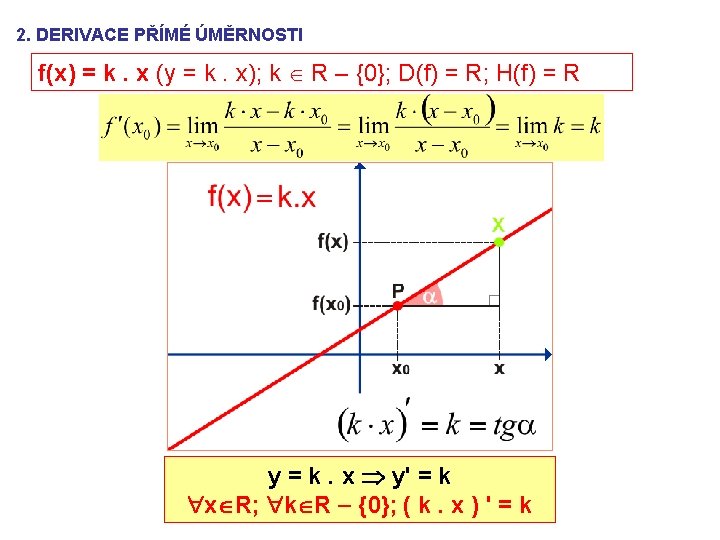
2. DERIVACE PŘÍMÉ ÚMĚRNOSTI f(x) = k. x (y = k. x); k R – {0}; D(f) = R; H(f) = R y = k. x y' = k x R; k R {0}; ( k. x ) ' = k

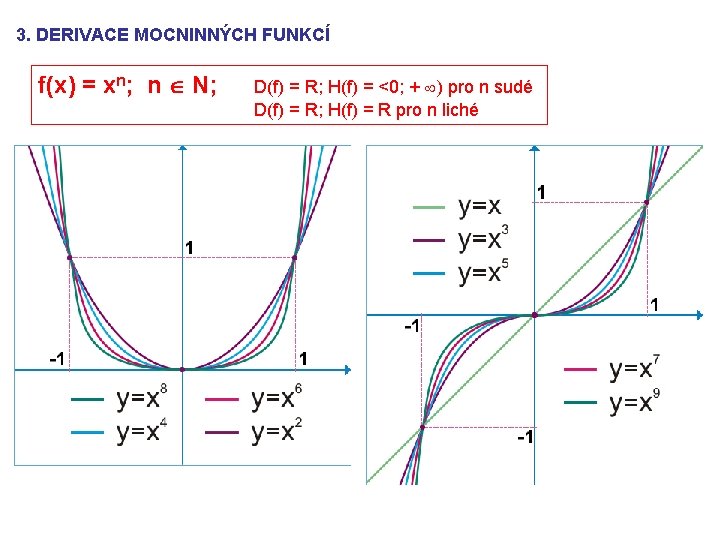
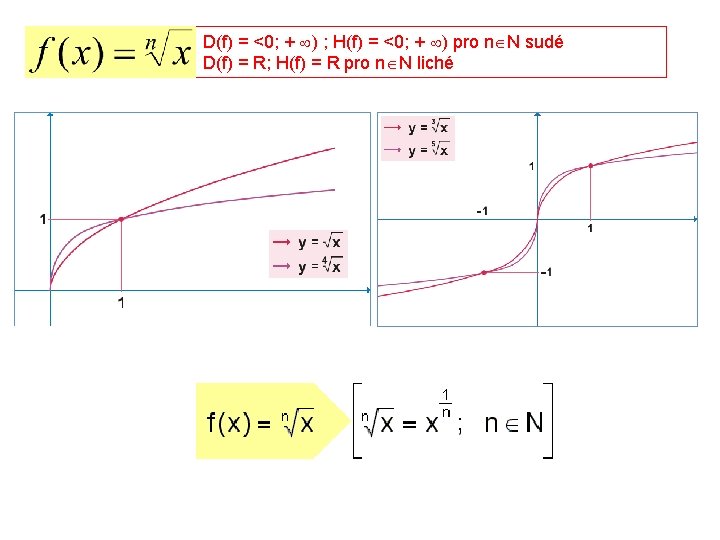
3. DERIVACE MOCNINNÝCH FUNKCÍ f(x) = xn; n N; D(f) = R; H(f) = <0; + ) pro n sudé D(f) = R; H(f) = R pro n liché

y = xn y' = n. xn– 1 x R; n N; ( xn ) ' = n. xn– 1 Počítejte zpaměti derivace v libovolném bodě definičního oboru dané funkce: a) y = x 3 b) y = x 8 c) y = x 23 d) y = x 112 Řešení úloh: a) y = 3 x 2 b) y = 8 x 7 c) y = 23 x 22 d) y = 112 x 111 Napište rovnice tečen a normál k dané funkci v bodě T[ 1; 1 ] (T[ - 1; ? ]): a) y = x 3 b) y = x 8 c) y = x 23 d) y = x 112 Řešení úloh: a) y'(1) = 3 t: 3 x – y – 2 = 0 n: x + 3 y – 4 = 0 b) y'(1) = 8 t: 8 x – y – 7 = 0 n: x + 8 y – 9 = 0 c) y'(1) = 23 t: 23 x – y – 22 = 0 n: x + 23 y – 24 = 0 d) y'(1) = 112 t: 112 x – y – 111 = 0 n: x + 112 y – 123 = 0

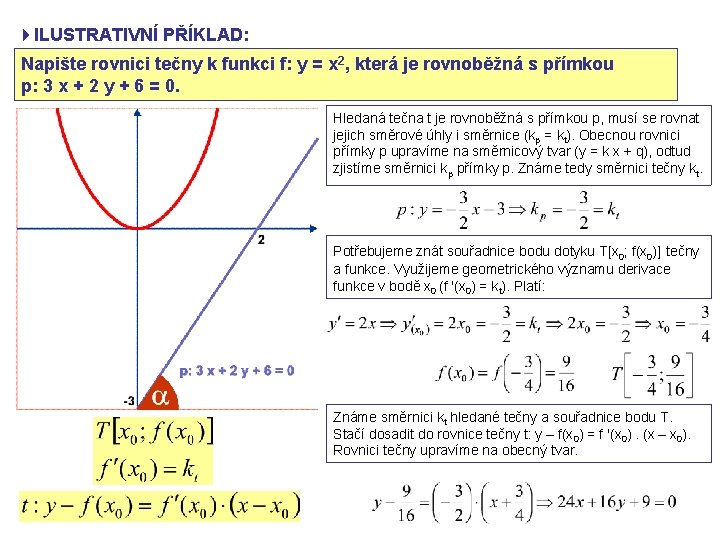
4 ILUSTRATIVNÍ PŘÍKLAD: Napište rovnici tečny k funkci f: y = x 2, která je rovnoběžná s přímkou p: 3 x + 2 y + 6 = 0. Hledaná tečna t je rovnoběžná s přímkou p, musí se rovnat jejich směrové úhly i směrnice (kp = kt). Obecnou rovnici přímky p upravíme na směrnicový tvar (y = k x + q), odtud zjistíme směrnici kp přímky p. Známe tedy směrnici tečny kt. Potřebujeme znát souřadnice bodu dotyku T[x 0; f(x 0)] tečny a funkce. Využijeme geometrického významu derivace funkce v bodě x 0 (f '(x 0) = kt). Platí: Známe směrnici kt hledané tečny a souřadnice bodu T. Stačí dosadit do rovnice tečny t: y – f(x 0) = f '(x 0). (x – x 0). Rovnici tečny upravíme na obecný tvar.

y = x- n y' = - n. x-n – 1 x R – { 0 }; n N; ( x-n ) ' = - n. x-n– 1 4 ILUSTRATIVNÍ PŘÍKLAD:

D(f) = <0; + ) ; H(f) = <0; + ) pro n N sudé D(f) = R; H(f) = R pro n N liché

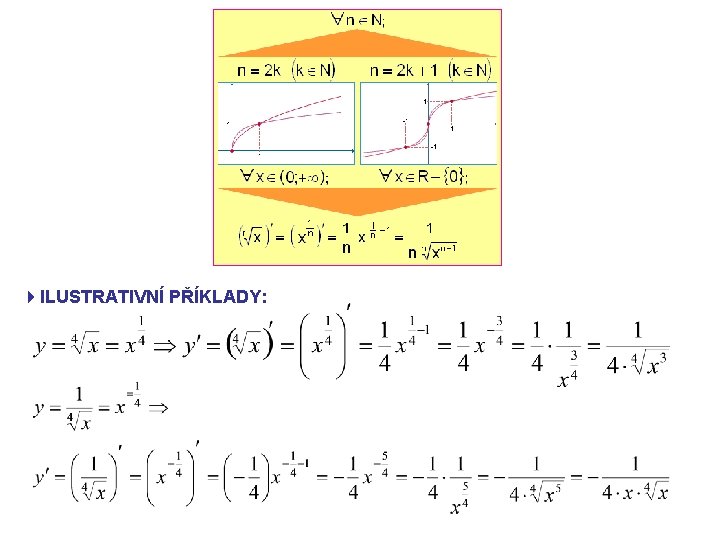
4 ILUSTRATIVNÍ PŘÍKLADY:

4. DERIVACE GONIOEMTRICKÝCH FUNKCÍ f(x) = sin x; D(f) = R; H(f) = < -1; 1 > f(x) = cos x; D(f) = R; H(f) = < -1; 1 >

AUTOTEST Napište rovnici tečny t a normály n k funkci f(x) v bodě T [x 0; f(x 0)]. Nakreslete graf funkce, zobrazte bod dotyku T, tečnu a normálu. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.

ŘEŠENÍ ÚLOH AUTOTESTU Úloha 1 Úloha 2 Úloha 3

ŘEŠENÍ ÚLOH AUTOTESTU Úloha 4 Úloha 5 Úloha 6

ŘEŠENÍ ÚLOH AUTOTESTU Úloha 7 Úloha 8 Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Milan Rieger.