Hyperbolic Geometry Chapter 9 Hyperbolic Lines and Segments

Hyperbolic Geometry Chapter 9

Hyperbolic Lines and Segments • Poincaré disk model § Line = circular arc, meets fundamental circle orthogonally • Note: § Lines closer to center of fundamental circle are closer to Euclidian lines § Why?

Poincaré Disk Model • Model of geometric world § Different set of rules apply • Rules § Points are interior to fundamental circle § Lines are circular arcs orthogonal to fundamental circle § Points where line meets fundamental circle are ideal points -- this set called • Can be thought of as “infinity” in this context

Poincaré Disk Model Euclid’s first four postulates hold 1. Given two distinct points, A and B, a unique line passing through them 2. Any line segment can be extended indefinitely § A segment has end points (closed) 3. Given two distinct points, A and B, a circle with radius AB can be drawn 4. Any two right angles are congruent

Hyperbolic Triangles • Recall Activity 2 – so … how do you find measure? • We find sum of angles might not be 180
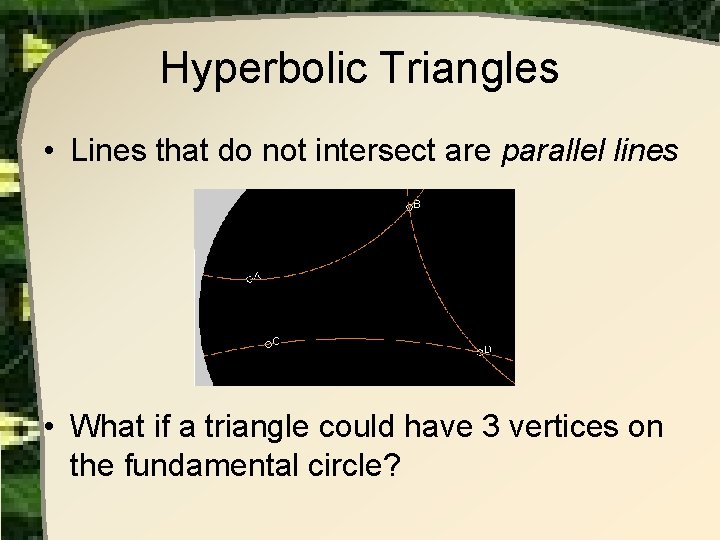
Hyperbolic Triangles • Lines that do not intersect are parallel lines • What if a triangle could have 3 vertices on the fundamental circle?

Hyperbolic Triangles • Note the angle measurements • What can you conclude when an angle is 0 ?

Hyperbolic Triangles • Generally the sum of the angles of a hyperbolic triangle is less than 180 • The difference between the calculated sum and 180 is called the defect of the triangle • Calculate the defect

Hyperbolic Polygons • What does the hyperbolic plane do to the sum of the measures of angles of polygons?

Hyperbolic Circles • A circle is the locus of points equidistant from a fixed point, the center What seems “wrong” with these results? • Recall Activity 9. 5

Hyperbolic Circles • What happens when the center or a point on the circle approaches “infinity”? • If center could be on fundamental circle § “Infinite” radius § Called a horocycle

Distance on Poincarè Disk Model • Rule for measuring distance metric • Euclidian distance Metric Axioms 1. d(A, B) = 0 A = B 2. d(A, B) = d(B, A) 3. Given A, B, C points, d(A, B) + d(B, C) d(A, C)

Distance on Poincarè Disk Model • Formula for distance M N § Where AM, AN, BM are Euclidian distances

Distance on Poincarè Disk Model Now work through axioms 1. d(A, B) = 0 A = B 2. d(A, B) = d(B, A) 3. Given A, B, C points, d(A, B) + d(B, C) d(A, C)

Circumcircles, Incircles of Hyperbolic Triangles • Consider Activity 9. 3 a § Concurrency of perpendicular bisectors

Circumcircles, Incircles of Hyperbolic Triangles • Consider Activity 9. 3 b § Circumcircle

Circumcircles, Incircles of Hyperbolic Triangles • Conjecture § Three perpendicular bisectors of sides of Poincarè disk are concurrent at O § Circle with center O, radius OA also contains points B and C

Circumcircles, Incircles of Hyperbolic Triangles • Note issue of bisectors sometimes not intersecting § More on this later …

Circumcircles, Incircles of Hyperbolic Triangles • Recall Activity 9. 4 § Concurrence of angle bisectors

Circumcircles, Incircles of Hyperbolic Triangles • Recall Activity 9. 4 § Resulting incenter

Circumcircles, Incircles of Hyperbolic Triangles • Conjecture § Three angle bisectors of sides of Poincarè disk are concurrent at O § Circle with center O, radius tangent to one side is tangent to all three sides

Congruence of Triangles in Hyperbolic Plane • Visual inspection unreliable • Must use axioms, theorems of hyperbolic plane § First four axioms are available • We will find that AAA is now a valid criterion for congruent triangles!!

Parallel Postulate in Poincaré Disk • Playfair’s Postulate l and any point P not on l, exactly one line on P that is parallel to l § Given any line P • Definition 9. 4 Two lines, l and m are parallel if the do not l intersect

Parallel Postulate in Poincaré Disk • Playfare’s postulate Says exactly one line through point P, parallel to line • What are two possible negations to the postulate? 1. No lines through P, parallel 2. Many lines through P, parallel Restate the first – Elliptic Parallel Postulate § There is a line l and a point P not on l such that every line through P intersects l

Elliptic Parallel Postulate • Examples of elliptic space § Spherical geometry • Great circle § “Straight” line on the sphere § Part of a circle with center at center of sphere
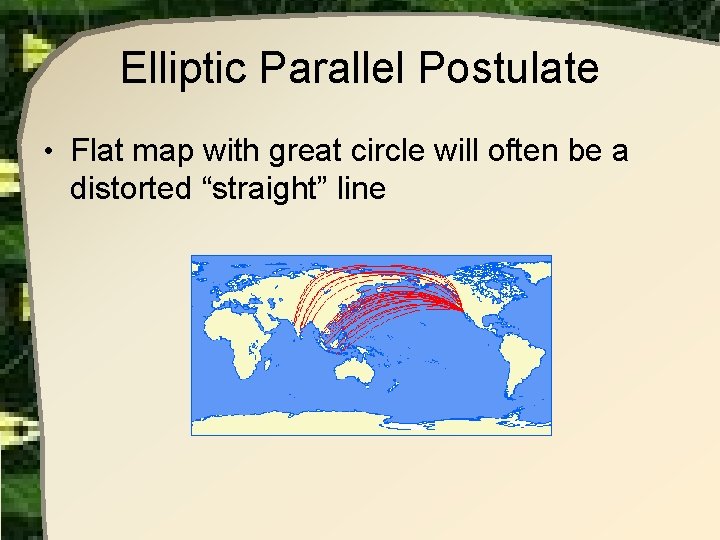
Elliptic Parallel Postulate • Flat map with great circle will often be a distorted “straight” line

Elliptic Parallel Postulate • Elliptic Parallel Theorem § Given any line l and a point P not on l every line through P intersects l • Let line l be the equator § All other lines (great circles) through any point must intersect the equator

Hyperbolic Parallel Postulate • Hyperbolic Parallel Postulate § There is a line l and a point P not on l such that … more than one line through P is parallel to l
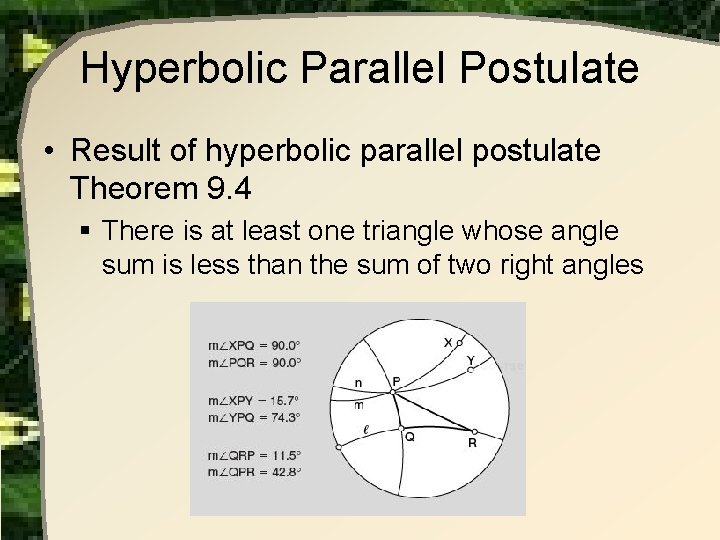
Hyperbolic Parallel Postulate • Result of hyperbolic parallel postulate Theorem 9. 4 § There is at least one triangle whose angle sum is less than the sum of two right angles
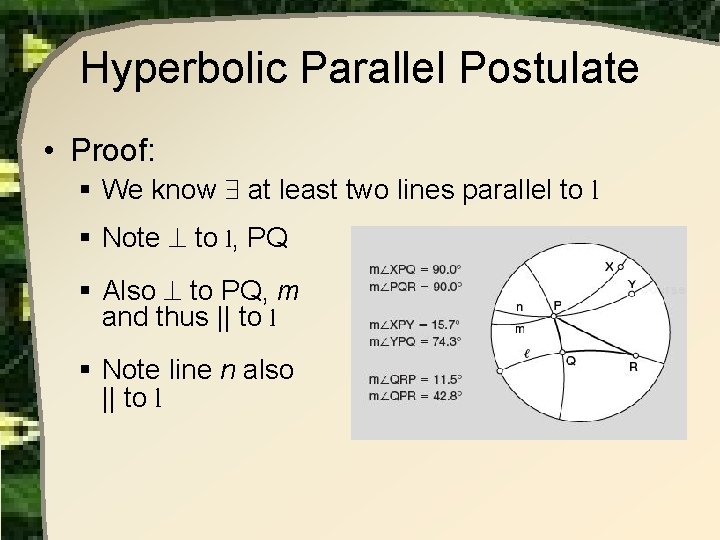
Hyperbolic Parallel Postulate • Proof: § We know at least two lines parallel to § Note to l, PQ § Also to PQ, m and thus || to l § Note line n also || to l l

Hyperbolic Parallel Postulate § XPY > 0 § Not R on l such that we have PQR § QPR < QPY § Move R towards fundamental circle, QRP 0 § Thus QRP < XPY § And PQR has one rt. angle and the other two sum < 90 § Thus sum of angles < 180

Parallel Lines, Hyperbolic Plane • Theorem 9. 5 Hyperbolic Parallel Theorem Given any line l, any point P, not on l, at leas two lines through P, parallel to l § Remember parallel means they don’t intersect

Parallel Lines, Hyperbolic Plane • Lines outside the limiting rays will be parallel to line AB § Called ultraparallel or superparallel or hyperparallel § Note line ED is limiting parallel with D at
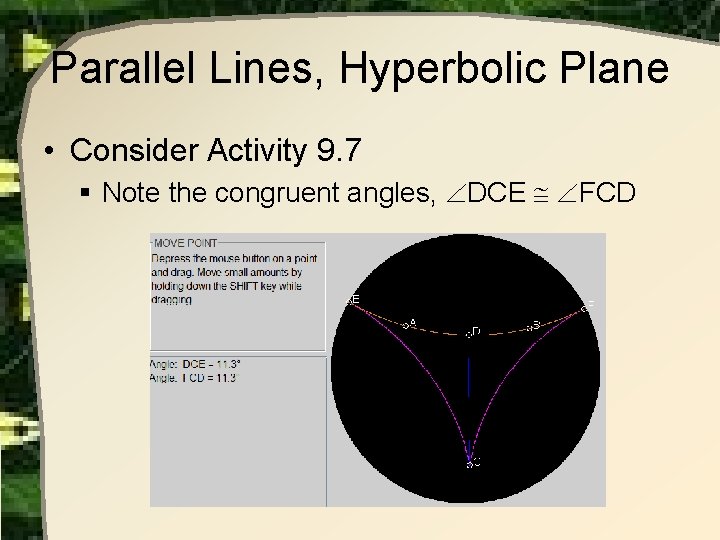
Parallel Lines, Hyperbolic Plane • Consider Activity 9. 7 § Note the congruent angles, DCE FCD
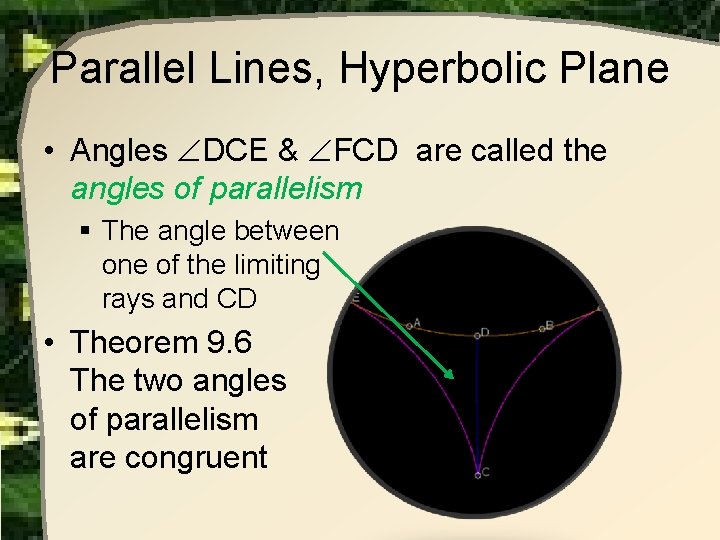
Parallel Lines, Hyperbolic Plane • Angles DCE & FCD are called the angles of parallelism § The angle between one of the limiting rays and CD • Theorem 9. 6 The two angles of parallelism are congruent
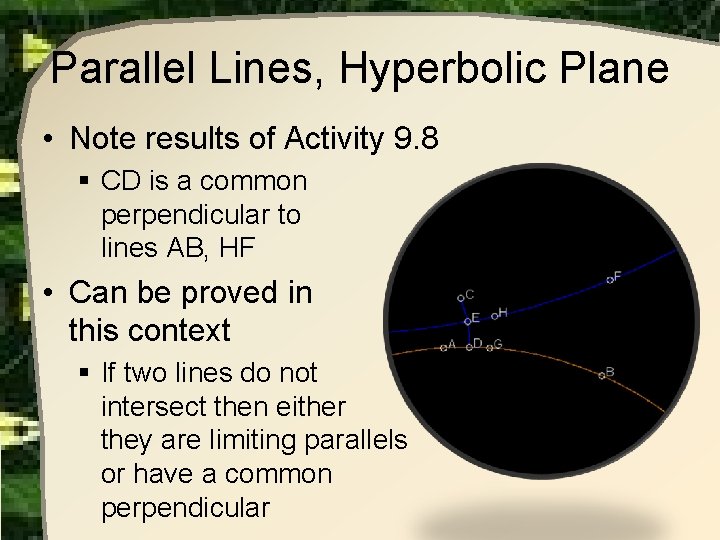
Parallel Lines, Hyperbolic Plane • Note results of Activity 9. 8 § CD is a common perpendicular to lines AB, HF • Can be proved in this context § If two lines do not intersect then either they are limiting parallels or have a common perpendicular

Quadrilaterals, Hyperbolic Plane • Recall results of Activity 9. 9 • 90 angles at B and A

Quadrilaterals, Hyperbolic Plane • Recall results of Activity 9. 10 • 90 angles at B, A, and D only • Called a Lambert quadrilateral

Quadrilaterals, Hyperbolic Plane • Saccheri quadrilateral § A pair of congruent sides § Both perpendicular to a third side

Quadrilaterals, Hyperbolic Plane • Angles at A and B are base angles • Angles at E and F are summit angles § Note they are congruent • Side EF is the summit • You should have found not possible to construct rectangle (4 right angles)

Hyperbolic Geometry Chapter 9
- Slides: 41