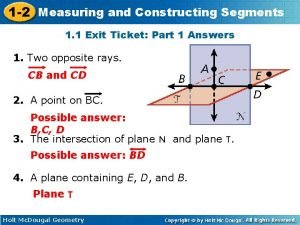
1 2 Measuring and Constructing Segments Section 1





















- Slides: 23

1 -2 Measuring and Constructing Segments Section 1. 2 Measuring and Constructing Segments Holt Geometry

1 -2 Measuring and Constructing Segments Objectives Use length and midpoint of a segment. Construct midpoints and congruent segments. Holt Geometry

1 -2 Measuring and Constructing Segments A ruler can be used to measure the distance between two points. A point corresponds to one and only one number on a ruler. The number is called a ______. The following postulate summarizes this concept. Holt Geometry

1 -2 Measuring and Constructing Segments The _____ between any two points is the absolute value of the difference of the coordinates. If the coordinates of points A and B are a and b, then the distance between A and B is |a – b| or |b – a|. The distance between A and B is also called the ______ of AB, or AB. A a Holt Geometry B b AB = _____ or _____

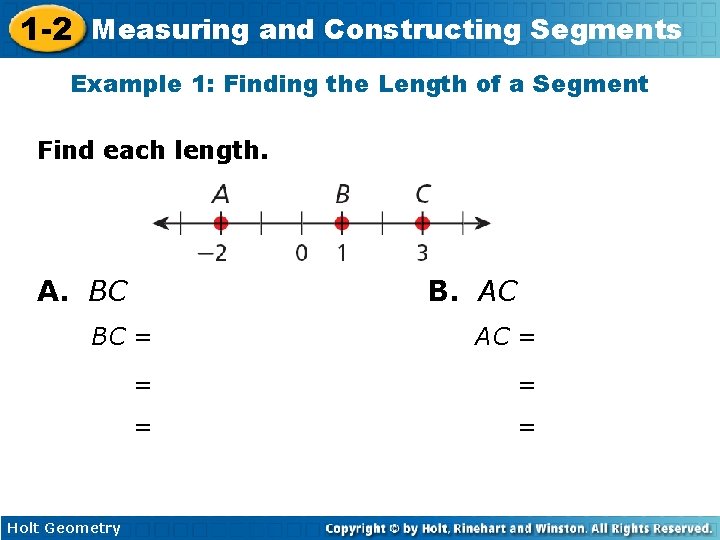
1 -2 Measuring and Constructing Segments Example 1: Finding the Length of a Segment Find each length. A. BC B. AC BC = AC = = = Holt Geometry

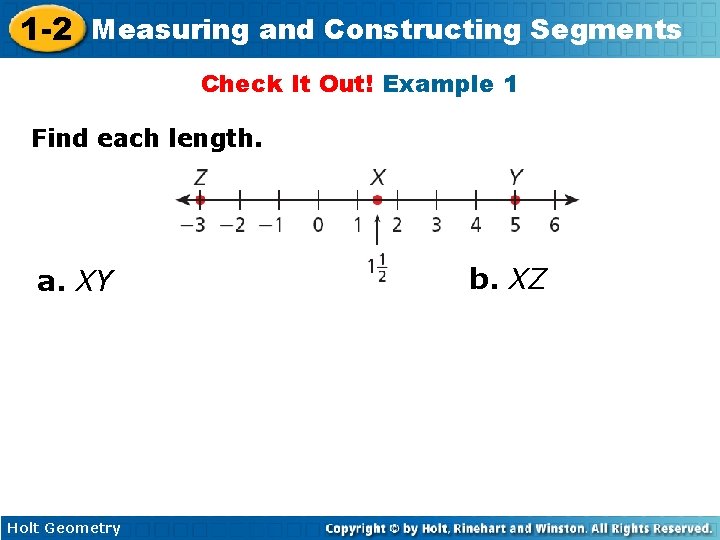
1 -2 Measuring and Constructing Segments Check It Out! Example 1 Find each length. a. XY Holt Geometry b. XZ

1 -2 Measuring and Constructing Segments _________ are segments that have the same length. In the diagram, PQ = RS, so you can write PQ RS. This is read as “segment PQ is congruent to segment RS. ” Tick marks are used in a figure to show congruent segments. Holt Geometry

1 -2 Measuring and Constructing Segments In order for you to say that a point B is ____ two points A and C, all three points must lie on the same line, and AB + BC = AC. Holt Geometry

1 -2 Measuring and Constructing Segments Example 2 A: Using the Segment Addition Postulate G is between F and H, FG = 6, and FH = 11. Find GH. FH = FG + GH Holt Geometry Seg. Add. Postulate Substitute 6 for FG and 11 for FH. Subtract 6 from both sides. Simplify.

1 -2 Measuring and Constructing Segments Example 2 B: Using the Segment Addition Postulate M is between N and O. Find NO. NM + MO = NO Seg. Add. Postulate Substitute the given values Simplify. Subtract 2 from both sides. Simplify. Subtract 3 x from both sides. Divide both sides by 2. Holt Geometry

1 -2 Measuring and Constructing Segments Example 2 B Continued M is between N and O. Find NO. NO = 5 x + 2 Substitute 5 for x. Simplify. Holt Geometry

1 -2 Measuring and Constructing Segments Check It Out! Example 3 a Y is between X and Z, XZ = 3, and XY = . Find YZ. XZ = XY + YZ Seg. Add. Postulate Substitute the given values. Subtract Holt Geometry from both sides.

1 -2 Measuring and Constructing Segments Check It Out! Example 3 b E is between D and F. Find DF. DE + EF = DF Seg. Add. Postulate Substitute the given values Subtract 3 x from both sides. Simplify. Divide both sides by 3. Holt Geometry

1 -2 Measuring and Constructing Segments Check It Out! Example 3 b Continued E is between D and F. Find DF. DF = 6 x Substitute 4 for x. Simplify. Holt Geometry

1 -2 Measuring and Constructing Segments The ____M of AB is the point that _______, or divides, the segment into two congruent segments. If M is the midpoint of AB, then AM = MB. So if AB = ___, then AM = ___ and MB = ___ Holt Geometry

1 -2 Measuring and Constructing Segments Example 4: Recreation Application The map shows the route for a race. You are at X, 6000 ft from the first checkpoint C. The second checkpoint D is located at the midpoint between C and the end of the race Y. The total race is 3 miles. How far apart are the 2 checkpoints? XY = = Holt Geometry Convert race distance to feet.

1 -2 Measuring and Constructing Segments Example 4 Continued XC + CY = XY Seg. Add. Post. Substitute 6000 for XC and 15, 840 for XY. Subtract 6000 from both sides. Simplify. D is the mdpt. of CY, so CD = CY. The checkpoints are ____ft apart. Holt Geometry

1 -2 Measuring and Constructing Segments Check It Out! Example 4 You are 365 m from the first-aid station. What is the distance to a drink station located at the midpoint between your current location and the first-aid station? Holt Geometry

1 -2 Measuring and Constructing Segments Example 5: Using Midpoints to Find Lengths D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 4 x + 6 Step 1 Solve for x. ED = DF Holt Geometry D 7 x – 9 F

1 -2 Measuring and Constructing Segments Example 5 Continued D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E Holt Geometry 4 x + 6 D 7 x – 9 F

1 -2 Measuring and Constructing Segments Example 5 Continued D is the midpoint of EF, ED = 4 x + 6, and DF = 7 x – 9. Find ED, DF, and EF. E 4 x + 6 D 7 x – 9 F Step 2 Find ED, DF, and EF. ED = 4 x + 6 Holt Geometry DF = 7 x – 9 EF = ED + DF

1 -2 Measuring and Constructing Segments Check It Out! Example 5 S is the midpoint of RT, RS = – 2 x, and ST = – 3 x – 2. Find RS, ST, and RT. R – 2 x Step 1 Solve for x. Holt Geometry S – 3 x – 2 T

1 -2 Measuring and Constructing Segments Check It Out! Example 5 Continued S is the midpoint of RT, RS = – 2 x, and ST = – 3 x – 2. Find RS, ST, and RT. R – 2 x S – 3 x – 2 T Step 2 Find RS, ST, and RT. RS = – 2 x Holt Geometry ST = – 3 x – 2 RT = RS + ST
 1-3 measuring and constructing angles
1-3 measuring and constructing angles Measuring and constructing segments
Measuring and constructing segments Measuring and constructing segments
Measuring and constructing segments 1-2 measuring and constructing segments lesson quiz answers
1-2 measuring and constructing segments lesson quiz answers Chapter 1 measuring and constructing segments
Chapter 1 measuring and constructing segments Measuring and constructing segments
Measuring and constructing segments Lesson 1-2 measuring and constructing segments
Lesson 1-2 measuring and constructing segments Measuring and constructing segments
Measuring and constructing segments 1-2 measuring and constructing segments
1-2 measuring and constructing segments Measuring and constructing angles
Measuring and constructing angles Measuring and constructing angles worksheet
Measuring and constructing angles worksheet Find reference angle
Find reference angle Practice 11-3 inscribed angles answer key
Practice 11-3 inscribed angles answer key Angles objectives
Angles objectives Measuring and constructing angles
Measuring and constructing angles 1-3 measuring and constructing angles
1-3 measuring and constructing angles 1-1 lesson quiz measuring segments and angles
1-1 lesson quiz measuring segments and angles Measuring segments and angles
Measuring segments and angles Straight angle
Straight angle Measuring segments quick check
Measuring segments quick check Measuring segments
Measuring segments Measuring line segments
Measuring line segments Measuring segments worksheet
Measuring segments worksheet Postulate 1-1
Postulate 1-1