Warmup 1 2 1 2 Points Lines and



















- Slides: 31

Warm-up 1. 2

1. 2 Points, Lines and Planes 1. 3 Segments, Rays, Parallel Lines Geometry Gonzales

Definitions • Think of points as locations. – Points have no defined size or shape – Represented by a small dot – Named by a capital letter. • Space: – Defined as the set of all points 3

Definitions • Line – Series of points that extends in two opposite directions without end • Collinear points – Points that lie on the same line • Plane – Flat surface – No specified thickness – Contains many lies and extends without end in the directions of all its lines. • Coplanar – Points and lines that lie in the same plane. 4

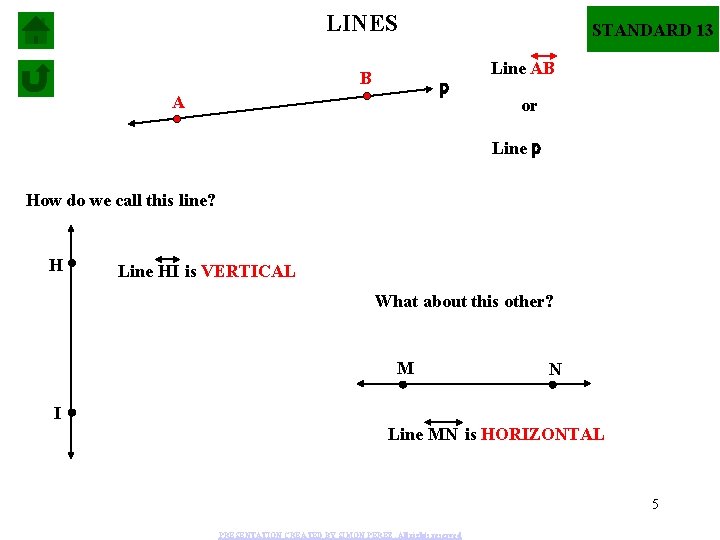
LINES B STANDARD 13 p A Line AB or Line p How do we call this line? H Line HI is VERTICAL What about this other? M N I Line MN is HORIZONTAL 5 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

LINES C D E F STANDARD 13 m How many different ways can we call Line m? Line DC Line CD Line CE OR Line CF Line EC Line FC Line DE Line DF Can you figure out other names? Line EF IN GENERAL A LINE IS NAMED BY TWO POINTS. PRESENTATION CREATED BY SIMON PEREZ. All rights reserved 6

Definitions • Postulate (axiom) – Accepted statement of fact • Segment – Is part of a line consisting of two endpoints and all points between them. • Ray – Part of a line consisting of one endpoint and all the points of the line on one side of the endpoint. • Opposite Rays – Two collinear rays with the same endpoint 7

Definitions • Parallel Lines – Coplanar lines that do not intersect • Skew Lines – Noncoplanar • Not parallel and do not intersect • Parallel planes – Planes that do not intersect 8

SEGMENTS STANDARD 13 If we have line DE and we take one part of the line D E 9 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

SEGMENTS STANDARD 13 If we have line DE and we take one part of the line D E then this part is called: LINE SEGMENT DE Can you name the different line segments in the following line: S SEGMENTS: T U TS ST SU TU OR US UT 10 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

RAYS STANDARD 13 B This is RAY AB A What are the differences between a Line, a Line Segment and a Ray? The line is infinite and never ends at either side. D The line segment has two endpoints. M N E The ray has on one side one endpoint at the other side it never ends it goes on to infinite. A B What do they have in common? They are named using TWO POINTS. 11 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

COLLINEAR VS NONCOLLINEAR STANDARD 13 Points C, D, E and F: are they COLLINEAR? D C F E Yes, they are COLLINEAR because they lie in the same line Are points A, B, C, and D collinear? C A B D No, they are NONCOLLINEAR because they don’t lie in the same line. 12 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

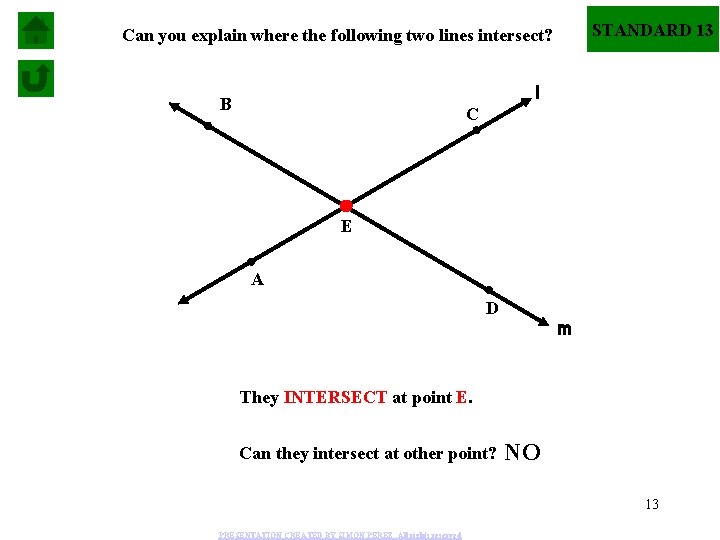
STANDARD 13 Can you explain where the following two lines intersect? l B C E A D m They INTERSECT at point E. Can they intersect at other point? NO 13 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

STANDARD 13 PLANES A B D M This is: PLANE M PLANE ADC C PLANE BDC PLANE ABD In general a Plane can be named using three non-collinear points. The figure above represents a PLANE, which is a flat surface that has no end at any of the sides. What examples can you give of objects lying in a PLANE? • The wall of a house • The lid of a shoebox. • The ground of a football field. PRESENTATION CREATED BY SIMON PEREZ. All rights reserved 14

Postulates • 1 -1 – Through any two points there is exactly one line. • 1 -2 – If two lines intersect, then they intersect in exactly one point. • 1 -3 – If two planes intersect, then they intersect in exactly one line. • 1 -4 – Through any three noncollinear points there is exactly one plane. 15

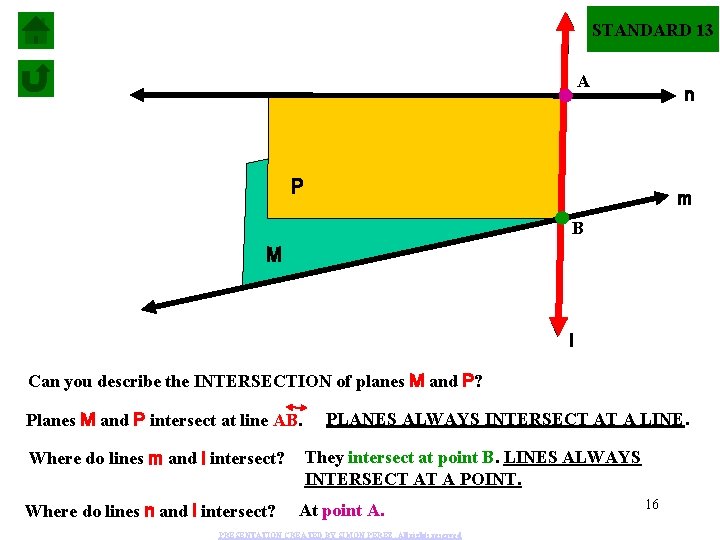
STANDARD 13 A n P m B M l Can you describe the INTERSECTION of planes M and P? Planes M and P intersect at line AB. Where do lines m and l intersect? Where do lines n and l intersect? PLANES ALWAYS INTERSECT AT A LINE. They intersect at point B. LINES ALWAYS INTERSECT AT A POINT. At point A. PRESENTATION CREATED BY SIMON PEREZ. All rights reserved 16

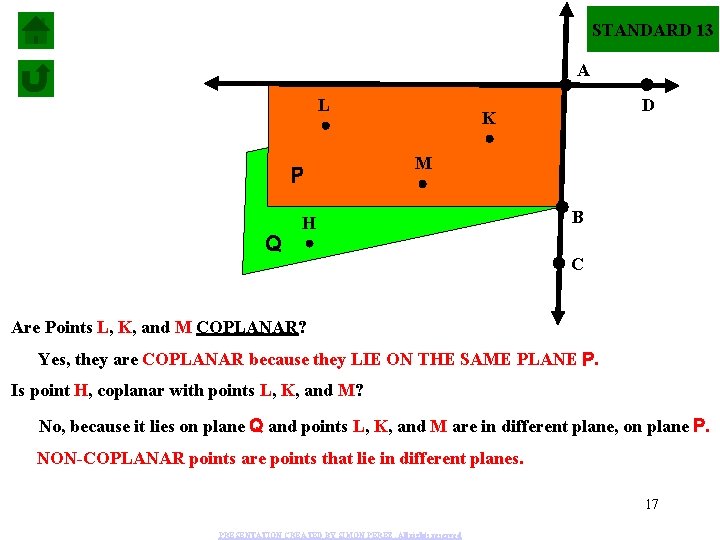
STANDARD 13 A L P Q D K M H B C Are Points L, K, and M COPLANAR? Yes, they are COPLANAR because they LIE ON THE SAME PLANE P. Is point H, coplanar with points L, K, and M? No, because it lies on plane Q and points L, K, and M are in different plane, on plane P. NON-COPLANAR points are points that lie in different planes. 17 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

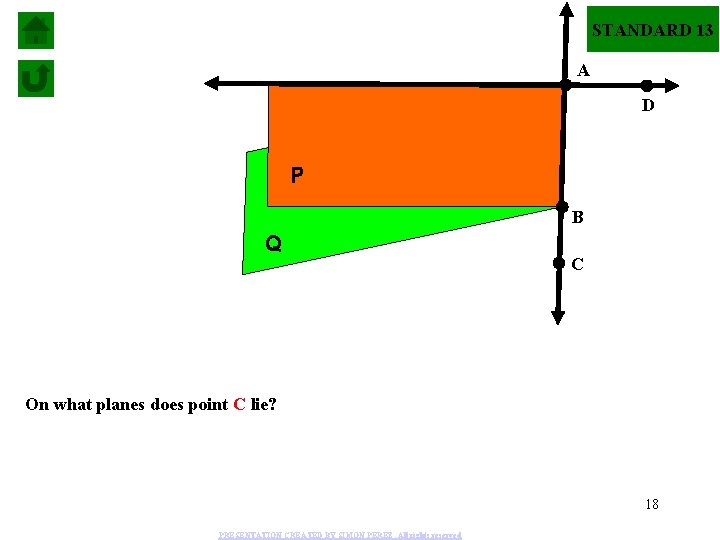
STANDARD 13 A D P B Q C On what planes does point C lie? 18 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

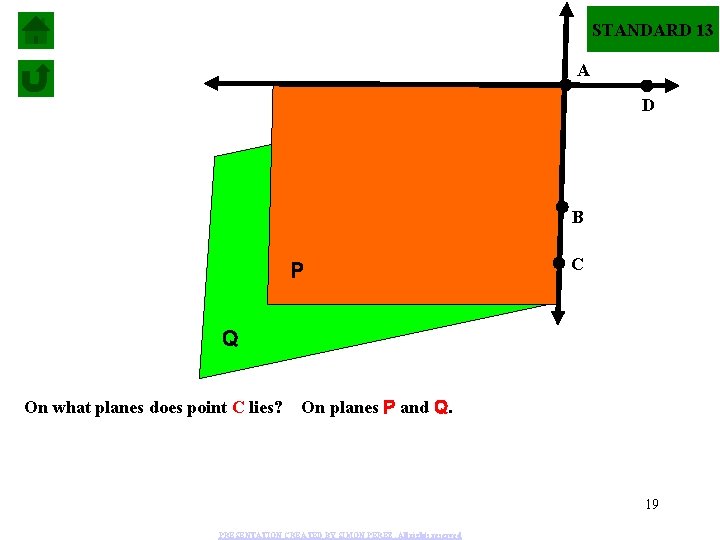
STANDARD 13 A D B P C Q On what planes does point C lies? On planes P and Q. 19 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

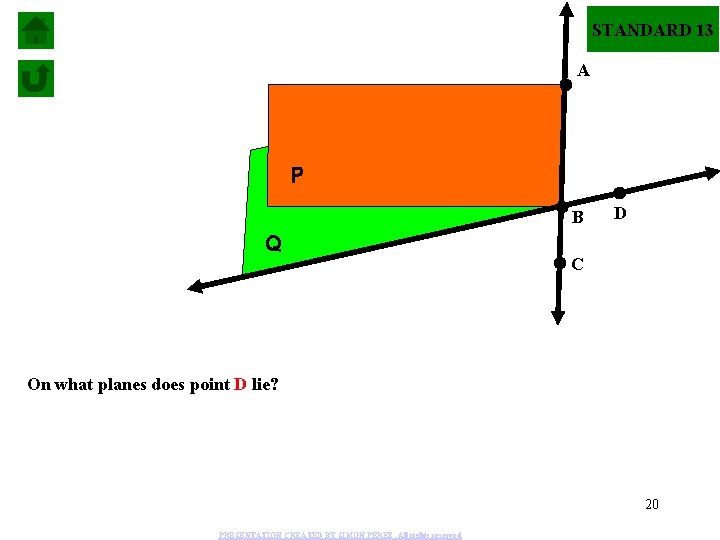
STANDARD 13 A P B Q D C On what planes does point D lie? 20 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

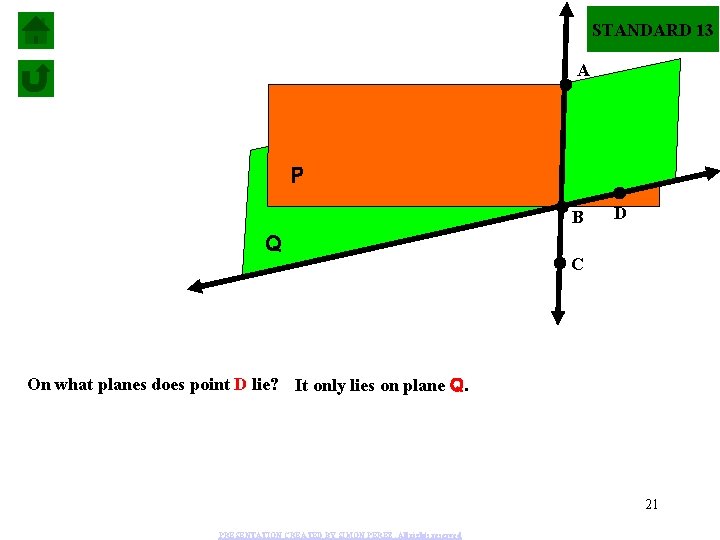
STANDARD 13 A P B Q D C On what planes does point D lie? It only lies on plane Q. 21 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

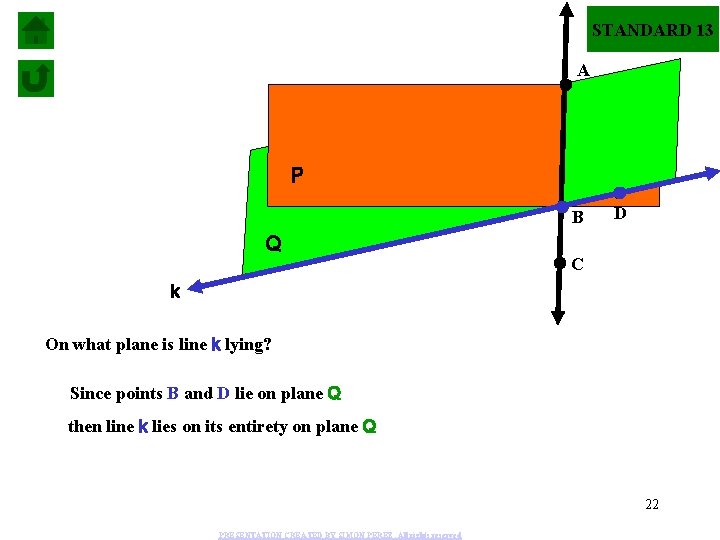
STANDARD 13 A P B Q D C k On what plane is line k lying? Since points B and D lie on plane Q then line k lies on its entirety on plane Q 22 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

STANDARD 13 SUMMARIZING FINDINGS: • Through any two points there is exactly one line. • Through any three points not on the same line there is exactly one plane or through any three points non-collinear there is one plane. • A line contains at least two points. • A plane contains at least three points not on the same line. • A plane contains at least three non-collinear points. • If two points lie in a plane, the entire line containing those points lies in that plane. 23 PRESENTATION CREATED BY SIMON PEREZ. All rights reserved

Points, Lines, and Planes LESSON 1 -3 Additional Examples In the figure below, name three points that are collinear and three points that are not collinear. Points Y, Z, and W lie on a line, so they are collinear. Any other set of three points do not lie on a line, so no other set of three points is collinear. For example, X, Y, and Z and X, W, and Z form triangles and are not collinear. Quick Check 24

Points, Lines, and Planes LESSON 1 -3 Additional Examples Name the plane shown in two different ways. You can name a plane using any three or more points on that plane that are not collinear. Some possible names for the plane shown are the following: plane RST plane RSU plane RTU plane STU plane RSTU Quick Check 25

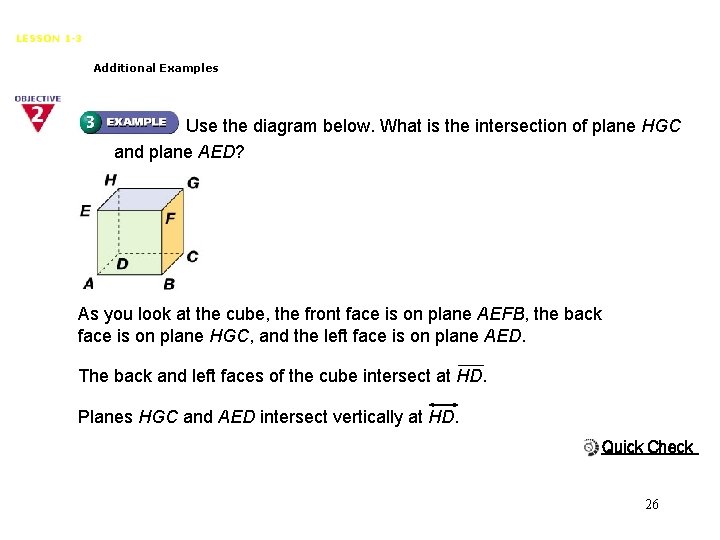
Points, Lines, and Planes LESSON 1 -3 Additional Examples Use the diagram below. What is the intersection of plane HGC and plane AED? As you look at the cube, the front face is on plane AEFB, the back face is on plane HGC, and the left face is on plane AED. The back and left faces of the cube intersect at HD. Planes HGC and AED intersect vertically at HD. Quick Check 26

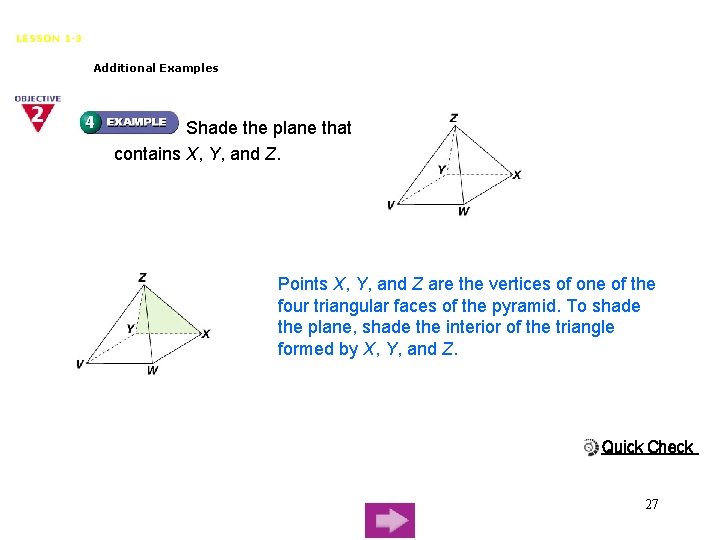
Points, Lines, and Planes LESSON 1 -3 Additional Examples Shade the plane that contains X, Y, and Z. Points X, Y, and Z are the vertices of one of the four triangular faces of the pyramid. To shade the plane, shade the interior of the triangle formed by X, Y, and Z. Quick Check 27

Segments, Rays, Parallel Lines and Planes LESSON 1 -4 Additional Examples Name the segments and rays in the figure. The labeled points in the figure are A, B, and C. A segment is a part of a line consisting of two endpoints and all points between them. A segment is named by its two endpoints. So the segments are BA (or AB) and BC (or CB). A ray is a part of a line consisting of one endpoint and all the points of the line on one side of that endpoint. A ray is named by its endpoint first, followed by any other point on the ray. So the rays are BA and BC. Quick Check 28

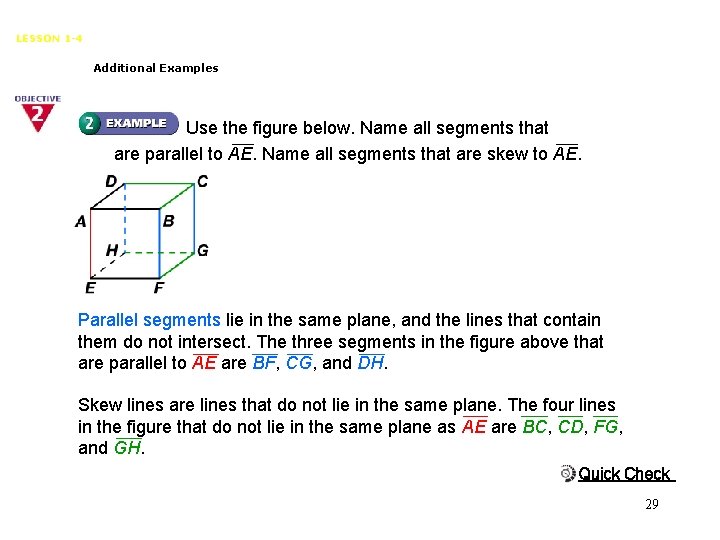
Segments, Rays, Parallel Lines and Planes LESSON 1 -4 Additional Examples Use the figure below. Name all segments that are parallel to AE. Name all segments that are skew to AE. Parallel segments lie in the same plane, and the lines that contain them do not intersect. The three segments in the figure above that are parallel to AE are BF, CG, and DH. Skew lines are lines that do not lie in the same plane. The four lines in the figure that do not lie in the same plane as AE are BC, CD, FG, and GH. Quick Check 29

Segments, Rays, Parallel Lines and Planes LESSON 1 -4 Additional Examples Identify a pair of parallel planes in your classroom. Planes are parallel if they do not intersect. If the walls of your classroom are vertical, opposite walls are parts of parallel planes. If the ceiling and floor of the classroom are level, they are parts of parallel planes. Quick Check 30

Assignment • 1. 2 – Pg. 14 38 -80 even; 90 -96 • 1. 3 – Pg. 19 5 -7; 11 -18; 37 -47 31