Lesson 1 2 Segments and Rays Postulates Definition








- Slides: 12

Lesson 1 -2 Segments and Rays

Postulates Definition: an assumption that needs no explanation. Examples: • Through any two points there is exactly one line. • A line contains at least two points. • Through any three points, there is exactly one plane. • A plane contains at least three points.

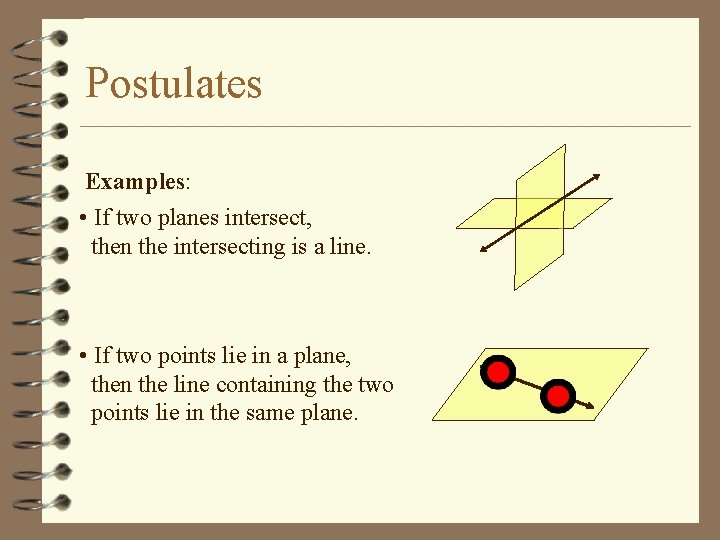
Postulates Examples: • If two planes intersect, then the intersecting is a line. • If two points lie in a plane, then the line containing the two points lie in the same plane.

Postulates The Ruler Postulate: The points on any line can be paired with the real numbers in such a way that: • Any two chosen points can be paired with 0 and 1. • The distance between any two points in a number line is the absolute value of the difference of the real numbers corresponding to the points. | | PK = 3 - -2 = 5 (distance is always positive)

Between Definition: X is between A and B if AX + XB = AB AX + XB > AB

Segment Definition: two endpoints and all points between How to sketch: How to name:

The Segment Addition Postulate (This is the same as “between. ” ) Postulate: If C is between A and B, then AC + CB = AB. Example: If AC = x , CB = 2 x and AB = 12, then Find x, AC and CB. 2 x x AC + CB = AB x + 2 x = 12 3 x = 12 x = 4 AC = 4 CB = 8

Congruent Segments Definition: segments with equal lengths ~ ) ( the symbol for congruent is = Congruent segments can be marked with. . . Numbers are equal. Objects are congruent. AB: the distance from A to B ( a number ) AB: the segment AB ( an object ) Correct notation: Incorrect notation:

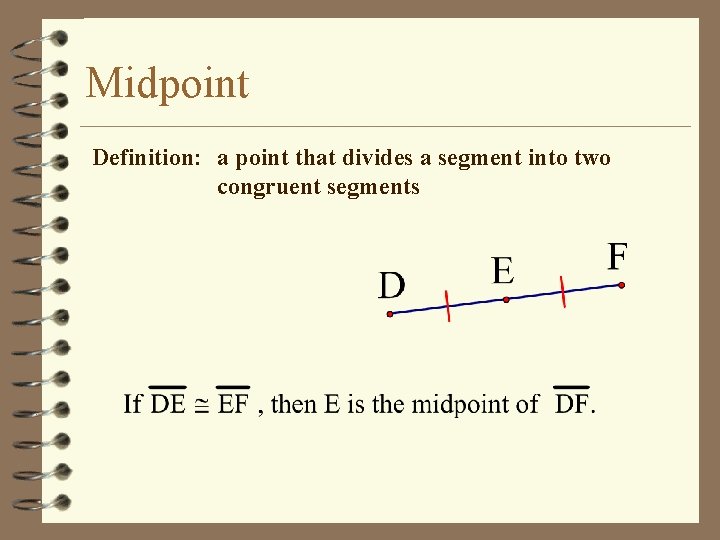
Midpoint Definition: a point that divides a segment into two congruent segments

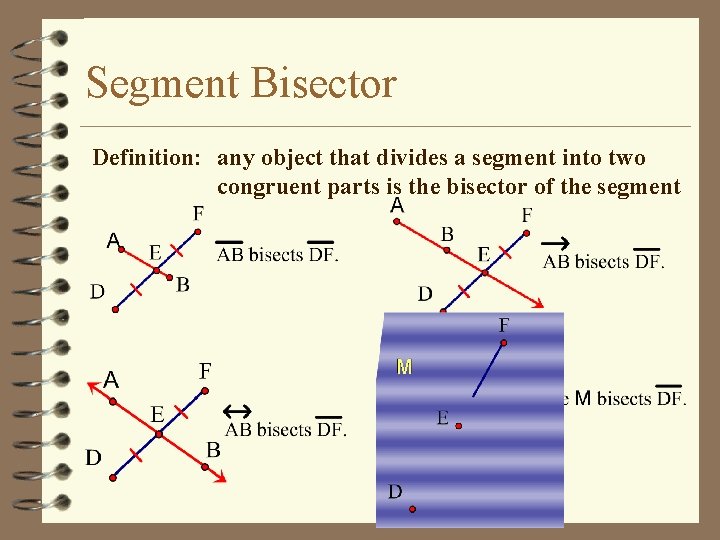
Segment Bisector Definition: any object that divides a segment into two congruent parts is the bisector of the segment M

Ray Definition: RA and all points Y such that A is between R and Y. How to sketch: How to name: ( the symbol RA is read as “ray RA” )

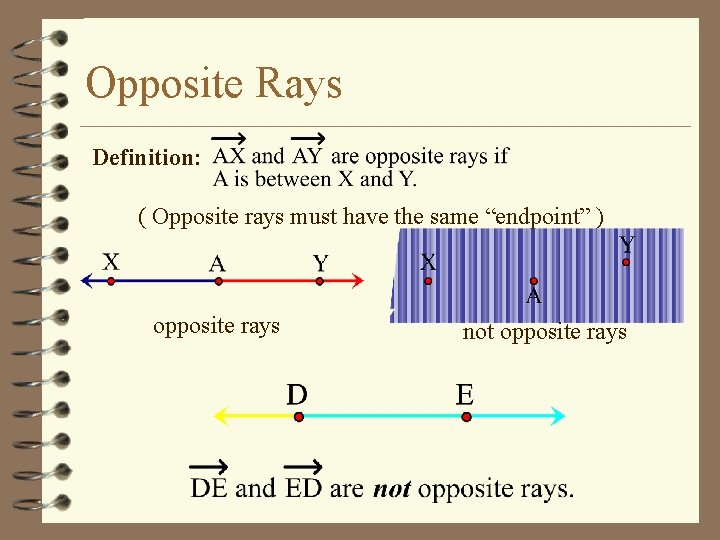
Opposite Rays Definition: ( Opposite rays must have the same “endpoint” ) opposite rays not opposite rays
 Opposite rays definition
Opposite rays definition Lesson 2 segments and rays
Lesson 2 segments and rays Lesson 1-3 segments rays parallel lines and planes
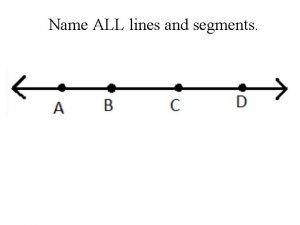
Lesson 1-3 segments rays parallel lines and planes Name
Name Division of segments and angles
Division of segments and angles Measuring segments quick check
Measuring segments quick check Measuring segments and angles
Measuring segments and angles Lesson 1 hands on angles
Lesson 1 hands on angles 1-2 skills practice line segments and distance answer
1-2 skills practice line segments and distance answer Lesson 1-2 measuring and constructing segments
Lesson 1-2 measuring and constructing segments 1-2 measuring and constructing segments lesson quiz answers
1-2 measuring and constructing segments lesson quiz answers Lesson 1-2 measuring and constructing segments
Lesson 1-2 measuring and constructing segments Postulates and theorems relating points lines and planes
Postulates and theorems relating points lines and planes