Graph Partitions Vertex partitions Partition VG into k

Graph Partitions

Vertex partitions Partition V(G) into k sets (k=3)

This kind of circle depicts an arbitrary set This kind of line means there may be edges between the two sets

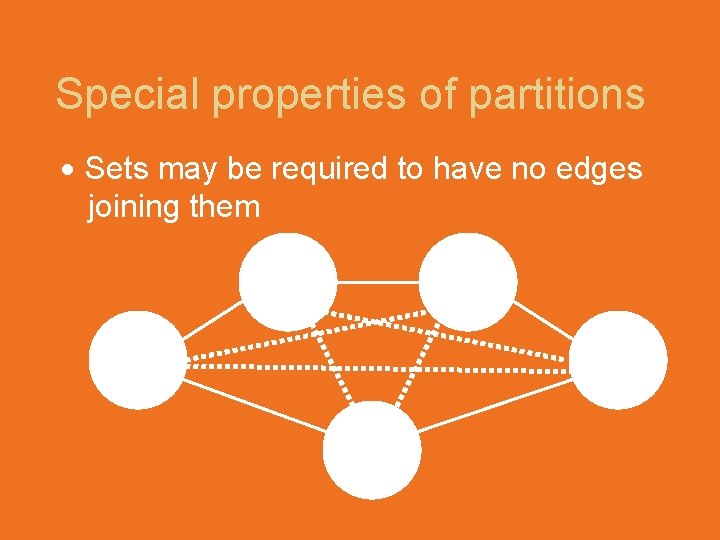
Special properties of partitions • Sets may be required to be independent

This kind of circle depicts an independent set

This is just a k-colouring (k=3)

Deciding if a k-colouring exists is in P for k =1, 2 NP-complete for all other k (k=2)

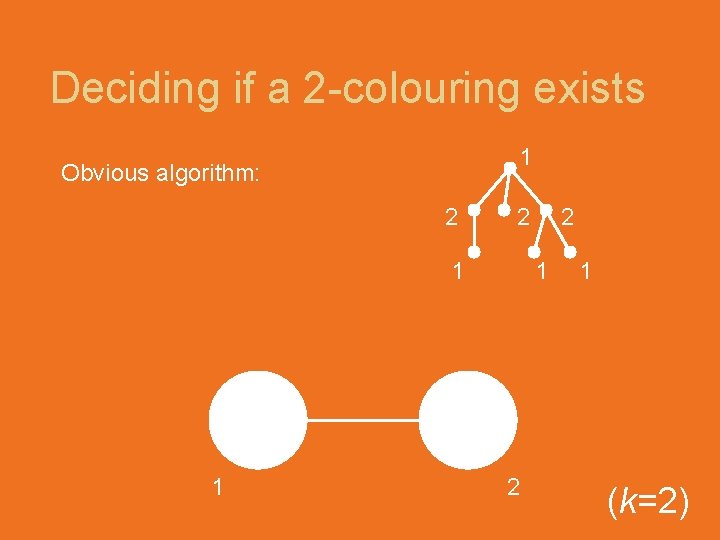
Deciding if a 2 -colouring exists 1 Obvious algorithm: 2 2 1 1 2 1 (k=2)

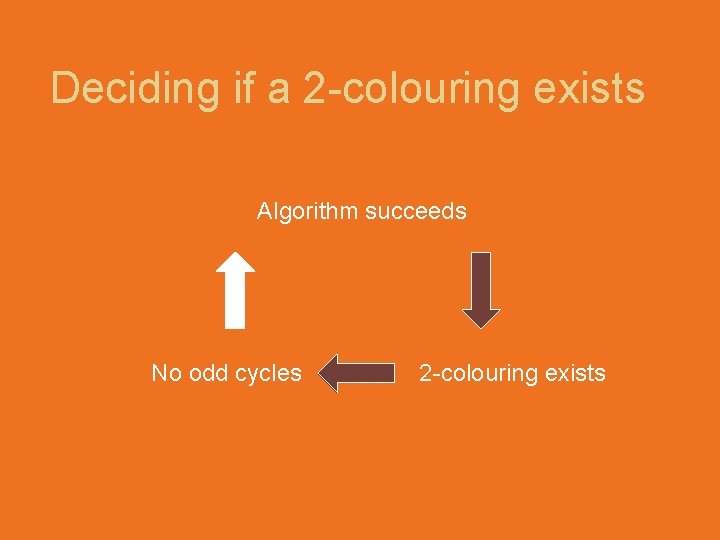
Deciding if a 2 -colouring exists Algorithm succeeds No odd cycles 2 -colouring exists

Deciding if a 2 -colouring exists Algorithm succeeds No odd cycles 2 -colouring exists

Deciding if a 2 -colouring exists Algorithm succeeds No odd cycles 2 -colouring exists

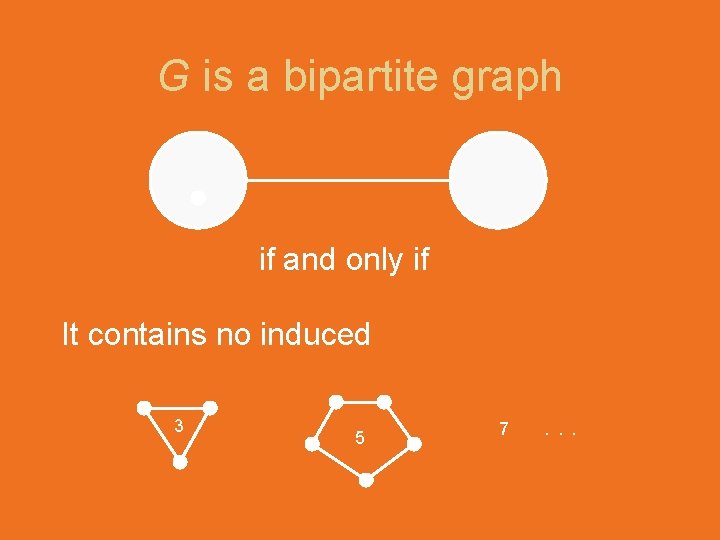
G has a 2 -colouring (is bipartite) if and only if it contains no induced 3 5 7 . . .

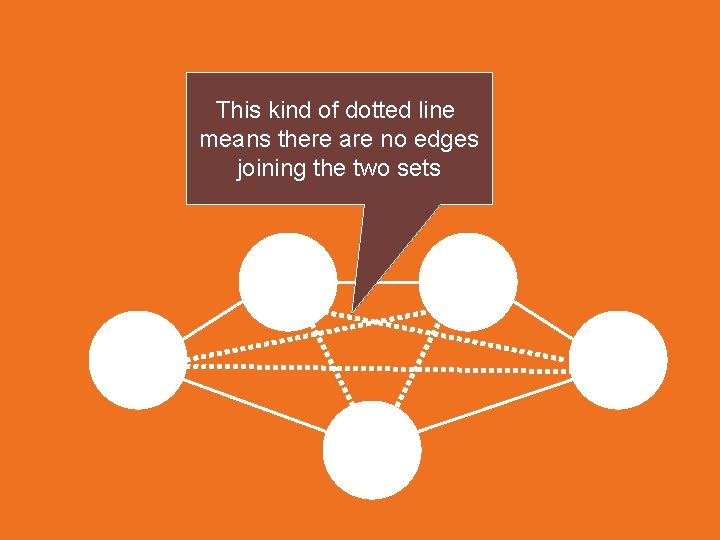
Special properties of partitions Sets may be required to have no edges joining them

This kind of dotted line means there are no edges joining the two sets

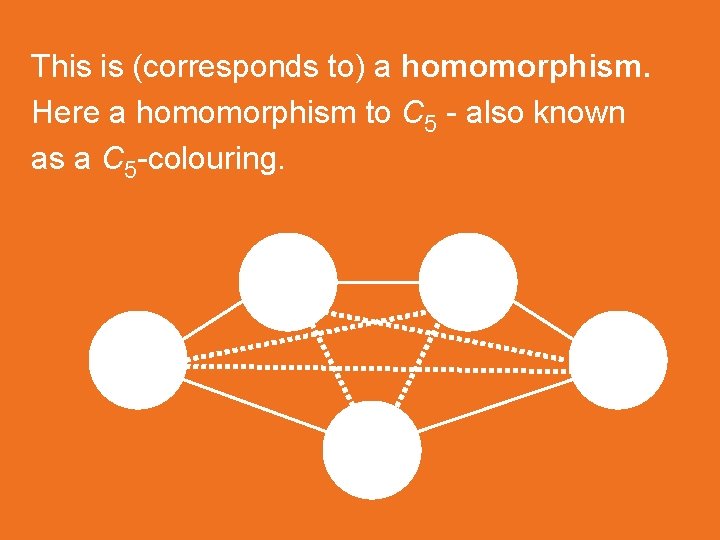
This is (corresponds to) a homomorphism. Here a homomorphism to C 5 - also known as a C 5 -colouring.

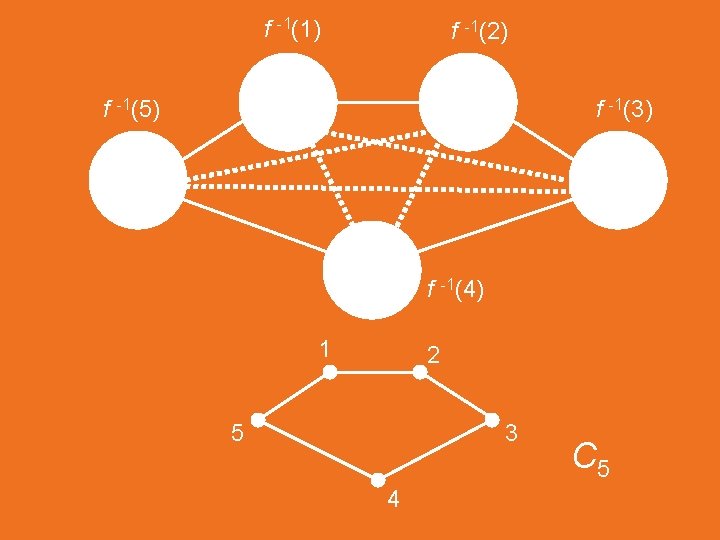
A homomorphism of G to H (or an H-colouring of G) is a mapping f : V(G) V(H) such that uv E(G) implies f(u)f(v) E(H). A homomorphism f of G to C 5 corresponds to a partition of V(G) into five independent sets with the right connections.

f -1(1) f -1(2) f -1(5) f -1(3) f -1(4) 1 2 5 3 4 C 5

1 2 5 3 4

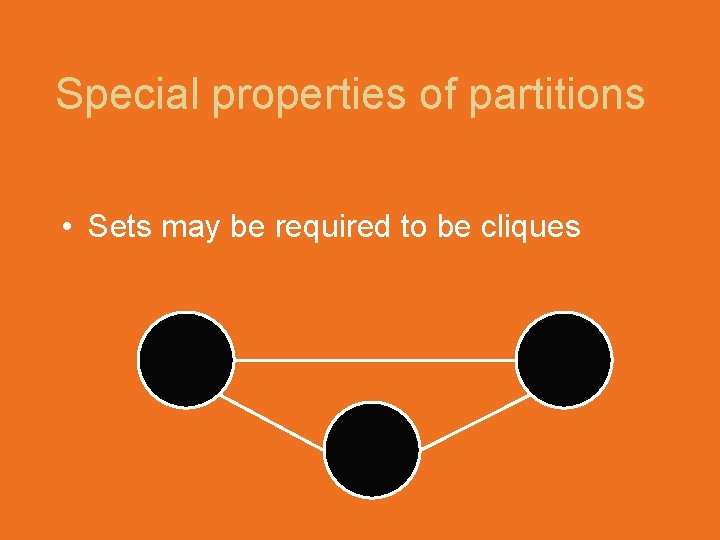
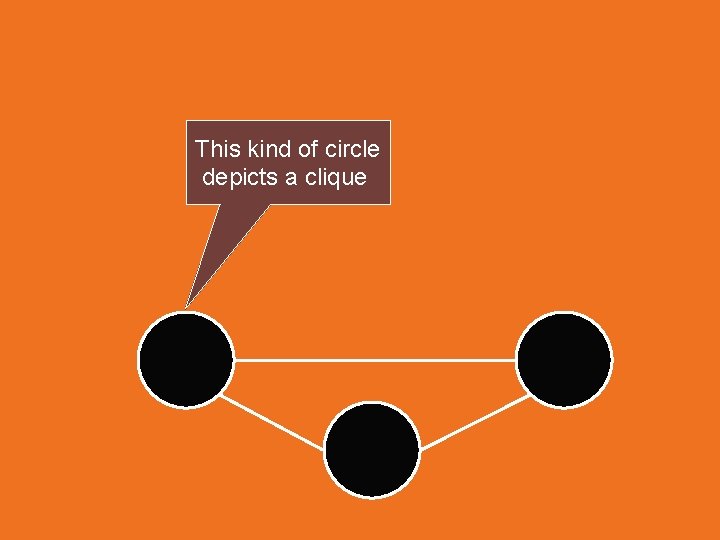
Special properties of partitions • Sets may be required to be cliques

This kind of circle depicts a clique

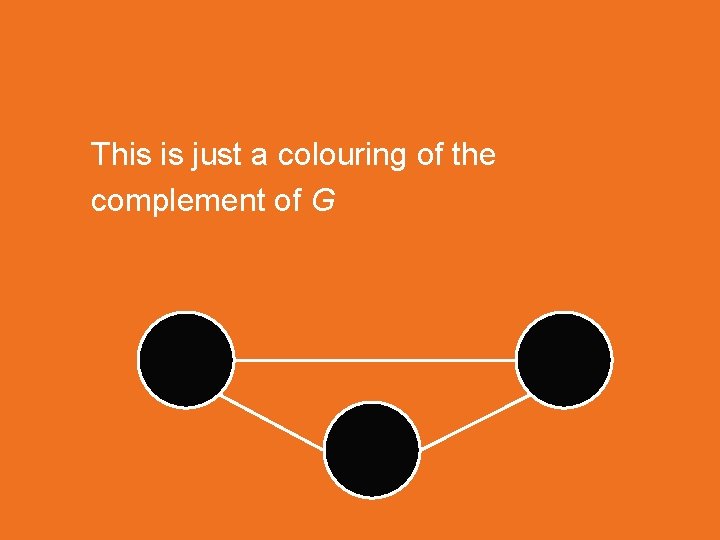
This is just a colouring of the complement of G

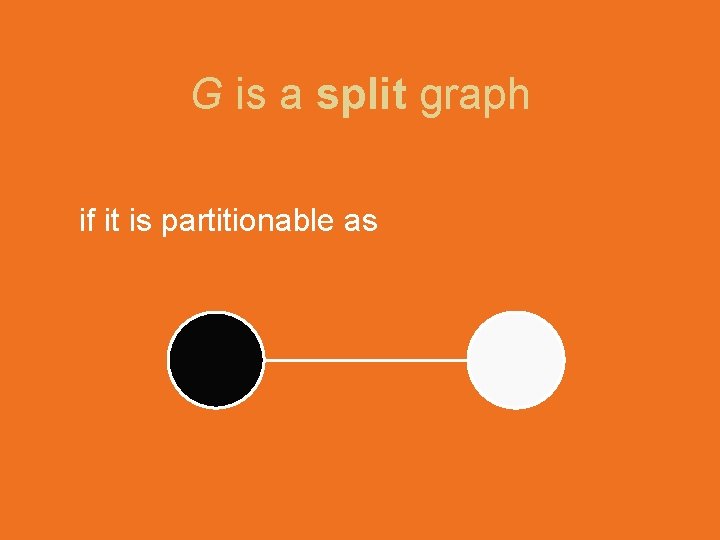
G is a split graph if it is partitionable as

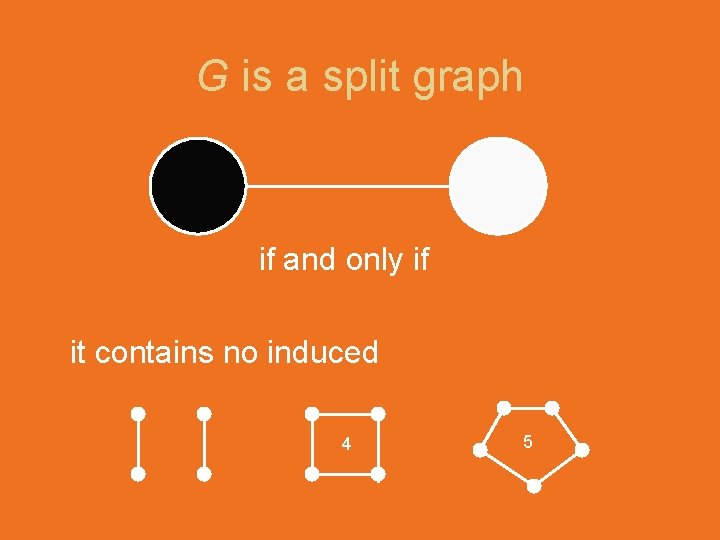
Deciding if G is a split graph is in P

G is split graph if and only if it contains no induced 4 5

Deciding if G is split Algorithm succeeds No forbidden subgraphs A splitting exists [H-Klein-Nogueira-Protti]

This is a clique cutset (assuming all parts are nonempty)

Deciding if G has a clique cutset • is in P • has applications in solving optimization problems on chordal graphs [Tarjan, Whitesides, …]

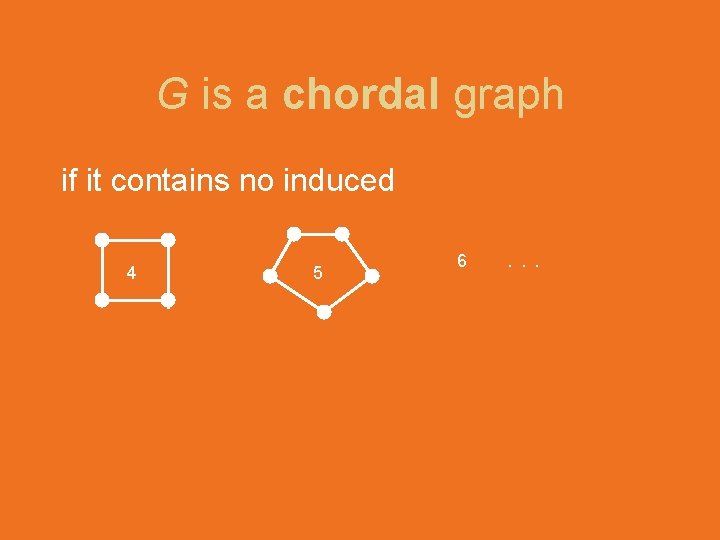
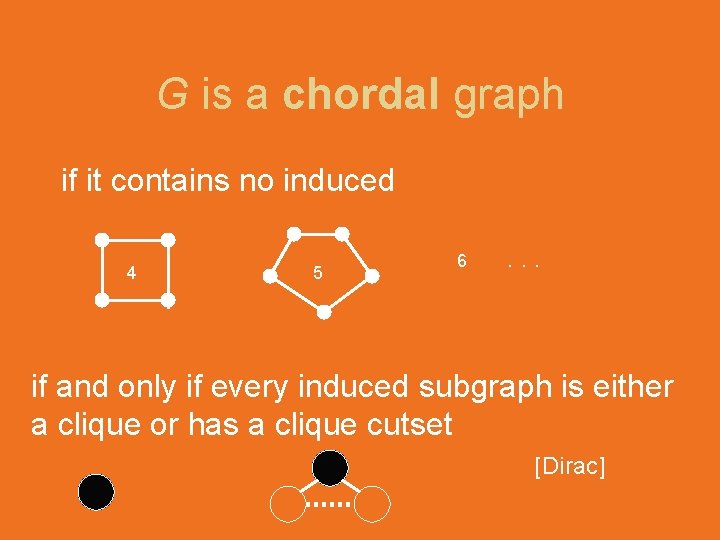
G is a chordal graph if it contains no induced 4 5 6 . . .

G is a chordal graph if it contains no induced 4 5 6 . . . if and only if every induced subgraph is either a clique or has a clique cutset [Dirac]

G is a cograph if it contains no induced

G is a cograph if it contains no induced if and only if every induced subgraph is partitionable as or [Seinsche]

This kind of line means all possible edges are present

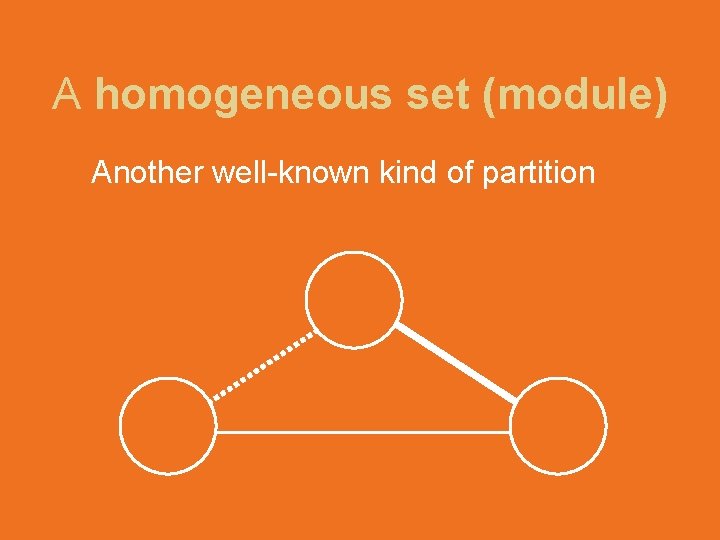
A homogeneous set (module) Another well-known kind of partition

A homogeneous set (module) • finding one is in P • has applications in decomposition and recognition of comparability graphs (and in solving optimization problems on comparability graphs) [Gallai…]

G is a perfect graph = holds for G and all its induced subgraphs.

G is a perfect graph = holds for G and all its induced subgraphs. G is perfect if and only if G and its complement contain no induced 3 5 7 . . . [Chudnovsky, Robertson, Seymour, Thomas]

Perfect graphs • contain bipartite graphs, line graphs of bipartite graphs, split graphs, chordal graphs, comparability graphs • and their complements, and • model many max-min relations. [Berge]

Perfect graphs • contain bipartite graphs, line graphs of bipartite graphs, split graphs, chordal graphs, comparability graphs • and their complements, and • model many max-min relations. Basic graphs

G is perfect if and only if it is basic or it admits a partition … all others [Chudnovsky, Robertson, Seymour, Thomas]

Special properties of partitions Sets may be required to be • Independent sets • cliques • or unrestricted Between the sets we may require no edges all edges or no restriction

The matrix M of a partition M(i, i) = 0 if Vi is independent 1 if Vi is a clique * if Vi is unrestricted M(i, j) = 0 if Vi and Vj are not joined 1 if Vi and Vj are fully joined * if Vi to Vj is unrestricted

The problem PART(M) • Instance: A graph G • Question: Does G admit a partition according to the matrix M ?

The problem SPART(M) • Instance: A graph G • Question: Does G admit a surjective partition according to M ? (the parts are non-empty)

The problem LPART(M) • Instance: A graph G, with lists • Question: Does G admit a list partition according to M ? (each vertex is placed to a set on its list)

For PART(M) we assume NO DIAGONAL ASTERISKS * M has a diagonal of k zeros and l ones (k+l=n)

Small matrices M • When |M| ≤ 4: PART(M) classified as being in P or NP-complete [Feder-H-Klein-Motwani] • When |M| ≤ 4: SPART(M) classified as being in P or NP-complete [de. Figueiredo-Klein-Gravier-Dantas] except for one matrix M

Small matrices M with lists • When |M| ≤ 4: LPART(M) classified as being in P or NP-complete, except for one matrix [Feder-H-Klein-Motwani] [de Figueiredo-Klein-Kohayakawa-Reed] [Cameron-Eschen-Hoang-Sritharan] • When |M| ≤ 3: digraph partition problems classified as being in P or NP-complete [Feder-H-Nally]

Classified PART(M) • M has no 1’s (or no 0’s) [H-Nesetril, Feder-H-Huang]

Classified PART(M) • M has no 1’s (or no 0’s) [H-Nesetril, Feder-H-Huang] PART(M) is in P if M corresponds to a graph which has a loop or is bipartite, and it is NP-complete otherwise LPART(M) is in P if M corresponds to a bi-arc graph, and it is NP-complete otherwise

Bi-Arc Graphs Defined as (complements of) certain intersection graphs… A common generalization of interval graphs (with loops) and (complements of) circular arc graphs of clique covering number two (no loops).

Classified PART(M) • M has no 1’s (or no 0’s) [H-Nesetril, Feder-H-Huang] • M has no *’s

Classified PART(M) • M has no 1’s (or no 0’s) [H-Nesetril, Feder-H-Huang] • M has no *’s All PART(M) and LPART(M) in P [Feder-H]

CSP(H) Given a structure T with vertices V(H) and relations R 1(H), … Rk(H) of arities r 1, …, rk Decide whether or not an input structure G with vertices V(G) and relations R 1(G), … Rk(G), of the same arities r 1, …, rk admits a homomorphism f of G to H. DICHOTOMY CONJECTURE [Feder-Vardi] Each CSP(H) is in P or is NP-complete

Can all PART(M) be classified? If for every matrix M the problem PART(M) is in P or is NP-complete, then the Dichotomy Conjecture is true. [Feder-H] Thus hoping to classify all problems PART(M) appears to be overly ambitious…

G is complete bipartite if and only if it contains no induced

G is a split graph if and only if it contains no induced 4 5

G is a bipartite graph if and only if It contains no induced 3 5 7 . . .

Another classification of PART(M)? For which matrices M can the problem PART(M) be described by finitely many forbidden induced subgraphs?

Infinitely many forbidden induced subgraphs occur • whenever M contains • or [Feder-H-Xie]

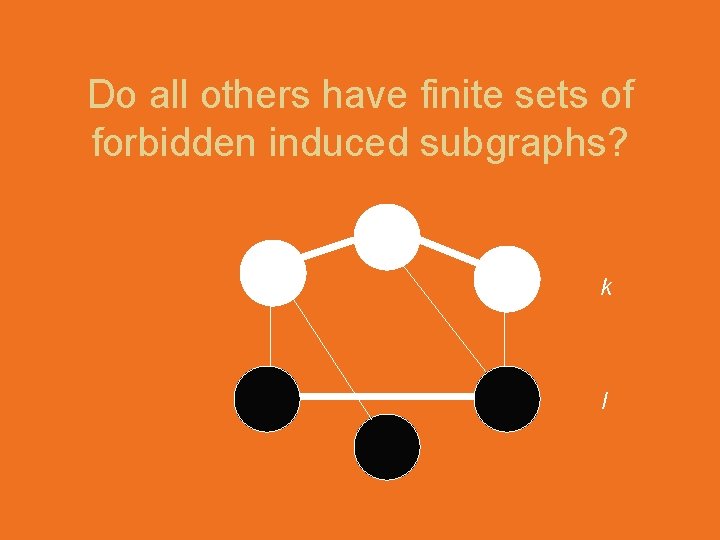
Do all others have finite sets of forbidden induced subgraphs? k l

Do all others have finite sets of forbidden induced subgraphs? NO…

For small matrices M • If |M| ≤ 5, all other partition problems have only finitely many forbidden induced subgraphs • If |M| = 6, there are other partition problems that have infinitely many forbidden induced subgraphs [Feder-H-Xie]

means without • If |M| ≤ 5, all other partition problems have only finitely many forbidden induced subgraphs • If |M| = 6, there are other partition problems that have infinitely many forbidden induced subgraphs [Feder-H-Xie]

Restrictions to inputs G Since these partitions relate closely to perfect graphs, we may want to restrict attention to (classes of) perfect graphs G

If M is normal The problem PART(M) restricted to perfect graphs G is in P [Feder-H] (fmfs)

BUT… …classifying PART(M), for perfect G, as being in P or being NP-complete, would still solve the dichotomy conjecture

If M is crossed The problem PART(M) restricted to chordal graphs G is in P [Feder-H-Klein-Nogueira-Protti]

BUT… …there are problems PART(M), restricted to chordal graphs G, which are NP-complete [Feder-H-Klein-Nogueira-Protti]

For all M A cograph G has a partition if and only if G does not contain one of a finite set of forbidden induced subgraphs [Feder-H-Hochstadter]

Are these problems CSP’s? • Yes - two adjacent vertices of G have certain allowed images in H and two nonadjacent vertices of G have certain allowed images in H. (Two binary relations)

Are these problems CSP’s? • Yes - two adjacent vertices of G have certain allowed images in H and two nonadjacent vertices of G have certain allowed images in H. (Two binary relations) • No - this is not a CSP(T), as inputs are restricted to have each pair of distinct variables in a unique binary relation.

Full CSP’s • Given a set L of positive integers, an L-full structure G has each k L elements in a unique k-ary relation • CSPL(H) is CSP(H) restricted to L-full structures G

Example with m binary relations Given a complete graph with edges coloured by 1, 2, … , m. Given such a G, colour the vertices 1, 2, …, m, without a monochromatic edge i i i

When m = 2, the problem is in P

When m = 2, the problem is in P When m 4, it is NP-complete

When m = 2, the problem is in P When m 4, it is NP-complete When m = 3, we only have algorithms of complexity [FHKS] n O ( log n / log n )

An algorithm of complexity n. O(log n) solving the (more general) problem with lists Given a complete graph G with edges coloured by 1, 2, 3, and vertices equipped with lists {1, 2, 3}

If all lists have size 2 Introduce a boolean variable for each vertex (use the first/second member of its list) Express each edge-constraint as a clause of two variables Solve by 2 -SAT

In general Let X be the set of vertices with lists {1, 2, 3} Recursively reduce |X| as follows: Try to colour G without giving any vertex its majority colour Give each vertex in turn its majority colour X X (|X|-1) / 3 X

Analysis of Recursive Algorithm Time to solve problem with |X|= x T(x) = (1 + x T(2 x/3)). T(2 -SAT)

Analysis of Recursive Algorithm Time to solve problem with |X|= x T(x) = (1 + x T(2 x/3)). T(2 -SAT) T(x) = x O(log x)

Analysis of Recursive Algorithm Time to solve problem with |X|= x T(x) = (1 + x T(2 x/3)). T(2 -SAT) T(x) = x O(log x) T(n) = n O(log n)

Can we say anything ? A kind of (quasi) dichotomy If 1 L then every CSPL(H) is quasi-polynomial or NP-complete [Feder-H]