Chapter 4 Partition 2 Multilayer Partition DingZhu Du

Intersection Disk Graph Consider n points in the Euclidean plane, each is associated with

Maximum Independent Set in Intersection Disk Graph Given a intersection disk graph D, find

Multi-layer Suppose the largest disk has diameter 1 -ε. Let dmin be The diameter

A disk hits a cut line. At each layer, a disk can hit at

D(a, b) In partition P(a, b), delete all disks each hitting a cut line

Dynamic Programming j-cell is a cell in layer j. For any j-cell S and

# of Table(S, I) # of S = too large How do we overcome

Dynamic Programming j-cell is a cell in layer j. For any relevant j-cell S

Maximal relevant cell A relevant cell is maximal if it is not contained by

# of Table(S, I) # of relevant S = n. # of I =

Computation Time of Recursion # of S’ = # of J = Time =

(1+ε)-Approximation Choose k = ? . Compute opt(D(0, 0)), opt(D(1, 1)), …, opt(D(k-1, k-1).

Analysis • Consider an optimal solution D*. • For each partition P(a, b), let

|H(0, 0)|+|H(1, 1)|+···+|H(k-1, k-1)| Each disk appears in at most two terms in this

Performance ratio Opt/approx =1/(1 -2/k) = 1 + 2/(k-4) Choose We obtain a (1+ε)-approximation

Slides: 26

Download presentation

Chapter 4. Partition (2) Multi-layer Partition Ding-Zhu Du

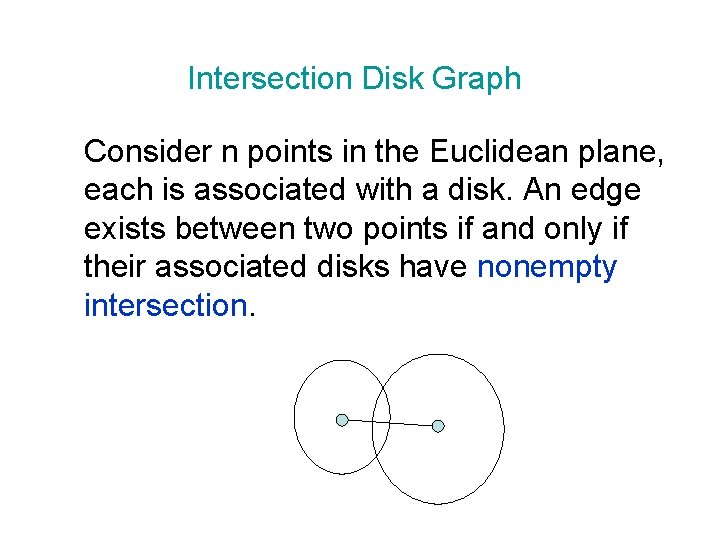
Intersection Disk Graph Consider n points in the Euclidean plane, each is associated with a disk. An edge exists between two points if and only if their associated disks have nonempty intersection.

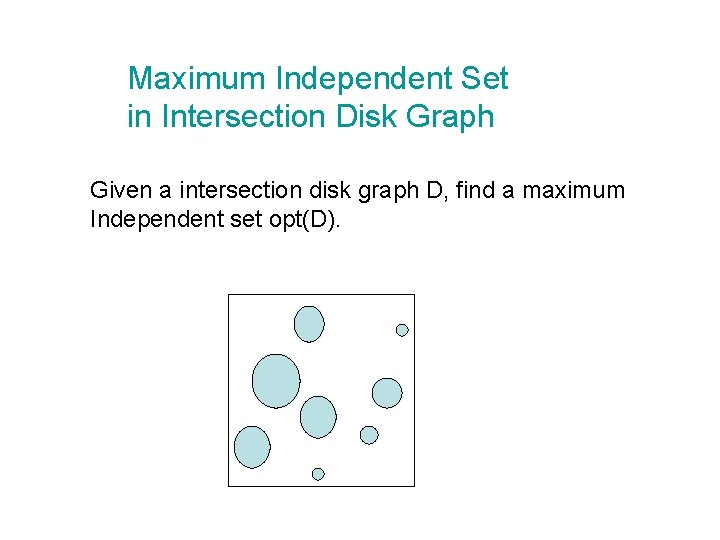
Maximum Independent Set in Intersection Disk Graph Given a intersection disk graph D, find a maximum Independent set opt(D).

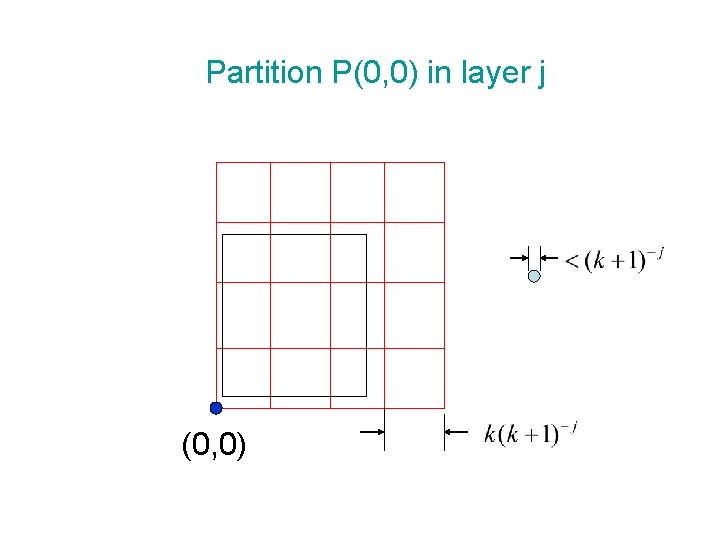
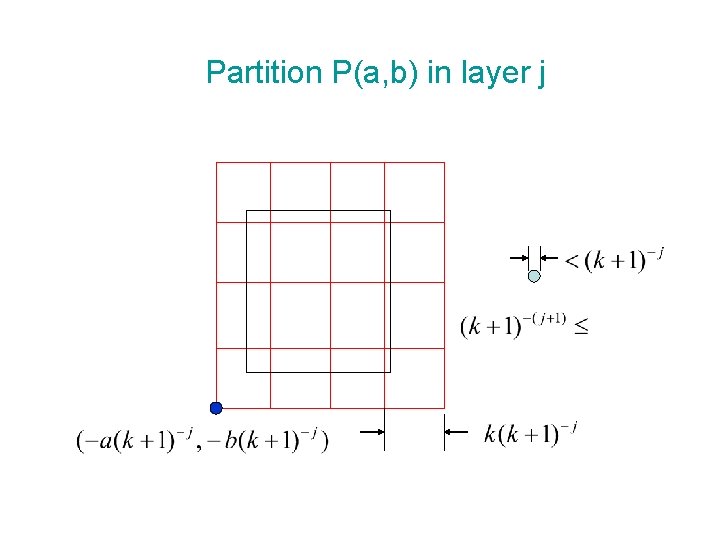
Multi-layer Suppose the largest disk has diameter 1 -ε. Let dmin be The diameter of smallest disk. Fix an integer k > 0. Let Put all disks into m+1 layers. For 0 < j < m, layer j consists of all disks with diameter di,

Partition P(0, 0) in layer j (0, 0)

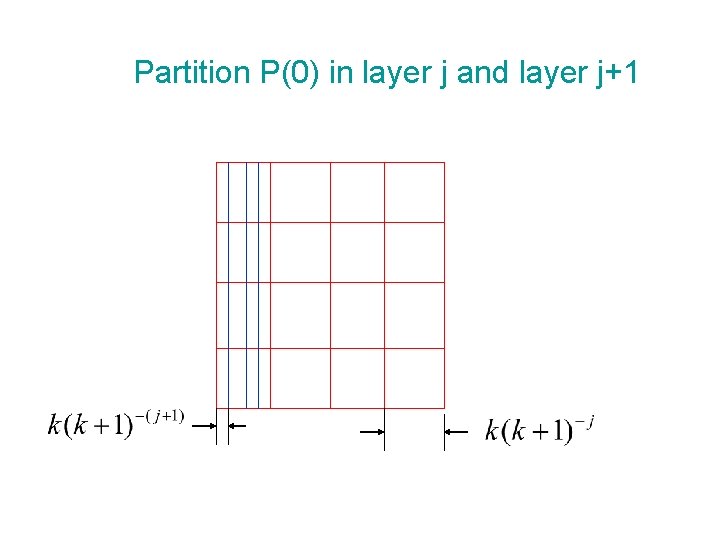
Partition P(0) in layer j and layer j+1

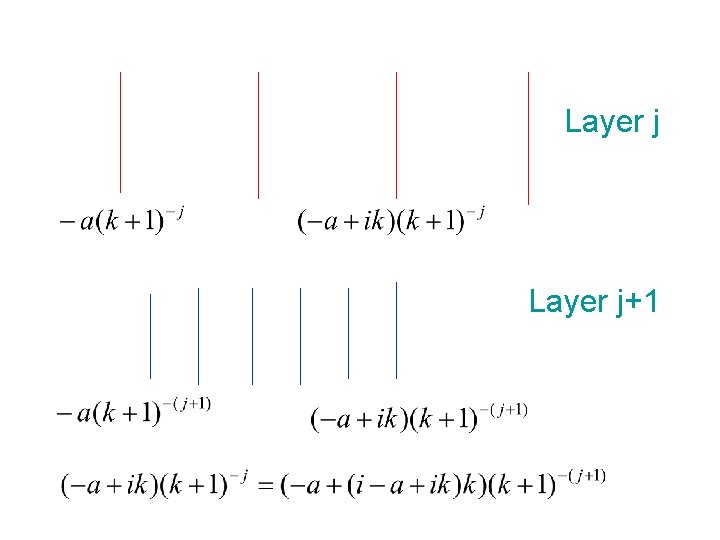
Partition P(a, b) in layer j

Layer j+1

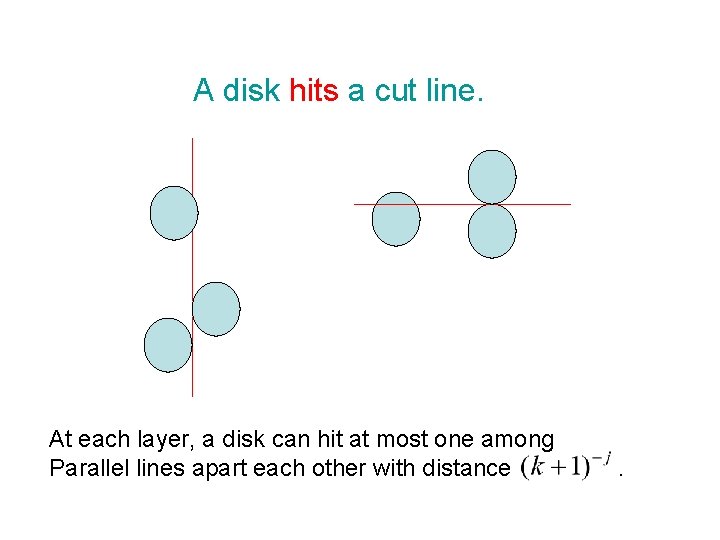
A disk hits a cut line. At each layer, a disk can hit at most one among Parallel lines apart each other with distance .

D(a, b) In partition P(a, b), delete all disks each hitting a cut line in the same layer. The remaining disks form a collection D(a, b). Maximum Independent set opt(D(a, b)) can be computed in time by dynamic programming. Why use it?

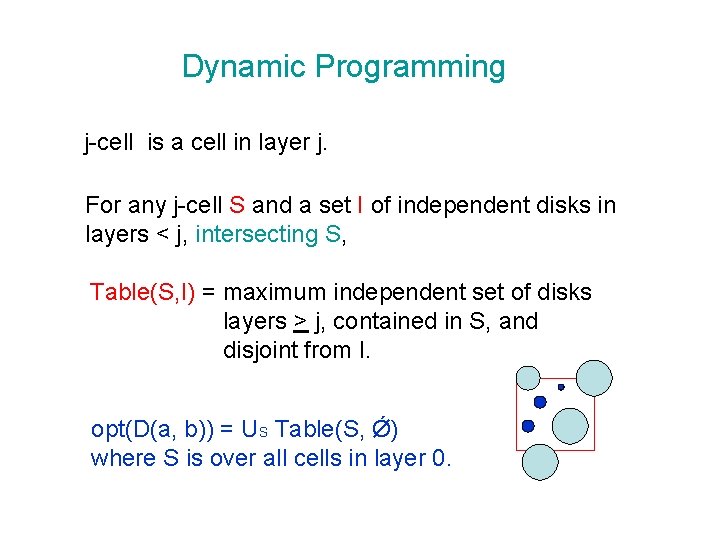
Dynamic Programming j-cell is a cell in layer j. For any j-cell S and a set I of independent disks in layers < j, intersecting S, Table(S, I) = maximum independent set of disks layers > j, contained in S, and disjoint from I. opt(D(a, b)) = US Table(S, Ǿ) where S is over all cells in layer 0.

Recursive Relation For j-cell S and I,

# of Table(S, I) # of S = too large How do we overcome this difficulty? Relevant cell: A j-cell is relevant if it contains a disk in layer j.

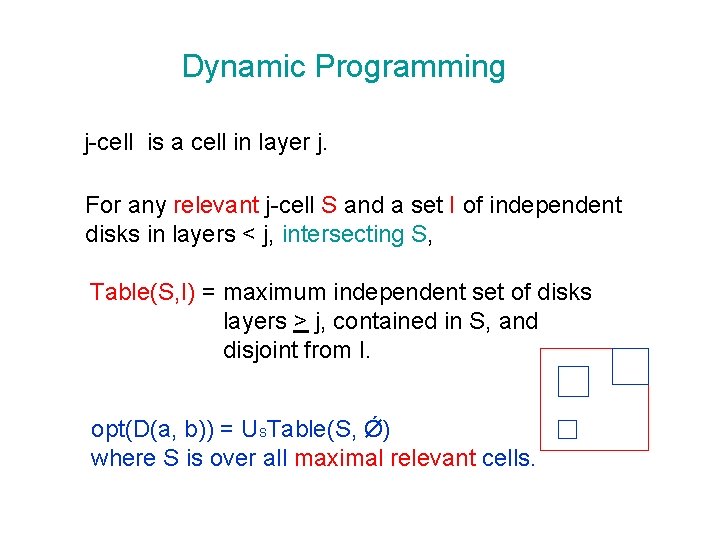
Dynamic Programming j-cell is a cell in layer j. For any relevant j-cell S and a set I of independent disks in layers < j, intersecting S, Table(S, I) = maximum independent set of disks layers > j, contained in S, and disjoint from I. opt(D(a, b)) = USTable(S, Ǿ) where S is over all maximal relevant cells.

Children of a relevant cell S’ S’’ S

Maximal relevant cell A relevant cell is maximal if it is not contained by Another relevant cell.

Recursive Relation For j-cell S,

# of Table(S, I) # of relevant S = n. # of I = # of Table(S, I) =

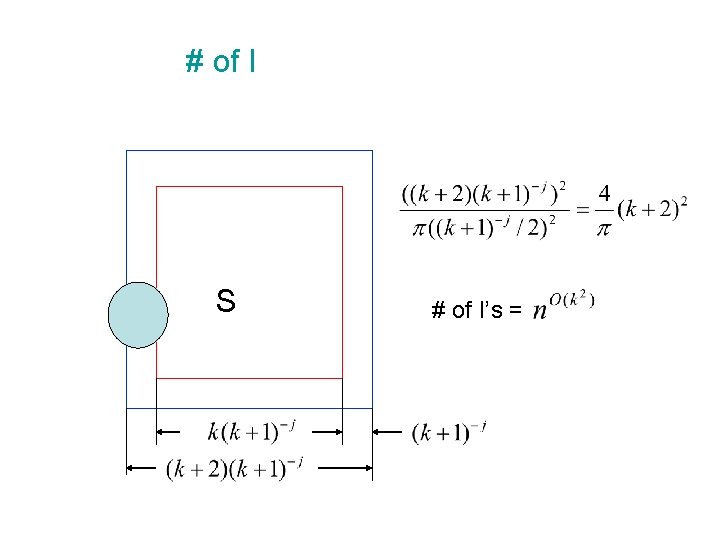
# of I S # of I’s =

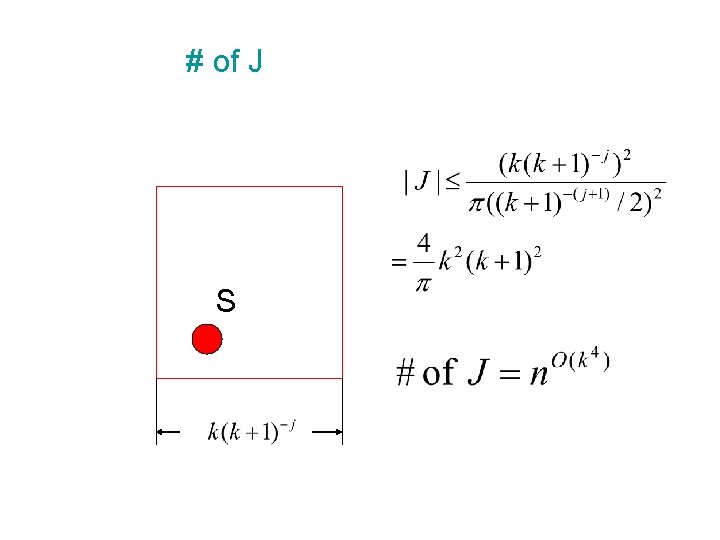
Computation Time of Recursion # of S’ = # of J = Time = Running Time of dynamic programming

# of J S

(1+ε)-Approximation Choose k = ? . Compute opt(D(0, 0)), opt(D(1, 1)), …, opt(D(k-1, k-1). Choose maximum one among them.

Analysis • Consider an optimal solution D*. • For each partition P(a, b), let H(a, b) be the collection of all disks hitting cut line in the same layer. • Estimate |H(0, 0)|+|H(1, 1)|+···+|H(k-1, k-1)|.

|H(0, 0)|+|H(1, 1)|+···+|H(k-1, k-1)| Each disk appears in at most two terms in this sum. There exists i such that |H(2 i, 2 i)| < 2|D*|/k.

Performance ratio Opt/approx =1/(1 -2/k) = 1 + 2/(k-4) Choose We obtain a (1+ε)-approximation With time

Thanks, End