SIGMOD 2007 Trajectory Clustering A PartitionandGroup Framework June

SIGMOD 2007 Trajectory Clustering: A Partition-and-Group Framework June 13, 2007 Jae-Gil Lee 1), Jiawei Han 1), and Kyu-Young Whang 2) 1) 2) 6/13/07 Dept. of Computer Science, UIUC, USA Dept. of Computer Science, KAIST, Korea Trajectory Clustering: A Partition-and-Group Framework

Table of Contents = Motivation = Partition-and-Group Framework = Trajectory Clustering Algorithm: TRACLUS • Partitioning Phase • Grouping Phase = Performance Evaluation = Related Work = Conclusions 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 2

Clustering = Definition: the process of grouping a set of physical or abstract objects into classes of similar objects [11] = Applications: market research, pattern recognition, data analysis, image processing, etc. = Representative algorithms: k-means [17], BIRCH [24], DBSCAN [6], OPTICS [2], and STING [22] = Target data: previous research has mainly dealt with clustering of point data 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 3

Analysis on Trajectory Data = A tremendous amount of trajectory data of moving objects is being collected • Example: vehicle position data, hurricane track data, animal movement data, etc. = A typical data analysis task is to find objects that have moved in a similar way An efficient clustering algorithm for trajectories is urgently required 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 4

Limitations of Existing Algorithms = The algorithm proposed by Gaffney et al. [7, 8] clusters trajectories as a whole = Clustering trajectories as a whole could not detect similar portions of the trajectories (i. e. , common sub-trajectories) • Example: if we cluster TR 1~TR 5 as a whole, we cannot discover the common behavior since they move to totally different directions TR 3 TR 4 TR 5 A common sub-trajectory TR 2 TR 1 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 5

Discovery of Common Sub-Trajectories = Discovering common sub-trajectories is very useful, especially if we have regions of special interest 1) Hurricane Landfall Forecasts [18] Meteorologists will be interested in the common behaviors of hurricanes near the coastline or at sea (i. e. , before landing) 2) Effects of Roads and Traffic on Animal Movements [23] Zoologists will be interested in the common behaviors of animals near the road where the traffic rate has been varied = Our solution is to partition a trajectory into a set of line segments and then group similar line segments A partition-and-group framework 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 6

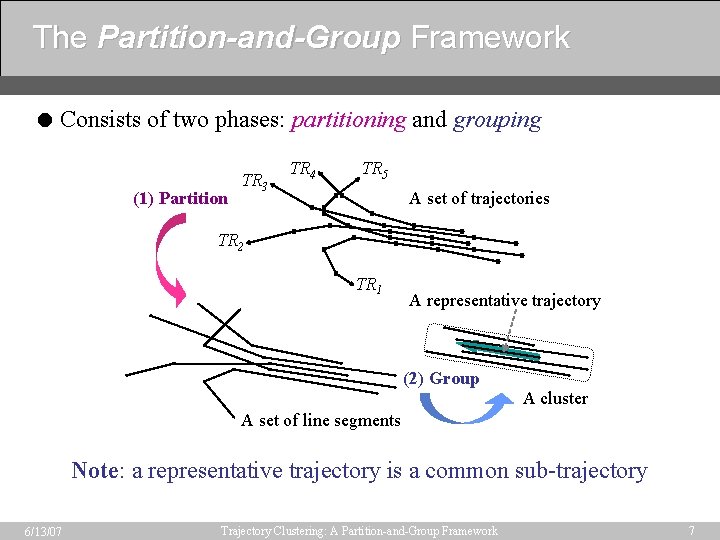
The Partition-and-Group Framework = Consists of two phases: partitioning and grouping (1) Partition TR 3 TR 4 TR 5 A set of trajectories TR 2 TR 1 A representative trajectory (2) Group A cluster A set of line segments Note: a representative trajectory is a common sub-trajectory 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 7

Problem Statement = Given a set of trajectories I = {TR 1, …, TRn}, our algorithm generates a set of clusters O = {C 1, …, Cm} as well as a representative trajectory for each cluster Ci = Necessary definitions: • A trajectory is a sequence of multi-dimensional points, which is denoted as TRi = p 1 p 2 p 3 … pj … pleni • A cluster is a set of trajectory partitions; a trajectory partition is a line segment pipj (i < j), where pi and pj are the points chosen from the same trajectory • A representative trajectory is an imaginary trajectory that indicates the major behavior of the trajectory partitions 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 8

The Clustering Algorithm: TRACLUS = Based on the partition-and-group framework Algorithm TRACLUS Input: A set of trajectories I = {TR 1, …, TRn} Output: (1) A set of clusters O = {C 1, …, Cm} (2) A set of representative trajectories Algorithm: /* Partitioning Phase */ 01: for each TR I do 02: Partition TR into a set L of line segments; 03: Accumulate L into a set D; /* Grouping Phase */ 04: Group D into a set O of clusters; 05: for each C O do 06: Generate a representative trajectory for C; 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 9

Current Step (1/3) Algorithm TRACLUS /* Partitioning Phase */ 01: for each TR I do 02: Partition TR into a set L of line segments; 03: Accumulate L into a set D; /* Grouping Phase */ 04: Group D into a set O of clusters; 05: for each C O do 06: Generate a representative trajectory for C; 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 10

Characteristic Points = Identify the points where the behavior of a trajectory changes rapidly; such points are called characteristic points : characteristic point : trajectory partition = A trajectory is partitioned at every characteristic point = A line segment between consecutive characteristic points is called a trajectory partition 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 11

Desirable Properties of Trajectory Partitioning = Preciseness: the difference between a trajectory and a set of its trajectory partitions should be as small as possible = Conciseness: the number of trajectory partitions should be as small as possible Note: two properties are contradictory to each other conciseness preciseness characteristic points = starting and ending points characteristic points = all points We need to find the optimal tradeoff 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 12

Minimum Description Length (MDL) Principle = The MDL principle has been widely used in information theory = The MDL cost consists of two components [9]: L(H) and L(D|H), where H means the hypothesis, and D the data • L(H) is the length, in bits, of the description of the hypothesis • L(D|H) is the length, in bits, of the description of the data when encoded with the help of the hypothesis = The best hypothesis H to explain D is the one that minimizes the sum of L(H) and L(D|H) 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 13

Translation into MDL Optimization = Finding the optimal partitioning translates to finding the best hypothesis using the MDL principle • H a set of trajectory partitions, D a trajectory • L(H) the sum of the length of all trajectory partitions • L(D|H) the sum of the difference between a trajectory and a set of its trajectory partitions = L(H) measures conciseness; L(D|H) preciseness 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 14

Approximate Trajectory Partitioning = The cost of finding the optimal partitioning is prohibitive = Use an approximate algorithm; our approximation is to regard the set of local optima as the global optimum = Algorithm skeleton (See Fig. 8 in the paper): • Compute the MDL costs both when a point pk is a characteristic point and when it is not Choose pk-1 as a characteristic point, if the former > the latter Advance pk by increasing k, otherwise approximate solution 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 15

Current Step (2/3) Algorithm TRACLUS /* Partitioning Phase */ 01: for each TR I do 02: Partition TR into a set L of line segments; 03: Accumulate L into a set D; /* Grouping Phase */ 04: Group D into a set O of clusters; 05: for each C O do 06: Generate a representative trajectory for C; 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 16

Distance between Line Segments = The weighted sum of three components: the perpendicular distance( ), parallel distance( ), and angle distance( ) • Adapted from similarity measures used in the domain of pattern recognition [4] Remark: the sum of the distances between endpoints does not work well for line segment clustering 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 17

Density of Line Segments = Change the definitions for points, originally proposed for DBSCAN [6], to those for line segments = Def. (ε-neighborhood): Nε(Li) = {Lj ∈ D | dist(Li, Lj) ≤ ε} = Def. (core line segment): Li is a core line segment w. r. t. ε and Min. Lns if |Nε(Li)| ≥ Min. Lns = Def. (directly density-reachable): Li directly density-reachable from Lj w. r. t. ε and Min. Lns if Li ∈ Nε(Lj) and |Nε(Lj)| ≥ Min. Lns = Def. (density-reachable): Transitive closure of directly density-reachability = Def. (density-connected set ≡ cluster): 1) Maximal w. r. t. density-reachability 2) Any line segments are density-connected, i. e. , density-reachable from a third line segment 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 18

Density of Line Segments (cont’d) = Example: • • L 1, L 2, L 3, L 4, and L 5 are core line segments L 2 (or L 3) is directly density-reachable from L 1 L 6 is density-reachable from L 1, but not vice versa L 1, L 4, and L 5 are all density-connected L 5 L 3 L 4 L 2 L 1 Min. Lns = 3 L 6 L 5 L 3 L 1 L 2 L 4 Note: the shape of an ε-neighborhood is likely to be an ellipse rather than a circle 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 19

Examples of ε-neighborhoods Red lines: core line segments, Blue lines: line segments in the ε-neighborhood 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 20

Line Segment Clustering = Algorithm skeleton (See Fig. 8 in the paper): 1. Select an unprocessed line segment L 2. Retrieve all line segments density-reachable from L w. r. t. ε and Min. Lns • • If L is a core line segment, a cluster is formed Otherwise, L is marked as a noise 3. Continue this process until all line segments have been processed 4. Filter out clusters whose trajectory partitions have been extracted from too few trajectories = Time complexity (See Lemma 3 in the paper): • • 6/13/07 O(n 2): if an index does not exist O(nlogn): if an index does exist Trajectory Clustering: A Partition-and-Group Framework 21

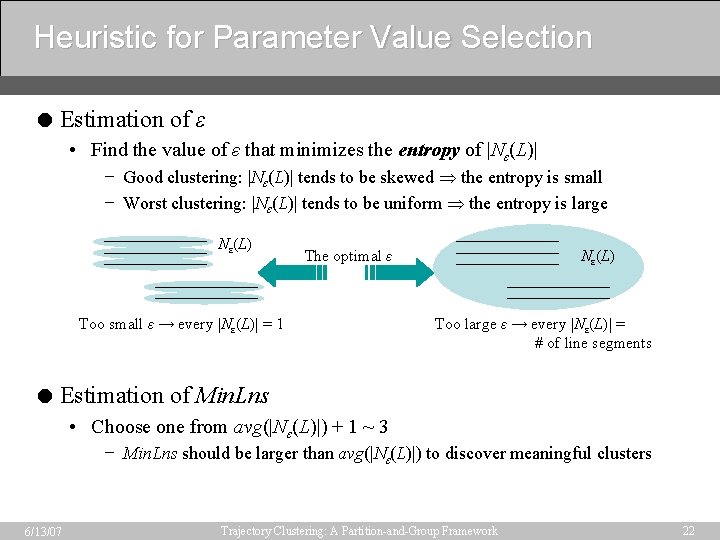
Heuristic for Parameter Value Selection = Estimation of ε • Find the value of ε that minimizes the entropy of |Nε(L)| − Good clustering: |Nε(L)| tends to be skewed the entropy is small − Worst clustering: |Nε(L)| tends to be uniform the entropy is large Nε(L) The optimal ε Too small ε → every |Nε(L)| = 1 Nε(L) Too large ε → every |Nε(L)| = # of line segments = Estimation of Min. Lns • Choose one from avg(|Nε(L)|) + 1 ~ 3 − Min. Lns should be larger than avg(|Nε(L)|) to discover meaningful clusters 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 22

Current Step (3/3) Algorithm TRACLUS /* Partitioning Phase */ 01: for each TR I do 02: Partition TR into a set L of line segments; 03: Accumulate L into a set D; /* Grouping Phase */ 04: Group D into a set O of clusters; 05: for each C O do 06: Generate a representative trajectory for C; 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 23

Representative Trajectories = Describe the overall movement of the trajectory partitions that belong to the cluster = Correspond to common sub-trajectories = Can be considered a model [1] for clusters = Useful for domain experts to understand the movement in the trajectories 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 24

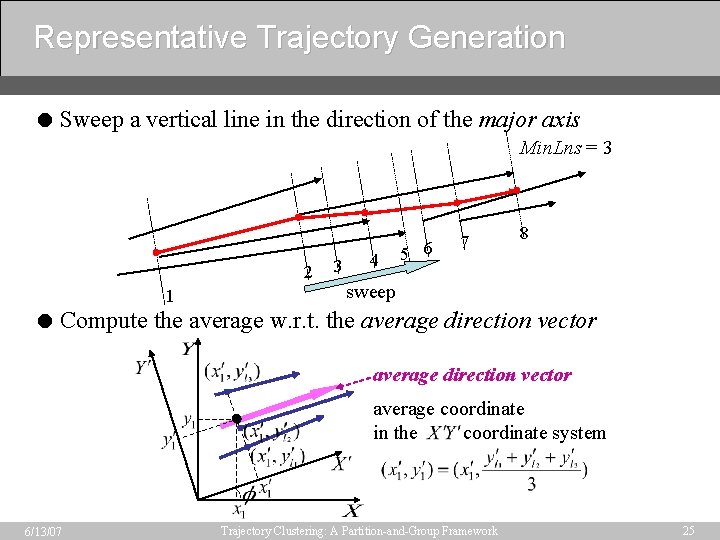
Representative Trajectory Generation = Sweep a vertical line in the direction of the major axis Min. Lns = 3 2 1 3 4 5 6 7 8 sweep = Compute the average w. r. t. the average direction vector average coordinate in the coordinate system 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 25

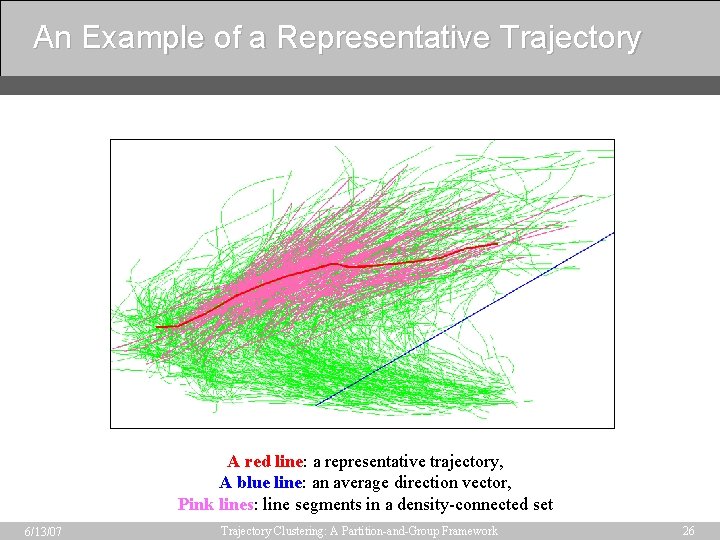
An Example of a Representative Trajectory A red line: a representative trajectory, A blue line: an average direction vector, Pink lines: line segments in a density-connected set 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 26

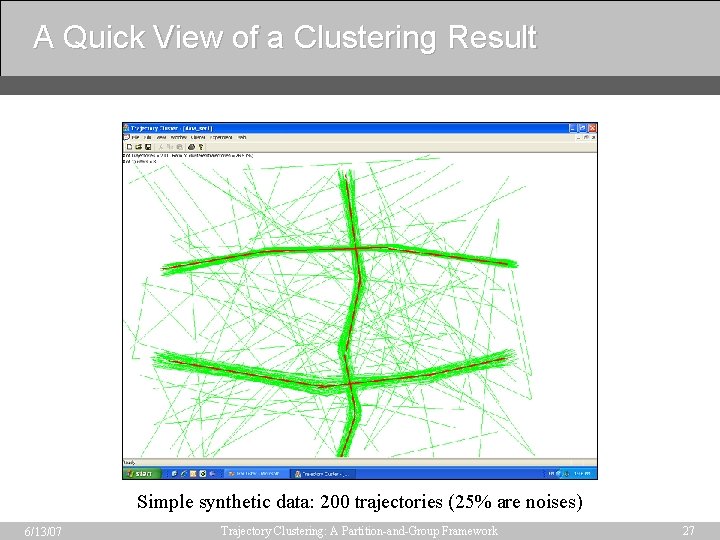
A Quick View of a Clustering Result Simple synthetic data: 200 trajectories (25% are noises) 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 27

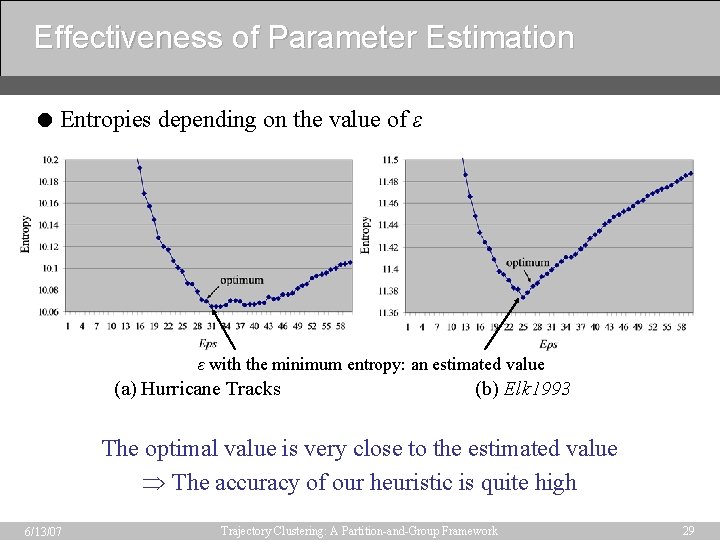
Performance Evaluation = Use two real trajectory data sets • Hurricane track data set − Record the Atlantic hurricanes from the years 1950 through 2004 − Contain 570 trajectories and 17, 736 points • Animal movement data set − Record the locations of elk, deer, and cattle from the years 1993 through 1996 (the Starkey project) − Elk 1993: Contain 33 trajectories and 47, 204 points; Deer 1995: Contain 32 trajectories and 20, 065 points = Validate the clustering quality 1) Estimate the parameter values for ε and Min. Lns 2) Try a few values around the estimated ones; determine the optimal parameter values by visual inspection 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 28

Effectiveness of Parameter Estimation = Entropies depending on the value of ε ε with the minimum entropy: an estimated value (a) Hurricane Tracks (b) Elk 1993 The optimal value is very close to the estimated value The accuracy of our heuristic is quite high 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 29

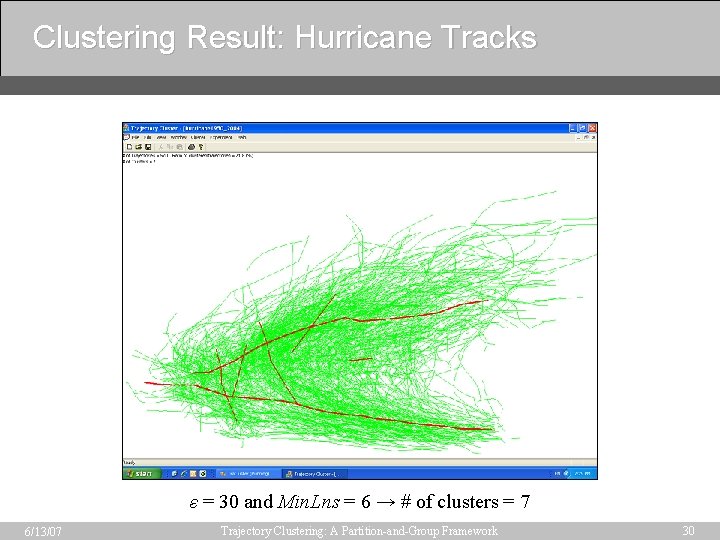
Clustering Result: Hurricane Tracks ε = 30 and Min. Lns = 6 → # of clusters = 7 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 30

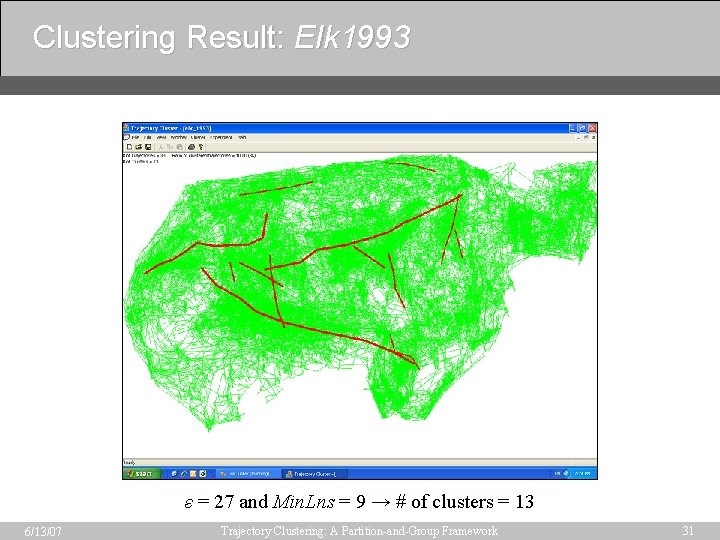
Clustering Result: Elk 1993 ε = 27 and Min. Lns = 9 → # of clusters = 13 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 31

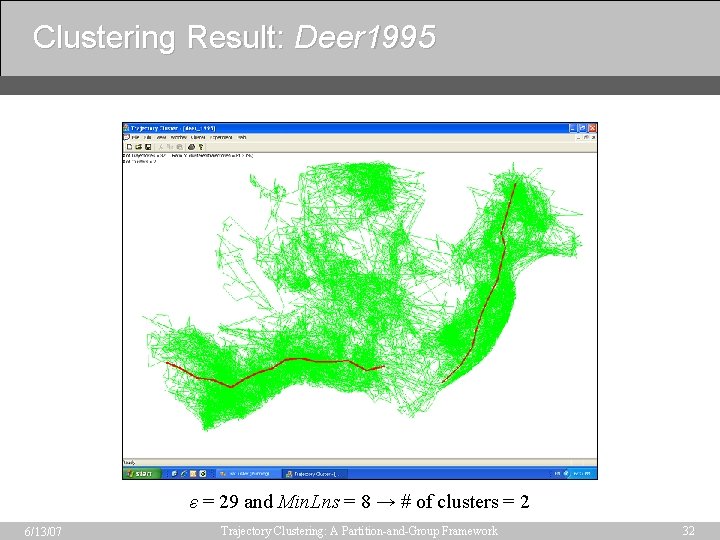
Clustering Result: Deer 1995 ε = 29 and Min. Lns = 8 → # of clusters = 2 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 32

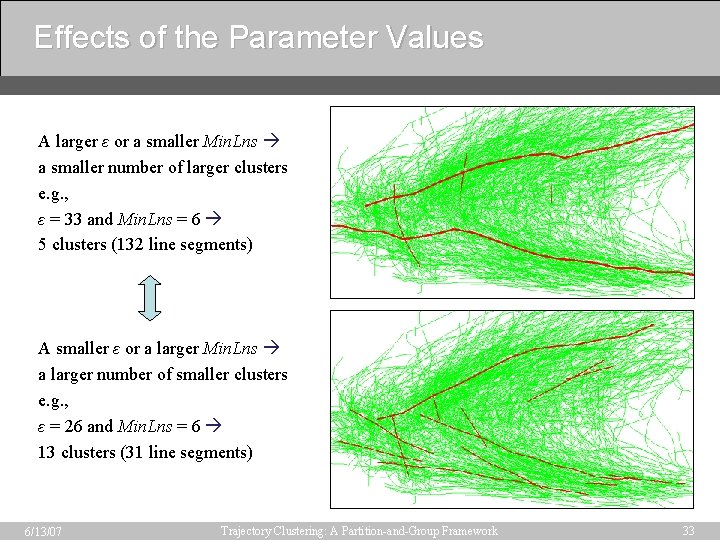
Effects of the Parameter Values A larger ε or a smaller Min. Lns a smaller number of larger clusters e. g. , ε = 33 and Min. Lns = 6 5 clusters (132 line segments) A smaller ε or a larger Min. Lns a larger number of smaller clusters e. g. , ε = 26 and Min. Lns = 6 13 clusters (31 line segments) 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 33

Related Work = Clustering algorithms for points = Clustering algorithms for trajectories [7, 8] • Based on probabilistic clustering • Cluster trajectories as a whole = Distance measures for trajectories: LCSS [21] and EDR [5] • Based on the edit distance • Designed to compare the whole trajectory (time series) = Applications of the MDL principle [3, 13] • Graph partitioning (cross-association) • Distance function design for strings: CDM = Polyline simplification • Require additional parameters • Developed mainly for the Euclidean distance 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 34

Challenging Issues = Efficiency • Use an index to execute ε-neighborhood queries • Not easy because our distance function is non-metric = Parameter insensitivity • Make our algorithm more insensitive to parameter values = Movement patterns • Support various types of movement patterns, especially circular motion = Temporal information • Take account of temporal information during clustering 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 35

Conclusions = Proposed a novel framework, the partition-and-group framework, for clustering trajectories = Developed the trajectory clustering algorithm TRACLUS based on this framework = Demonstrated the effectiveness of TRACLUS using various real trajectory data Provided a new paradigm in trajectory clustering 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 36

Thank You! 6/13/07 Trajectory Clustering: A Partition-and-Group Framework 37