Geometry Chapter 2 Reasoning and Proof L2 1

Geometry Chapter #2 Reasoning and Proof

L#2. 1 A Conditional Statements A conditional statement has two parts: 1. The hypothesis----the “if” part hypothesis 2. The conclusion----the “then” part conclusion Example: If an animal has feathers, then it is a bird. Hypothesis: “If an animal has feathers, ” Conclusion: “then it is a bird. ” The “if” does not always have to be at the beginning, and the “then” does not always have to be at the end. Sometimes the words “if” and “then” are not even used in the conditional statement.

A conditional statement MAY or MAY NOT be a true statement. True Conditional Statement If an animal has feathers, then it is a bird. This is TRUE since all birds have feathers. False Conditional Statement If it is Friday, then we will have chapel. This is FALSE since there are many Fridays when we do not have school and so we do not have chapel.

To show a conditional statement is false, you must provide a counterexample. For the conditional statement, “If it is Friday, then we will have chapel, ” we must give an example of a Friday when we do not have chapel. There are several counterexamples for this conditional statement, but one would be Friday, October 9. On that Friday, we have the Walk-a-Thon, and we will not have chapel.

The Converse of a Conditional Statement The converse of a conditional statement is formed by SWITCHING the hypothesis and conclusion. Example: If an animal is a bird, then it has feathers. Example: If we have chapel, then it is a Friday. Converses MAY or MAY NOT be true. In the first example, the converse is true. If an animal is a bird, then it has feathers since all birds have feathers. However, the second example is not true. During special revival weeks, we have chapel on days other than Fridays.

The Inverse of a Conditional Statement The inverse of a conditional statement is made by NEGATING THE HYPOTHESIS AND CONCLUSION. Conditional statement: If an animal has feathers, then it is a bird. Inverse: If an animal does NOT have feathers, then it is NOT a bird.

The Contrapositive of a Conditional Statement The contrapositive is formed by NEGATING THE HYPOTHESIS AND CONCLUSION OF THE CONVERSE. Conditional statement: If an animal has feathers, then it is a bird. Converse: If an animal is a bird, then it has feathers. Contrapositive: If an animal is NOT a bird, then it does NOT have feathers.

EQUIVALENT STATEMENTS are statements that are both true or both false A conditional statement An inverse is equivalent to its contrapositive its converse Conditional statement: Inverse: If an animal has feathers, then it is a bird. If an animal does NOT have feathers, Contrapositive: Converse: If an animal is NOT a bird, then it does NOT have feathers. If an animal is a bird, then it has feathers. then it is NOT a bird.

L#2. 1 B Point, Line, & Plane Postulates Remember that we learned in L#1 -3 that postulates are rules that are accepted as true without proof because they are considered to be self-evident statements and are accepted on faith alone. In this lesson, we are going to learn several postulates about points, lines, and planes.

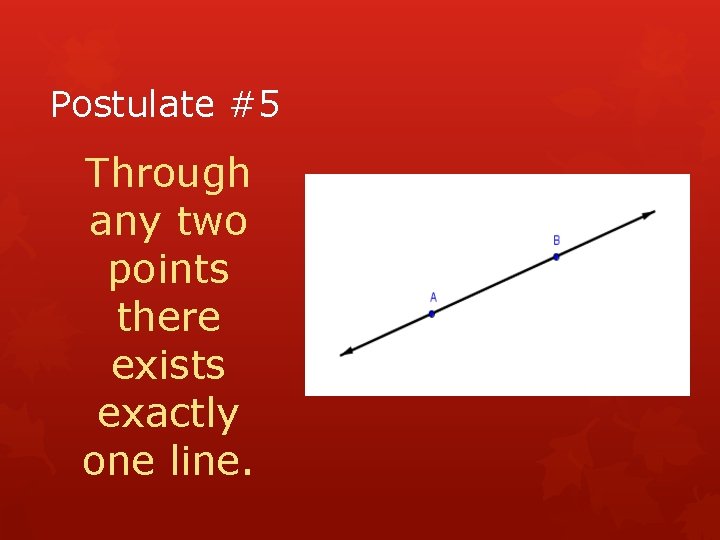
Postulate #5 Through any two points there exists exactly one line.

Postulate #6 A line contains at least two points.

Postulate #7 If two lines intersect, then their intersection is exactly one point.

Postulate #8 Through any three noncollinear points there exists exactly one plane

Postulate #9 A plane contains at least three noncollinear points.

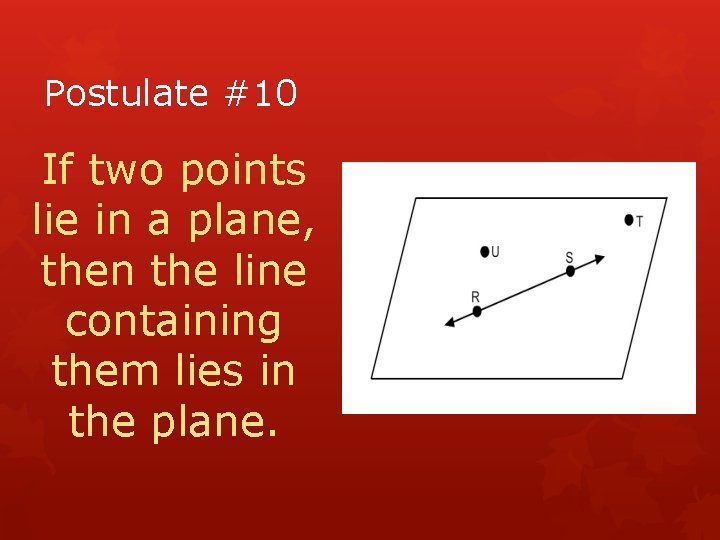
Postulate #10 If two points lie in a plane, then the line containing them lies in the plane.

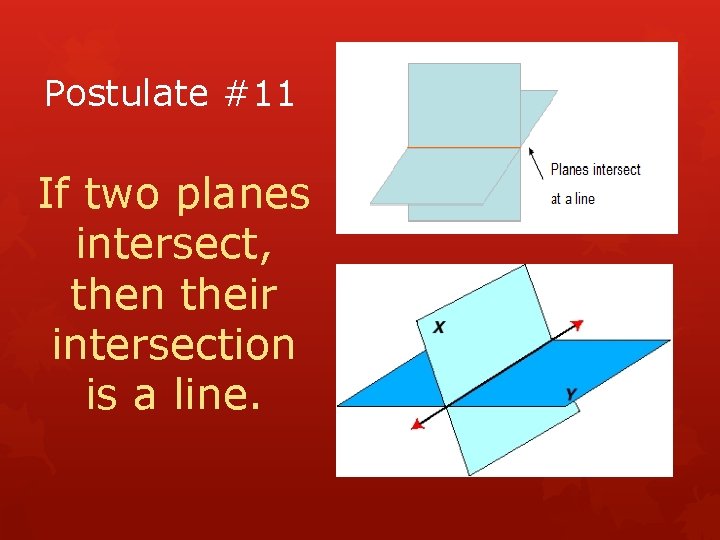
Postulate #11 If two planes intersect, then their intersection is a line.

L#2. 2 Biconditional Statements Recognizing and using definitions 1. A definition uses known words to describe a new word. 2. Definitions can be read forward and backward. 3. All definitions can be written as biconditional statements.

Perpendicular Lines EXAMPLE: Perpendicular lines are two lines which intersect to form a right angle. It is equally correct to say that… “If two lines are perpendicular, then they intersect to form a right angle, ” OR “If two lines intersect to form a right angle, then they are perpendicular. ”

Because the two previous statements can be read forward and backward, both the conditional statement and the converse are true. That means that they can be written as a biconditional statement, statement a statement using the phrase “if and only if. ” The “if and only if” is sometimes abbreviated iff. Two lines are perpendicular if and only if they form right angles. Two lines are perpendicular iff they form right angles.

REVIEW of L#2 -1 and 2 -2 Conditional Statement: If it is noon in Georgia, then it is 9 a. m. in California. Hypothesis: If it is noon in Georgia Conclusion: then it is 9 a. m. in California Converse: If it is 9 a. m. in California, then it is noon in Georgia. Inverse: If it is not noon in Georgia, then it is not 9 a. m. in California. Contrapositive: If it is not 9 a. m. in California, then it is not noon in Georgia. Biconditional: It is noon in Georgia if and only if it is 9 a. m. in California.

REVIEW of L#2 -1 and 2 -2 Conditional Statement: If two circles have the same radius, then they will have the same area. Hypothesis: If two circles have the same radius Conclusion: then they will have the same area Converse: If two circles have the same area, then they have the same radius. Inverse: If two circles do not have the same radius, then they will not have the same area. Contrapositive: If two circles do not have the same area, then they will not have the same radius. Biconditional: Two circles have the same radius if and only if they have the same area.

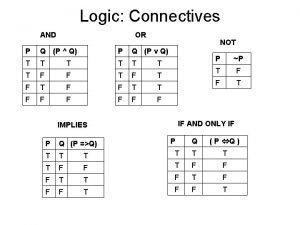
L#2 -3 DEDUCTIVE REASONING Symbolic notation can be used to represent conditional statements. Ø The hypothesis is represented by the letter p. Ø The conclusion is represented by the letter q. Ø A conditional statement can be written symbolically as…

Using the same symbolic notation… Ø The converse can be represented… Ø The inverse can be represented… Ø The contrapositive can be represented…

Using the same symbolic notation… The biconditional statement can be represented… If p, then q, and if q, then p. p if and only if q p iff q

Conditional Statement: If yesterday was Monday, today is Tuesday. Write each statement requested: If yesterday was not Monday, today is not Tuesday. If today is Tuesday, yesterday was Monday. Yesterday was Monday if and only if today is Tuesday.

Deductive Reasoning Deductive reasoning uses *facts *definitions, and *accepted properties in a logical order to write a logical argument. There are 2 laws of deductive reasoning.

Law of Detachment Is this argument valid? Explain. If a player misses a practice the day before a game, he will not be a starting player in the game. Jamal misses practice on Tuesday, so he concludes that he will not start Wednesday’s game.

Law of Syllogism Example of the Law of Syllogism: If a bird is the fastest bird on land, land then it is the largest of all birds. If a bird is the largest of all birds, birds then it is an ostrich What conclusion follows? If a bird is the fastest bird on land, land then it is an ostrich

L#2. 4 Algebraic Properties of Equality Addition Property If equals are added to equals, their sums are equal. If a = b, then a + c = b + c If x = 5, then x + 4 = 5 + 4 Subtraction Property If equals are subtracted from equals, their differences are equal. If a = b, then a – c = b – c If x = 5, then x – 4 = 5 – 4

Algebraic Properties of Equality Multiplication Property If equals multiplied by equals, their products are equal. If a = b, then a (c) = b (c) If x = 5, then x (4) = 5 (4)

Algebraic Properties of Equality Reflexive Property A number equals itself. (Both sides must be identical. ) For any number a, a = a. 30 = 30 Symmetric Property An equation can be written in reverse. If a = b, then b = a. If x = 8, then 8 = x.

Algebraic Properties of Equality

Algebraic Properties of Equality Distributive Property Multiplication can be carried across a plus or minus sign. a(b + c) = ab + ac or a(b – c) = ab – ac 2(x + 5) = 2 x + 10

The algebraic properties are also used in geometry. Reflexive Property Segment Length For any segment AB, AB = AB.

The algebraic properties are also used in geometry. Symmetric Property Segment Length If AB = CD, then CD = AB.

The algebraic properties are also used in geometry. Transitive Property Segment Length If AB = CD and CD = EF, then AB = EF.

Solve the following and justify each step. 2(3 x – 1) = 5 x + 14 Given 6 x – 2 = 5 x + 14 Distributive Property x – 2 = 14 Subtraction Property x = 16 Addition Property

L#2. 5 Proving Statements about Segments Theorem—a true statement that follows as a result of other true statements. All theorems must be proved. Theorems can be proved using 4 types of proofs: *1) 2 -column proof -Numbered statements on the left. -Numbered reasons for each statement on the right. -Presented in a logical order beginning with the given and ending with what you are trying to prove. -The type of proof we will be doing most often this year.

2) Paragraph proof -A proof with the same statements and reasons as above but written in paragraph (complete sentence) form. 3) Flow proof -Has boxes or circles containing statements with reasons underneath using arrows to show the flow of the logical argument. -They may flow down or from left to right.

4) Indirect proof -This proof begins by assuming that the opposite of what you want to prove is true. -Once you show that the opposite is impossible, then you can prove your original statement is true.

*The first three methods above use either the Law of Detachment or the Law of Syllogism. *The fourth method is also called a proof by contradiction. *Your reasons in any type of proof must be a combination of the following: 1) Given 2) Definition 3) Property 4) Postulate 5) Previously proven theorem

Properties of Segment Congruence

L#2. 5 Copying a Segment

5 Reasoning that uses facts, definitions, and accepted properties in a logical way to build a logical argument is ____ reasoning.

26 The _____ Property of Equality says that if I know that 2 quantities are equal, I can replace one with the other in any expression or equation.

31 Solve for x:

35 What construction was learned in Ch #2?

39 A proof that starts off by assuming that the opposite of what you want to prove is true is an _____ proof.

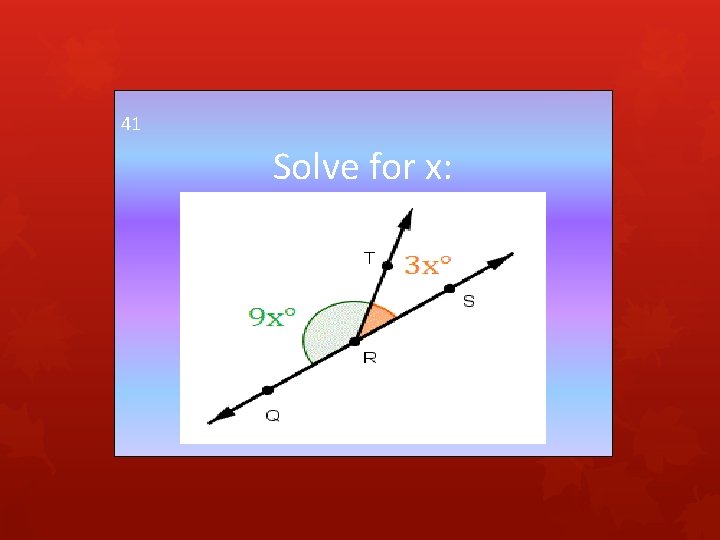
41 Solve for x:

37 If two planes intersect, their intersection is a _____.

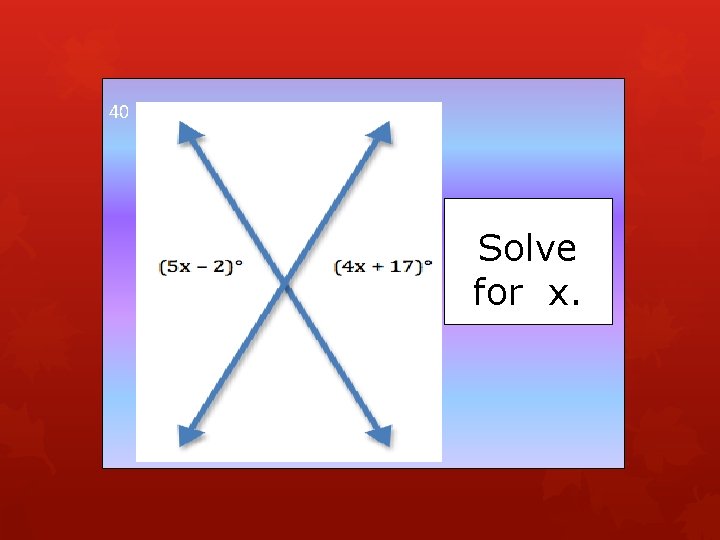
40 Solve for x.

36 A proof with circles or boxes containing statements with reasons underneath and arrows to show to read it is called a ____ proof.

29 An example of the _____ Property of Equality would be “if x + 12 = 40, then x = 28. ”

30 Solve for x:

20 An example of the ____ Property of Equality would be “if x = 2 y, then 3 x = 6 y. ”

6 Every proof’s first statement and reason must be at least one part of the ____.

1 An example of the _______ Property of Equality would be “If AB = 6 and XY = 6, then AB = XY. ”

9 An example of the ____ Property of Equality would be MN = MN.

15 An example of the ___ Property of Equality would be “if x = 25, then x + 10 = 35. ”

17 The ____ is formed by negating the converse.

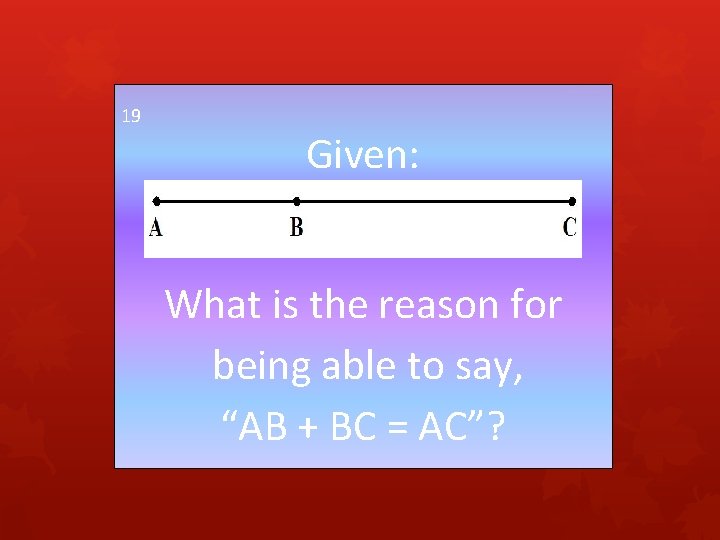
19 Given: What is the reason for being able to say, “AB + BC = AC”?

8 Use the Symmetric Property of Congruence to complete the statement: If xy = 42, then ______.

7 The most common type of proof that we will be doing in class this year is the ___-___ proof.

2 What word means “having the same size and shape”?

22 An example of the ____ Property of Equality would be 5(x + y) = 5 x + 5 y.

28 The Law of ____ means that “If I like red, I will also like blue. If I like blue, I will also like green. Therefore, if I like red, then I will like green. ”

33 If I negate the conditional statement, I will form the _____.

42 If two lines intersect, then their intersection is ___ ___.

38 A proof written in complete sentences in paragraph form is called a ____ proof.

14 The “then” part of a conditional statement is called the ____.

10 Every proof’s last statement must be what you had set out to ____.

21 What phrase is in the middle of every biconditional statement?

4 The “if” portion of a conditional statement is called the ____.