OPENER Pearson PreAP Unit 1 Topic 2 Reasoning

OPENER

Pearson Pre-AP Unit 1 Topic 2: Reasoning and Proof 2 -1: Patterns and Conjectures Pearson Texas Geometry © 2016 Holt Geometry Texas © 2007

TEKS Focus: � (4)(C) Verify that a conjectures is false using a counterexample. � (1)(D) Communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate. � (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. � (1)(E) Create and use representations to organize, record, and communicate mathematical ideas. � (1)(F) Analyze mathematical relationships to connect and communicate mathematical ideas. � (1)(G) Display, explain, or justify mathematical ideas and arguments using precise mathematical language in written or oral communication. � (5)(A) Investigate patterns to make conjectures about geometric relationships, including angles formed by parallel lines cut by a transversal, criteria required for triangle congruence, special segments of triangles, diagonals of quadrilaterals, interior and exterior angles of polygons, and special segments and angles of circles choosing from a variety of tools. �

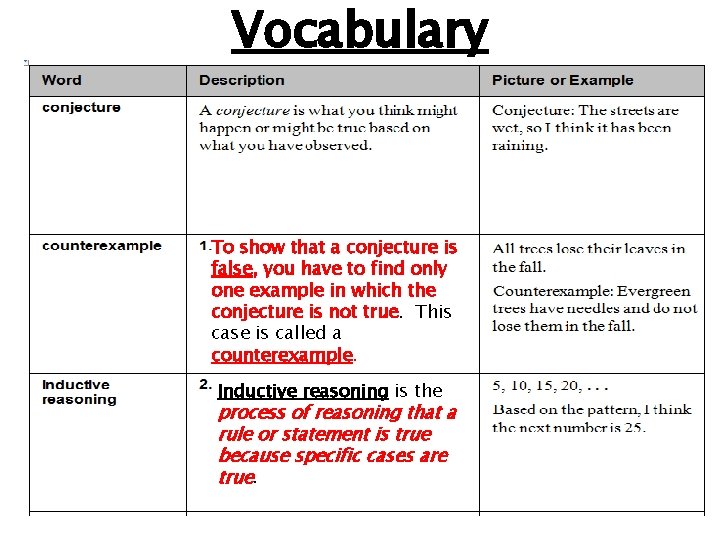
Vocabulary To show that a conjecture is false, you have to find only one example in which the conjecture is not true. This case is called a counterexample. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true.

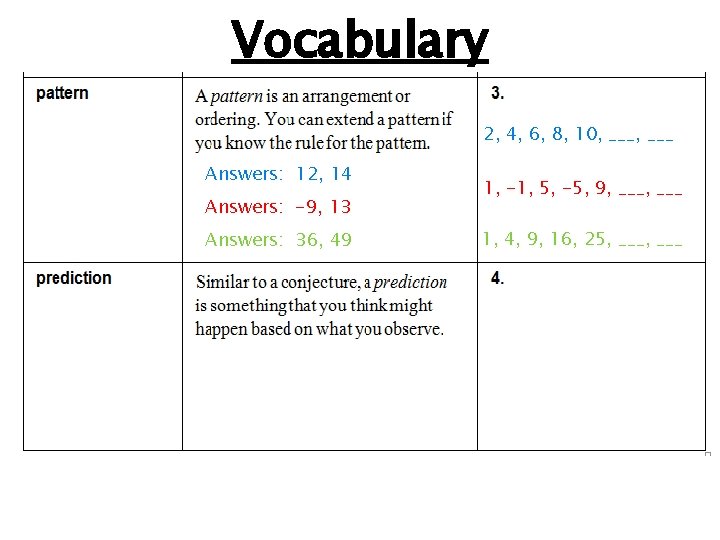
Vocabulary 2, 4, 6, 8, 10, ___ Answers: 12, 14 Answers: -9, 13 Answers: 36, 49 1, -1, 5, -5, 9, ___ 1, 4, 9, 16, 25, ___

Reasoning: Inductive When several examples form a pattern and you assume the pattern will continue, you are applying inductive reasoning. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true.

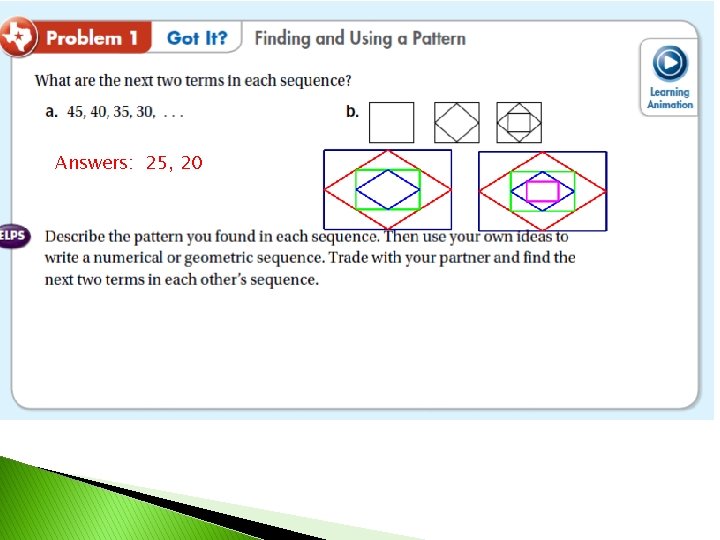
Answers: 25, 20

Reasoning: Inductive You may use inductive reasoning to draw a conclusion from a pattern. A statement you believe to be true based on inductive reasoning is called a conjecture.

Virtual Nerd Videos � What is Inductive Reasoning?

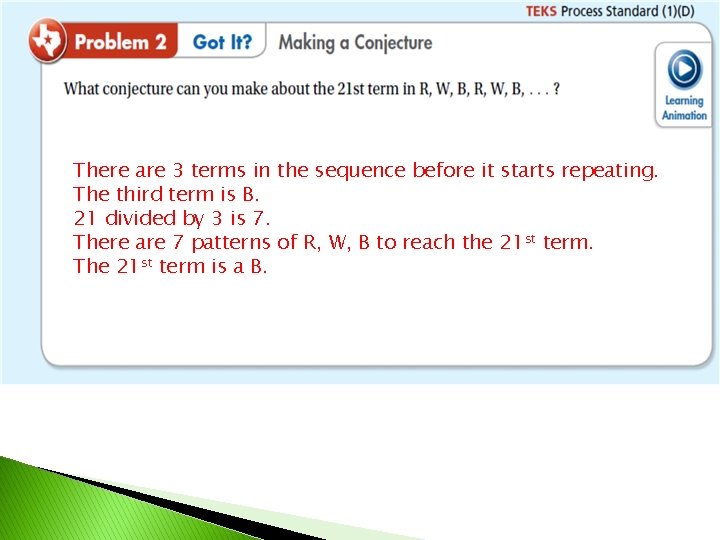
There are 3 terms in the sequence before it starts repeating. The third term is B. 21 divided by 3 is 7. There are 7 patterns of R, W, B to reach the 21 st term. The 21 st term is a B.

1 1 1 = + + + 1 3 3 3 = + + 4 5 5 = + + + 9 7 = 16 7 + 9 = 25 7 + 9 + 11 = 36 Do you notice a pattern developing? Are these sums the squares of the number of terms you are adding? Therefore the sum of the first 30 odd numbers is 30 squared = 900.

The sales are decreasing every month. Draw the line of best fit. Sales in June would be approximately 7500 backpacks. Since August is usually when school supplies are bought for the next school year, we can expect the number of backpacks sold to significantly increase. So no, we should not use this graph to predict sales in August.

Practice Complete the conjecture. The sum of two positive numbers is ? . List some examples and look for a pattern. 1+1=2 3. 14 + 0. 01 = 3. 15 3, 900 + 1, 000, 017 = 1, 003, 917 The sum of two positive numbers is positive.

To show that a conjecture is always true, you must prove it. To show that a conjecture is false, you have to find only one example in which the conjecture is not true. This case is called a counterexample. A counterexample can be a drawing, a statement, or a number. Inductive Reasoning 1. Look for a pattern. 2. Make a conjecture. 3. Prove the conjecture or find a counterexample.

Problem 5 Show that the conjecture is false by finding a counterexample. For every integer n, n 3 is positive. Pick integers and substitute them into the expression to see if the conjecture holds. Let n = 1. Since n 3 = 1 and 1 > 0, the conjecture holds. Let n = – 3. Since n 3 = – 27 and – 27 0, the conjecture is false. n = – 3 is a counterexample.

Problem 6 A red flower could be a tulip or a carnation or other types of flowers. If three points are collinear, there an infinite number of planes that would pass through three points. 3 times 5 = 15, and 15 is not divisible by 6.

Not in your notes: Show that the conjecture is false by finding a counterexample. The radius of every planet in the solar system is less than 50, 000 km. Planets’ Diameters (km) Mercury Venus Earth Mars 4880 12, 100 12, 800 6790 Jupiter Saturn Uranus Neptune Pluto 143, 000 121, 000 51, 100 49, 500 2300 Since the radius is half the diameter, the radius of Jupiter is 71, 500 km and the radius of Saturn is 60, 500 km. The conjecture is false.

Not in your notes: Show that the conjecture is false by finding a counterexample. For any real number x, x 2 ≥ x. Let x = Since 1. 2 1 2 2 1 = 4, 1 4 The conjecture is false. 1 ≥ 2.

Not in your notes: Show that the conjecture is false by finding a counterexample. Two complementary angles are not congruent. 45° + 45° = 90° If the two congruent angles both measure 45°, the conjecture is false.