Geometry Chapter 9 Review Secant A line that

Geometry Chapter 9 Review

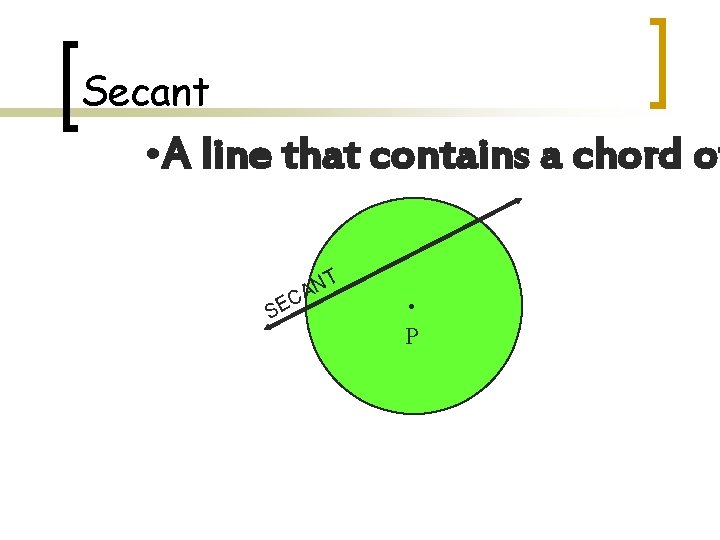
Secant • A line that contains a chord of SE NT A C . P

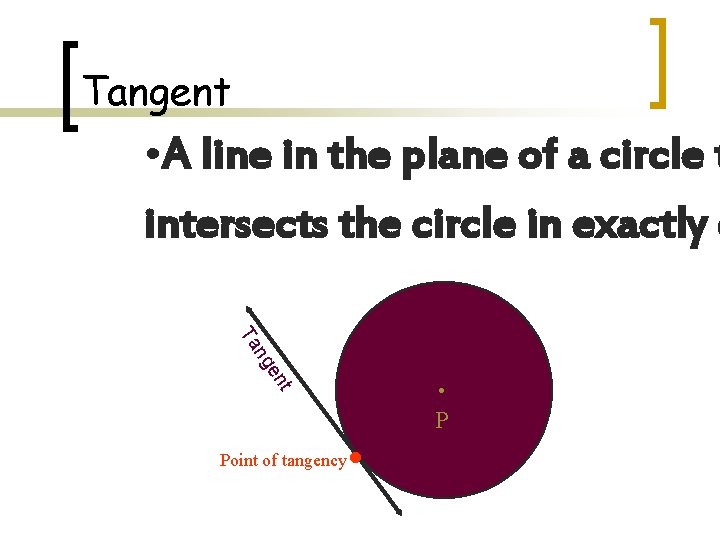
Tangent • A line in the plane of a circle t intersects the circle in exactly o nt ge n Ta . Point of tangency . P

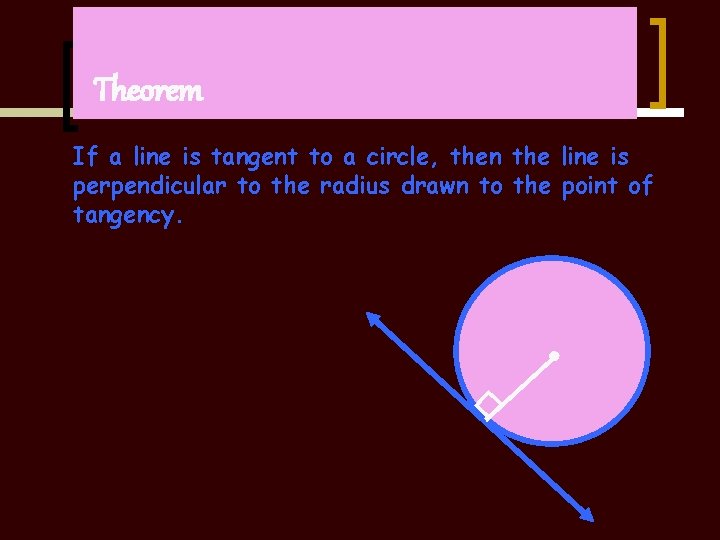
Theorem If a line is tangent to a circle, then the line is perpendicular to the radius drawn to the point of tangency. ●

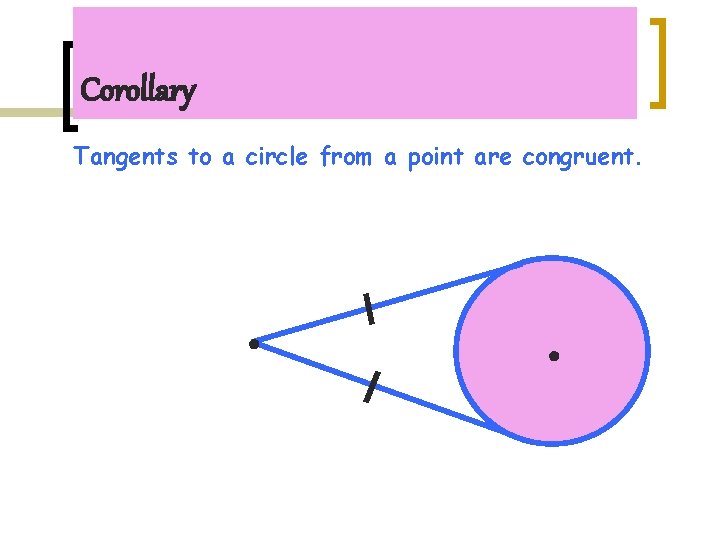
Corollary Tangents to a circle from a point are congruent. ● ●

Theorem • In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent. J M 22 ~ LM. If m 1 = m 2, then JK = 7 7 ~ LM, then m 1 = m 2. If JK = 11 m K k 7 7

Theorem In the same circle or in congruent circles: • congruent arcs have congruent chords • congruent chords have congruent arcs ● O

Theorem A diameter that is perpendicular to a chord bisects the chord and its arc. ● O

Theorem In the same circle or in congruent circles: • chords equally distant from the center (or centers) are congruent • congruent chords are equally distant from the center (or centers) ● O

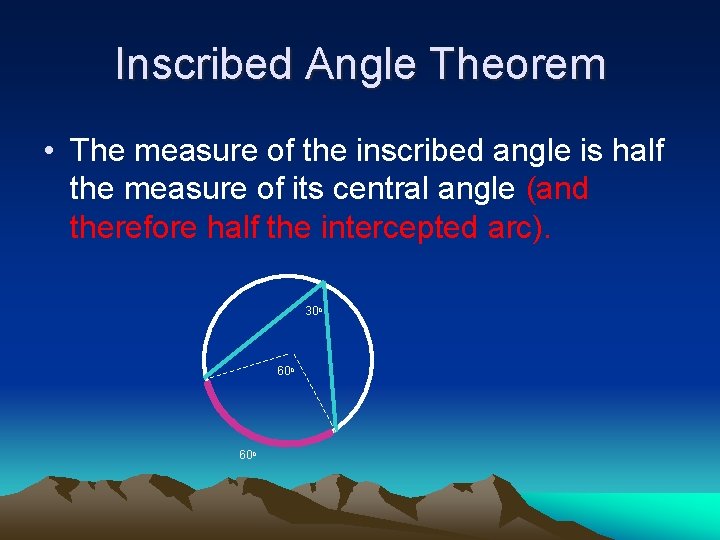
Inscribed Angle Theorem • The measure of the inscribed angle is half the measure of its central angle (and therefore half the intercepted arc). 30 o 60 o

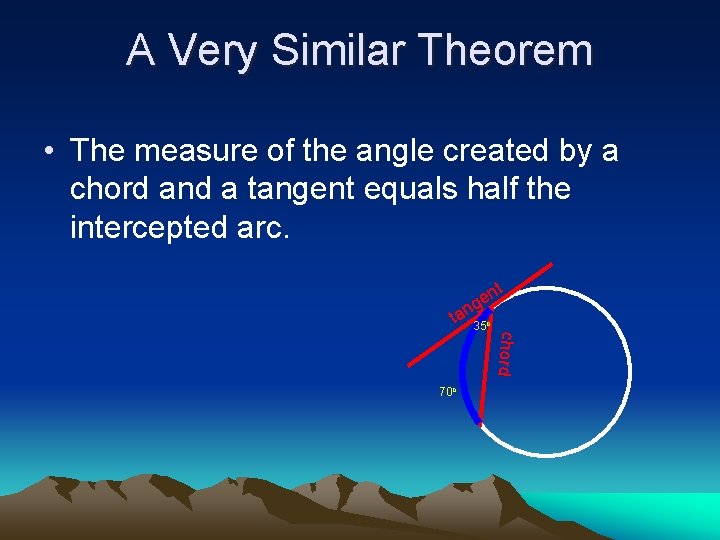
A Very Similar Theorem • The measure of the angle created by a chord and a tangent equals half the intercepted arc. chord nt e g n a t 35 o 70 o

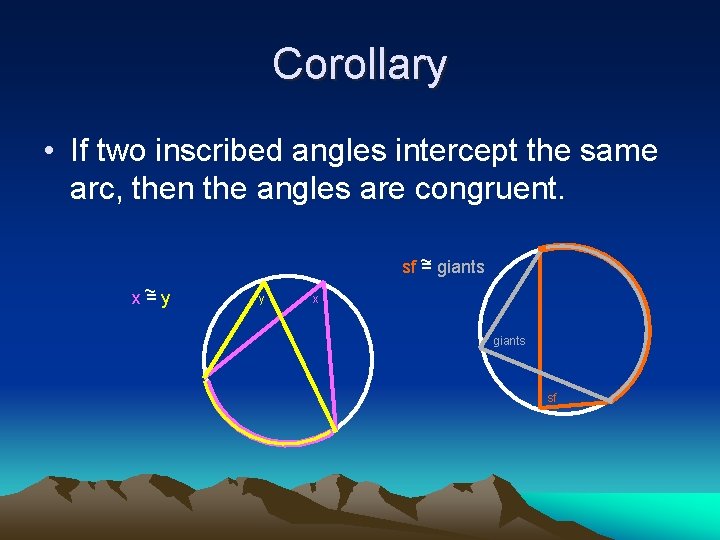
Corollary • If two inscribed angles intercept the same arc, then the angles are congruent. ~ giants sf = x~ =y y x giants sf

Corollary • If an inscribed angle intercepts a semicircle, then it is a right angle. Why? 180 o eter diam 90 o

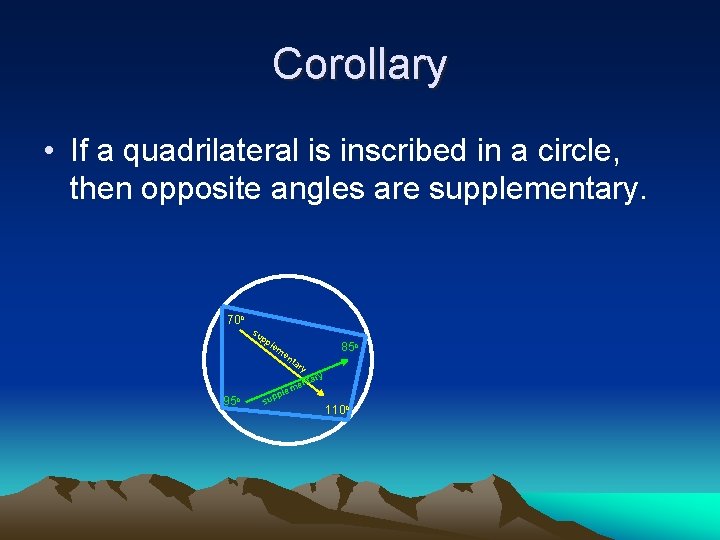
Corollary • If a quadrilateral is inscribed in a circle, then opposite angles are supplementary. 70 o su pp lem 85 o en ta 95 o ry ary nt me ple sup 110 o

Interior Angle Theorem The measure of an angle formed by two chords that intersect inside a circle is equal to half the sum of the measures of the intercepted arcs. A 1 50˚ D B 60˚ m<1 = ½( m. AD + m. BC ) C If m. AD = 50 and m. BC = 60 55 m<1 = ½(50 + 60) = _____

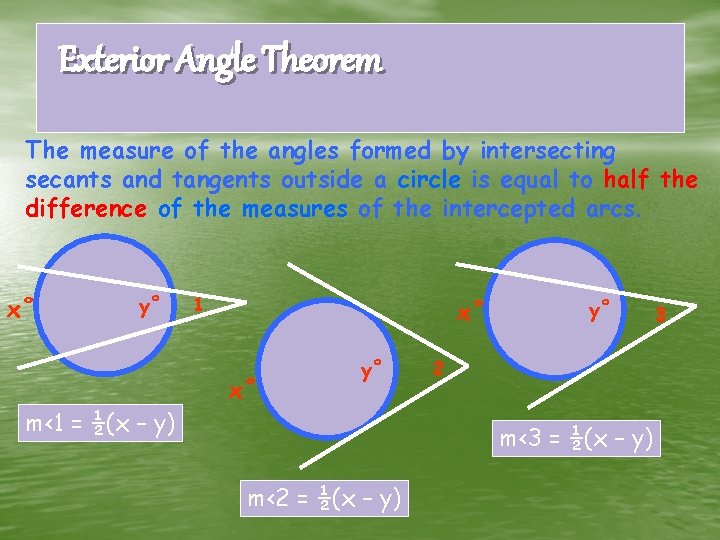
Exterior Angle Theorem The measure of the angles formed by intersecting secants and tangents outside a circle is equal to half the difference of the measures of the intercepted arcs. x˚ y˚ m<1 = ½(x – y) 1 x˚ x˚ y˚ y˚ 2 m<3 = ½(x – y) m<2 = ½(x – y) 3

Theorem • When two chords intersect inside a circle, the product of the segments of one chord equals the product of the segments of the Q S other chord. 4 8 8 x 3=6 x 4 P x. X 3 6 R

Theorem • When two secant segments are drawn to a circle from an external point, the product of one secant segment and its external segment equals the product of the other secant segment and its external segment. FD x FE = FH x FG E D G H External x Whole Thing = External x Whole Thing F

Theorem • When a secant segment and a tangent segment are drawn to a circle from an external point, the product of the secant segment and its external segment is equal to the square of the tangent segment. A PB x PC = (PA)2 P C External x Whole Thing = (Tangent)2 B

HW: Start After You Finish the Ch. 8 Quiz • Chapter 9 W. S.