Postulates and Paragraph Proofs Eric Hoffman Advanced Geometry

Postulates and Paragraph Proofs Eric Hoffman Advanced Geometry PLHS Oct. 2007

Key Topics • Postulate or Axiom: a statement that describes a fundamental relationship between basic terms in Geometry – Ex. Through any two points there is exactly one line – Ex. The shortest distance between any two points is a line • These statements are always accepted as true

Key Topics • These are essential in writing proofs for this chapter

Using Postulates • Determine whether each statement is always, sometimes, or never true using our knowledge about postulates. • If plane T contains and then plane T contains point G • For , if X lies in plane Q and Y lies in plane R then, plane Q intersects plane R • contains three non-collinear points

Key Topics • Theorem: a statement or postulate that has been shown to be true • Once proven true, a theorem can be used like a statement or postulate to justify that other statements are true

Key Topics • Proof: a logical argument in which each statement you make is supported by a statement that is accepted as true (can be a axiom, postulate, theorem) • Paragraph Proof: a type of proof in which you write a paragraph to explain why a conjecture is true for a given situation

All paragraph proofs should start with what is given and what we want to prove Proofs should end with a box which denotes the end of your proof

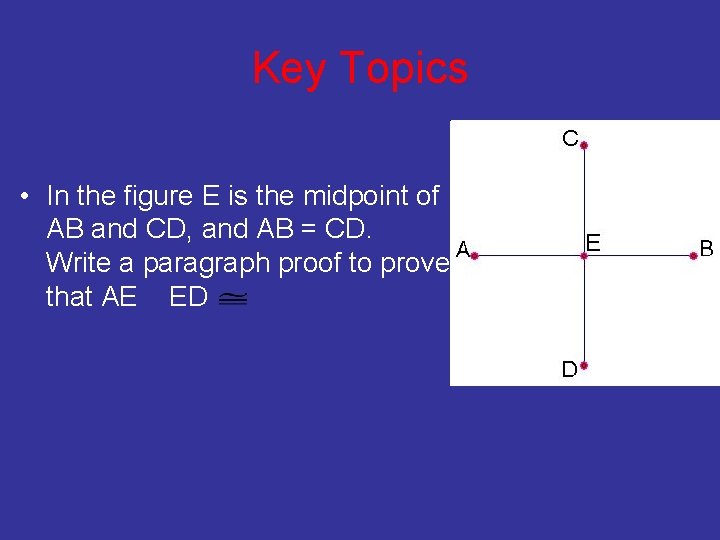
Key Topics • In the figure E is the midpoint of AB and CD, and AB = CD. Write a paragraph proof to prove that AE ED

Key Topics • Given: E is the midpoint of AB and CD, and AB = CD • Prove: AE ED Proof: Since E is the midpoint of AB by the Midpoint Theorem we know that AE EB, similarly we know that CE ED. By the definition of congruent segments we know that AE = EB = ½ AB, similarly we also know that CE = ED = ½ CD. Since we know that AB = CD, by the multiplication property we can say that ½ AB = ½ CD, and thus AE = ED. Therefore by the definition of congruent segments AE ED □

Key Topics • Homework pg. 91, 92 10 – 30 even 11 problems!!