REASONING Deductive reasoning syllogisms Reasoning Syllogisms are examples

REASONING Deductive reasoning - syllogisms

Reasoning Syllogisms are examples of gaining knowledge by reasoning. Can you discuss in your groups the benefits of gaining knowledge by this way?

Rationalism Rationalists believe that reason is the most important source of knowledge because it seems to give us some certainty.

The curious incident An expensive racehorse has been stolen. A policeman talks to Sherlock Holmes. I’ve been stolen, that’s why I’ve got such a long face!

The curious incident Does any aspect of the crime strike you as significant Mr Holmes? Yes constable, the curious incident of the dog in the night.

The curious incident The dog did nothing in the night Sir. That is the curious incident!

Who stole the horse?

Holmes’ reasoning The solution to the crime hinges on the fact that the guard dog did not bark in the night, and from this Holmes deduces that the thief must have been known to the dog. I know him!

Holmes’ reasoning can be laid out as follows • Guard dogs bark at strangers • The guard dog did not bark at the thief • Therefore thief was not a stranger

Deductive and induction reasoning

Deductive reasoning

Syllogisms Holmes’s reasoning is an example of a syllogism.

The Socrates Syllogism premises • All human beings are mortal • Socrates is a human being • Therefore Socrates is mortal Rationalism – A branch of philosophy which takes reason as the most important source of knowledge conclusion

Syllogisms contain: • Two premises and a conclusion • Three terms, each must occur twice (“Socrates”, “human”, “mortal”. ) • Quantifiers, such as “all”, or “some” or “no” which tell us of the quantity being referred to. “TOK for the IB Diploma”, Richard van de Lagemaat, Cambridge

Another example • All boys like to fart • Chris is a boy • Chris likes to fart!

Truth and validity An argument is valid if the conclusion follows logically from the premises. All hippopotamuses eat cockroaches Dave is a hippopotamus Therefore Dave eats cockroaches Imagine that some strange planet exists where the premises are true Both premises and conclusion are false, but the argument is valid.

Truth and validity All rats are teachers Mr Jackson is a rat Therefore Mr Jackson is a teacher Both premises are false and conclusion is true! (but the argument is still valid).

Deductive reasoning and truth For an argument to be true you must be able to answer “yes” to the following questions: • Are the premises true? • Is the argument valid?

Socrates is a man All men are mortal Therefore Socrates is mortal The conclusion is only true if the premises are true.

Make up your own VALID syllogisms to illustrate each of the following; 1. 2 true premises and a true conclusion 2. 1 true premise, 1 false premise and a true conclusion 3. 1 true premise, 1 false premise and a false conclusion 4. 2 false premises and a true conclusion 5. 2 false premises and a false conclusion

Deciding whether a syllogism is valid Trying to decide if a syllogism is valid is not easy. Venn diagrams can help (at last a good use for Venn diagrams!)

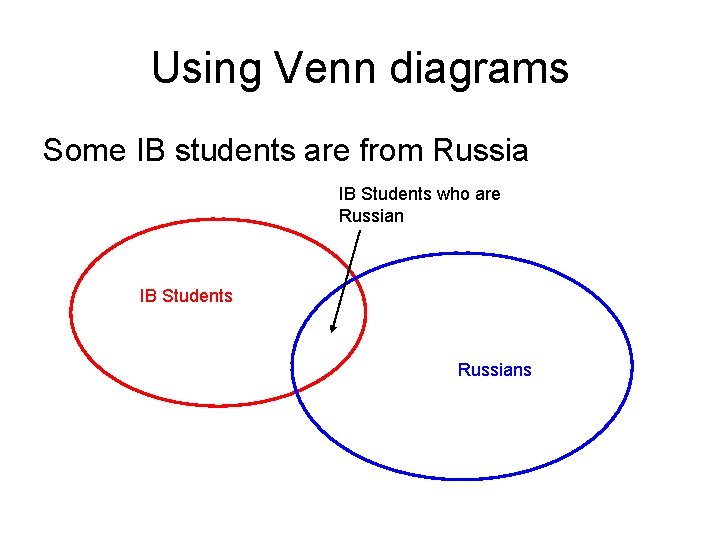
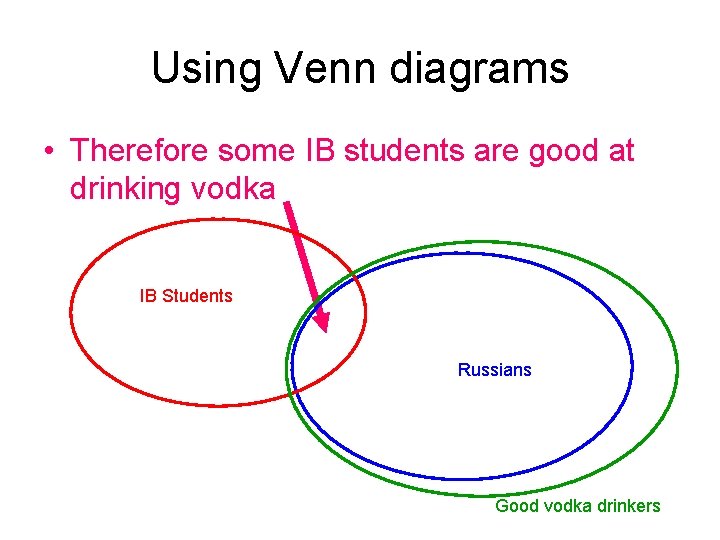
Deciding whether a syllogism is valid Mmmmmm …Vodka! • Some IB students are from Russia • All Russians are good at drinking vodka • Therefore some IB students are good at drinking vodka Is this a valid argument? IB students from Oslo International School

Using Venn diagrams Some IB students are from Russia IB Students who are Russian IB Students Russians

Using Venn diagrams All Russians are good at drinking vodka IB Students Russians Good vodka drinkers

Using Venn diagrams • Therefore some IB students are good at drinking vodka IB Students Russians Good vodka drinkers

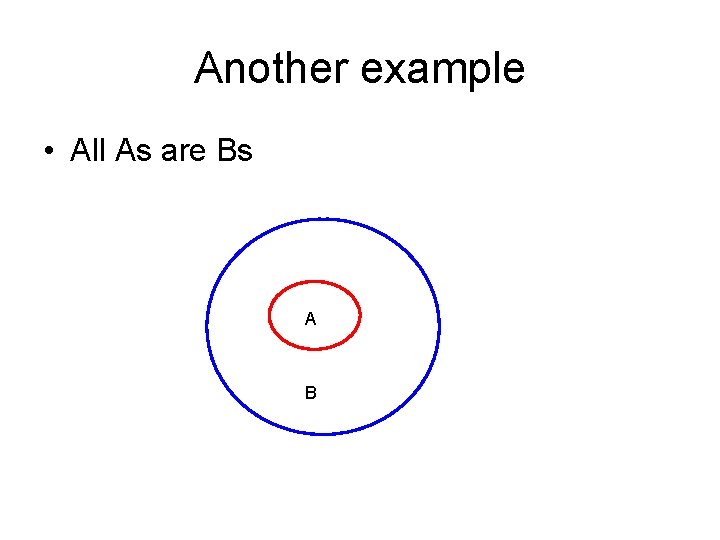
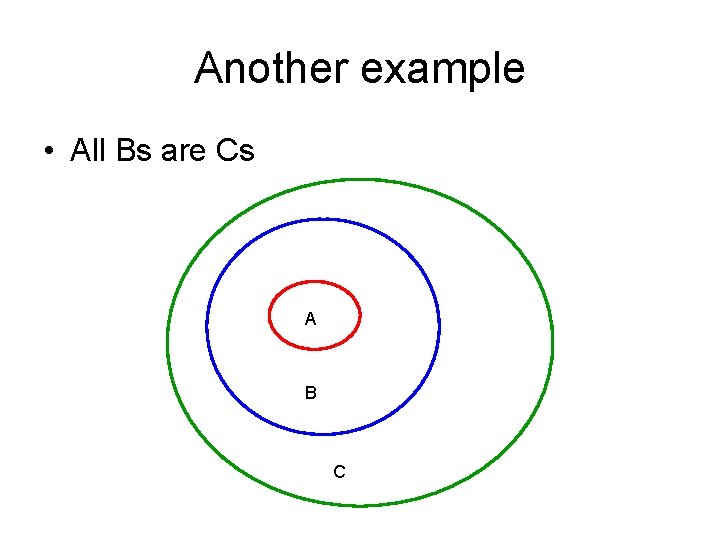
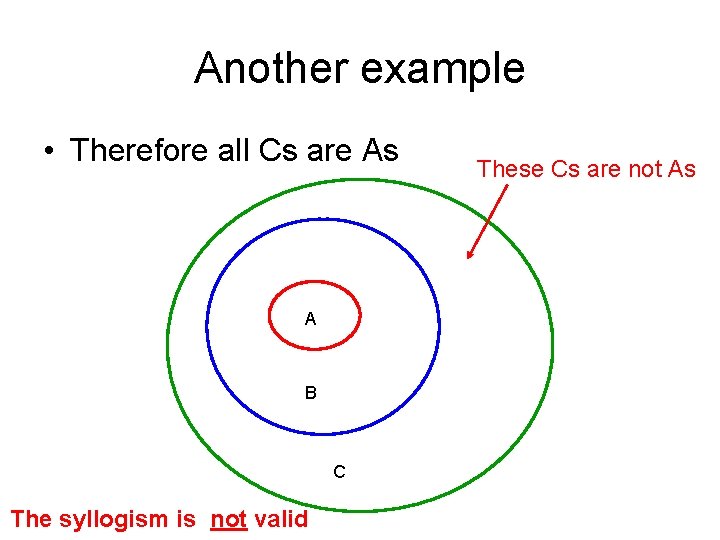
Another example • All As are Bs • All Bs are Cs • Therefore all Cs are As

Another example • All As are Bs A B

Another example • All Bs are Cs A B C

Another example • Therefore all Cs are As A B C The syllogism is not valid These Cs are not As

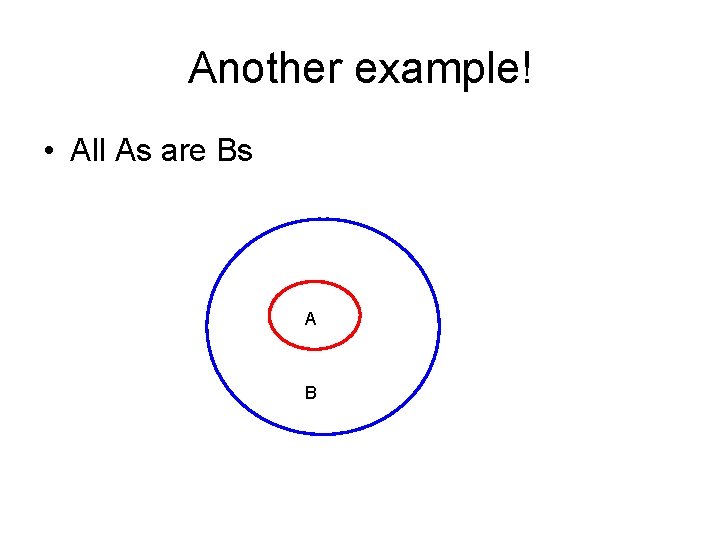
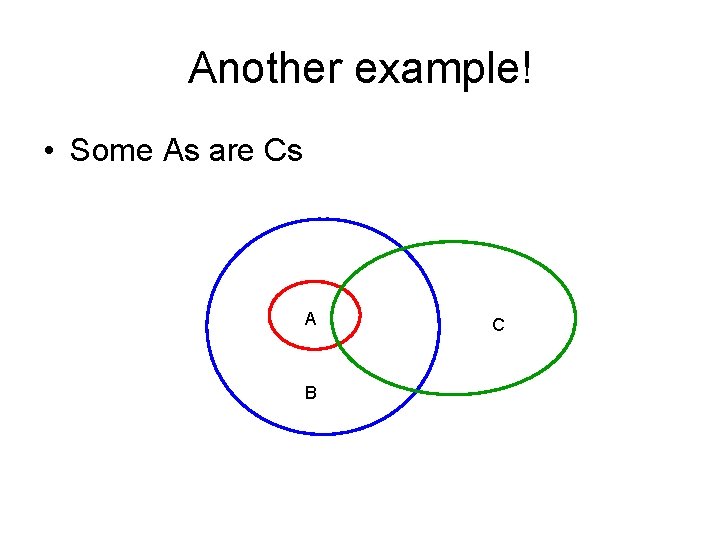
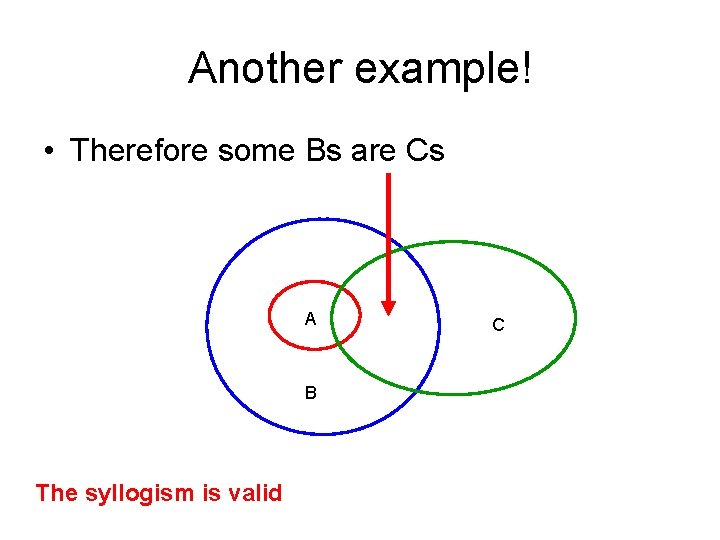
Another example! • All As are Bs • Some As are Cs • Therefore some Bs are Cs

Another example! • All As are Bs A B

Another example! • Some As are Cs A B C

Another example! • Therefore some Bs are Cs A B The syllogism is valid C

Now your turn Using Venn diagrams in your notebooks, decide whether each of the following arguments is valid or invalid. Also decide if the conclusion is true. Remember that to be true the two premises must be true and the argument must be valid.

Valid or invalid • All Norwegians eat hotdogs • Marek eats hotdogs • Therefore Marek is Norwegian

Valid or invalid • All Year 12 boys are brave • Some brave people are compassionate • Some Year 12 boys are compassionate

Valid or invalid • Some physicists are frauds • Some frauds are not wealthy • Therefore some physicists are not wealthy

Valid or invalid • All Polish people have dogs • No good football players have dogs • Therefore no Polish people are good football players

Valid or invalid • All clever girls are redheaded • All red heads are rich • Therefore all clever girls are rich