Inductive Reasoning Deductive Reasoning and False Premise LOGIC

Inductive Reasoning, Deductive Reasoning, and False Premise LOGIC

HOW WOULD YOU GO ABOUT SOLVING THIS CASE? “There has been a murder done, and the murderer was a man. He was more than 6 feet high, was in the prime of life, had small feet for his height, wore coarse, square-toed boots and smoked a Trichinopoly cigar. ” –Doyle

PROBLEM SOLVING � Logic – The science of correct reasoning. � Reasoning – The drawing of inferences or conclusions from known or assumed facts. When solving a problem, one must understand the question, gather all pertinent facts, analyze the problem i. e. compare with previous problems (note similarities and differences), perhaps use pictures or formulas to solve the problem.

ARGUMENTS � An argument is a series of statements, one of which is offered as a statement to be supported, and the rest of which are offered as support. � A conclusion is a statement to be supported. � A premise is a statement that offers support.

PREMISES � Major Premise: contains the major term All bird feathers are light. � Minor Premise: contains the minor term Parrot is a bird.

PREMISES � Major Premise: All bird feathers are light. � Minor Premise: Parrot is a bird. � Conclusion: Hence, parrots have light feathers.

IDENTIFY THE MAJOR AND MINOR PREMISES Every triangle has three sides. The figure drawn here is a triangle. So, the figure drawn here is a triangle and has three sides. Earth is a planet. All planets revolve around the sun. Therefore, earth revolves around the sun.

IDENTIFY THE MAJOR AND MINOR PREMISES To get a degree, one must have 120 credits. John has 130 credits. Hence, John has a degree. I am a man. All men must die. Therefore, I must die.

DEDUCTIVE REASONING � Deductive Reasoning – A type of logic in which one goes from a general statement to a specific instance. � The classic example All men are mortal. (major premise) Socrates is a man. (minor premise) Therefore, Socrates is mortal. (conclusion)

DEDUCTIVE REASONING Examples: All students eat pizza. Claire is a student at ASU. Therefore, Claire eats pizza. All athletes work out in the gym. Barry Bonds is an athlete. Therefore, Barry Bonds works out in the gym.

DEDUCTIVE REASONING All math teachers are over 7 feet tall. Mr. D. is a math teacher. Therefore, Mr. D is over 7 feet tall. � The argument is valid, but is certainly not true. � The above examples are of the form If p, then q. (major premise) x is p. (minor premise) Therefore, x is q. (conclusion)

DEDUCTIVE REASONING � Syllogism: An argument composed of two statements or premises (the major and minor premises), followed by a conclusion. All men are mortal. (major premise) Socrates is a man. (minor premise) Therefore, Socrates is mortal. (conclusion) The above is an example of a syllogism.

DEDUCTIVE REASONING What does valid mean? � What does invalid mean? � For any given set of premises, if the conclusion is guaranteed, the arguments is said to be valid. � If the conclusion is not guaranteed (at least one instance in which the conclusion does not follow), the argument is said to be invalid. � BE CARFEUL, DO NOT CONFUSE TRUTH WITH VALIDITY! �

VALIDITY In other words: � A valid argument is one in which it is impossible for the premises to be true while the conclusion is false—i. e. , if the premises are true, then the conclusion must be true as well. � An invalid argument is one in which it is possible for the premises to be true while the conclusion is false.

FALLACY � A fallacy is an error in the reasoning process whereby the connection between the premises and the conclusion is not what has been claimed. � False premise: statement that is false

FALSE PREMISES � False premises: Mickey mouse is a cat All cats have 7 legs False Conclusion: Mickey mouse has 7 legs Valid Conclusion

FALSE PREMISES (1) All San Franciscans are seven feet tall (2) Jean Jones is a San Franciscan. (3) (Therefore) Jean Jones is seven feet tall. Valid Conclusion

FALSE PREMISES (1) All men are morta. L (2) Socrates is a man. (3) (Therefore) Jean Jones is seven feet tall. Invalid Conclusion

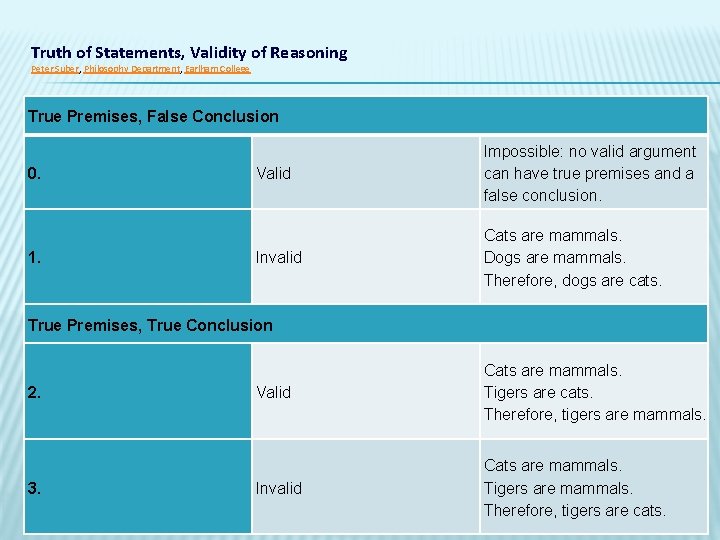
Truth of Statements, Validity of Reasoning Peter Suber, Philosophy Department, Earlham College True Premises, False Conclusion 0. 1. Valid Impossible: no valid argument can have true premises and a false conclusion. Invalid Cats are mammals. Dogs are mammals. Therefore, dogs are cats. True Premises, True Conclusion 2. 3. Valid Cats are mammals. Tigers are cats. Therefore, tigers are mammals. Invalid Cats are mammals. Tigers are mammals. Therefore, tigers are cats.

Truth of Statements, Validity of Reasoning False Premises, False Conclusion 4. 5. Valid Dogs are cats. Cats are birds. Therefore, dogs are birds. Invalid Cats are birds. Dogs are birds. Therefore, dogs are cats. False Premises, True Conclusion 6. 7. Valid Cats are birds. Birds are mammals. Therefore, cats are mammals. Invalid Cats are birds. Tigers are birds. Therefore, tigers are cats.

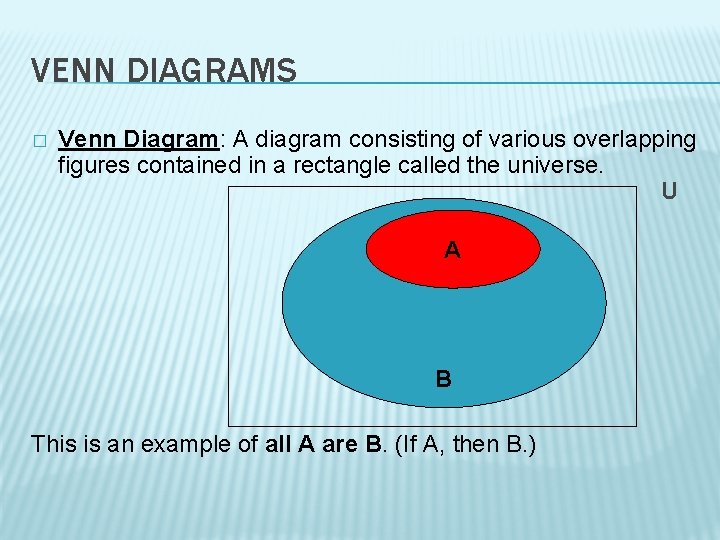
VENN DIAGRAMS � Venn Diagram: A diagram consisting of various overlapping figures contained in a rectangle called the universe. U A B This is an example of all A are B. (If A, then B. )

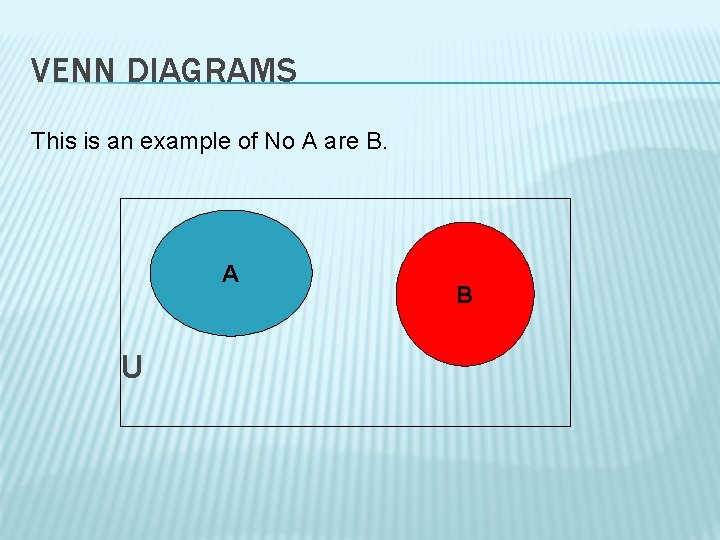
VENN DIAGRAMS This is an example of No A are B. A U B

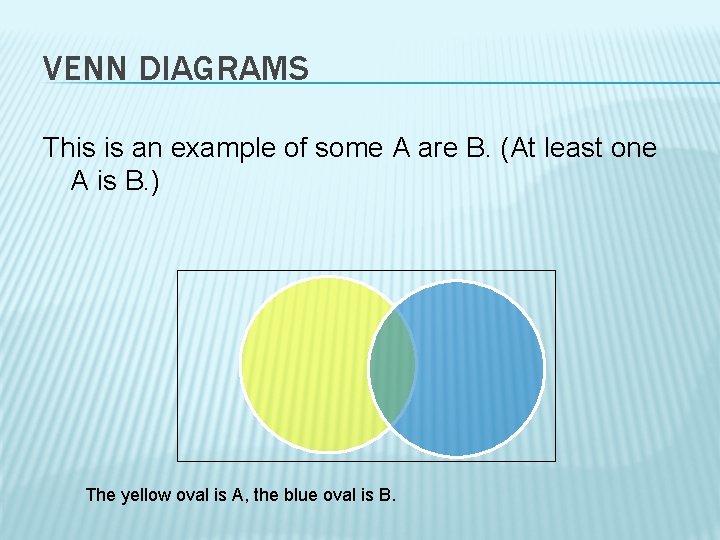
VENN DIAGRAMS This is an example of some A are B. (At least one A is B. ) The yellow oval is A, the blue oval is B.

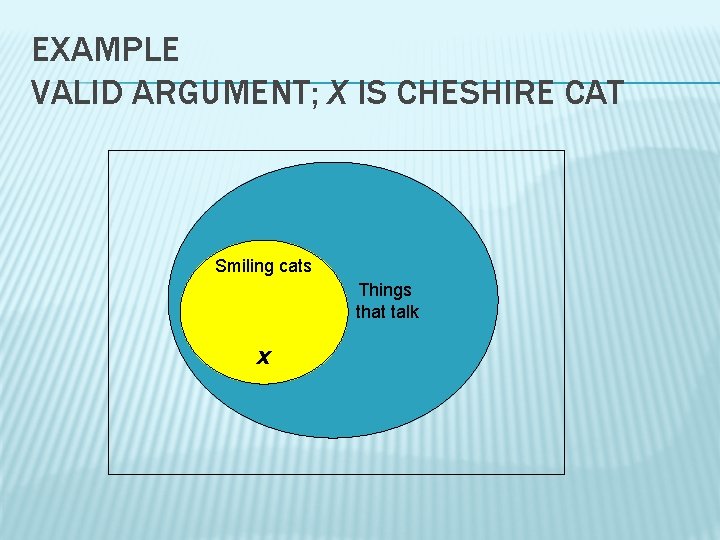
EXAMPLE � Construct a Venn Diagram to determine the validity of the given argument. All smiling cats talk. The Cheshire Cat smiles. Therefore, the Cheshire Cat talks. VALID OR INVALID? ? ?

EXAMPLE VALID ARGUMENT; X IS CHESHIRE CAT Smiling cats Things that talk x

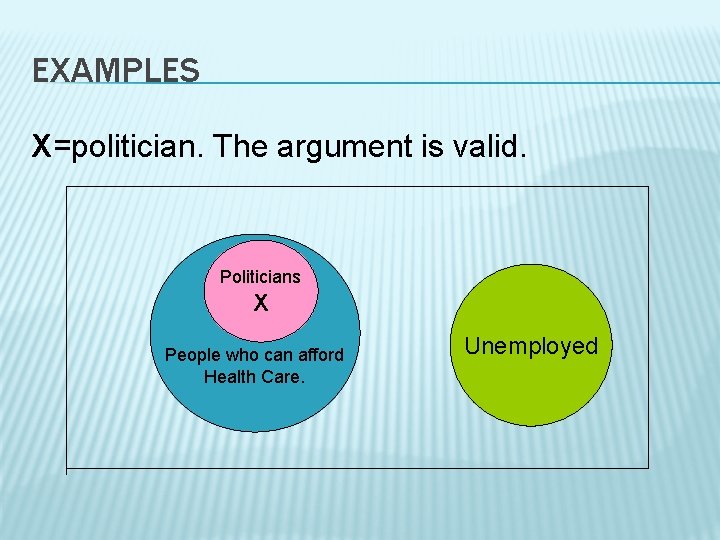
EXAMPLES � No one who can afford health insurance is unemployed. All politicians can afford health insurance. Therefore, no politician is unemployed. VALID OR INVALID? ? ?

EXAMPLES X=politician. The argument is valid. Politicians X People who can afford Health Care. Unemployed

EXAMPLE Some professors wear glasses. Mr. Einstein wears glasses. Therefore, Mr. Einstein is a professor. Let the yellow oval be professors, and the blue oval be glass wearers. Then x (Mr. Einstein) is in the blue oval, but not in the overlapping region. � Is the argument valid or invalid? The argument is invalid.

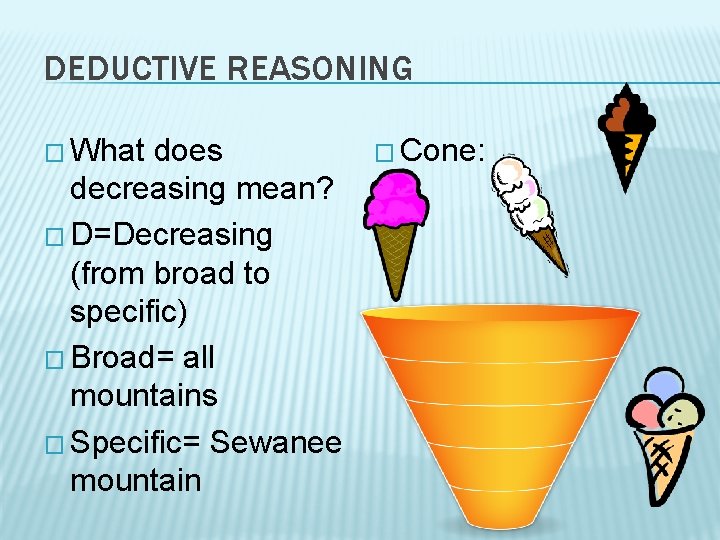
DEDUCTIVE REASONING � What does decreasing mean? � D=Decreasing (from broad to specific) � Broad= all mountains � Specific= Sewanee mountain � Cone:

INDUCTIVE REASONING Inductive Reasoning, involves going from a series of specific cases to a general statement. The conclusion in an inductive argument is never guaranteed. Example: What is the next number in the sequence 6, 13, 20, 27, … There is more than one correct answer.

INDUCTIVE REASONING Here’s the sequence again 6, 13, 20, 27, … � Look at the difference of each term. � 13 – 6 = 7, 20 – 13 = 7, 27 – 20 = 7 � Thus the next term is 34, because 34 – 27 = 7. � However what if the sequence represents the dates. Then the next number could be 3 (31 days in a month). � The next number could be 4 (30 day month) � Or it could be 5 (29 day month – Feb. Leap year) � Or even 6 (28 day month – Feb. ) �

INDUCTIVE What does Increasing mean? � I= Increasing (from specific to broad) � Specific- I love The Hunger Games. � Broad- I love all movies � � Volcano/ Mountain

DEDUCTIVE VS. INDUCTIVE � Deductive reasoning is the process of reasoning from known facts to conclusions. When you reason deductively, you can say “therefore” with certainty. If your facts were firm to begin with, then your conclusions will also be firm. � Example Known Fact: The cut-off date for swim camp registration is June 15. After that date, kids go on a wait list - no exceptions allowed. Known Fact: You have missed the cut-off to date to register your child by two days. Conclusion: Your child won’t be registered and her name will go on the wait list.

DEDUCTIVE VS. INDUCTIVE � Inductive reasoning is the process of going from observations to conclusions. This type of conclusion is sometimes called an inference. Successful inductive reasoning depends on the quality of your observations, or evidence. � Example Observation: Tonya is seen walking from her car to her home with a set of golf clubs. Observation: Tonya’s husband Jeff loves golf and tomorrow is his birthday. Conclusion (inference): Tonya has bought the set of golf clubs for Jack.

DEDUCTIVE VS. INDUCTIVE � Can you see the difference? � Deductive reasoning drives you to a conclusion based on known facts. Inductive reasoning depends on human observation. Tonya, after all, may be borrowing the golf clubs. Or she may have taken up golf herself! You wouldn’t know unless you observed carefully, and even then, you would have to describe your conclusion as “probable” but not firm.

DEDUCTIVE VS. INDUCTIVE This risk of uncertainty in inductive reasoning is why crime scene investigators must ensure that they have gathered many observations (evidence) before drawing a conclusion. � However, here’s something interesting. Once CSI’s have biological evidence of a person at the scene, they can switch back to deductive reasoning. If it is a known fact that someone’s fingerprints or DNA identify him or her, then it can be deduced that fingerprint or DNA evidence at the scene proves the person was there. � So that’s it. Deductive and inductive. It takes both types of reasoning help us move around this world. �

DEDUCTIVE OR INDUCTIVE? 1) 2) major premise: All tortoises are vegetarians � minor premise: Bessie is a tortoise � conclusion: Therefore, Bessie is a vegetarian � � Deductive Boss to employee: “Biff has a tattoo of an anchor on his arm. He probably served in the Navy. ” Inductive

Do the following use inductive or deductive reasoning (write “I” for inductive and “D” for deductive: � ____ 3. All cats have fur. � Xena is a cat. � Therefore, Xena has fur. � ____ 4. Some horses are big. � All horses have tails. � Therefore, anything with a tail is big. � ____ 5. All humans have a nose. � Bobby is human. � Therefore, Bobby has a nose. �

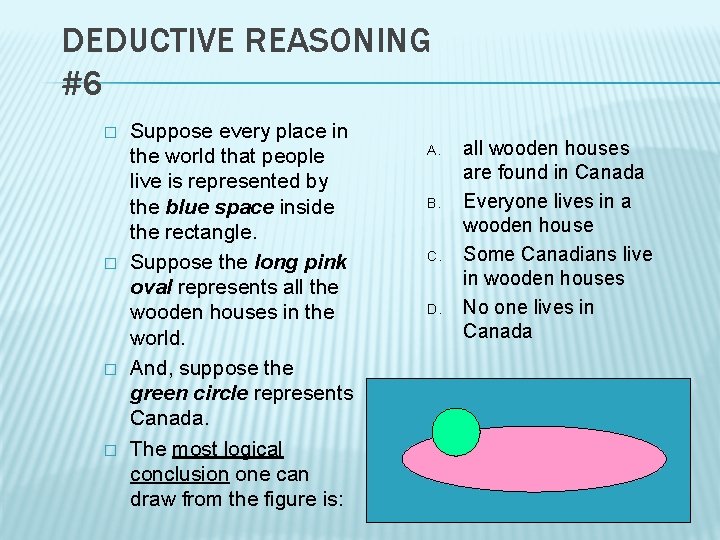
DEDUCTIVE REASONING #6 � � Suppose every place in the world that people live is represented by the blue space inside the rectangle. Suppose the long pink oval represents all the wooden houses in the world. And, suppose the green circle represents Canada. The most logical conclusion one can draw from the figure is: A. B. C. D. all wooden houses are found in Canada Everyone lives in a wooden house Some Canadians live in wooden houses No one lives in Canada

DEDUCTIVE REASONING #7 � Suppose the following statements are all true: � � Person L is shorter than person X Person Y is shorter than person L Person M is shorter than person Y A. B. C. D. E. Person L is taller than J Person X is taller than J Person J is taller than L Person J is taller than M Person M is taller than Y What additional piece of information would be required to conclude that “Person Solution: Answer C Y is shorter than M<Y<L<X Person J”? So, if J is taller than L, Y must be shorter than J

DEDUCTIVE REASONING #8 A mother wants to order one large pizza, with exactly 5 toppings for her three picky children. She can choose from 7 toppings; cheese, mushrooms, olives, ham, sausage, onions, and pineapple. � � � Fifi says there has to be pineapple Mona says there cannot be any olives Rex says that if there is going to be sausage, then there has to be ham too. Which combination of toppings should she select if she is to satisfy all three children’s combined demands? A. B. C. D. pineapple, onions, cheese, mushrooms, sausage cheese, sausage, ham, olives, pineapple cheese, mushrooms, ham, onions, pineapple sausage, mushrooms, onions, cheese, and ham.

� http: //www. internet 4 classrooms. com/grade_l evel_help/logic_deductive_inductive_languag e_arts_seventh_7 th_grade. htm