REASONING LOGICAL ARGUMENT ARGUMENT An argument is a

REASONING LOGICAL ARGUMENT

ARGUMENT An argument is a pattern of reasonign that encourages the making of conclusion based on logical thinking An argument consists of 2 premises and a conclusion. There are 3 types of Arguments

Type 1 Argument (Deductive Reasoning) Premise 1: All A (things/objects) are B (situation) Premise 2: C (specific things) is A Conclusion: C is B

Example of Type 1 Argument Premise 1: All men are mortal. Premise 2: Einstein is a man. Conclusion: Einstein is mortal. Premise 1: All even numbers are divisible by 2 Premise 2: 30 is an even number Conclusion: 30 is divisible by 2. 30 ialah nombor genap

Activity Make your own examples of Type 1 Argument. One is non-mathematical example and another with a mathematical example.

Type 2 Argument (Direct Reasoning Argument) Premise 1: If P happens then Q happens (Implication) Premise 2: P happens (antecedent happens) Conclusion: Q happens (consequence happens)

Example of Type 2 Argument Premise 1: If a number is a factor of 12 then that number is a factor of 24 Premise 2: 3 is a factor of 12 Conclusion: 3 is a factor of 24

Example Premise 1: If a set has m elements the that set has 2 m subsets. Premise 2: Set P has 5 elements. Conclusion: Set P has 25 subsets.

Activity Create one mathematical example using Type 2 Arguments

Type 3 Arguments (Indirect Reasoning Argument) Premise 1: If p happens, then q happens Premise 2: q does not happen Conclusion: p does not happens

Example of Type 3 Argument Premise 1: If m is an interger then 2 m is an even number Premise 2: 2 m is not an even number Conclusion: m is not an integer

Premise 1: If n is an odd number then (n+1) is an even number Premise 2: (n + 1) in not an even number Conclusion: n is not an odd number

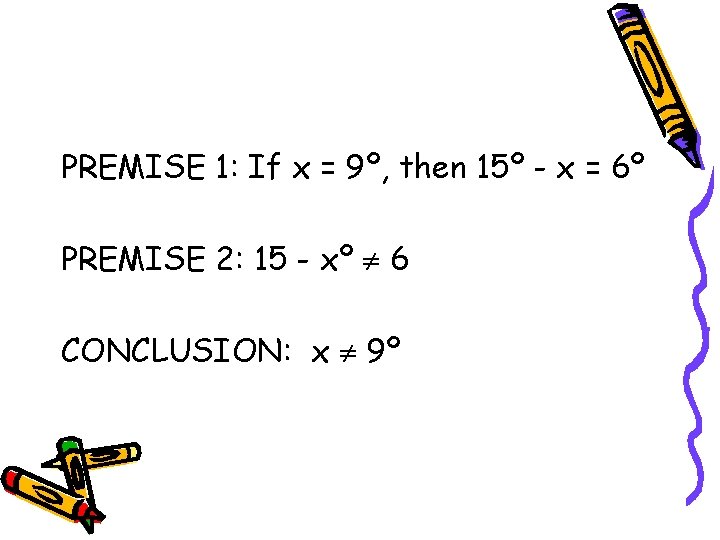
PREMISE 1: If x = 9º, then 15º - x = 6º PREMISE 2: 15 - xº 6 CONCLUSION: x 9º

ARUHAN Satu proses membuat kesimpulan umum berdasarkan kes-kes khusus Contoh bukan matematik: Carlos suka main guitar(kes khusus) Ceasar suka main guitar(kes khusus) Calvin suka main guitar(kes khusus) Catherine suka main guitar(kes khusus) Cheong suka main guitar(kes khusus) Kesimpulan umum: Semua orang yang namanya bermula dengan huruf C suka main guitar.

CONTOH MATEMATIK Diberi 5, 8, 11, 14, … boleh ditulis sebagai 5 = 5 + 3(0) 8 = 5 + 3(1) 11 = 5 + 3(2) 14 = 5 + 3(3) kesimpulan umum: Nombor berpola di atas boleh ditulis dalam bentuk 5 + 3 n, n = 0, 1, 2, 3…. .

CONTOH Buat kesimpulan secara aruhan bagi senarai no 8, 23, 44, 71, … yang mengikut pola berikut: 8 = 3(2)2 – 4 23 = 3(3)2 – 4 44 = 3(4)2 – 4 71 = 3(5)2 – 4 Kesimpulan: Nombor berpola di atas boleh ditulis dalam bentuk 3 n 2 – 4, n = 2, 3, 4, 5, ….

DEDUKSI Deduksi ialah satu proses membuat kesimpulan khusus berdasarkan pernyataan umum. CONTOH Pernyataan umum: am an = am+n Kesimpulan khusus: 33 35 = 38

CONTOH Suatu set yang mengandungi k unsur mempunyai 2 k subset. Cari bilangan subset bagi set P ={ 0, 1, 5, 6} Bilangan subset bagi set P = 24 = 16