Reasoning as Search Reasoning We can describe reasoning

Reasoning as Search

Reasoning We can describe reasoning as search in a space of possible situations.

State Space Search We need: • A set of states • A start state • A set of operators (a successor function), possibly with costs attached. • A set of goal states (or a way to test for goal)

Recall the 8 -Puzzle What are the states? http: //www. javaonthebrain. com/java/puzz 15/

A Water Jug Problem You are given two jugs, a 4 -gallon one and a 3 -gallon one. Neither has any measuring markers on it. There is a pump that can be used to fill the jugs with water. How can you get exactly 2 gallons of water into the 4 -gallon jug? States: Start state: Operators: Goal state:

School Lunch Planning States: Start state: Operators: Goal state:

Criminal Defense Lawyer States: Start state: Operators: Goal state:
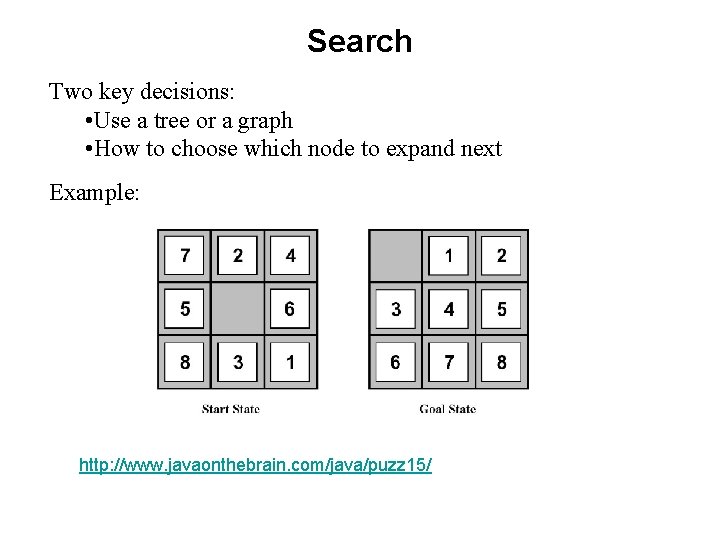
Search Two key decisions: • Use a tree or a graph • How to choose which node to expand next Example: http: //www. javaonthebrain. com/java/puzz 15/

Performance Criteria • Completeness • Optimality • How good is the solution? • How efficient is the search algorithm at finding the solution?
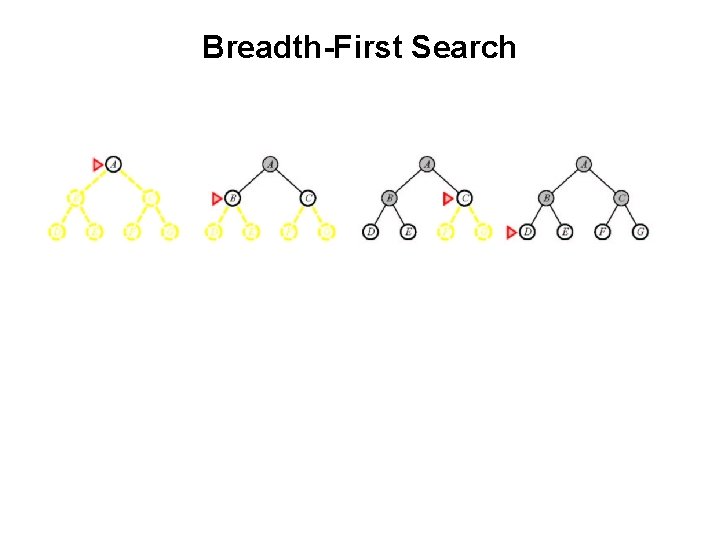
Breadth-First Search
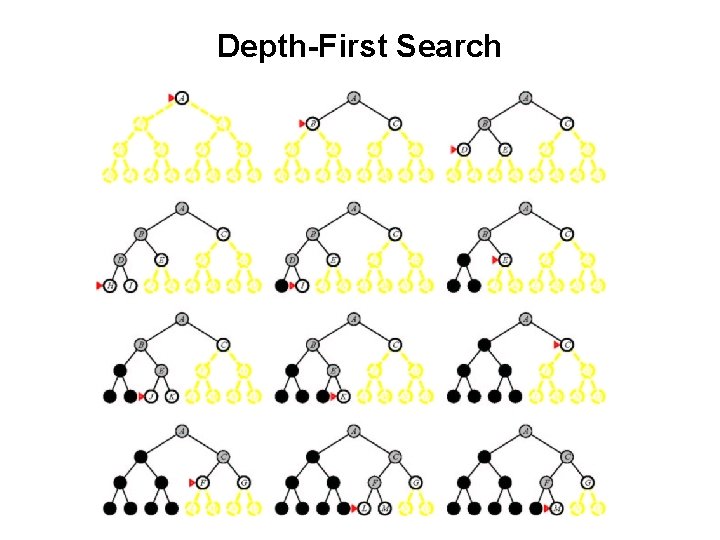
Depth-First Search

The British Museum Algorithm A simple algorithm: Generate and test When done systematically, it is basic depth-first search. But suppose that each time we end a path, we start over at the top and choose the next path randomly. If we try this long enough, we may eventually hit a solution. We’ll call this The British Museum Algorithm or The Monkeys and Typewriters Algorithm http: //www. arn. org/docs 2/news/monkeysandtypewriters 051103. htm
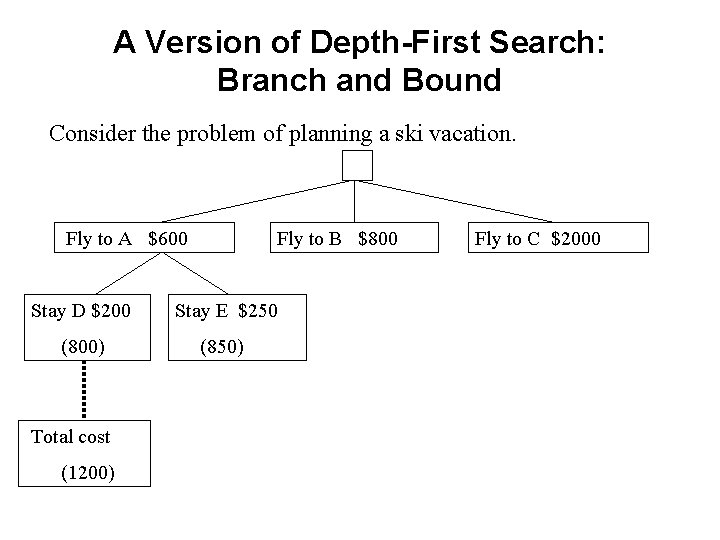
A Version of Depth-First Search: Branch and Bound Consider the problem of planning a ski vacation. Fly to A $600 Fly to B $800 Stay D $200 Stay E $250 (800) (850) Total cost (1200) Fly to C $2000

Problem Reduction Goal: Acquire TV Steal TV Earn Money Buy TV Or another one: Theorem proving in which we reason backwards from theorem we’re trying to prove.

Heuristics The word heuristic comes from the Greek word (heuriskein), meaning “to discover”, which is also the origin of eureka, derived from Archimedes’ reputed exclamation, heurika (“I have found”), uttered when he had discovered a method for determining the purity of gold. We typically use the term heuristic to refer to a technique that is likely, but not guaranteed, to produce a good (but not necessarily best) answer or the best answer with a good but not necessarily best expenditure of effort.

Heuristic Functions The job of a heuristic function f(n) is to evaluate a node n in a search tree so that the “best” node can be selected for expansion. Two approaches to defining f: • f measures the value of the state contained in the node. • f measures the cost of the state (and possibly the path to it). Often, in this case, we decompose f: f(n) = g(n) + h(n), where g(n) = the cost to get to n, and h(n) = an estimate of the cost to get from n to a goal

Examples - f Measures the Value Often, in these cases, f is the weighted sum of a set of component values: • Chess • School lunch planning • Autonomous Mars rover • Perry Mason defense lawyer

Examples – f Measures the Cost to a Goal In many problems, all goal states are equally good. Then all we care about is the cost of getting to one. So a state is good if the estimated cost of getting from it to a goal is low. Or we may also want to take into account the cost, so far, of getting to it. • 8–Puzzle • Water jug • Route planning

Hill Climbing Problem: You have just arrived in Washington, D. C. You’re in your car, trying to get downtown to the Washington Monument.
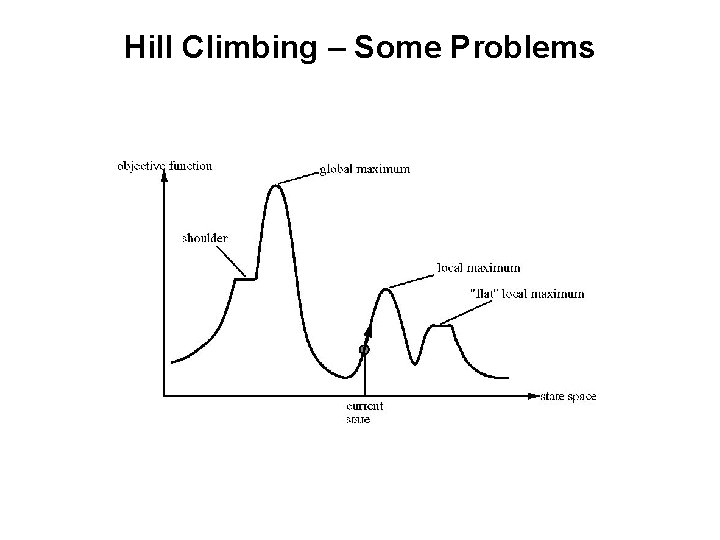
Hill Climbing – Some Problems

Sometimes the Problem is f From the initial state, move A to the table. Three choices for what to do next. A local heuristic function: Add one point for every block that is resting on the thing it is supposed to be resting on. Subtract one point for every block that is sitting on the wrong thing.
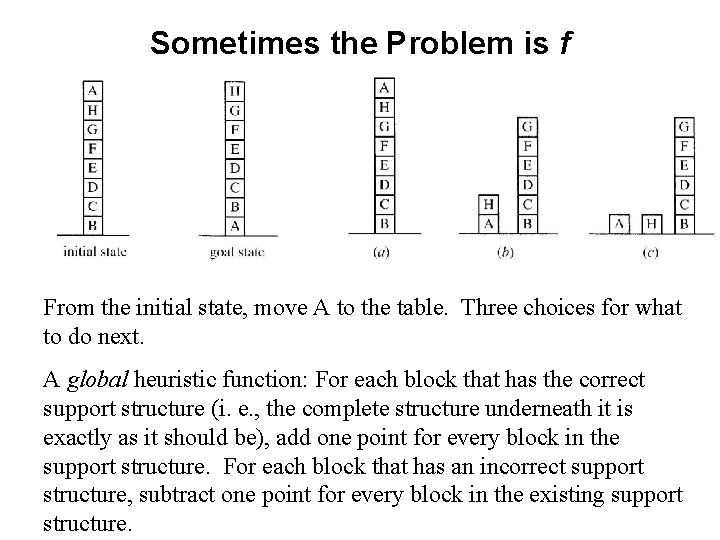
Sometimes the Problem is f From the initial state, move A to the table. Three choices for what to do next. A global heuristic function: For each block that has the correct support structure (i. e. , the complete structure underneath it is exactly as it should be), add one point for every block in the support structure. For each block that has an incorrect support structure, subtract one point for every block in the existing support structure.
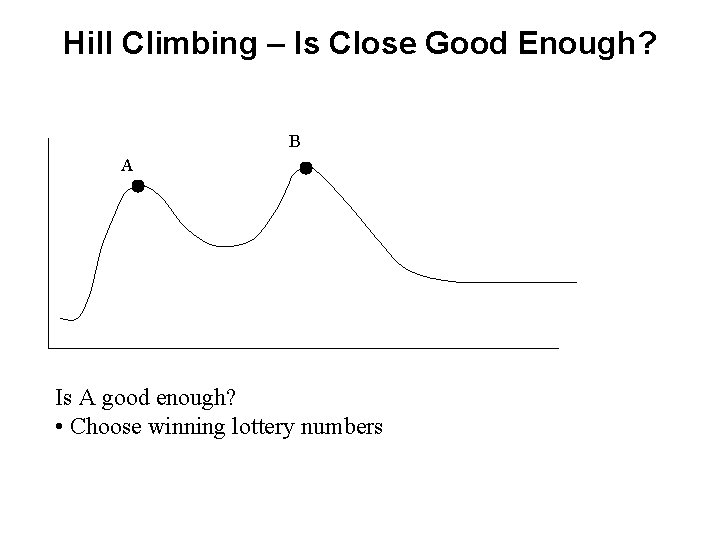
Hill Climbing – Is Close Good Enough? B A Is A good enough? • Choose winning lottery numbers
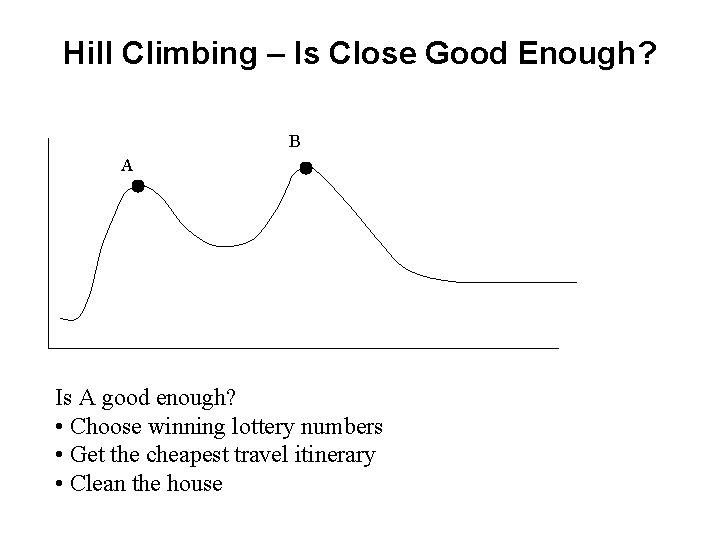
Hill Climbing – Is Close Good Enough? B A Is A good enough? • Choose winning lottery numbers • Get the cheapest travel itinerary • Clean the house
- Slides: 24













































