GEOMETRY Chapter 9 9 1 Similar Right Triangles

GEOMETRY: Chapter 9 9. 1 Similar Right Triangles

Theorem 9. 1 If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other. Image taken from: Geometry. Mc. Dougal Littell: Boston, 2007. P. 449.

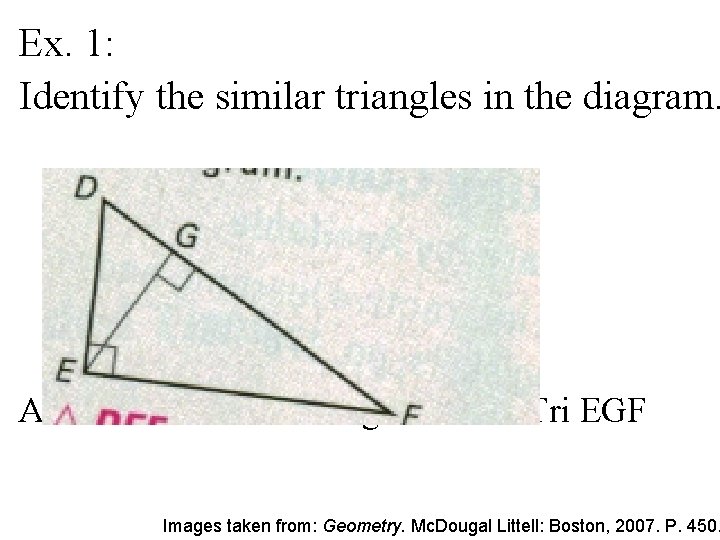
Ex. 1: Identify the similar triangles in the diagram. Answer: tri DEF ~ triangle DGE ~ Tri EGF Images taken from: Geometry. Mc. Dougal Littell: Boston, 2007. P. 450.

Ex. 2: The figure below shows the side view of a tool shed. What is the maximum height, h, of the shed? Answer: 16. 1 ft Images taken from: Geometry. Mc. Dougal Littell: Boston, 2007. P. 450.

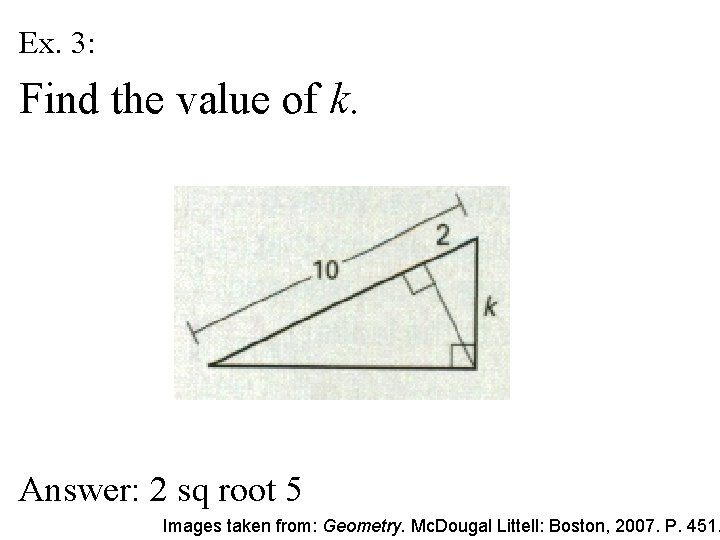
Ex. 3: Find the value of k. Answer: 2 sq root 5 Images taken from: Geometry. Mc. Dougal Littell: Boston, 2007. P. 451.

Theorem 9. 2 Geometric Mean (Altitude) Theorem In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. The length of the altitude is the geometric mean of the lengths of the other two sides. Images taken from: Geometry. Mc. Dougal Littell: Boston, 2007. P. 452.

Theorem 9. 3 Geometric Mean (Leg) Theorem In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. The length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse that is adjacent to the leg. Images taken from: Geometry. Mc. Dougal Littell: Boston, 2007. P. 452.

Ex. 4: You are standing by a tree as shown in the diagram. A 25 foot ladder is leaning against the tree. What is the length of a piece of rope that goes from the base of the tree and is perpendicular to the ladder? Answer: 4. 9 ft Images taken from: Geometry. Mc. Dougal Littell: Boston, 2007. P. 452.

9. 1, p. 531, #1 -29 odds (15 questions)