Geometry Chapter 2 Reasoning and Proof What you

Geometry Chapter 2: Reasoning and Proof

What you will learn today: n Make conjectures based on inductive reasoning n Find counterexamples n Create conjunctions and disjunctions n Determine truth values of conjunctions and disjunctions

2. 1: Inductive Reasoning and Conjecture n A conjecture is an educated guess based on known information. n Example: n Inductive reasoning is reasoning that uses a number of specific examples to arrive at a generalization or prediction.

Example One: n For points P, Q, and R, PQ = 9, QR = 15, and PR = 12. Make a conjecture and draw a figure to illustrate your conjecture.

You Do It: n For points L, M, and N, LM = 20, MN = 6, and LN = 14. Make a conjecture and draw a figure to illustrate your conjecture.

Counterexample n Conjectures are based on several observations that are mostly true. n It only takes one false example to prove a conjecture is not true. n The false example is called a counterexample.

Example Two: n Determine whether each conjecture is true or false. Give a counter example for any false conjecture. n Given: m + y ≥ 10, y ≥ 4 Conclusion: m ≤ 6 n Given: noncollinear points R, S, and T Conclusion:

You Do It n Determine whether each conjecture is true or false. Give a counterexample for any specific false conjecture. n Given: WXYZ is a rectangle Conclusion WX = YZ and WZ = XY n Given: JK = KL = LM = JM Conclusion: JKLM is a square

2. 2: Logic n A statement is any sentence that is either true or false, but not both. n Example: p: Today is Friday n Where a statement is true or false is its truth value. n Example: p is true

Logic n The negation of a statement has the opposite meaning as well as an opposite truth value. n Example: ~p: Today is not Friday n Truth value of ~p is false n Two or more statements can be joined to form a compound statements.

Compound Statements n A conjunction is a compound statement formed by joining two or more statements with the word and. Symbols: p and q p ˄ q n Both statements have to be true for the conjunction to be true. n Example: n n n p: Raleigh is a city in NC. q: Raleigh is the capital of NC. § p ˄ q: Raleigh is a city in NC and Raleigh is the capital of NC.

Example One n Use the following statements to write a compound statement for each conjunction. Then find its truth value. n n n p: January 1 is the first day of the year q: -5 + 11 = -6 r: A triangle has three sides n p ˄ q n ~r ˄ q n ~q and r

You Do It n Use the following statements to write a compound statement for each conjunction. Then find its truth value. p: One foot is 14 inches n q: September has 30 days n r: A plane is defined by three noncollinear points n n p˄q n r ˄ ~p n ~q ˄ r

Disjunction n A disjunction is a compound statement formed by joining two or more statements with word or. Symbols: p or q p v q n Only one statement has to be true for the disjunction to be true n Example: n n n p: Raleigh is a city in NC q: Raleigh is the capital of NC § p v q: Raleigh is a city in NC or Raleigh is the capital of NC

Example Two n Use the following statements to write a compound statement for each disjunction. Then find its truth value. p: 100 ÷ 5 = 20 n q: The length of a radius of a circle is twice the length of its diameter n n p or q n ~p v ~q

You Do It n Use the following statements to write a compound statement for each disjunction. Then find its truth value. p: is proper notation for “line AB” n q: centimeters are metric units n r: 9 is a prime number n n pvq n ~q v r

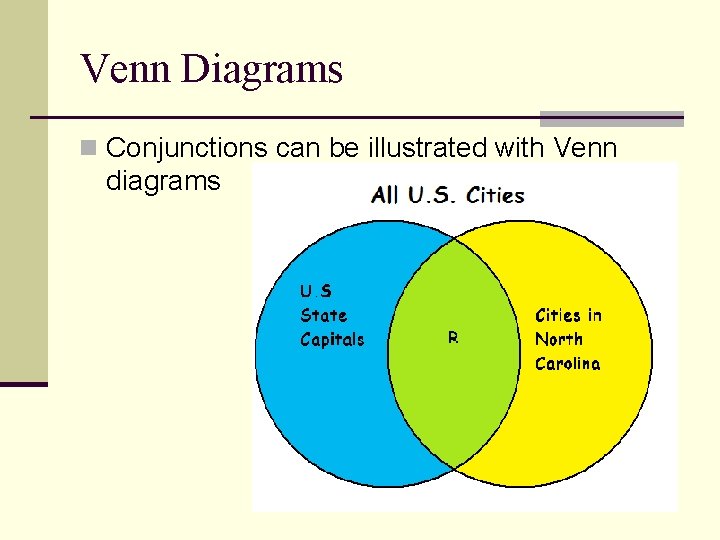
Venn Diagrams n Conjunctions can be illustrated with Venn diagrams

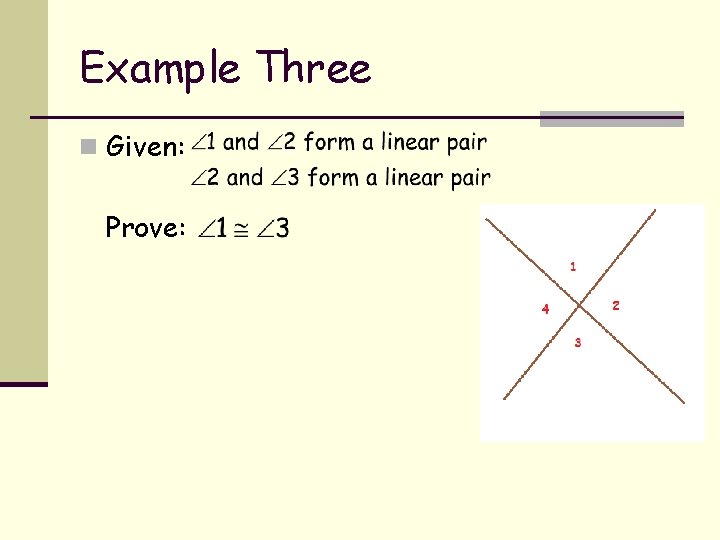
Example Three

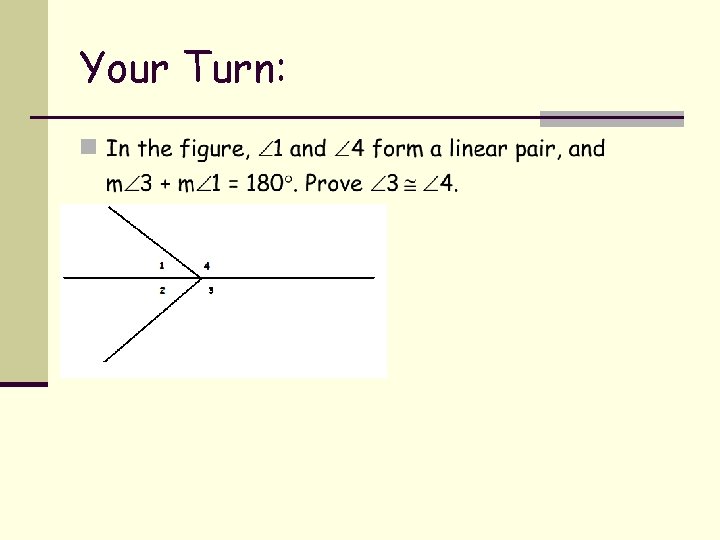
You Do It

Classwork n Complete the following assignment and turn it in when you are finished (this way you don’t have homework over the weekend ) n Worksheet Both sides – all problems n Will be graded for accuracy n

Warm - Up n Make a conjecture about the following: n n Determine whether the following is true or false. Give a counterexample if the statement is false n n n A, B, and C are points. AB = 2, BC = 4, and AC = 3 Given: Points A, B, and C are collinear. Conclusion: AB + BC = AC Given: Conclusion: Create the compound statement and determine the truth value. n n p: 10 + 8 = 18 q: A rectangle has 3 sides n p ˄ ~q n ~p v ~q

2. 3: Conditional Statements n Analyze statements in the if – then form. n Write the converse, inverse, and contrapositive of if – then statements. n Write and understand biconditional statements. n n Get $1500 cash back when you buy a new car. Free cell phone with every one – year service enrollment.

n The statements on the previous slide are examples of conditional statements. n A conditional statement is a statement that can be written in the if-then form. n Example: n n Get $1500 cash back when you buy a new car. If you buy a car, then you get $1500 cash back.

If – then statement n An if – then statement is written in the for if p, then q. n The phrase immediately following the word if is called the hypothesis The phrase immediately following the word then is called the conclusion n p → q, read if p then q, or p implies q. n

Example 1 n Identify the hypothesis and conclusion for each statement. n n If points A, B, and C lie on line m, then they are collinear. The Tigers will play in the tournament if they win their next game.

Your Turn n Identify the hypothesis and conclusion of each statement. n n If a polygon has 6 sides, then it is a hexagon. Tamika will advance to the next level of play if she completes the maze in her computer game.

Writing statements in if – then form n Some statements are conditional but are not in if – then form. n It is easier to identify the hypothesis and conclusion before writing the sentence in if – then form n Example: n All apes love bananas n Hypothesis: An animal is an ape n Conclusion: It loves bananas n If – then: If an animal is an ape, then it loves bananas

Example 2 n Identify the hypothesis and conclusion of each statement. Then write each statement in the if – then form. n n An angle with a measure greater than 90 is an obtuse angle. Perpendicular lines intersect.

Your Turn n Identify the hypothesis and conclusion of each statement. Then write each statement in the if – then form. n Distance is positive. n A five – sided polygon is a pentagon.

Truth Value n All cases of conditional statements are true except where the hypothesis is true and the conclusion is false. p q p→q T T F F F T T F F T

Example 3 n Determine the truth value of the following statement for each set of conditions If you get 100% on your test, then your teacher will give you an A. n You get 100%; your teacher gives you an A n n You get 100%; your teacher gives you a B n n False You get 98%: your teacher gives you an A n n True You get 85%; your teacher gives you a B n True

Your Turn n Determine the truth value of the following statement for each set of conditions If Parker rests for 10 days, his ankle will heal. n n Parker rests for 10 days, and he still has a hurt ankle n False n True Parker rests for 3 days, and he still has a hurt ankle Parker rests for 10 days, and he does not have a hurt ankle anymore Parker rests for 7 days, and he does not have a hurt ankle anymore

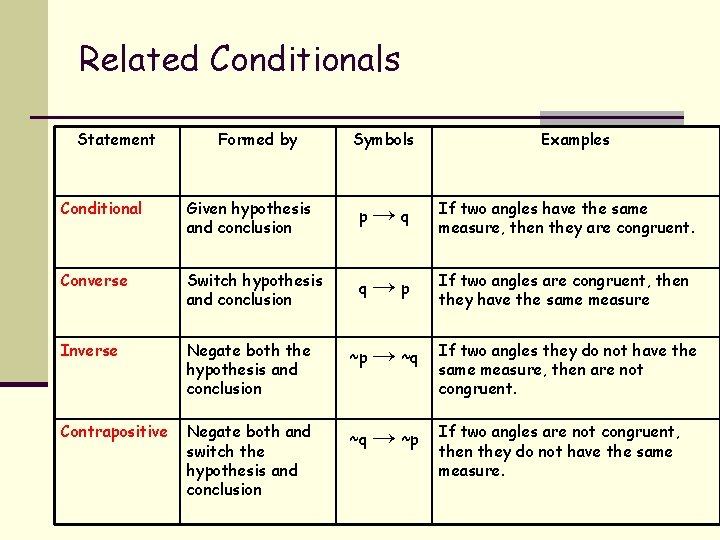
Related Conditionals Statement Formed by Symbols Examples Conditional Given hypothesis and conclusion p→q If two angles have the same measure, then they are congruent. Converse Switch hypothesis and conclusion q→p If two angles are congruent, then they have the same measure Inverse Negate both the hypothesis and conclusion ~p Contrapositive Negate both and switch the hypothesis and conclusion ~q → ~p → ~q If two angles they do not have the same measure, then are not congruent. If two angles are not congruent, then they do not have the same measure.

n You can not determine any relationship between a conditional and the converse and inverse as far as truth value. n However, the following is true: n The truth value of the conditional and contrapositive will always be the same n The truth value of the converse and the inverse will always be the same n Statements with the same truth values are said to be logically equivalent n Conditional and Contrapositive are logically equivalent n Converse and Inverse are logically equivalent

Example 3 n Write the conditional, converse, inverse, and contrapositive of the statement: Linear pairs of angles are supplementary. Determine whether each statement is true or false. If a statement is false, give a counterexample.

Your Turn n Write the conditional, converse, inverse, and contrapositive of the statement: All squares are rectangles. Determine whether each statement is true or false. If the statement is false, give a counterexample.

Biconditional Statement n A biconditional statement is the conjunction of a conditional statement and its converse. (p → q) ^ (q → p) is written p ↔ q, and read p if and only if q, can be abbreviated iff n Both the conditional and the converse must be true for a biconditional to be true. n

Example 4 n Write each biconditional as a conditional and its converse. Then determine whether the biconditional is true or false. If false, give a counterexample. n Two angles measures are complements if and only if their sum is 90. n x > 9 iff x > 0

Your Turn n Write each biconditional as a conditional and its converse. Then determine whether the biconditional is true or false. If false, give a counterexample. n A calculator will run if and only if it has batteries. n 3 x – 4 = 30 iff x = 7

Homework n Workbook n Section 2. 3 n n 1 – 10 (all) You do not have any practice on the biconditional statement. Make sure you know how to create statements and know the truth value. It will be covered on your quiz tomorrow!

Warm - Up n Identify the hypothesis and conclusion of each statement n If 2 x + 6 = 10, then x = 2 n Write each statement in if – then form n n Get a free visit with a one – year fitness plan Vertical angles are congruent n Write the converse, inverse, and contrapositive of each conditional statement. Determine whether each related conditional is true or false. n All rectangles are quadrilaterals n If you live in Dallas, then you live in Texas.

Homework H: 3 x + 4 = -5; C : x = -3 H: you take a class in television broadcasting; C = you will film a sporting event 3. If you do not remember the past, then you are condemned to repeat it. 4. If two angles are adjacent, then they share a common vertex and a common side. 5. True 6. True 7. True 8. Converse: If -8 > 0 then (-8)2 > 0; true Inverse: If (-8)2 ≤ 0, then -8 ≤ 0 true Contrapositive: If – 8 ≤ 0, then (-8)2 ≤ 0; false 9. If you are a junior, then you wait on tables 10. If you wait on tables, then you are a junior 1. 2.

Quiz Time n Please clear off your desk n You will have plenty of time to complete your quiz n When you are finished, please remain quiet until everyone else has finished. n We will begin 2. 4: Deductive Reasoning with the Law of Detachment and Law of Syllogism

2. 4: Deductive Reasoning n Use the Law of Detachment n Use the Law of Syllogism n When you are ill, your doctor may prescribe an antibiotic to help you get better. Doctors may use a dose chart to determine the correct amount of medicine based on your weight.

n The process that the doctors use to determine the amount of medicine a patient should take is called deductive reasoning. n Deductive reasoning uses facts, rules, definitions, or properties to reach a logical conclusion. n One way to do this is the Law of Detachment.

Law of Detachment n If p → q is true and p is true, then q is also true. n Example:

Example 1 n The following is a true conditional. Determine whether each conclusion is a valid based on the given information. Explain your reasoning. If a ray is an angle bisector, then it divides the angle into two congruent angles. n n

Your Turn n The following is a true conditional. determine whether each conclusion is a valid based on the given information. Explain your reasoning. If two segments are congruent and the second segment is congruent to a third segment, then the first segment is also congruent to the third. n Given: WX = UV and UV = RT. Conclusion: WX = RT. n Given: UV and WX = RT. Conclusion: WX = UV and UV = RT

Law of Syllogism n If p →q and q → r are true, then p → r is also true. n Another way to look at the transitive property. n Some statements may not be written in conditional form. It may be easier to see the Law of Syllogism when statements are written in conditional form n Example:

Example 2 n Use the Law of Syllogism to determine whether a valid conclusion can be reached from each set of statements. n n (1) If the symbol of a substance is Pb, then it is lead. (2) The atomic number of lead is 82. (1) Water can be represented by H 2 O. (2) Hydrogen (H) and Oxygen (O) are in the atmosphere.

Your Turn n Use the Law of Syllogism to determine whether a valid conclusion can be reached from each set of statements. n n (1) If Ashley attend the prom, she will go with Mark. (2) Mark is a 17 – year old student. (1) If Mel and his date eat at the Peddler Steakhouse before going to the prom, they will miss the senior march. (2) The Peddler Steakhouse stays open until 10 p. m.

Example 3 n Determine whether the statement (3) follows from statements (1) and (2) by the Law of Detachment of the Law of Syllogism. If it does, state which law was used. If it does not, write invalid. (1) Vertical angles are congruent. (2) If two angles are congruent, then their measures are equal. (3) If two angles are vertical, then their measures are equal.

(1) If a figure is a square, then it is a polygon. (2) Figure A is a polygon. (3) Figure A is a square.

Your Turn (1) If the sum of the squares of two sides of a triangle is equal to the square of the third side, then the triangle is a right triangle. (2) For ∆XYZ, XY 2 + YZ 2 = XZ 2 (3) ∆XYZ is a right triangle

Your Turn (cont. ) (1) If Ling wants to participate in the wrestling competition, he will have to meet an extra three times a week to practice. (2) If Ling adds anything extra to his weekly schedule, he cannot take karate lessons. (3) If Ling wants to participate in the wrestling competition, he cannot take karate lessons.

Classwork n Worksheet n Section 2. 4 n 1– 7

Homework n Workbook n Section 2. 4 n 1 – 7 (all)

Warm - Up n Use the Law of Syllogism to determine whether a valid conclusion can be reached from the set of statements. n If it rains, then the field will be muddy. If the field is muddy, then the game will be cancelled n Determine whether the Law of Detachment or the Law of Syllogism was used to find the conclusion. n If it snows outside, you will wear your winter coat. It is snowing outside You wear your winter coat.

Homework 1. Valid 2. Invalid 3. If two angles form a linear pair, then the 4. 5. 6. 7. sum of their measures is 180 If a hurricane is Category 5, then trees, shrubs, and signs are blown down. Yes; Law of Detachment Invalid If a virus is a parasite, then it harms its host.

2. 5: Postulates and Paragraph Proofs n Identify and use basic postulates about points, lines, and planes. n Write paragraph proofs.

n Postulate – a statement that describes a fundamental relationship between the basic terms of geometry. n Postulates are accepted as true. n The ideas of points, lines, and planes from Chapter 1 are considered postulates.

Postulates n 2. 1: Through any two points, there is exactly one line n 2. 2: Through any three points not on the same line, there is exactly one plane.

Example One: n Jesse is setting up a network for his mother’s business. There are five computers in her office. He wants to connect each computer to every other computer so that if one computer fails, the others are still connected. How many connections does Jesse need to make?

Your Turn: n Some snow crystals are shaped like regular hexagons. How many lines must be drawn to interconnect all vertices of a hexagonal snow crystal? n Donna is setting up a network for her company. There are 7 computers in her office. She wants to connect each computer to every other computer so that if one computer fails, the others are still connected. How many connections does Donna have to make?

More Postulates n 2. 3: A line contains at least two points. n 2. 4: A plane contains at least three points not on the same line.

More Postulates n 2. 5: If two points lie in a plane, then the entire line containing those points lies in that plane. n 2. 6: If two lines intersect, then their intersection is exactly one point. n 2. 7: If two planes intersect, then their intersection is a line.

Example Two n Determine whether each statement is always, sometimes, or never true. Explain. n If points A, B, and C lie in plane M, then they are collinear. n Sometimes. n There is exactly one plane that contains noncollinear points P, Q, and R. n Always. n There at least two lines through points M and N. n Never.

Your Turn: n Determine whether each statement is always, sometimes, or never true. Explain. n The intersection of plane M and plane N is a point n Never. n If A and B lie in plane W, then line AB lies in plane n Always. n Segment TR lines in plane M. n Sometimes.

Paragraph Proofs n Undefined terms, definitions, postulates, and algebraic properties of equality are used to prove that other statements or conjectures are true. n Example of this is a theorem – statement that has been shown to be true.

Paragraph Proofs n Proof – a logical argument in which each statement is supported by a statement that is accepted as true. n Paragraph Proof (Informal Proof) – you write a paragraph to explain why a conjecture for a given statement is true.

Five essential parts of a good proof: n State theorem or conjecture to be proven n List the given information n If possible, draw a diagram to illustrate the given information n State what is to be proved n Develop a system of deductive reasoning

Example Three n Given that M is the midpoint of segment PQ, write a paragraph proof to show that PM is congruent to MQ.

Your Turn: n Given line AC intersecting line CD, write a paragraph proof to show that A, C, and D determine a plane.

One More Example: n Given that is the angle bisector of CAD, write a paragraph proof to show that CAB DAB.

Midpoint Theorem n Theorem 2. 8: If M is the midpoint of segment AB, then AM is congruent to MB.

2. 6: Algebraic Proof n Use algebra to write two – column proofs n Use properties of equality in geometry. n Lawyers develop their cases using logical arguments based on evidence to lead a jury to a conclusion favorable to their case.

Algebraic Proof n You have learned to use properties of equality to solve equations and verify relationships. n Algebra is a system of mathematics with sets of numbers, operations, and properties that allow you to perform algebraic operations.

In your textbook on page 94 Reflexive Property a=a Symmetric Property If a = b, then b = a Transitive Property If a = b and b = c, then a = c Add/Subtract Property If a = b, then a + c = b + c and a – c = b – c Multiply/Divide Property If a = b, then a ∙c = b ∙ c and a ÷ c = b ÷ c Substitution Property If a = b, then a can replace b anywhere Distributive Property a(b + c) = ab + ac

Example 1 n Solve 3(x – 2) = 42.

Your Turn n Solve 2(5 – 3 a) – 4(a + 7) = 92

n Two – column proof (formal proof) contains statements and reasons organized in two columns. n Each step is called a statement and the properties that justify each step are called reasons.

Example 2 n Write a two – column proof. n

Your Turn n Write a two – column proof. n n

Geometric Proof n Geometry uses variables, numbers, and operations. n Segment measures and angle measures are real numbers, so properties from algebra can be used to discuss their relationships.

Example 3 n On a clock, the angle formed by the hands at 2: 00 is a 60º angle. If the angle formed at 2: 00 is congruent to the angle formed at 10: 00, prove that the angle at 10: 00 is a 60º angle.

Your Turn n A starfish have five arms. If the length of arm 1 is 22 cm, and arm 1 is congruent to arm 2, and arm 2 is congruent to arm 3, prove that arm 3 has length of 22 cm.

Homework n Workbook n Page 11 n n 1 -6 Page 12 n 1 and 2

Warm - Up n Determine whether the following are sometimes, always, or never true Three points determine a plane n Points G and H are in plane X. Any point collinear with G and H is in plane X. n The intersection of two planes can be a point. n n Create a two – column proof to prove the following: n Given: 2 x – 7 = ½x – 1 Prove: x = 4

Homework

Homework (cont. )

2. 7: Proving Segment Relationships n Write proofs involving segment addition n Write proofs involving segment congruence.

Ruler Postulate n The points on any line segment can be paired with real numbers so that, given any two points A and B on a line, A corresponds to zero, and B corresponds a positive real number. n Meaning, you can measure a segment with a ruler.

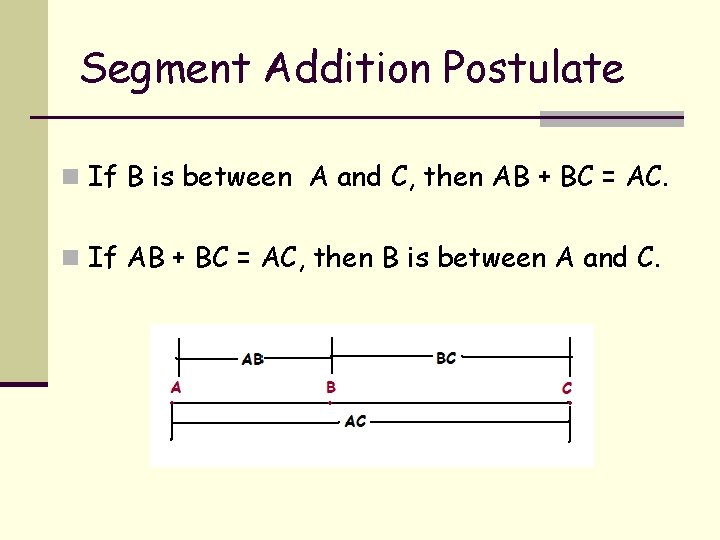
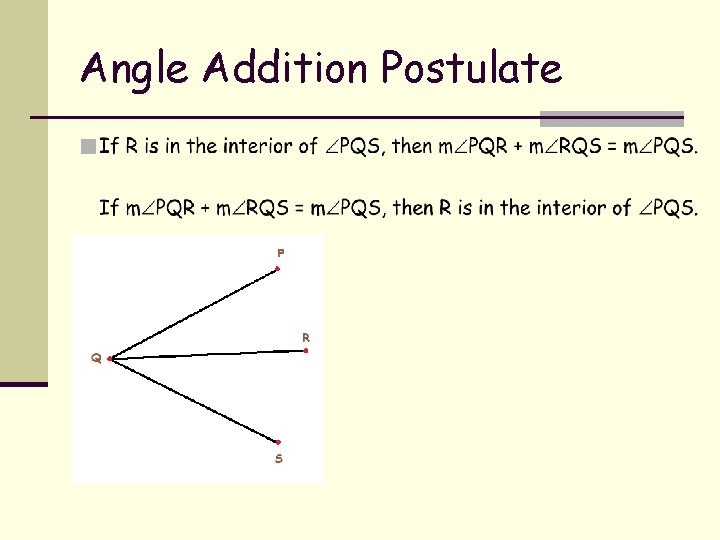
Segment Addition Postulate n If B is between A and C, then AB + BC = AC. n If AB + BC = AC, then B is between A and C.

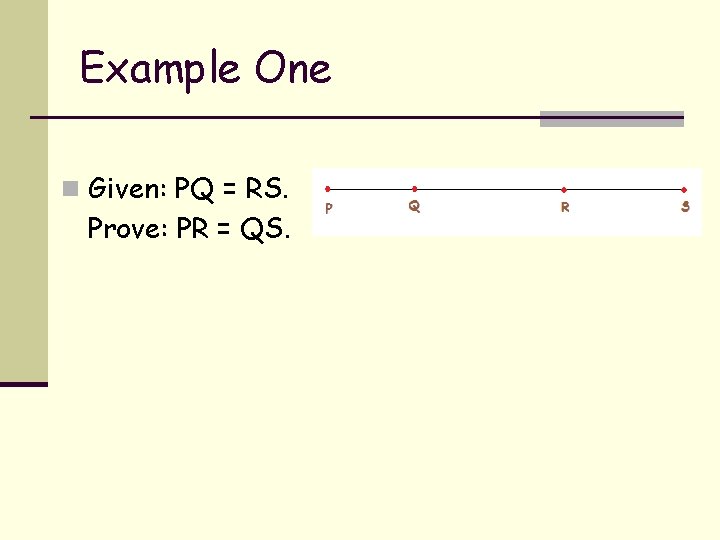
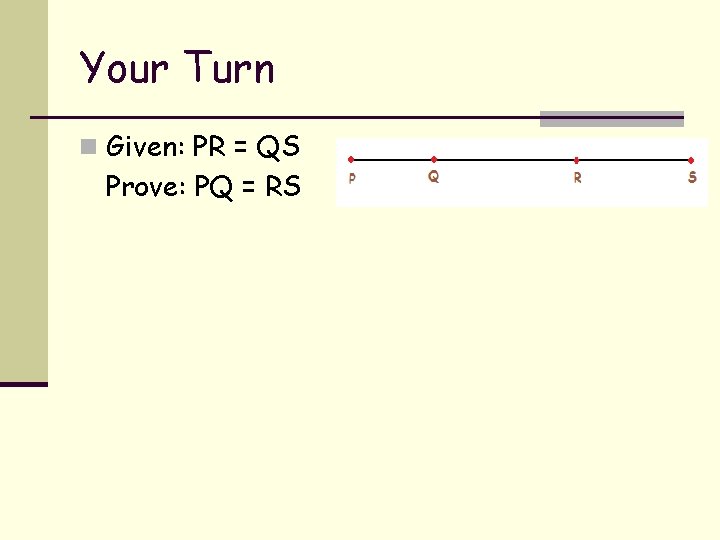
Example One n Given: PQ = RS. Prove: PR = QS.

Your Turn n Given: PR = QS Prove: PQ = RS

Segment Congruence n Reflexive: n Symmetric: n Transitive:

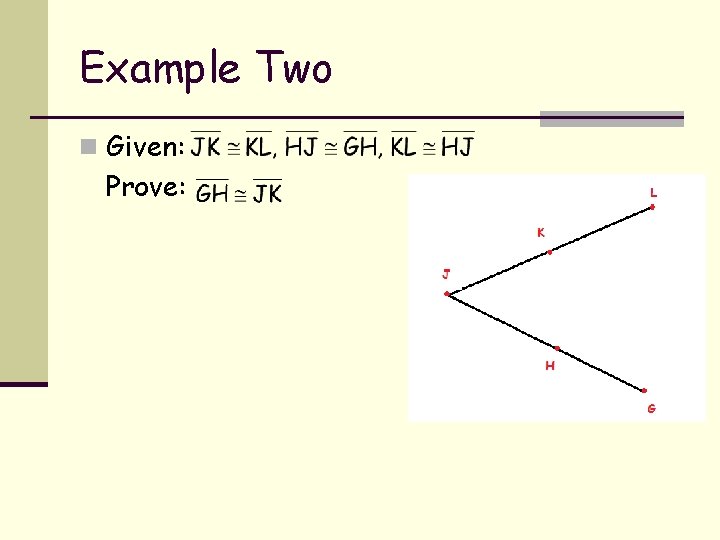
Example Two n Given: Prove:

Your Turn: n Given: Prove:

2. 8: Proving Angle Relationships n Write proofs involving supplementary and complementary angles. n Write proofs involving congruent and right angles.

Protractor Postulate n Given and a number r between 0 and 180, there is exactly one ray with endpoint A, extending on either side of , such that the measure of the angle formed is r. n Meaning you can use a protractor to measure an angle.

Angle Addition Postulate n

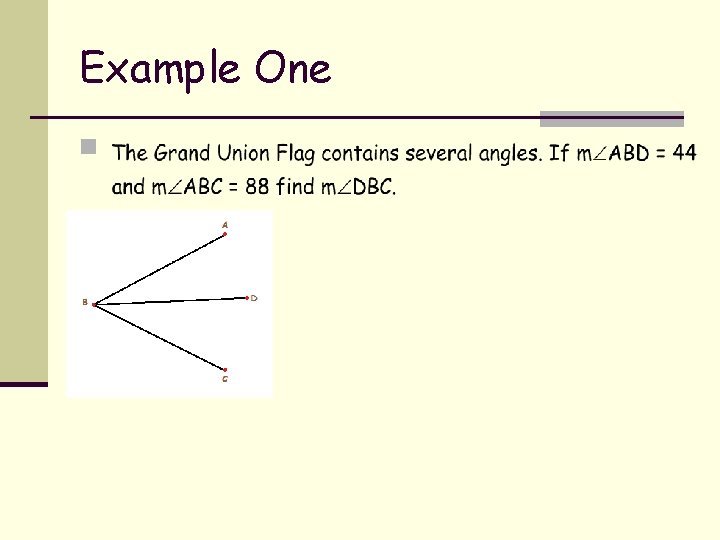
Example One n

Your Turn: n At 4 o’clock, the angle between the hour and minute hands of a clock is 120º. If the second hand stops where it bisects the angle between the hour and minute hands, what are the measures of the angles between the minute and second hands and between the second and hour hands?

Theorems n Supplement Theorem: If two angles form a linear pair, then they are supplementary angles. n Complement Theorem: If the noncommon sides of two adjacent angles form a right angle, then the angles are complementary angles.

Example Two: n If angle 1 and angle 2 form a linear pair and angle 2 = 67, find the measurement of angle 1.

Your Turn: n If angle 1 and angle 2 for a linear pair and angle 2 = 166, find the measurement of angle 1.

Congruency of Angles n Congruence of angles is reflexive, symmetric, and transitive.

Theorems n Angles supplementary to the same angle or to congruent angles are congruent. n Angles complementary to the same angle or to congruent angles are congruent.

Example Three n Given: Prove:

Your Turn: n

Vertical Angle Theorem n If two angles are vertical angles, then they are congruent.

Example Four: n

Your Turn: n

Right Angle Theorems n Perpendicular lines intersect to form four right angles. n All right angles are congruent. n Perpendicular lines form congruent adjacent angles.

Right Angle Theorems n If two angles are congruent and supplementary, then each angle is a right angle. n It two congruent angles form a linear pair, then they are right angles.

Classwork/Homework n Worksheet n Lesson 2. 7 n n Lesson 2. 8 n