Exploiting Vanishing Polynomials for Equivalence Verification of FixedSize

Exploiting Vanishing Polynomials for Equivalence Verification of Fixed-Size Arithmetic Datapaths GIEE , NTU ALCom Lab Presenter: 陳炳元

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

Bit-Vector Arithmetic = %2 m Algebra ØRepresent integers as a vector of bits ØBit x 0 represents values 0 or 1 ØVector X[1: 0] = {x 1, x 0} represents integers Ø 00, 01, 10, 11 ØBit-vector of size m: integer values in 0, …, 2 m-1 ØVector X[m-1 : 0] represents integers reduced % 2 m

Fixed-Size (m) Data-path: Modeling • Control the datapath size: Fixed size bit-vectors (m) • Bit-vector of size m: integer values in 0, …, 2 m-1 Fixed-size (m) bit-vector arithmetic Polynomials reduced %2 m Algebra over the ring Z 2 m

Anti-Aliasing Function ØF 1[15: 0] = 156 x 6 + 62724 x 5 + 17968 x 4 + 18661 x 3 + 43593 x 2 + 40244 x +13281 ØF 2[15: 0] = 156 x 6 + 5380 x 5 + 1584 x 4 + 10469 x 3 + 27209 x 2 + 7456 x + 13281 Now that polynomially F 1 F 2 because they have different coefficients; But because the datapath size is fixed to 16 bits F 1[15: 0]= F 2[15: 0], or in other words F 1 % 216 = F 2 % 216

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

Binary Relation • Let A be a set, R is a subset of A A, we say that R is a binary relation on A • Let R be a binary relation. We sometimes write a. Rb for (a, b) R • A binary relation R on A is called reflexive if(x, x) R for all x A • A binary relation R on A is called symmetric if(x, y) R (y, x) R for all x, y A • A binary relation R on A is called transitive if(x, y) R and (y, z) R (x, z) R for all x, y, z A

Equivalence Relation • A binary relation R on A is called equivalence relation if it is reflexive, symmetric, transitive • • A equivalence relation R on A. We define the equivalence class of a, [a]={b A| (a, b) R } • Example: Let A=Z , if (a, b) R a b mod n. Then [0], [1], …, [n-1] are all equivalence class

Partition • Let A be a set. A partition of A is a collection of disjoint nonempty subsets of A. The equivalence classes of R on A form a partition of A. Lemma 1: Let R be an equivalence relation on A. The following statements are equivalence: (1) (a, b) R (2) [a]=[b] (3) [a] [b] {}

Partition • Theorem 1: Let R be an equivalence relation on A. P={[a]| a A} P is partition of A pf: 顯然 Claim: [a] [b], then [a] [b]={} If [a] [b] {} By the lemma 1, we have [a]=[b] 故P為A之一partition

Partition • Example: • Let A=Z , if (a, b) R a b mod n. Then corresponding to equivalence class set Zn={[0], [1], …, [n-1]} Note: We sometimes write Zn={0, 1, …, n-1}

Binary Operation • Let S be a set. : S S S function, then we say that is a binary operation on S • if is a binary operation on S then we will write a b rather than (a, b). • (S, 1, 2, …, K) is a set S together with k binary operation 1, 2, …, K on S

Introduction to Rings • A ring (R, +, ‧) is a set, R together with two binary operation +, ‧on R called addition and multiplication, satisfying the following properties: (1)(R, +) is an abelin group. We write the identity element 0 (2)Multiplication is associative, means that a (b c)=(a b) c a, b, c R (3)The left and right distributive laws hold, means that a (b+c)=a b+a c and (a+b) c=a c+b c a, b, c R

Introduction to Rings • Example: 我們在Z上定義一個equivalence relation, 若(a, b) R a b mod n 對應之equivalence class set Zn={[0], [1], …, [n-1]}. 在Zn上定義兩個binary operation +, by [a]+[b]=[a+b mod n]與[a] [b]=[ab mod n] (Zn+, ‧): ring NOTE: (1) [a], [b] Zn, [a]+[b]=[a+b mod n]=[b+a mod n]=[b]+[a] and [a] [b]=[ab mod n]=[ba mod n]=[b] [a] (2) [a] Zn, [a]+[0]=]=[a+0 mod n]=[a] and [a] [1]=[a 1 mod n]=[a]

Introduction to Rings • A ring R is called a commutative ring if ab=ba a, b R • A ring R is called a ring with unity 1 if there is an element 1 0 in R such that 1 a=a=a 1 a R Example: (1) Z, Q, R, C: commutative ring with unity 1 where the ring operations are the usual addition and multiplication. (2)Let n be a positive integer. Then the set Zn={0, 1, …, n-1}, under addition and multiplication modulo n is commutative ring with unity 1.

Introduction to Rings • Let (R, +, ‧) be a ring, define by R[X]={anxn+an-1 xn-1+· · ·+a 1 x+a 0| n , ai R, i=1, 2, . . . , n} is called the ring of polynomials over R In fact, R[X] is ring Example: (Z 3, +, ‧), f(x)=2 x 3+1, g(x)=x+2 f(x)+g(x)= 2 x 3+x and f(x) g(x)=2 x 4+x 3+x+2=2 x 4+2 x+2

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

Vanishing Polynomials • Vanishing Polynomial f(x) Z 2 m[X], x Z 2 m f(x)=0 • f(x), g(x) Z 2 m[X] if(f-g): vanishing means that 2 m | (f-g) • n! divides a product of n consecutive numbers 4! divides 99 X 100 X 101 X 102 • Find least n 2 m|n! Smarandache Function (SF) SF(23) = 4, since 23|4! 2 m divides the product of n = SF(2 m) consecutive numbers

Basic Number Theory • Let f(x), g(x) Z 23 [X], if (f-g): vanishing (1)23|(f - g) in Z 23 (2) 23|4! (3) 4! divides the product of 4 consecutive numbers (4) x Z 23, 4!|(x+1)(x+2)(x+3)(x+4) • Write (f-g) as a product of SF(2 m) = n consecutive numbers

Basis for factorization ØY 0(x) = 1 ØY 1(x) = (x + 1) ØY 2(x) = (x + 1)(x + 2) : Product of 2 consecutive numbers ØY 3(x) = (x + 1)(x + 2)(x + 3) : Product of 3 consecutive numbers Ø… Ø… ØYn(x) = Yn-1(x) (x + n) : Product of n consecutive numbers

Basis for factorization • Theorem 2: Sn(x) is vanishing in Z 2 m[X], where n = SF(2 m). • Example: • f = x 4 +2 x 3 + 3 x 2 + 2 x Z 23 [X]; SF(23) = 4 • f can be written as a product of 4 consecutive numbers. f= (x+1)(x+2)(x+3)(x+4) = Y 4(x) • f is a vanishing polynomial.

Constraints on the Coefficient • Example: • h(x) = 4 x 2 + 4 x = 4(x+1)(x+2) = 4 S 2(x) Z 23[X]; SF(23) = 4 • h(x) =0 x Z 23 • h is a vanishing polynomial. • But h(x) not equal to S 4(x) • Theorem 3: 2 m/gcd(k!, 2 m) Yk(x)=0 in Z 2 m[X], 0 k SF(2 m), 2 m/gcd(k!, 2 m) 為使 2 m/gcd(k!, 2 m) Yk(x)=0之min NOTE: b Yk(x)=0 in Z 2 m[X] 2 m/gcd(k!, 2 m) |b

Constraints on the Coefficient • Example: • h(x) = 4 x 2 + 4 x = 4(x+1)(x+2) = 4 Y 2(x) Z 23[X] • 23/gcd(2!, 23) | 4 • h is a vanishing polynomial.

Deciding Vanishing Polynomials • Theorem 4: • Let F be a polynomial in Z 2 m[X]. Then F is vanishes F = Fn. Yn + k=0 Σn-1 ak bk Yk Theorem 2 Theorem 3 Øn = SF(2 m), i. e. the least n such that 2 m|n! ØFn is an arbitrary polynomial in Z 2 m[x] Øak is an arbitrary integer Øbk = 2 m/gcd(k!, 2 m)

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

Algorithm Procedure zero_Identifi(polynomial, 2 m) 1. Calculate n = SF(2 m) 2. k = n: Reduce according to Throrem 2 Divide by Sn If remainder is zero, then F = Fn. Yn, else Continue

Algorithm 3. Reduce according to Theorem 3. Divide by Yn-1 to Y 0 Check if quotient is a multiple of bk = 2 m/gcd(k!, 2 m) If remainder is zero, then stop. else continue

Example 1 p= 4 x 2 + 4 x in Z 23 1. n = SF(23) = 4 2. k = 4: Divide by Y 4 deg(p) = 2< deg(Y 4)= 4 quo = 0, rem = 4 x 2 + 4 x F 4 = 0; Continue 3. k = 3: Divide by S 3 deg(p) = 2<deg(S 3) = 3 quo= 0, rem = 4 x 2 + 4 x continue 4. k = 2: Divide by Y 2 quo = 4; rem = 0 b 2 = 23/gcd(2!, 23) = 4 a 2 = quo/ b 2 =1 Z p is a vanishing polynomial in Z 23

Example 2 p= 5 x 2 + 3 x + 7 in Z 23 1. n = SF(23) = 4 3. k = 3: Divide by Y 3 deg(p) = 2<deg(Y 3) = 3 quo= 0, rem = 5 x 2+3 x + 7 continue 2. k = 4: Divide by Y 4 deg(p) = 2< deg(Y 4) = 4 quo = 0, rem=5 x 2+3 x + 7 4. k = 2: Divide by Y 2 quo = 5; rem = 4 x+5 F 4 = 0; Continue b 2 = 23/gcd(2!, 23) = 4 a 2 = quo/ b 2 =5/4 Z p is not a vanishing polynomial in Z 23

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

Multiple Polynomial • Definition: • (1) Let R be a ring, define the ring R[x 1, …, xn ] of polynomial in the indeterminates x 1, …, xn recursively as follows: R[x 1, …, xn ] = (R[x 1, …, xn-1])[xn] • (2) x 1 i 1…xnin is called monomial , ax 1 i 1…xnin is called monomial term, where a為此term之coefficient • (3) The degree of x 1 i 1…xnin is (i 1, …, in) n denote deg(x 1 i 1…xnin)

Multiple Polynomial If R is a commutative and f(x 1, …, xn) R[x 1, …, xn ], then the mapping : R R given by (a 1, …, an) The mapping is called polyfunction. In this problem, : Z 2 n 1 … Z 2 nd Z 2 m • Definition: Let k=(k 1, k 2, …, kd) n, we define Yk=yk 1(x 1)…ykd(xd), where yki(xi) is the falling factor of degree ki in xi

Example • F(x 1, x 2)=x 14 x 2 + 2 x 13 x 2+ 3 x 12 x 2+ 2 x 1 x 2 over Z 22[x 1, …, xn ] 1. sf(22)=4 2. F=Y(4, 1) (x 1, x 2)=Y 4(x 1)Y 1(x 2)=0 in Z 22 • We wish to generalize these results to analyze polyfunctions over Z 2 n 1 … Z 2 nd Z 2 m

Lemma 8 (1) Z 2 then Y 2 ni (xi)=0, i=1, 2, …, d (2)Let n=sf(2 m) then Yn(x)=0 Take i=min{2 ni, sf(2 m)} , i=1, 2, …, d then Y i Z 2 is vanshing polynomial ni ni • Lemma: Let k=(k 1, k 2, …, kd) n, then Yk=0 ki i, for some i

Example • F(x 1, x 2)=x 12 x 2 - x 1 x 2 be a polynomial corresponding to the polyfunction : Z 21 Z 22 Z 23. We show that F is a vanshing polynomial. 1. sf(23)=4, 1=2, 2=4 2. x 12 x 2 - x 1 x 2 =x 1(x 1 -1) x 2=Y(2, 1) (x 1, x 2) 3. k 1 1=2 The condition in lemma is satisfied, Hence F is vanshing polynomial

Constraints on the Coefficient • Theorem 8: • The expression ck Yk=0 in Z 2 m[X] d 2 m/gcd( i=1 ki!, 2 m) | ck ¨ck Z 2 m ¨k=(k 1, k 2, …, kd) n such that ki i, i=1, 2, …, d

Example • F(x 1, x 2)=4 x 1 x 22 + 4 x 1 x 2 be a polynomial corresponding to the polyfunction : Z 21 Z 22 Z 23. We show that F is a vanshing polynomial. 1. 2 n 1=2, 2 n 2=4, sf(23)=4, 1=2, 2=4, 2. 4 x 1 x 22 + x 1 x 2 =4 x 1 x 2 (x 1 -1) = c(1, 2) Y(1, 2) (x 1, x 2) 3. 8/gcd( 1!x 2!, 8) | c(1, 2)且k 1 1=2, k 2 2=4 The condition in lemma is satisfied, Hence F is vanshing polynomial

Deciding Vanishing Polynomials • Theorem: Let F be a polynomial representation for the functiond from Z 2 n 1 … Z 2 nd to Z 2 m. Then F is vanishes F = i=1 Qi. Y (i) + Σakbk. Yk Lemma 8 Theorem 8 Øn = SF(2 m), i. e. the least n such that 2 m|n! Øk=(k 1, k 2, …, kd) n, for each ki=1, 2, …, i ØY (i) is falling factor of degree i ØQi is an arbitrary polynomial Øak is an arbitrary integer Øbk = 2 m/gcd(k!, 2 m)

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

Example

Outline • Introduction • Modeling • Univariate Vanishing Polynomials • Algorithm of Univariate • Multi-varite Vanishing Polynomials • Algorithm of Multi-varite • Conclusions and Future Work

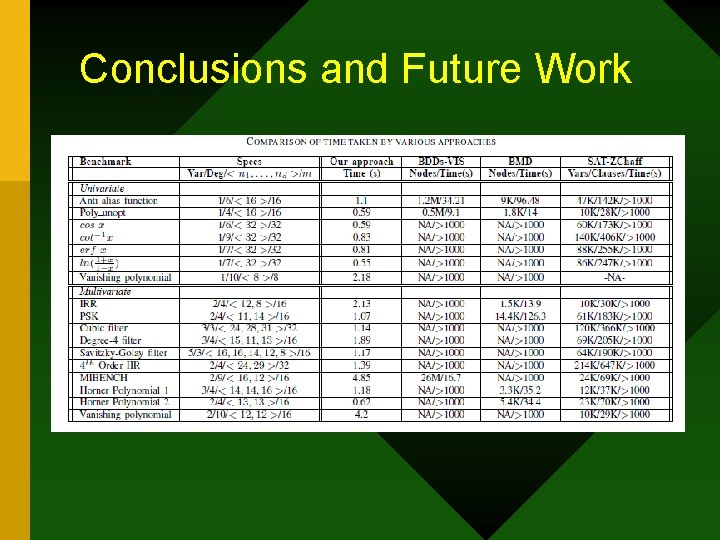
Conclusions and Future Work

Thank You