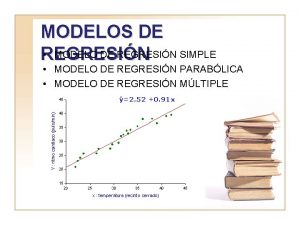
DERIVADO DE LOS COEFICIENTES DE REGRESIN LINEAL Y













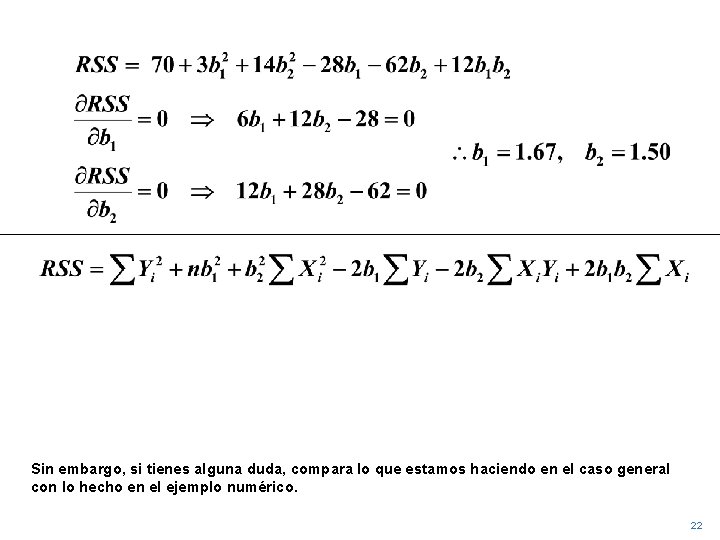
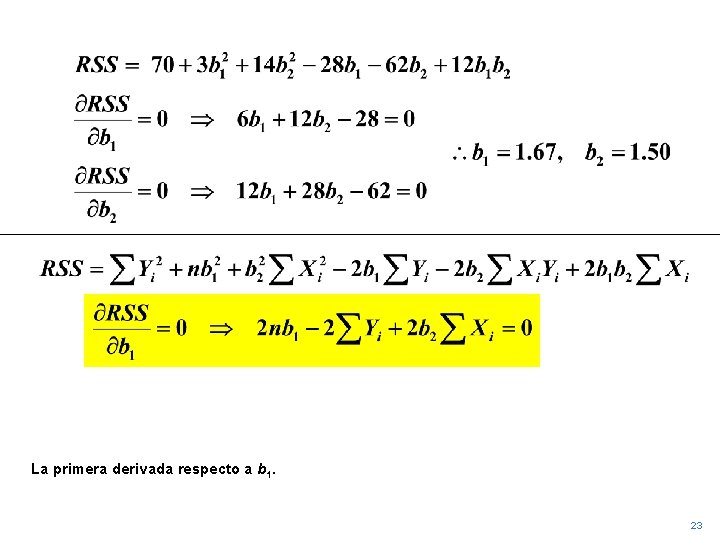

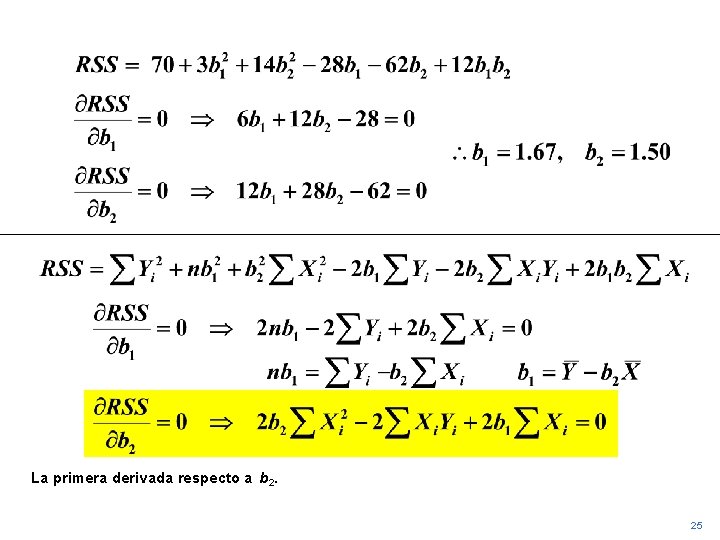
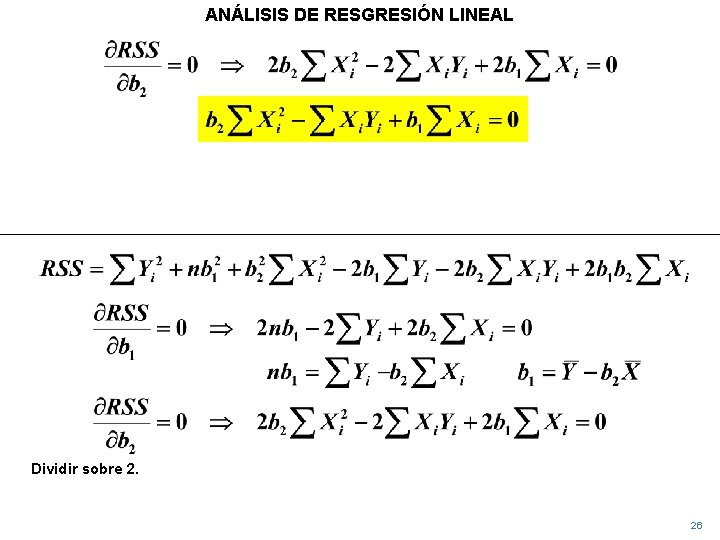

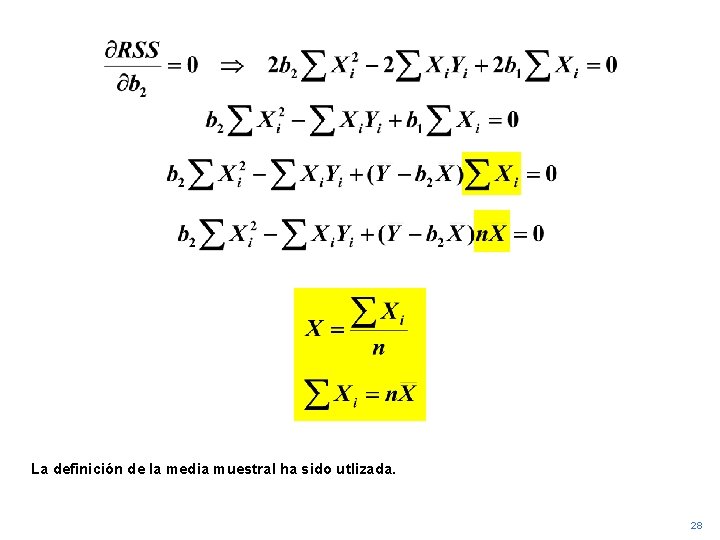
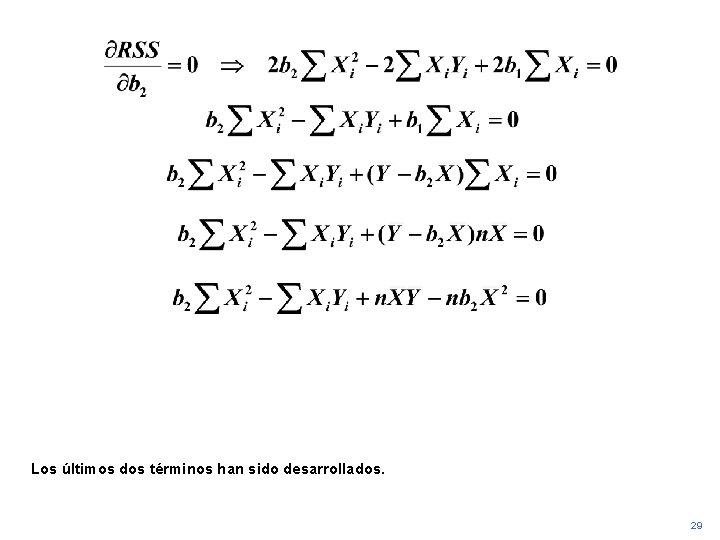
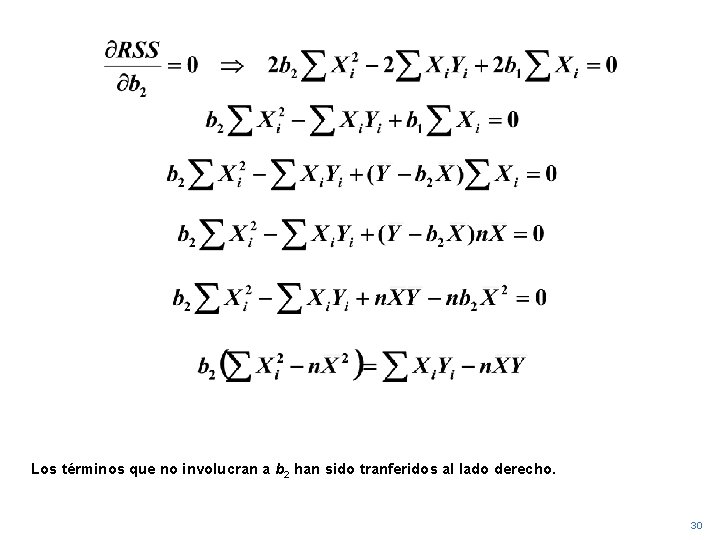









- Slides: 41

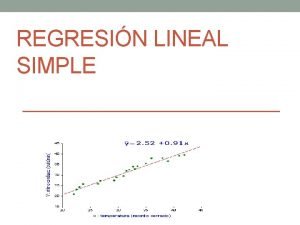
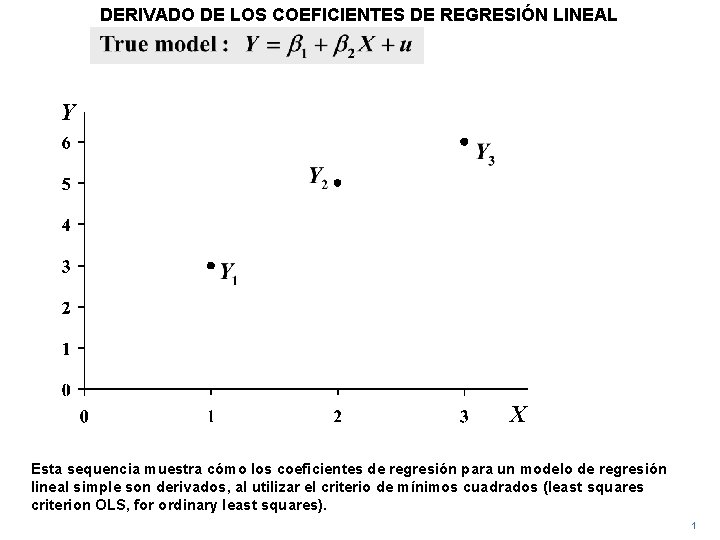
DERIVADO DE LOS COEFICIENTES DE REGRESIÓN LINEAL Y X Esta sequencia muestra cómo los coeficientes de regresión para un modelo de regresión lineal simple son derivados, al utilizar el criterio de mínimos cuadrados (least squares criterion OLS, for ordinary least squares). 1

Y X Comenzaremos con un ejemplo númerico con sólo tres obervaciones: (1, 3), (2, 5), y (3, 6). 2

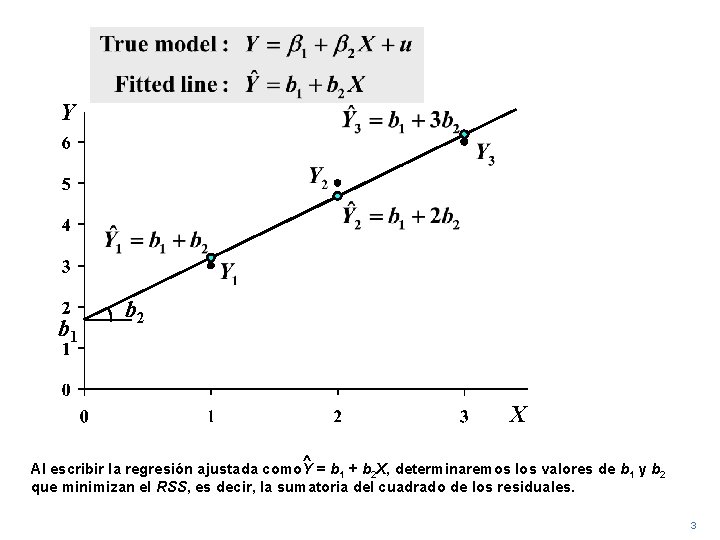
Y b 1 b 2 X ^ Al escribir la regresión ajustada como. Y = b 1 + b 2 X, determinaremos los valores de b 1 y b 2 que minimizan el RSS, es decir, la sumatoria del cuadrado de los residuales. 3

Y b 1 b 2 X Dada la elección de b 1 y b 2, los residuales son los siguientes. 4

ANÁLISIS DE REGRESIÓN SIMPLE La sumatoria del cuadrado de los residuales es, por lo tanto, la que se muestra arriba. 5

Los cuadráticos han sido desarrollados. 6

La ecuación ha sido simplicada al juntar los términos similares. 7

Para un mínimo, las derivada parciales de RSS respecto a b 1 y b 2 deben ser cero. (También debemos checar las condiciones de segundo orden). 8

Las condiciones de primer orden nos dan dos ecuaciones con dos incognitas. 9

Al resolver el sistema de ecuaciones, encontramos que RSS es minimizado cuando b 1 y b 2 son iguales a 1. 67 y 1. 50, respectivamente. 10

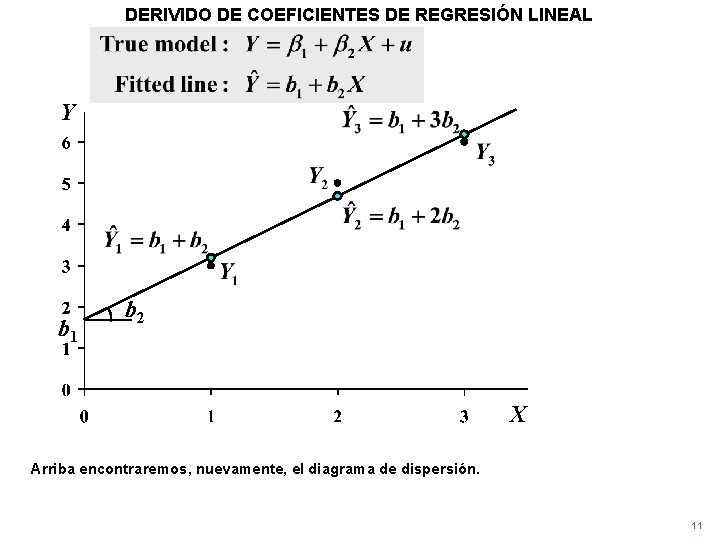
DERIVIDO DE COEFICIENTES DE REGRESIÓN LINEAL Y b 1 b 2 X Arriba encontraremos, nuevamente, el diagrama de dispersión. 11

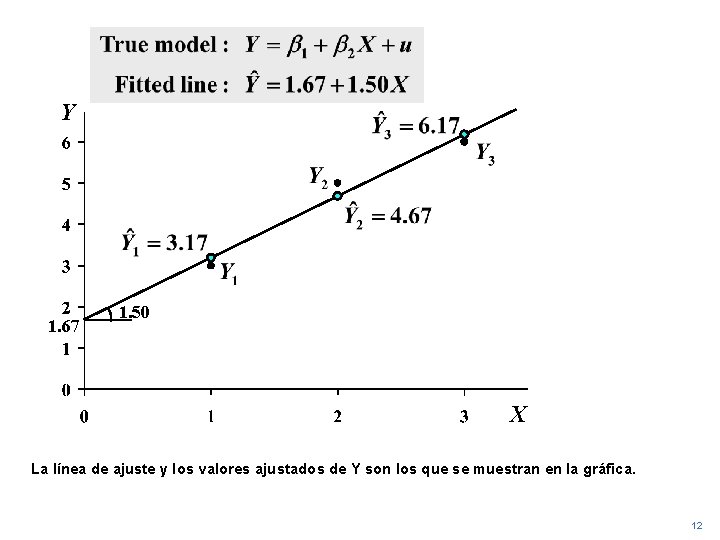
Y 1. 67 1. 50 X La línea de ajuste y los valores ajustados de Y son los que se muestran en la gráfica. 12

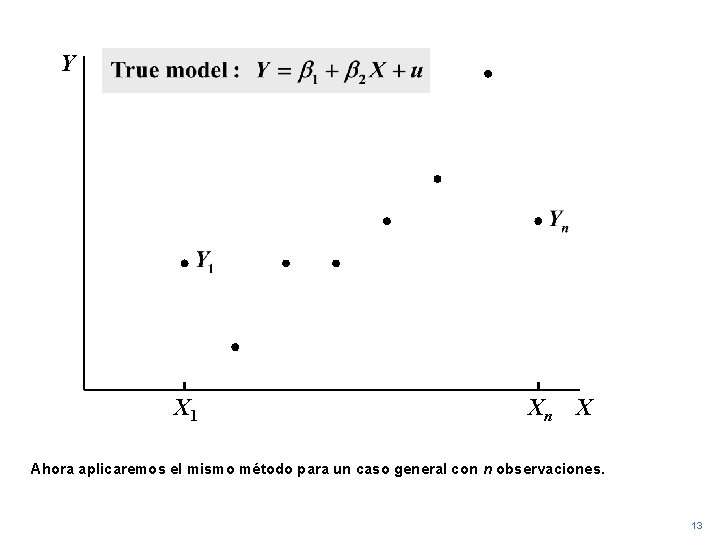
Y X 1 Xn X Ahora aplicaremos el mismo método para un caso general con n observaciones. 13

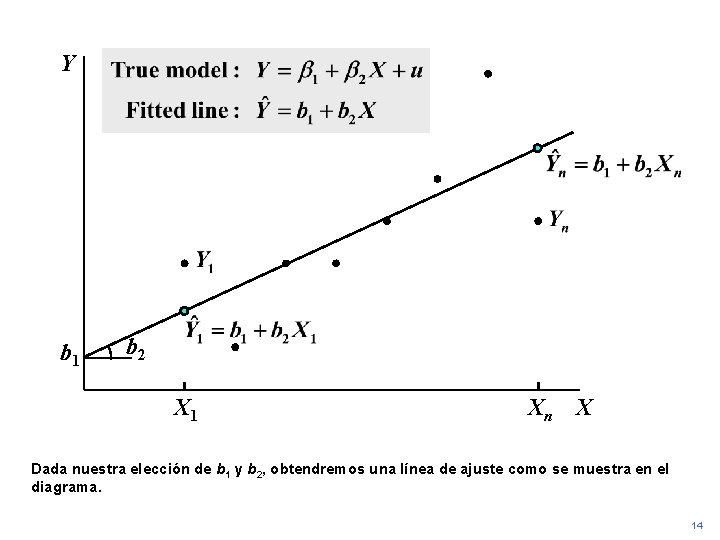
Y b 1 b 2 X 1 Xn X Dada nuestra elección de b 1 y b 2, obtendremos una línea de ajuste como se muestra en el diagrama. 14

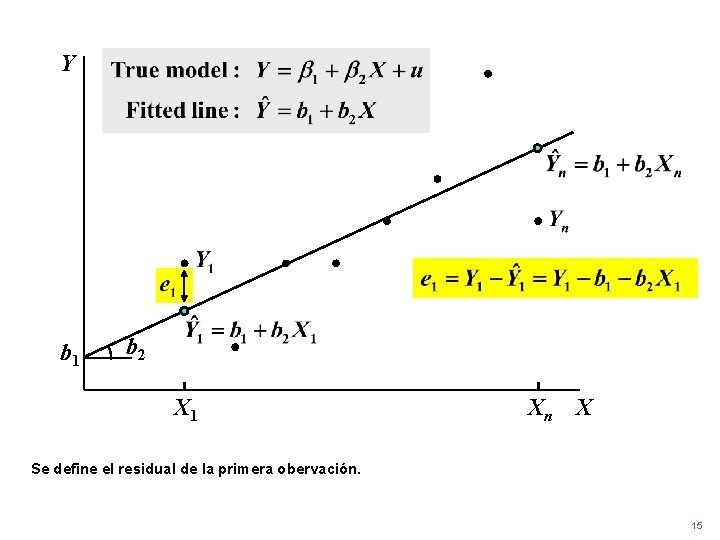
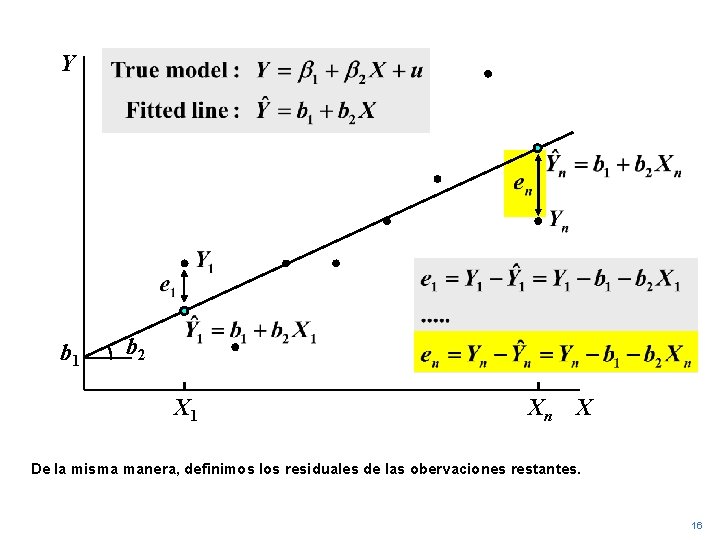
Y b 1 b 2 X 1 Xn X Se define el residual de la primera obervación. 15

Y b 1 b 2 X 1 Xn X De la misma manera, definimos los residuales de las obervaciones restantes. 16

La RSS, la sumatoria del cuadrado de los residuales, es definida para el caso general. Los datos de ejemplo númerico se muestran para una comparación. 17

Los cuadráticos son desarrollados. 18

Se juntan los términos similares. 19

Notese que en esta ecuación las observaciones de X y Y son sólo datos que determinan los coeficientes en la ecuación de la RSS. 20

La elección de variables en la ecuación son b 1 y b 2. Esto puede parecer un poco extraño porque en los cursos introductorios de cálculo b 1 y b 2 son usualmente constantes y X y Y son variables. 21
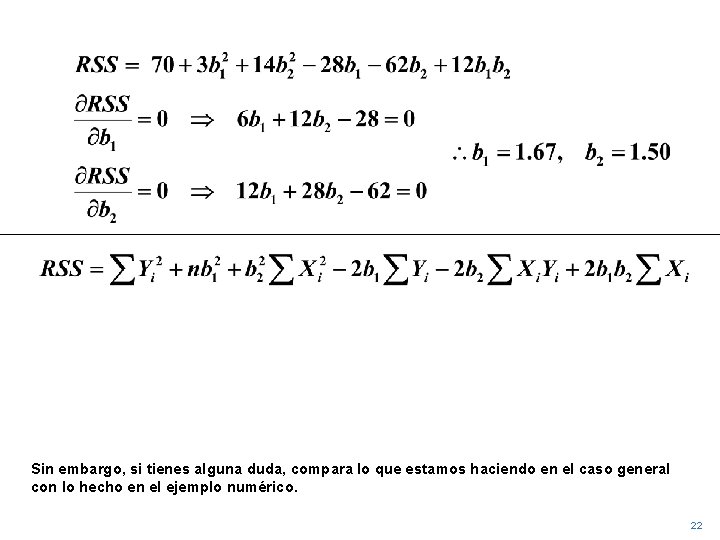
Sin embargo, si tienes alguna duda, compara lo que estamos haciendo en el caso general con lo hecho en el ejemplo numérico. 22
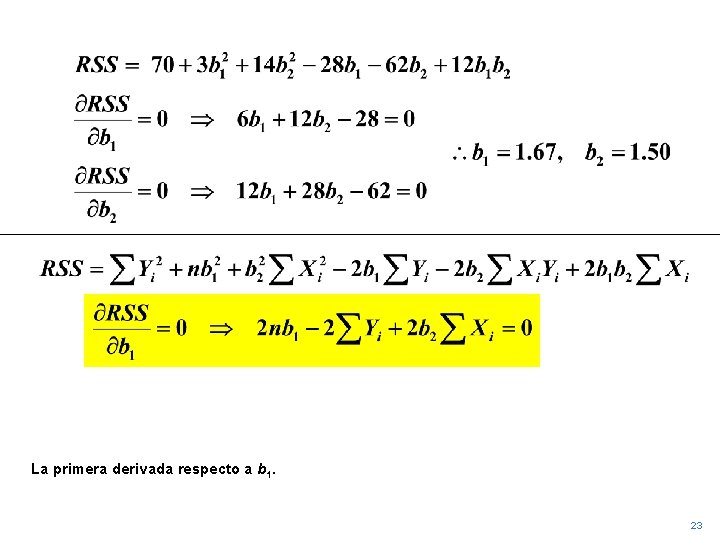
La primera derivada respecto a b 1. 23

Con una simple manipulación, obtenemos una expresión simplicada de b 1. 24
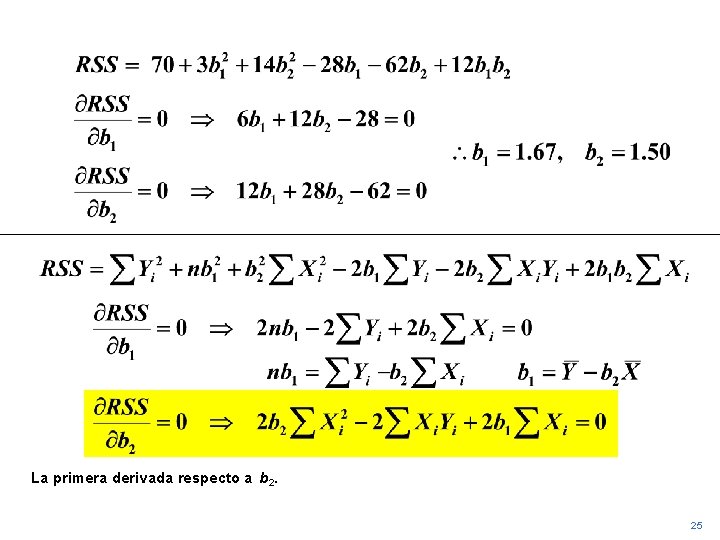
La primera derivada respecto a b 2. 25
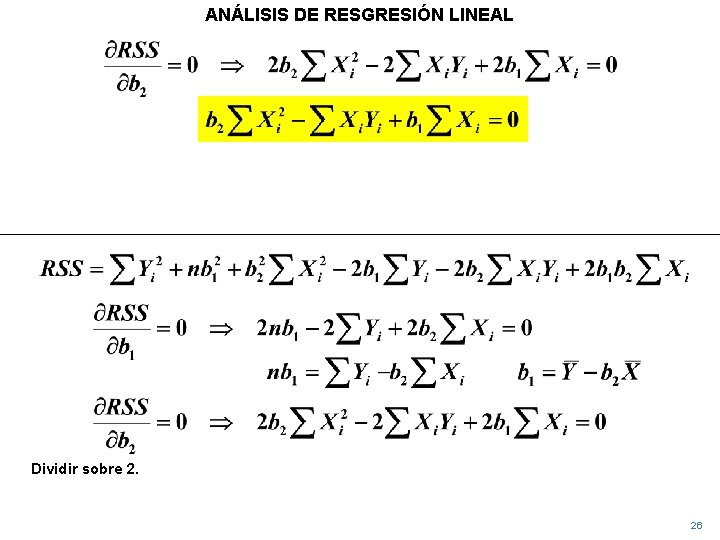
ANÁLISIS DE RESGRESIÓN LINEAL Dividir sobre 2. 26

Ahora subtituimos b 1 al utilizar la expresión obtenida para ello y como resultado obtenemos una ecuación que contiene solamente a b 2. 27
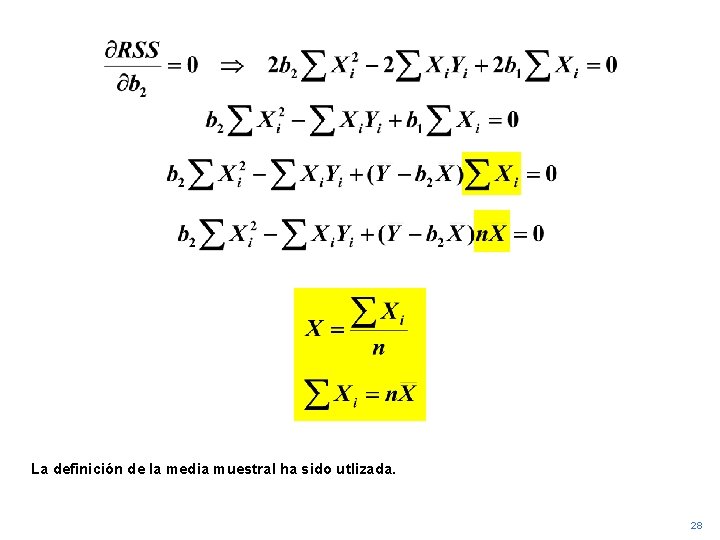
La definición de la media muestral ha sido utlizada. 28
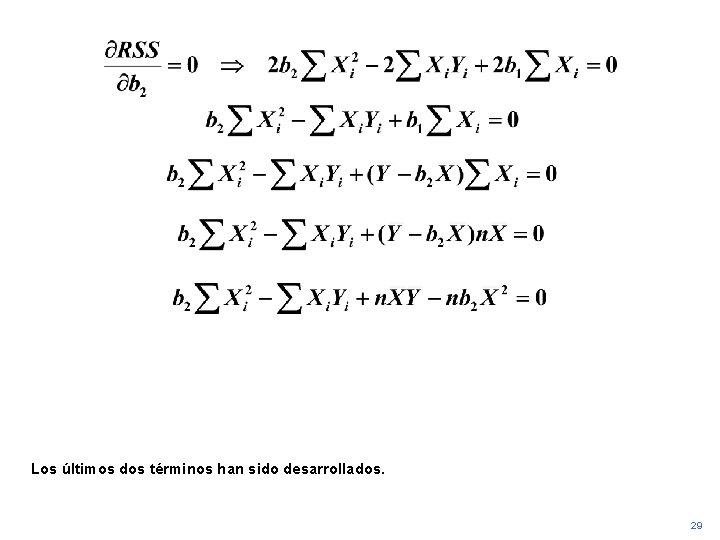
Los últimos dos términos han sido desarrollados. 29
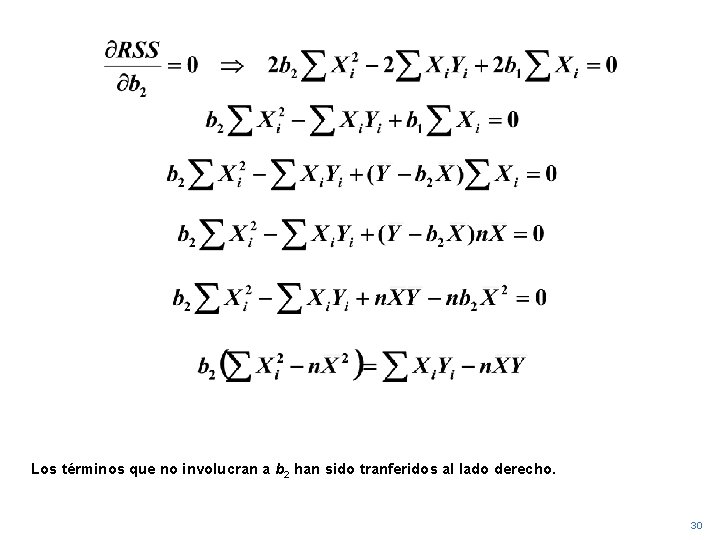
Los términos que no involucran a b 2 han sido tranferidos al lado derecho. 30

Para crear espacio, la ecuación ha sido colocada en la parte superior de la diapositiva. 31

SIMPLE REGRESSION ANALYSIS Ahora, obtenemos una expresión para b 2. 32

En la práctica debemos utilizar una expresión alternativa. A continuación, demostraremos que son equivalentes. 33

Al expandir el numerador, obtenemos los términos mostrados. 34

En el segundo término el valor medio de Y (mean value of Y) es un facotr común. En el tercero, el valor medio de X es un facotr común. El último término es el mismo para todas las i. 35

Utilizamos la definición de la media muestral para simplificar la expresión. 36

Por lo tanto, hemos demostrado que los numeradores de ambas expresiones son iguales. 37

El denominador es matematicamente un caso especial del numerador, al remplazar Y por X. Por lo tanto, las expresiones son equivalentes. 38

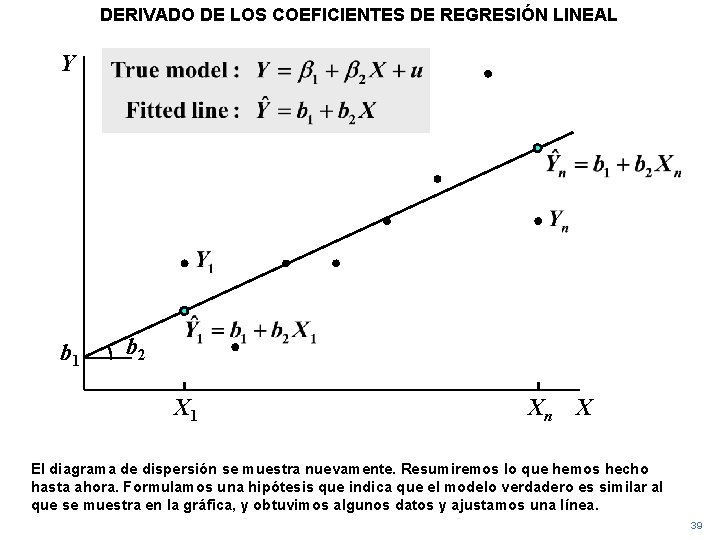
DERIVADO DE LOS COEFICIENTES DE REGRESIÓN LINEAL Y b 1 b 2 X 1 Xn X El diagrama de dispersión se muestra nuevamente. Resumiremos lo que hemos hecho hasta ahora. Formulamos una hipótesis que indica que el modelo verdadero es similar al que se muestra en la gráfica, y obtuvimos algunos datos y ajustamos una línea. 39

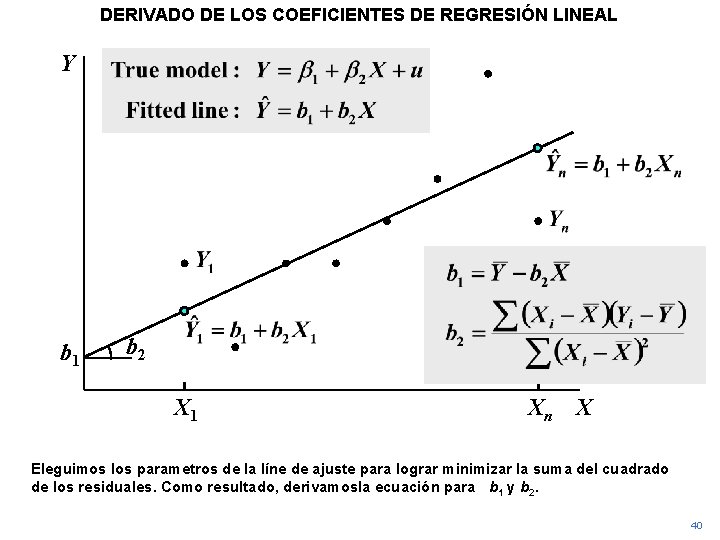
DERIVADO DE LOS COEFICIENTES DE REGRESIÓN LINEAL Y b 1 b 2 X 1 Xn X Eleguimos los parametros de la líne de ajuste para lograr minimizar la suma del cuadrado de los residuales. Como resultado, derivamosla ecuación para b 1 y b 2. 40

Copyright Christopher Dougherty 1999– 2006. This slideshow may be freely copied for personal use. 17. 06
 Ecuación lineal
Ecuación lineal Coeficientes indeterminados
Coeficientes indeterminados Simplex tabular
Simplex tabular Derivado vegetal
Derivado vegetal Poder constituinte originário e derivado
Poder constituinte originário e derivado Derivado del ectodermo
Derivado del ectodermo Poder constituinte originário e derivado
Poder constituinte originário e derivado Poder constituinte originário e derivado
Poder constituinte originário e derivado Relacionamento ternário
Relacionamento ternário Derivada 1/x
Derivada 1/x Poder constituinte originário e derivado
Poder constituinte originário e derivado Asteniz
Asteniz Derivadas de paz
Derivadas de paz Que es un organo administrativo
Que es un organo administrativo Ferreiro é um substantivo derivado
Ferreiro é um substantivo derivado Ismo sufijo
Ismo sufijo Coeficientes indeterminados
Coeficientes indeterminados Binmio
Binmio Coeficientes de butterworth
Coeficientes de butterworth Una expresión algebraica es una combinación de
Una expresión algebraica es una combinación de Coeficientes numericos ejemplos
Coeficientes numericos ejemplos Rfrrrrrrrrr
Rfrrrrrrrrr Monomio simetrico
Monomio simetrico Ejercicios potencias primero medio
Ejercicios potencias primero medio Regresion multiple en spss
Regresion multiple en spss Analizs
Analizs Regresin
Regresin Regresin
Regresin Regresin
Regresin Regresin
Regresin Tabla de contingencia bidimensional
Tabla de contingencia bidimensional Regresin
Regresin Regresin
Regresin Regresin
Regresin Regresin
Regresin Regresin
Regresin Regresin
Regresin Regresin
Regresin Regresion multiple en spss
Regresion multiple en spss Ecuacion de regresion
Ecuacion de regresion Regresin
Regresin Regresion logistica
Regresion logistica