Filtros Ativos Clculo dos Coeficientes dos Filtros de

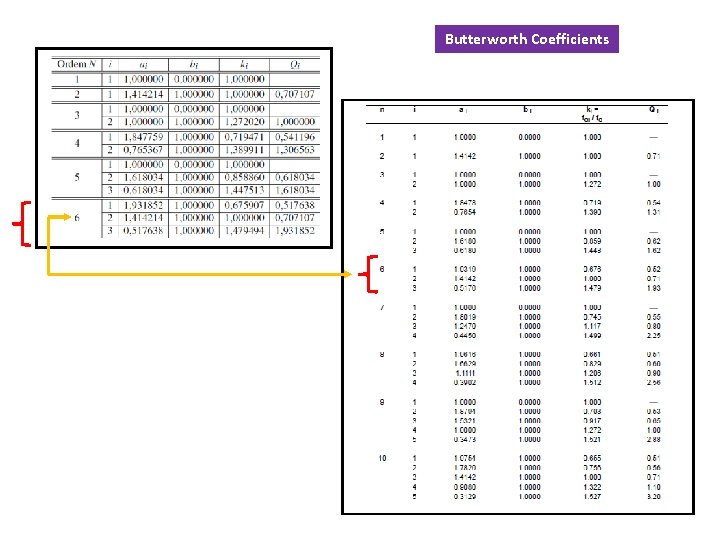
Filtros Ativos Cálculo dos Coeficientes dos Filtros de Butterworth

Para a implementação prática de um filtro racional H(s) de ordem N com ganho unitário do tipo fatora-se a função de transferência H(s) como: A equação pode ser reescrita: sendo

Cada filtro Hi(s) apresenta uma frequência de corte wci que não é necessariamente igual à frequência de corte wc do filtro H(s). Define-se a razão entre estas duas frequências Para filtros de ordem 2 também é possível se definir o fator de qualidade que representa a seletividade. Na prática é importante montar os filtros que compõem H(s) em ordem crescente de fator de qualidade (Qi) para evitar que ocorra saturação na saída dos amplificadores operacionais que compõem o filtro.

Para aproximar a função de transferência ideal um filtro de Butterworth tenta manter a banda de passagem o mais plana possível. A amplitude da sua função de resposta em frequência |H( jw)| é definida por: em que N é a ordem do filtro. Quanto maior o valor de N, mais o filtro de Butterworth se aproxima das características ideais.

Para um filtro de Butterworth pode-se escrever: Os seus pólos são raízes da equação: Esta equação possui 2 N raízes complexas. Para que o filtro de Butterworth seja estável seus pólos devem estar localizados no semi-plano complexo esquerdo aberto. Utiliza-se as N raízes complexas da equação que estão situadas nesse semi-plano.

Cálculo das raizes da equação :

Multiplicando-se os dois lados da equação acima por -1, que é igual a ejπ , obtem-se:

Esta expressão corresponde a 2 N números complexos distintos sobre o círculo unitário do plano complexo. Por exemplo, para N = 5 :

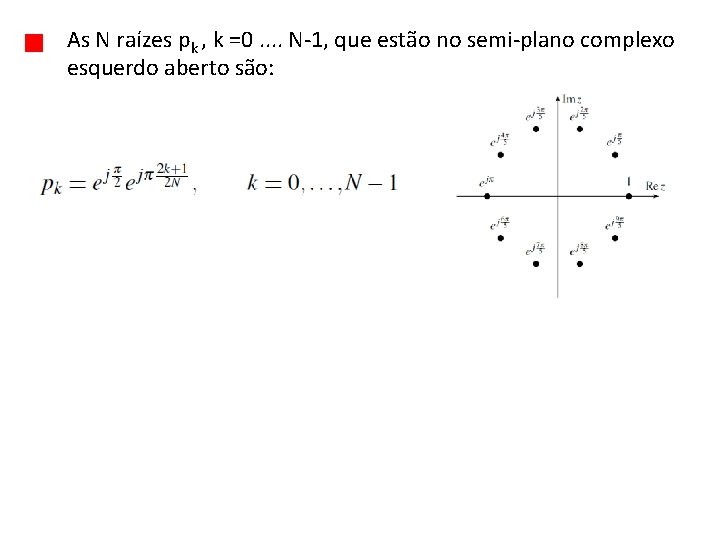
As N raízes pk , k =0. . N-1, que estão no semi-plano complexo esquerdo aberto são:

Para N = 5, que corresponde as raízes situadas no semi-plano complexo esquerdo aberto. , Os valores pk são portanto os pólos do filtro de Butterworth, e sua funçãode transferência pode ser escrita como:

A função de transferência acima não está fatorada na forma Na prática os coeficientes ai e bi são calculados a partir dos valores de capacitância e resistência que implementam o filtro, dependendo da topologia de implementação escolhida, de forma que ai e bi são sempre números reais, enquanto que 1 -s/pk pode ser um polinômio com coeficientes complexos não reais quando pk não é real.

É necessário agrupar os pares de polos complexos conjugados na expressão acima para obter uma função de transferência na forma em que todos os ai e bi são reais.

Exemplo 1: N=5 Como , em que z nota o complexo conjugado de z, pode se reescrever:

Exemplo 1: N=5 Usando que p 2 = -1,

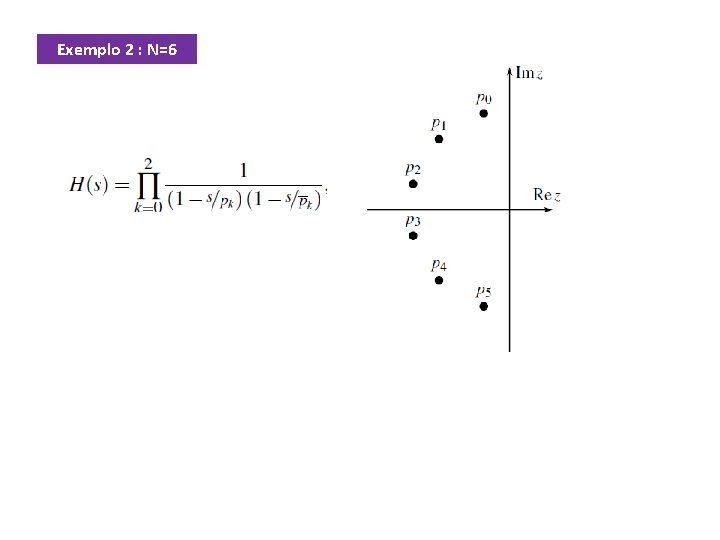
Exemplo 2 : N=6 No caso N = 6, ocorre uma situação similar, em que pode-se escrever: A diferença é que não aparece o termo 1/(1+s) por não haver nenhum pólo sobre o eixo real, como era o caso de p 2 quando N = 5.

Exemplo 2 : N=6

Os exemplos com N = 5 e N = 6 permitem compreender com mais facilidade o caso geral. N é impar Quando N é ímpar, há sempre um polo sobre o eixo real, que é o polo (p 2 = -1 no caso N = 5). O agrupamento dos demais pólos em pares de pólos complexos conjugados, da mesma forma que foi feito para o caso N = 5, fornece a expressão:

N é par Quando N é par não há pólos sobre o eixo real e o agrupamento dos pares de polos complexos conjugados fornece a expressão:

Filtros Ativos Cálculo dos Coeficientes de Butterworth Filtros de Butterworth Observa-se que: Como , reescreve-se:

Como tem-se: A função de transferência de um filtro de Butterworth de ordem N é dada por:

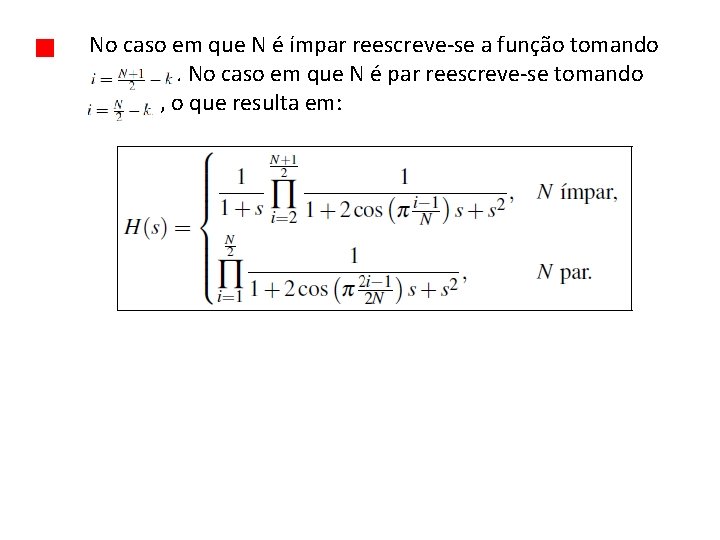
No caso em que N é ímpar reescreve-se a função tomando. No caso em que N é par reescreve-se tomando , o que resulta em:

O fator de qualidade Qi do filtro Para o filtro é . o fator de qualidade é

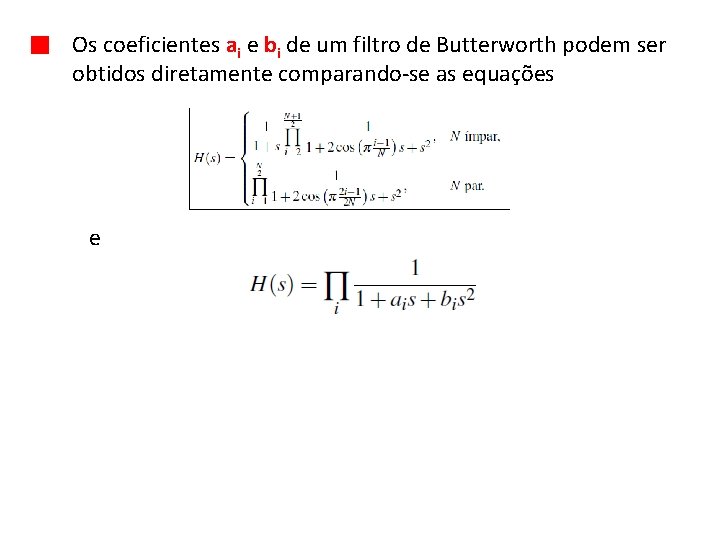
Os coeficientes ai e bi de um filtro de Butterworth podem ser obtidos diretamente comparando-se as equações e

Cálculo de ki Ki é a relação entre a frequência de corte do filtro i (wci), e a frequência de corte do filtro global (wc): A frequência de corte wci é definida como o valor w tal que

Cálculo de ki - Filtro de ordem 1 Logo, tem-se a solução de quando:

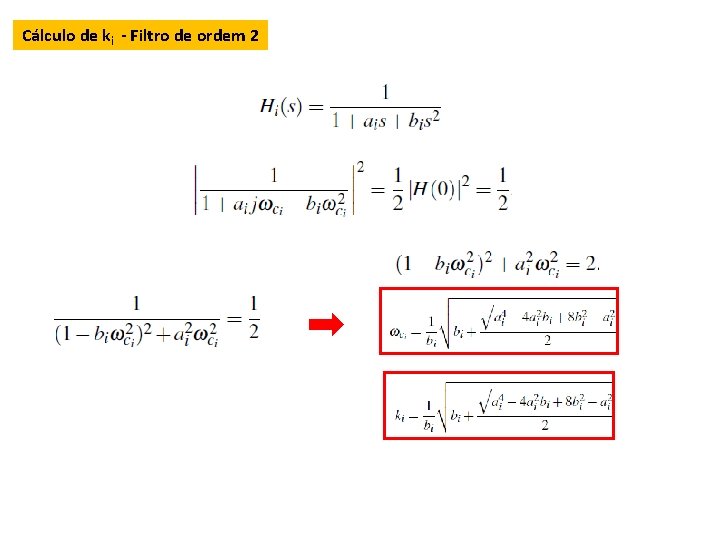
Cálculo de ki - Filtro de ordem 2

Butterworth Coefficients