Monmios e Polinmios Vamos considerar a figura 4







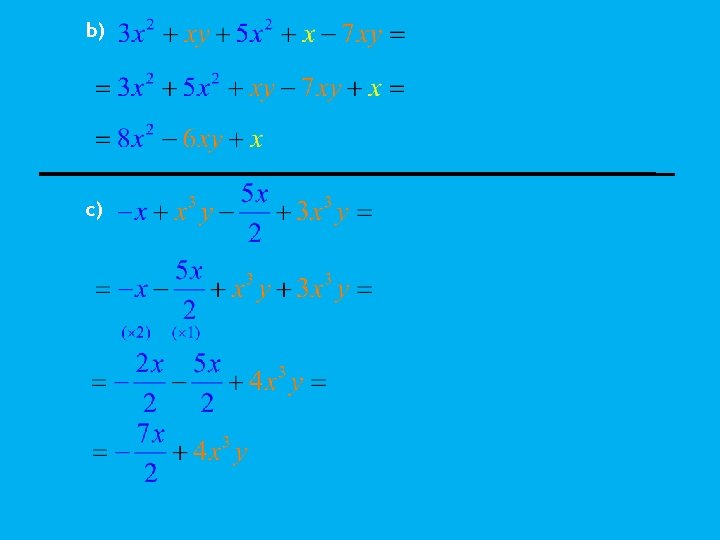
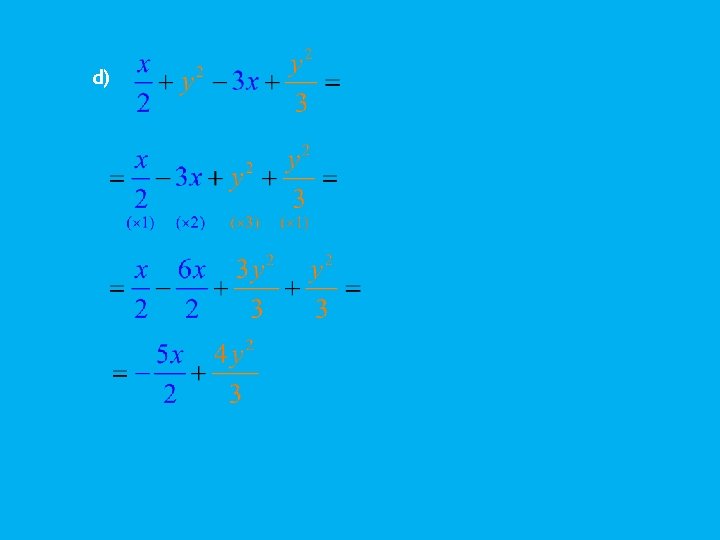



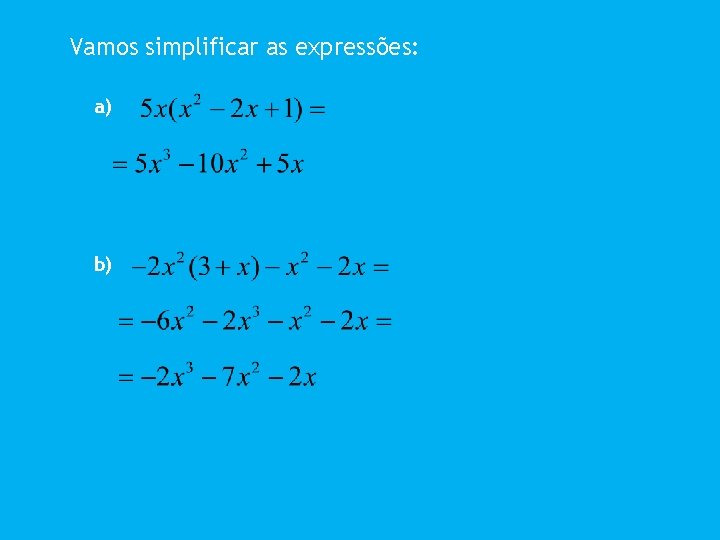






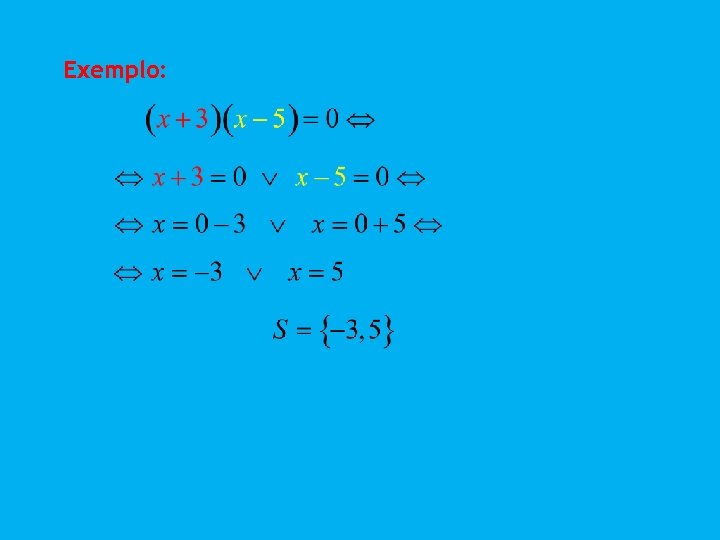
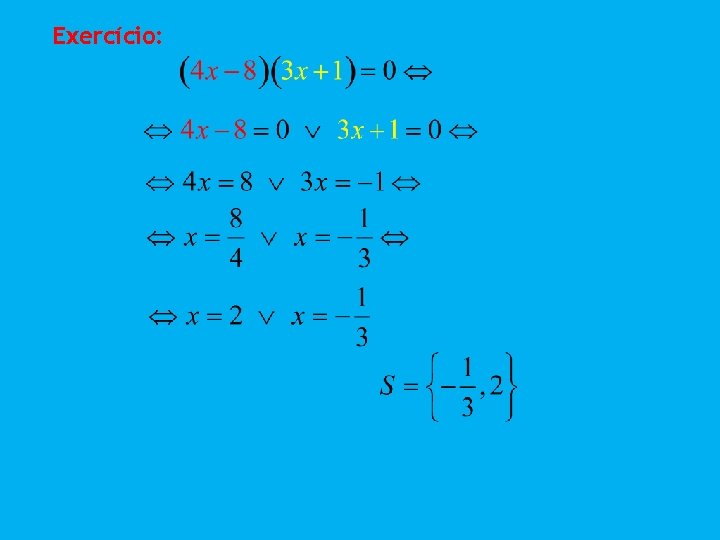





- Slides: 35

Monómios e Polinómios

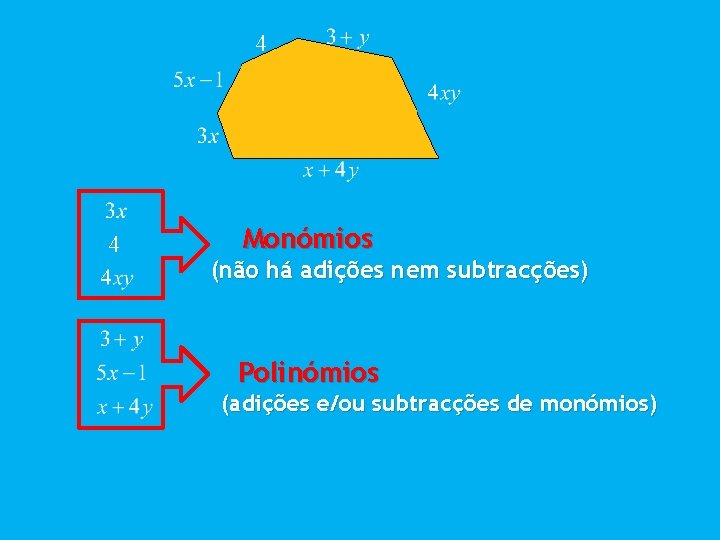
Vamos considerar a figura: 4 Para calcular o perímetro da figura vamos concretizar as variáveis x e y, fazendo e e. Perímetro 3 4 4 5 8 9 33

4 4 Monómios (não há adições nem subtracções) Polinómios (adições e/ou subtracções de monómios)

Definições: Um monómio é uma expressão onde não aparecem nem adições nem subtracções, ou seja, é um número ou uma letra ou um produto de um número e letras, estas com expoentes naturais. Outros exemplos de monómios: Um polinómio é a soma algébrica de monómios. Outros exemplos de polinómios:

Num monómio podemos distinguir uma parte numérica ou coeficiente e uma parte literal. Por exemplo: coeficiente parte literal Definições: Monómios Semelhantes são os que têm a mesma parte literal. Exemplos:

Monómios Simétricos são monómios semelhantes com coeficientes simétricos. Exemplos: Grau de um monómio é a soma dos expoentes das letras. Exemplos:

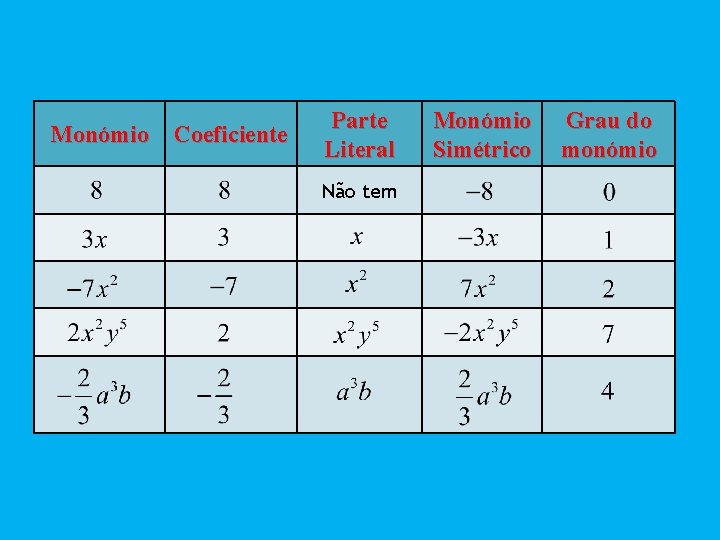
Monómio Coeficiente Parte Literal Não tem Monómio Simétrico Grau do monómio

Adição algébrica de monómios e polinómios 4 A expressão simplificada do perímetro da figura é:

Só podemos somar ou subtrair monómios semelhantes, ou seja, com a mesma parte literal. Vamos simplificar as seguintes expressões: a)
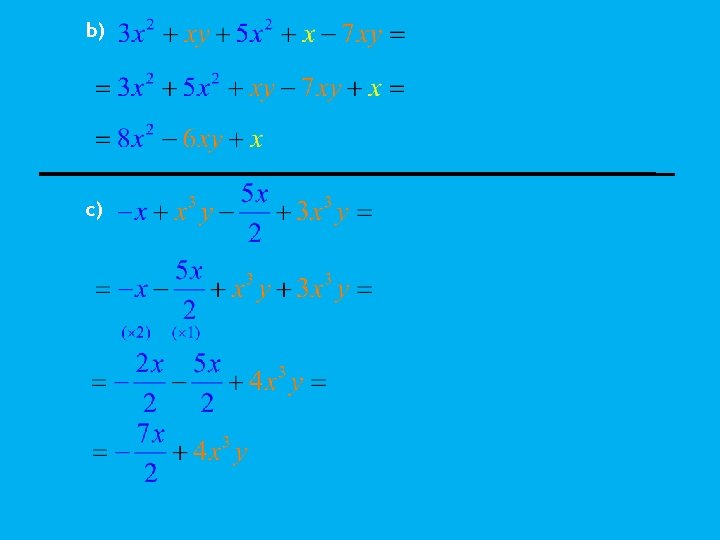
b) c)
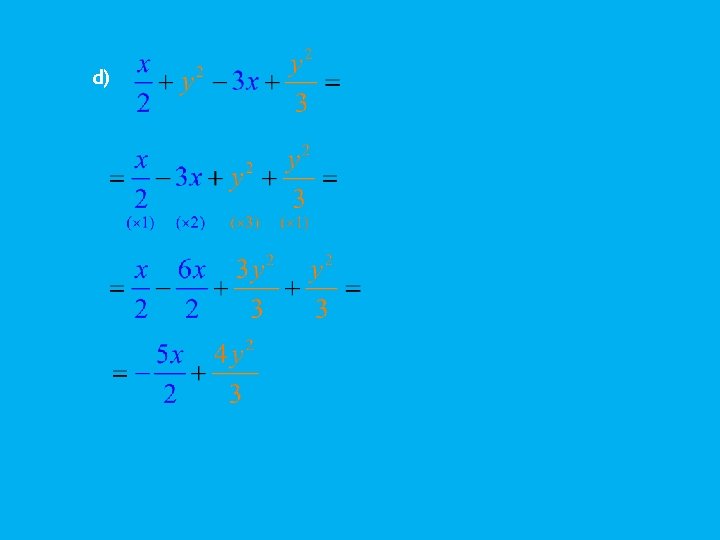
d)

Potência de um monómio A expressão da área do quadrado é:

Vamos calcular: a) b)

Produto de um monómio por um polinómio A expressão simplificada da área do rectângulo é:
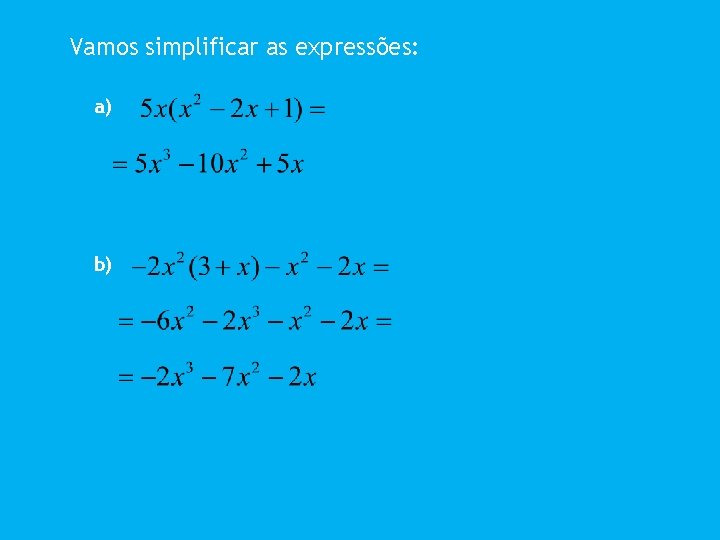
Vamos simplificar as expressões: a) b)

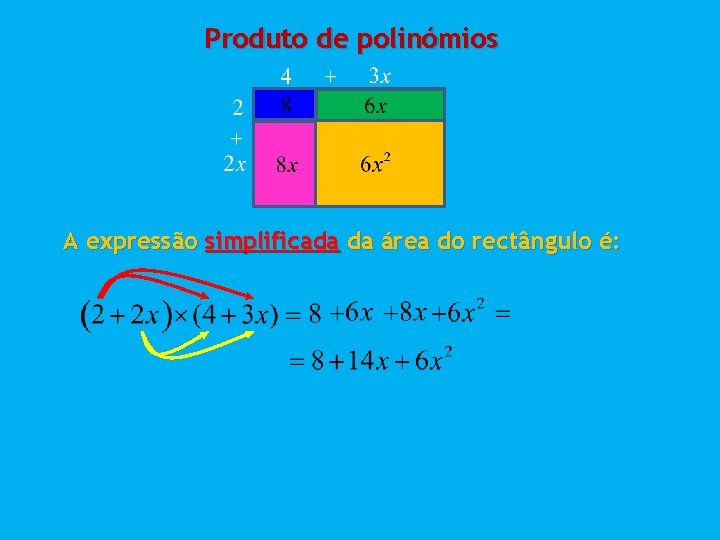
Produto de polinómios A expressão simplificada da área do rectângulo é:

Casos notáveis da multiplicação

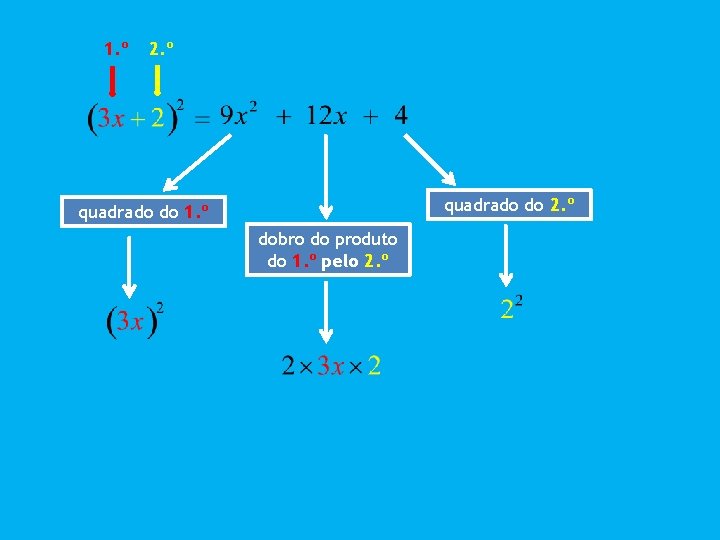
Fórmula do quadrado do binómio A expressão simplificada da área do quadrado é:

1. º 2. º quadrado do 1. º dobro do produto do 1. º pelo 2. º

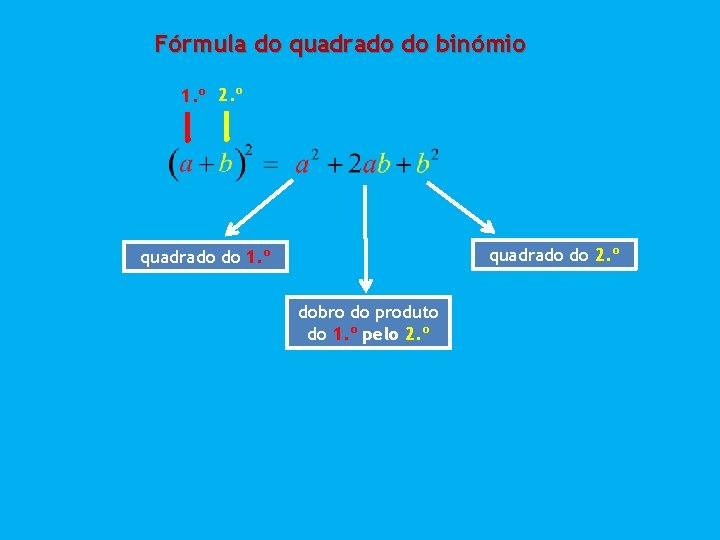
Fórmula do quadrado do binómio 1. º 2. º quadrado do 1. º dobro do produto do 1. º pelo 2. º

Calcula: a) b) c) d)

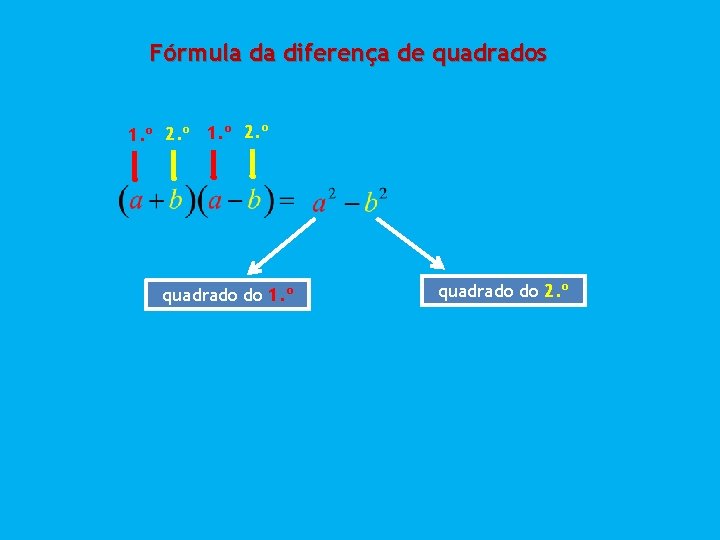
Fórmula da diferença de quadrados As duas figuras têm a mesma área:

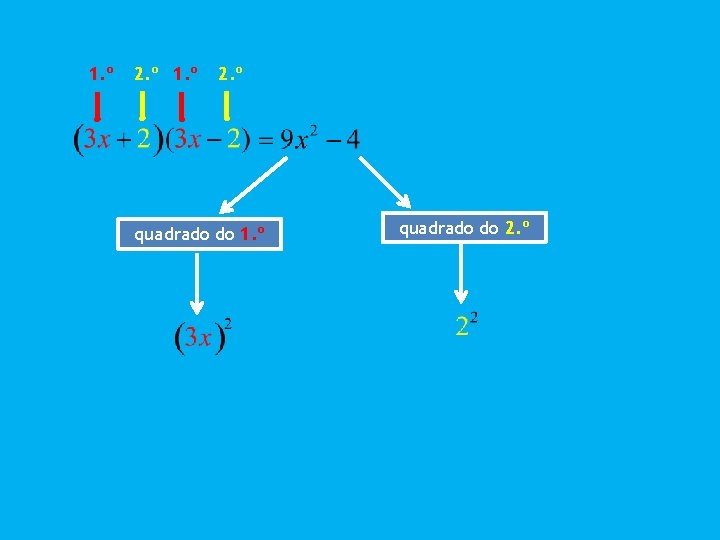
1. º 2. º quadrado do 1. º quadrado do 2. º

Fórmula da diferença de quadrados 1. º 2. º quadrado do 1. º quadrado do 2. º

Calcula: a) b) c) d)

Lei do anulamento do produto Um produto é igual a zero quando pelo menos um dos factores é zero, ou seja,
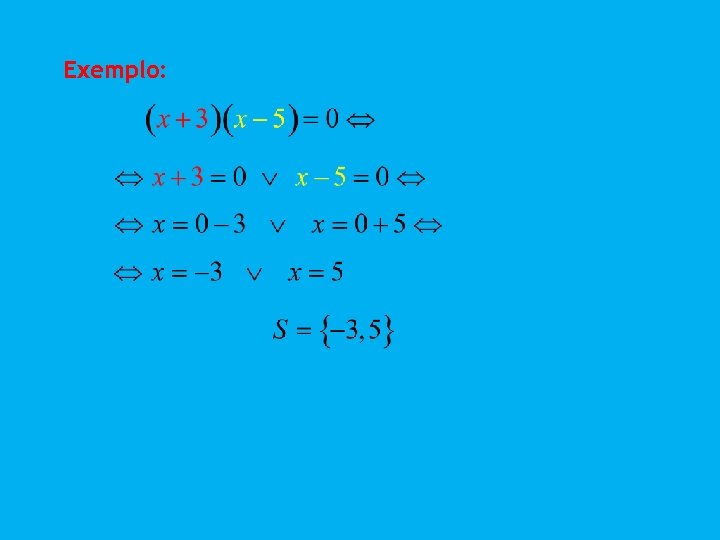
Exemplo:
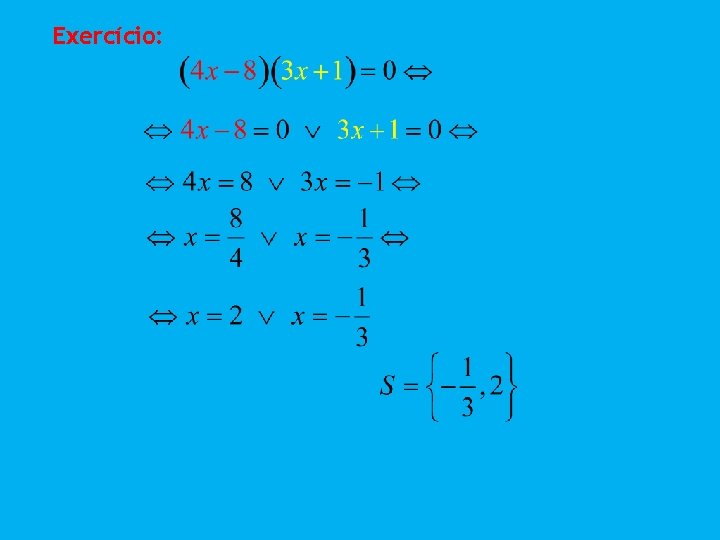
Exercício:

Equações de grau superior ao primeiro

Para resolvermos equações de grau superior ao primeiro vamos usar a lei do anulamento do produto, para isso temos que ter no 1. º membro um produto de factores e no 2. º membro zero. Nas equações seguintes (do 2. º grau) vamos começar por transformar o 1. º membro num produto de factores, ou seja, vamos factorizar o 1. º membro.

1. Em cada monómio do 1. º membro temos o x em comum, vamos colocá-lo em evidência. Aplicar a lei do anulamento do produto.

2. Não temos nenhum factor em comum, logo vamos factorizar o 1. º membro usando um dos casos notáveis da multplicação. 3 termos Fórmula do quadrado do binómio

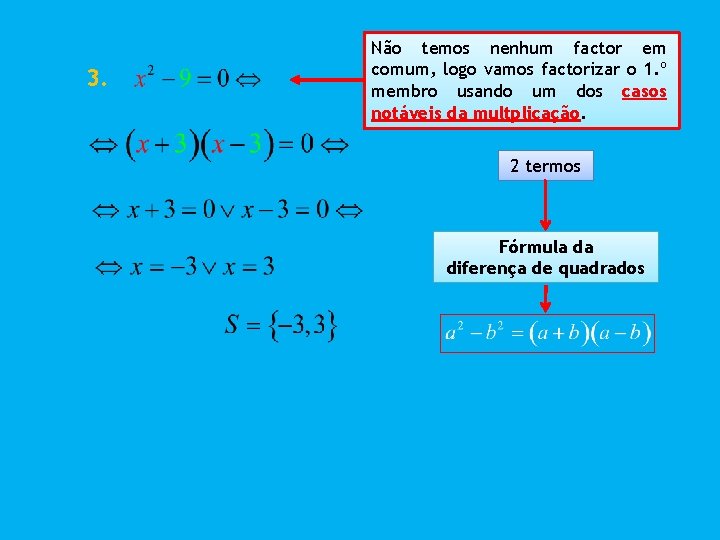
3. Não temos nenhum factor em comum, logo vamos factorizar o 1. º membro usando um dos casos notáveis da multplicação. 2 termos Fórmula da diferença de quadrados

Resolução de Equações de grau superior ao primeiro: 1. º Aplicar a Lei do Anulamento do Produto, se possível. 2. º Tiram-se os parênteses, se os houver. 3. º Tiram-se os denominadores, se os houver 4. º Passar todos os termos para o 1. º membro. 5. º Factorizar o 1. º membro. 6. º Aplicar a Lei do Anulamento do Produto. 7. º Resolver as equações. 8. º Apresentar o Conjunto Solução.

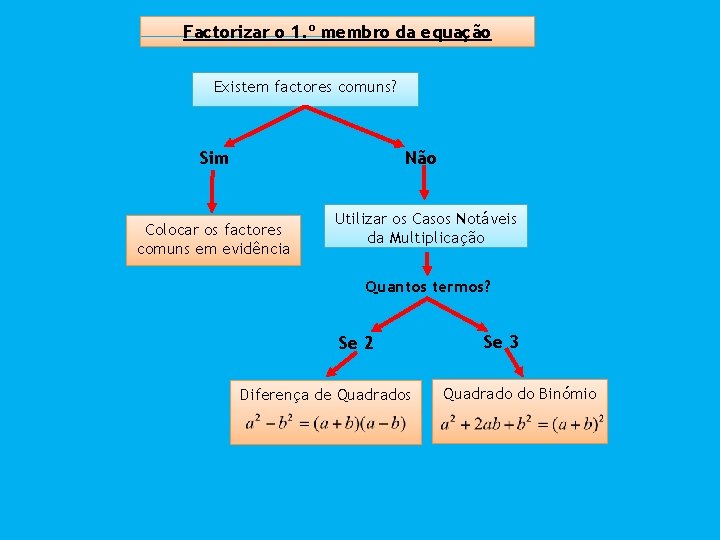
Factorizar o 1. º membro da equação Existem factores comuns? Não Sim Colocar os factores comuns em evidência Utilizar os Casos Notáveis da Multiplicação Quantos termos? Se 2 Diferença de Quadrados Se 3 Quadrado do Binómio