DERIVADAS E DIFERENCIAIS Nice Maria Americano da Costa

DERIVADAS E DIFERENCIAIS Nice Maria Americano da Costa

ACRÉSCIMO DA FUNÇÃO DEFINIÇÃO Seja uma função definida num certo intervalo, no qual, em cada ponto, a função admite um valor bem definido. Define-se o acréscimo da função, y, quando a variável independente x, sofre um acréscimo x, como a variação que a função sofre, quando se passa do ponto x para o ponto x+ x. Isto é: Exemplos:

Um dado importante para se ter idéia de quanto a função varia, quando damos um acréscimo à variável x, ou, uma medida de tal variação, é a relação entre o acréscimo da função y e o acréscimo da variável, x i. e. : A questão que se coloca então é: o que acontece com tal relação, se fizermos o acréscimo da variável x, cada vez menor? Em outras palavras, se fizermos o valor de x+x tender , cada vez mais, para x? Obviamente, estamos falando de aplicar a operação “limite” à relação. O resultado desse conjunto de operações que fizemos até aqui é o que chamamos de derivada da função.

DEFINIÇÃO DA DERIVADA A derivada da função y=f(x) é portanto o limite da relação entre o acréscimo da função e o acréscimo da variável independente x, quando este acréscimo da variável independente tende a zero. Simbolicamente, a operação derivada da função y=f(x) é designada por qualquer das seguintes notações:

Exemplo. A derivada da função

A derivada da função Note bem ! A derivada de uma função é também uma função; é uma função que, obviamente, deriva de outra pelo conjunto de operações especificadas.

A derivada da função

UM EXEMPLO CLÁSSICO A posição de um corpo em movimento é uma função do tempo, x(t). Se calculamos a derivada dessa função, temos A grandeza calculada nada mais é que a velocidade do corpo. Então, a velocidade com que se desloca o corpo é a derivada da posição em relação ao tempo.

Se agora tomamos a velocidade em função do tempo e calculamos a sua derivada, vamos achar a aceleração

INTERPRETAÇÃO DA DERIVADA f(x+ x) f 1 f f 1 A secante maior (vermelho escuro) forma o triângulo de lados f e x e com o ângulo com o eixo –x. A tangente deste ângulo vale: f(x) x 1 x x x+ x A secante menor (vermelho claro) forma o triângulo de lados f 1 e x 1 e com o ângulo 1 com o eixo –x. A tangente deste ângulo vale:

O processo de limite corresponde à aproximação do ponto x+ x do ponto x; i. e. , quando x 0. Vemos que o ângulo , no limite, tende ao ângulo e, portanto, a secante geométrica à curva tende à tangente à curva (em verde). Logo temos: A derivada da função é a tangente do ângulo que a tangente à curva faz naquele ponto. A derivada de f(x), portanto, fornece informações sobre o comportamento da função a partir da análise das tangentes à curva que representa a função. Em cada ponto x, f’(x) é igual ao coeficiente angula da reta tangente à curva de f(x) naquele ponto. Como exemplo, consideremos a f(x)=(x-2)2; uma parábola que toca o eixo-x em x=2, como mostrado na figura. Encontre as tangentes à curva, nos pontos x=1 e x=3 c

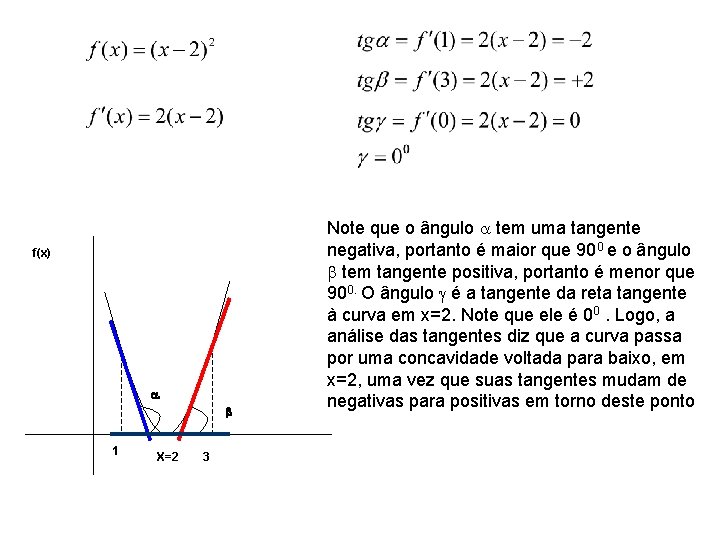
f(x) 1 X=2 3 Note que o ângulo tem uma tangente negativa, portanto é maior que 900 e o ângulo tem tangente positiva, portanto é menor que 900. O ângulo é a tangente da reta tangente à curva em x=2. Note que ele é 00. Logo, a análise das tangentes diz que a curva passa por uma concavidade voltada para baixo, em x=2, uma vez que suas tangentes mudam de negativas para positivas em torno deste ponto