Curves and surfaces 4451 3 D Modeling Graphics

Curves and surfaces 4451 3 D Modeling, Graphics, and Animation Prof. Jarek Rossignac College of Computing Georgia Institute of Technology 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 1

Lecture Objectives • Learn (by heart) the Split&Tweak and the 4 -point subdivision rules for polygons • Be able to discuss their advantages and drawbacks • Be able to design a trivial algorithm for these schemes • Understand how to construct good bounds (in 2 D and in 3 D) around the final curve from one of its approximations • Understand how to use these subdivisions to define tessellations (quads or triangles) of smooth surfaces in 3 D • Be able to design the surface subdivision schemes • Understand the benefits of having a parametric polynomial form for the curves and surfaces 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 2

Motivation • Smooth curves and surfaces are used for aesthetic, manufacturing, and analysis applications where discontinuities due to triangulated approximations would create misleading artifacts. • Designers like to specify such curves by adjusting a control polygon with only a few vertices • How to go from a crude control polygon (black) to a smooth curve (red)? • Suggestions? 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 3

Split&tweak B-spline subdivision • Given a control polygon, for example (a, b, c, d), repeat the following sequence of two steps, until all consecutive 4 -tuples of control points are nearly co-linear. 1. “Split”: insert a new control point in the middle of each edge (2, 4, 6, 8) 2. “Tweak”: move the old control points half-way towards the average of their new neighbors (1, 3, 5, 7) • The control polygon converges rapidly to a smooth curve, which happens to be a cubic B-spline curve. 2 a b 3 1 4 8 5 7 d 12/31/2021 6 c Jarek Rossignac, Co. C, GT, ©Copyright 2002 4

My first Split&Tweak in Scheme • • • • (define w 200) (define s 10) (define (draw-p-to-p p 1 p 2 col) (draw-solid-line (make-posn (+ (* (/ w s) (posn-x p 1)) w) (- w (* (/ w s) (posn-y p 1)))) (make-posn (+ (* (/ w s) (posn-x p 2)) w) (- w (* (/ w s) (posn-y p 2)))) col)) (define (draw-port col) (begin (start (* 2 w)) )) (define (last w)(cond [ (empty? (rest w)) (first w)][else (last (rest w))] )) (define (mid a b) (make-posn (/ (+ (posn-x a) (posn-x b)) 2) (/ (+ (posn-y a) (posn-y b)) 2))) (define (refine q r) (cond [(empty? (rest q)) (cons (first q) (cons (mid (first r) (first q)) empty))] [true (cons (first q) (cons (mid (first q) (first (rest q))) (refine (rest q) r))) ])) (define (subdivide q n color) (cond [(= n 0) (draws q color)] [else (subdivide (tweaks (tweakh (refine q q ))) (- n 1) color)])) (define (tweaks q) (cons (first q) (tweak (rest q)))) (define (tweak q) (cond [(or (empty? (rest q)))) q] [else (cons (first q) (cons (mid (first (rest q)) (mid (first q) (first (rest q))) ) (tweak (rest q) ))) )] )) (define (tweakh r) (cons (mid (first r) (mid (first (rest r)) (last r))) (rest r))) (define (draws q color) (draw q q color)) (define (draw q r color) (cond [(empty? (rest q)) (draw-p-to-p (first r) (last r) color) ] [else (and (draw-p-to-p (first q) (first (rest q)) color) (draw (rest q) r color) )])) (define p (list (make-posn -8 8) (make-posn 8 -8) )) (draw-port 'yellow) (draws p 'black) (subdivide p 1 'red) (subdivide p 2 'green) (subdivide p 4 'blue) 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 5

Examples from my Split&Tweak program 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 6

Yang’s version in Mat. Lab • • • function result = Sub_divide (P, color, width); [m, N] = size (P); P = [P, P(: , 1)]; % make it closed loop result = zeros (m, 2*N); even = [2: 2: 2*N]; odd = [1: 2: 2*N-1]; prev = [1: N]; next = [2: N+1]; result(: , even) = 0. 5 * (P(: , prev) + P(: , next)); • prev = [2*N, 2: 2: 2*N-2]; next = [2: 2: 2*N]; • result(: , odd) = 0. 5 * (result(: , prev) + result(: , next)); • result(: , odd) = 0. 5 * (result(: , odd) + P(: , 1: N)); 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 7

Implement your own version • • • Try for the most elegant and shortest (not the fastest) Start with an array V of n vertices of a closed polygon P in 2 D Write a procedure SHOW(V) that renders P Make another array M of n midpoints of edges of P Make a third array A, where each vertex of V is moved by 1/4 towards its neighbors in V • Display the polygons of V, M and A to verify your program • Make an array S of 2 n vertices by interleaving A and M – {A[0], M[0], A[1], M[1], A[2], M[2]…A[n], M[n]} • Display polygon of S and of V in different colors to check • Make a procedure BSPLINE(V) that takes V and returns S • SHOW(BSPLINE(BSPINE(V))))… 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 8

Inspiration • Check previous year projects with examples and sourcew code • http: //www. cc. gatech. edu/classes/AY 2003/cs 4451 b_fall/p 1 examples. htm 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 9

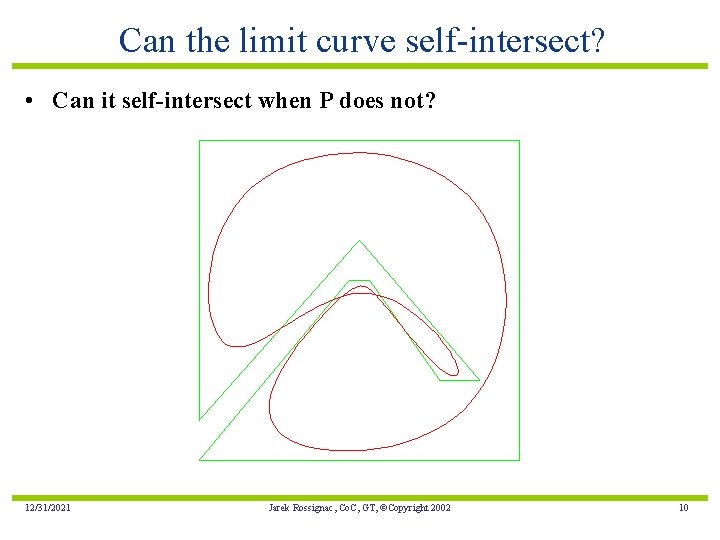
Can the limit curve self-intersect? • Can it self-intersect when P does not? 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 10

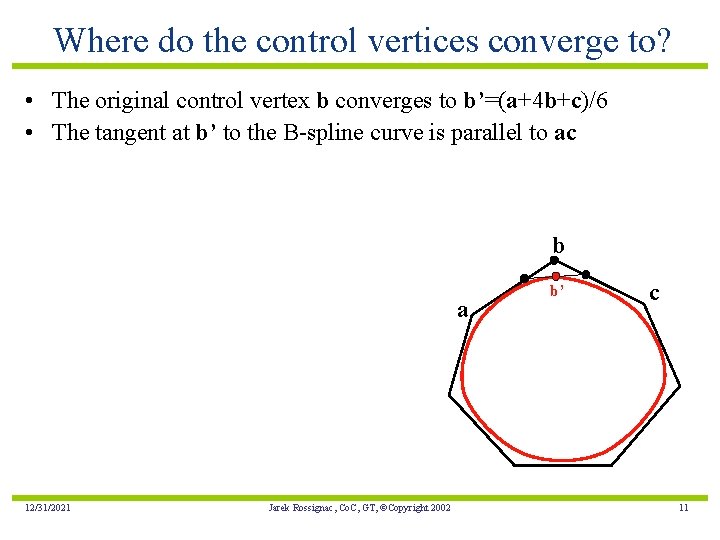
Where do the control vertices converge to? • The original control vertex b converges to b’=(a+4 b+c)/6 • The tangent at b’ to the B-spline curve is parallel to ac b a 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 b’ c 11

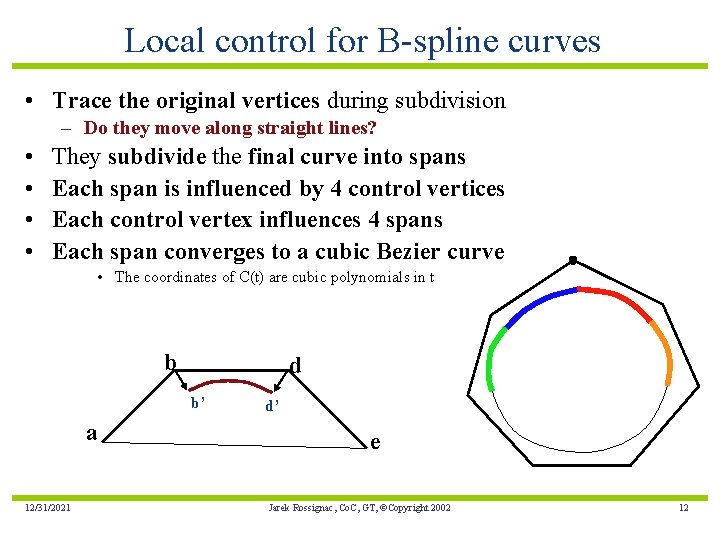
Local control for B-spline curves • Trace the original vertices during subdivision – Do they move along straight lines? • • They subdivide the final curve into spans Each span is influenced by 4 control vertices Each control vertex influences 4 spans Each span converges to a cubic Bezier curve • The coordinates of C(t) are cubic polynomials in t b d b’ a 12/31/2021 d’ e Jarek Rossignac, Co. C, GT, ©Copyright 2002 12

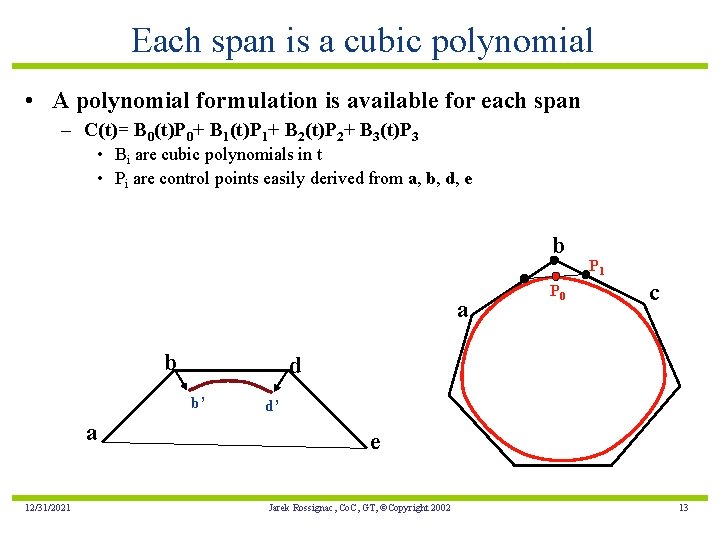
Each span is a cubic polynomial • A polynomial formulation is available for each span – C(t)= B 0(t)P 0+ B 1(t)P 1+ B 2(t)P 2+ B 3(t)P 3 • Bi are cubic polynomials in t • Pi are control points easily derived from a, b, d, e b a b 12/31/2021 c d b’ a P 0 P 1 d’ e Jarek Rossignac, Co. C, GT, ©Copyright 2002 13

Convex hull • Each span lies in the convex hull of 4 original vertices – The two from which its end-points evolved – Their immediate neighbors on each side • The convex hull of 4 points in 3 D? – A tetrahedron • The convex hull of 4 points in 2 D? – Covered by 3 triangles: ABD, ABE, BDE B D B’ A 12/31/2021 D’ E Jarek Rossignac, Co. C, GT, ©Copyright 2002 14

How can we use the convex hull property? • Display uncertainty (region guaranteed to contain the limit curve) – Shade triangles (in 2 D) or tetrahedra (in 3 D) • Decide when to stop the subdivision – All triangles or tetrahedra are nearly linear • Quickly decide when two B-spline curves in 2 D are not intersecting – The convex hulls do not overlap 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 15

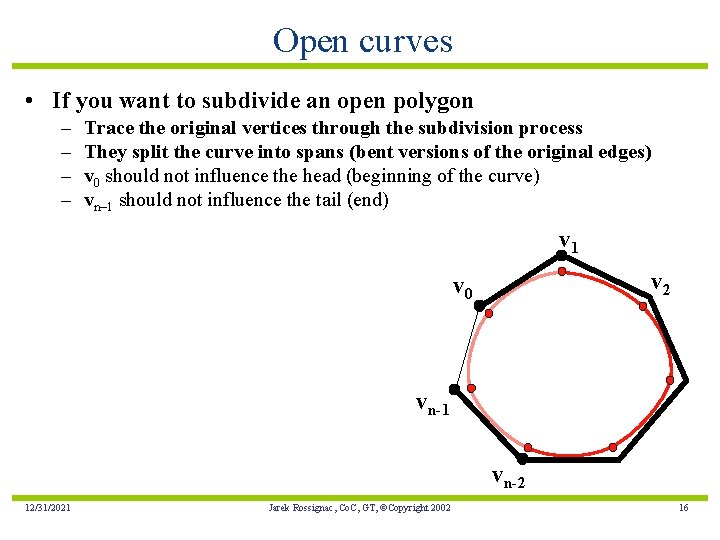
Open curves • If you want to subdivide an open polygon – – Trace the original vertices through the subdivision process They split the curve into spans (bent versions of the original edges) v 0 should not influence the head (beginning of the curve) vn– 1 should not influence the tail (end) v 1 v 2 v 0 vn-1 vn-2 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 16

4 -point subdivision • The B-spline subdivision produces a curve that does not interpolate the vertices of the original polygon P • To obtain an interpolating subdivision rule, we must leave the original vertices of P where they are, and thus must displace the mid-points. • By how much? – – – C(t)=at 3+bt 2+ct+d, and thus C(0)=d A=C(-3)=-27 a+9 b-3 c+d B=C(-1)=-a+b-c+d D=C(1)=a+b+c+d E=C(3)=27 a+9 b+3 c+d D=M+(M-M’)/8, • with 2 M=B+D and 2 M’=A+E – Offset is 1/8 of ||MM’|| 12/31/2021 C(-1) B C(-3) A Jarek Rossignac, Co. C, GT, ©Copyright 2002 C(0) M M’ C(1) D E C(3) 17

Implement your own 4 -point subdivision • Start with an array V of n vertices of a closed polygon P in 2 D • Make another array M of n midpoints of edges of P • Make a third array A, where each vertex of M is moved by 1/4 away from its neighbors in M • Display the polygons of V, M and A to verify your program • Make an array S of 2 n vertices by interleaving V and A – {V[0], A[0], V[1], A[1], …V[n], A[n]} • Display polygon of S and of V in different colors to check. • Make a procedure FOURPTS(V) that takes V and returns S • SHOW(FOURPTS(FOURPTS(V))))… 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 18

Compare both approaches • Which one interpolates the original vertices? • Which one produces the smoothest curve? – When is this important? • Can both have cusps (non smooth points)? • How can you force the B-spline curve to go through a point? • Which one has a convex-hull property? – When is this important? 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 19

Cubic B-spline and four-points • From James Koch 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 20

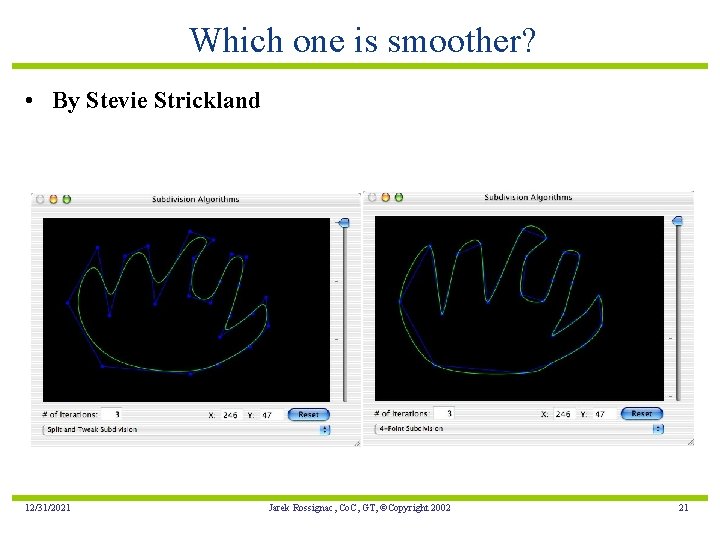
Which one is smoother? • By Stevie Strickland 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 21

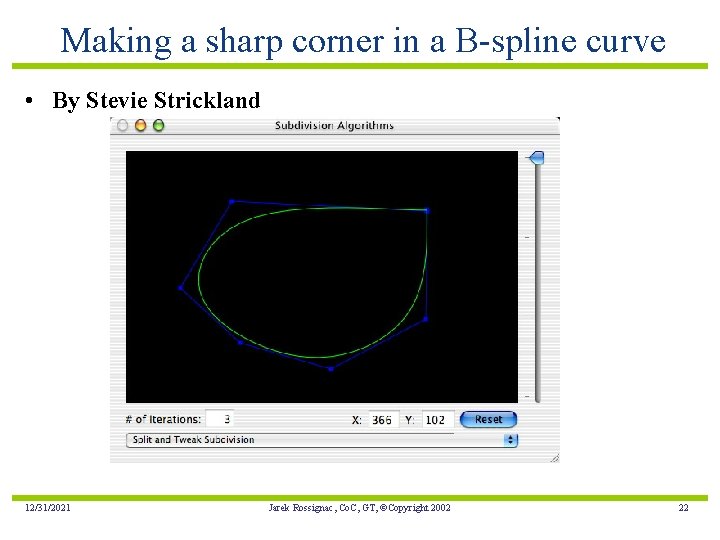
Making a sharp corner in a B-spline curve • By Stevie Strickland 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 22

A compromise • B-spline subdivision rounds the corners and thus shrinks a convex shape • 4 -points subdivision bulges the edges out and hence grows a convex shape • Both produce curves that are relatively far from the initial control polygon • We may want a compromise – Closer to the polygon – Bulging less – Cuttling less 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 23

Jarek’s subdivision • Split each edge as before (in both schemes) • Tweak old vertices by half of the B-spline displacement and the new vertices by half of the 4 -point displacement 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 24

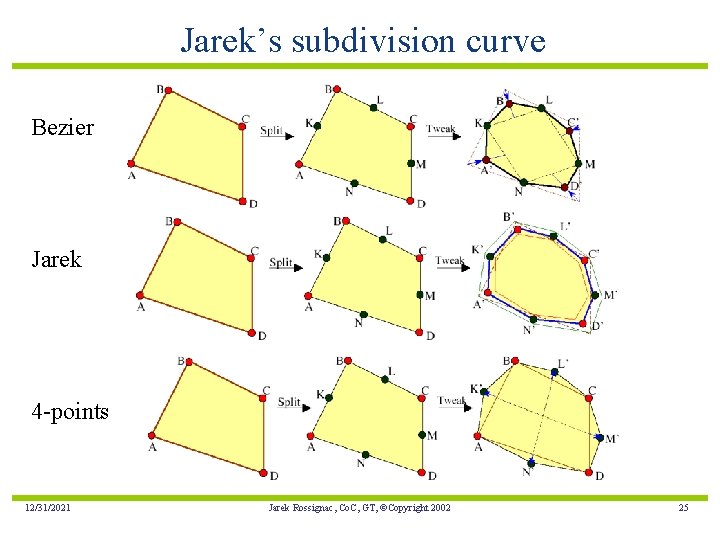
Jarek’s subdivision curve Bezier Jarek 4 -points 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 25

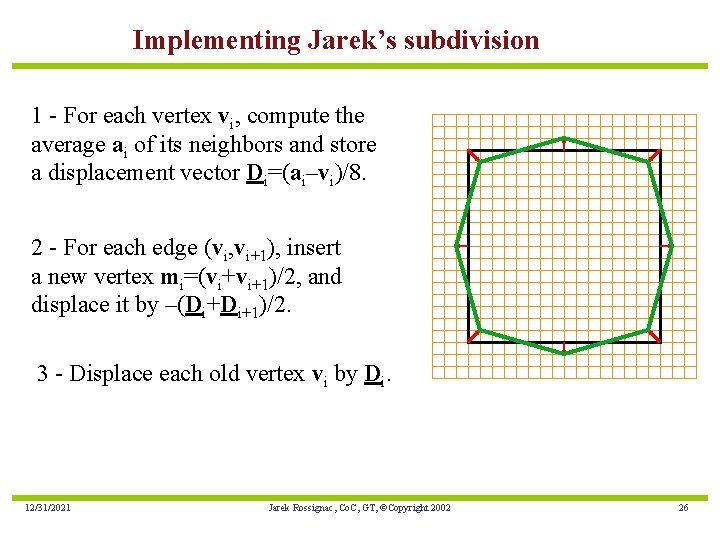
Implementing Jarek’s subdivision 1 - For each vertex vi, compute the average ai of its neighbors and store a displacement vector Di=(ai–vi)/8. 2 - For each edge (vi, vi+1), insert a new vertex mi=(vi+vi+1)/2, and displace it by –(Di+Di+1)/2. 3 - Displace each old vertex vi by Di. 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 26

Three subdivision schemes • B-spline (uniform cubic B-spline), most popular: – Introduces new vertices at edge mid-points (split) – Tucks in the old vertices by 1/2 the displacement towards the average of their new neighbors (tweak) – Very smooth result: piecewise cubic parametric formulation – Does not interpolate the original vertices – Shrinks convex regions • 4 -points: – Leaves the old vertices unchanged – Bulges the edges by displacing their mid-point away from the average of the neighbors (split & tweak) – Interpolates the original vertices – Grows convex regions • Jarek – Combines half of the tweaks of the other two – Final curve is closer to the original polygon 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 27

What about curves in 3 D? • Nothing was said about the dimension of the space. • The procedures work for any dimension and in any space. • You can apply the subdivision to the x coordinates first, then to the y coordinates, then to the z, or to the 3 D points. 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 28

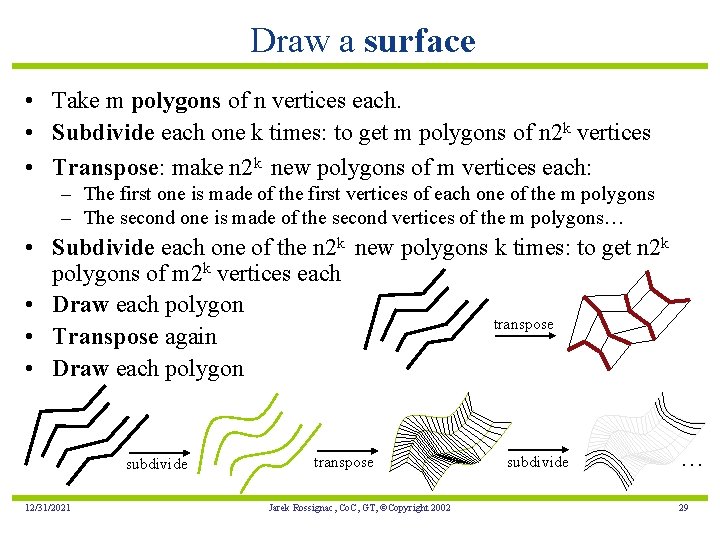
Draw a surface • Take m polygons of n vertices each. • Subdivide each one k times: to get m polygons of n 2 k vertices • Transpose: make n 2 k new polygons of m vertices each: – The first one is made of the first vertices of each one of the m polygons – The second one is made of the second vertices of the m polygons… • Subdivide each one of the n 2 k new polygons k times: to get n 2 k polygons of m 2 k vertices each • Draw each polygon transpose • Transpose again • Draw each polygon subdivide 12/31/2021 transpose Jarek Rossignac, Co. C, GT, ©Copyright 2002 subdivide … 29

Example of a B-spine subdivision • By James Koch (notice that the surface does not even go through the control loops 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 30

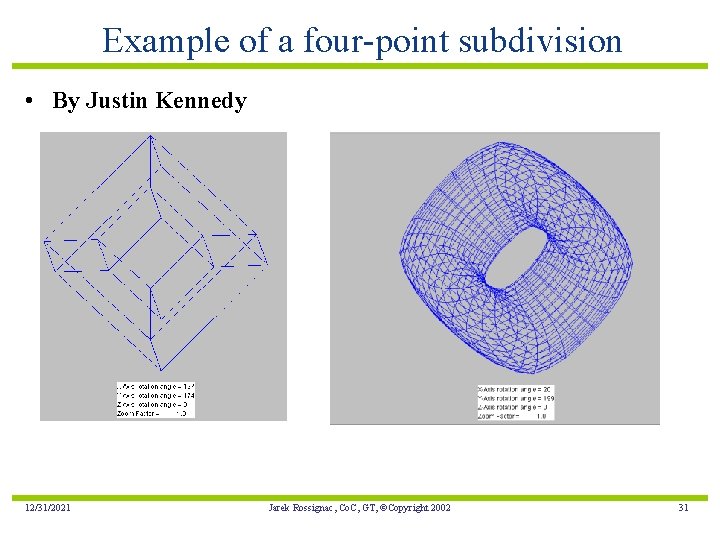
Example of a four-point subdivision • By Justin Kennedy 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 31

Example of a mixed subdivision • By Jesse Shieh 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 32

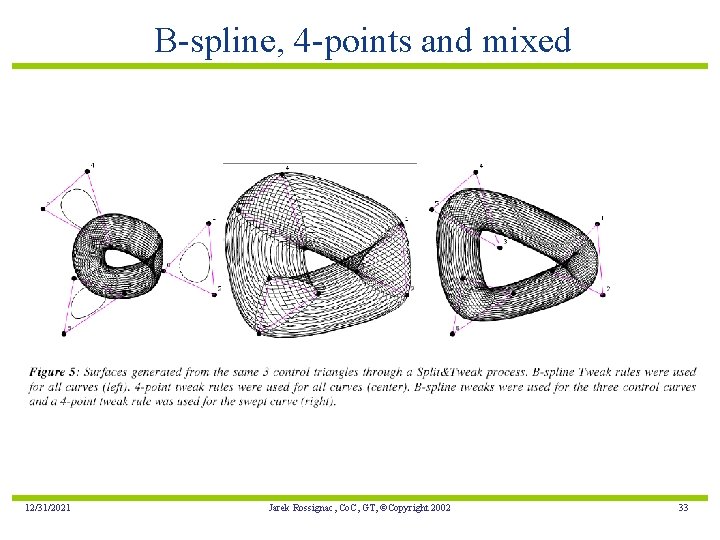
B-spline, 4 -points and mixed 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 33

How to produce a tessellation of the surface • Perform the subdivide-transpose-subdivide-transpose • Capture all quads, each bounded by four edge produced by the previous process. • Display them as quads or triangulate each one 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 34

Four-point torus from 3 triangles • By Ignacio Llamas 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 35

More complex torus with normals • By Peter Presti 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 36

What you must remember • • Names and subdivision rules for all 3 schemes How to implement them How to compute the convex hull for B-spline spans How to generate 3 D surfaces by using these schemes 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 37

Examples of simple questions for quiz • • Name three curve subdivision schemes discussed in class? What are the two steps of the cubic B-spline subdivision? Does a B-spline subdivision interpolate the original vertices? What is the difference between the implementations of the Bspline and the 4 -point subdivision schemes? What is a span in a polygon produced by B-spline subdivision. Provide a formulation of a pointset that contains such a span. Provide a detailed pseudocode for Jarek’s subdivision scheme. Explain how you can use the curve subdivision to produce surfaces. 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 38

Research questions to think about • Jarek’s subdivision is a 50/50 compromise between the Bspline and the 4 -point schemes. How would you implement a t/(1 -t) compromise? • Design a simple algorithm that would implement any of the split&tweak subdivisions step in a single pass over the vertices. (You may keep a small buffer of the last few vertices, but assume no random access. ) • Suppose that you move a single vertex of the original control polygon. How many spans of the final curve are affected? Is the answer the same for all three subdivision schemes? • Are these two formulations of Jarek’s subdivision equivalent? – Tweak old vertices by half of the B-spline displacement and the new vertices by half of the 4 -point displacement – For each vertex vi, compute the average ai of its neighbors and store a displacement vector Di=(ai–vi)/8. Then, for each edge (vi, vi+1), insert a new vertex mi=(vi+vi+1)/2, and displace it by –(Di+Di+1)/2. Finally, displace each old vertex vi by Di. 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 39

Project 1 In pairs. Design & program together! Report individually. • January 13: Phase 1 A (making and drawing polygons) – Create/draw/save polygons in 2 D using Open. GL • January 20: Phase 1 B (split&tweak subdivision) – Implement a weighted average of B-spline and 4 -points • January 27: Phase 1 C (Studies span of control, area change) – See how much of the curve is affected by moving one vertex – Compute change in area change between the original and the three subdivision curves • February 3: Phase 1 D (simplification and error measure) – Explore different criteria for deleting vertices in simplification – Measure the resulting error Start with previous year projects (source code and discussions): http: //www. cc. gatech. edu/classes/AY 2003/cs 4451 b_fall/p 1 examples. htm Most of the grade is in the report, not the code! Plan your work: sequence, testing, figures 12/31/2021 Jarek Rossignac, Co. C, GT, ©Copyright 2002 40